- 1java中String类详解(java.lang.String)
- 2计算机安全中心无法启动,win10无法启动安全中心服务的解决方法
- 3专利转化运用行动方案解读-于春堂|中国智库·国家(中国)智库
- 4activity中Variable和VariableLocal在taskService和runtimeService中的设置和获取_taskservice.getvariables
- 5微信小程序使用蓝牙连接硬件_startbluetoothdevicesdiscovery
- 6循环神经网络:GRU_gru神经网络谁发明的
- 7C++ 链表有环问题解决_链表有环怎么处理
- 8pnpm配置(重启!重启!重启!)_pnpm环境变量设置
- 92020年十大IC设计企业_ic设计企业排名
- 10IOS 使用itms-services协议,服务端安装应用
机器学习(一)- 线性回归/(拟合)模型_线性拟合求均值的方法
赞
踩
# 前年学习记录的笔记,分享一下~
Linear Models for Regression
目录
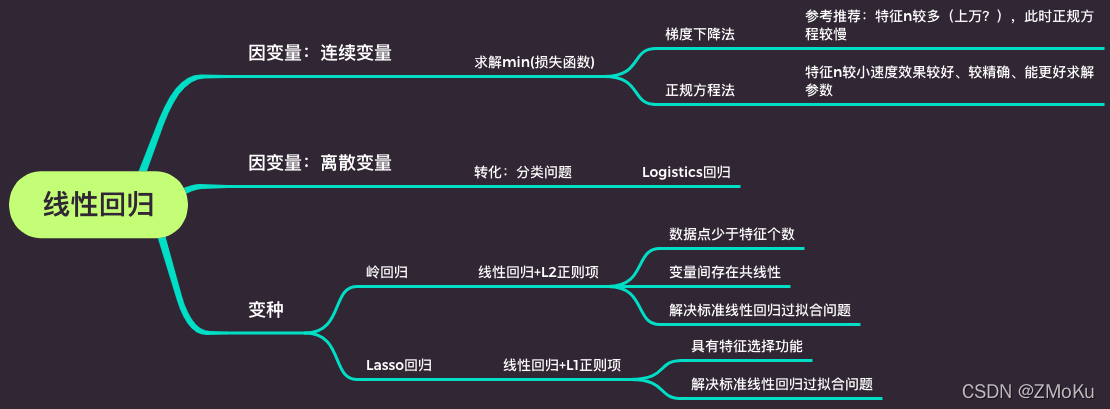
二、线性回归,针对线性数据,通过最小二乘法让损失函数(cost function)最小,求得方程系数,得到方程。
三、多元线性回归求解cost function:正规方程法和梯度下降法
一、使用线性回归模型前数据处理及注意


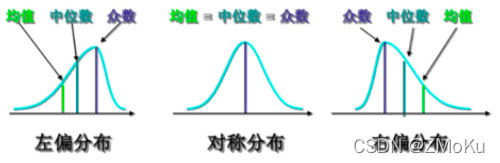
二、线性回归,针对线性数据,通过最小二乘法让损失函数(cost function)最小,求得方程系数,得到方程。
线性回归函数:
![]()
损失函数(最小二乘):损失越小,h(x)越接近y(x),即拟合值越接近真实值。
![]()
回归系数(权重)不可知,需要不断调整,使损失函数尽可能少。
依据:梯度下降法
梯度:即函数的导数
此时损失函数寻找的是最小值,即梯度的负方向探寻回归系数,该算法称为梯度”下降“法

梯度下降算法-步骤

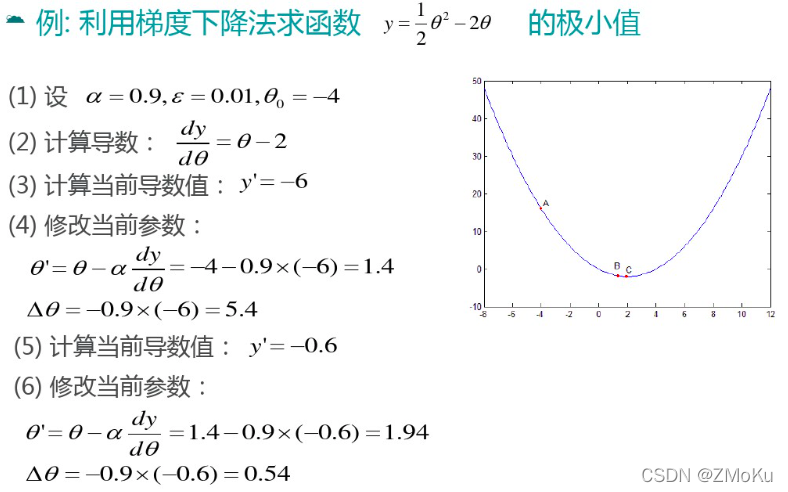
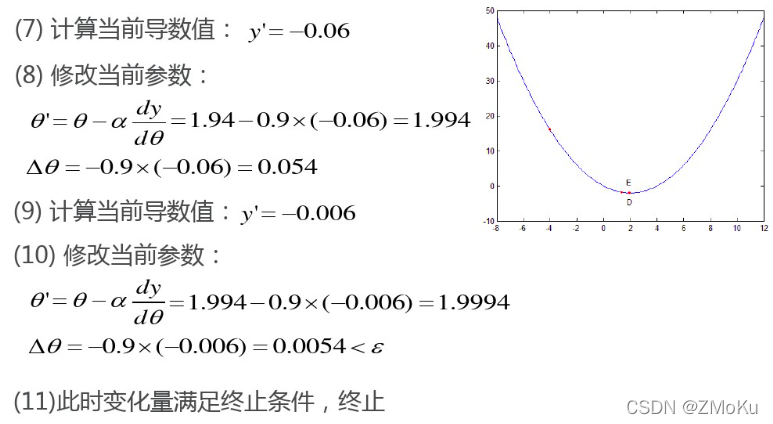
同理,求损失函数J的最小值:

应用到不止一个训练实例的情况:
![]()
批量梯度下降算法:每次更新系数参数都要考虑整个训练集。【线性模型较简单,训练时间优先级不高,推荐使用】
随机梯度下降算法:一次仅用一个样本来更新系数。
线性最小二乘问题的矩阵解法。
最小二乘的概率解释:最小二乘回归相当于寻找最大似然函数的参数值。
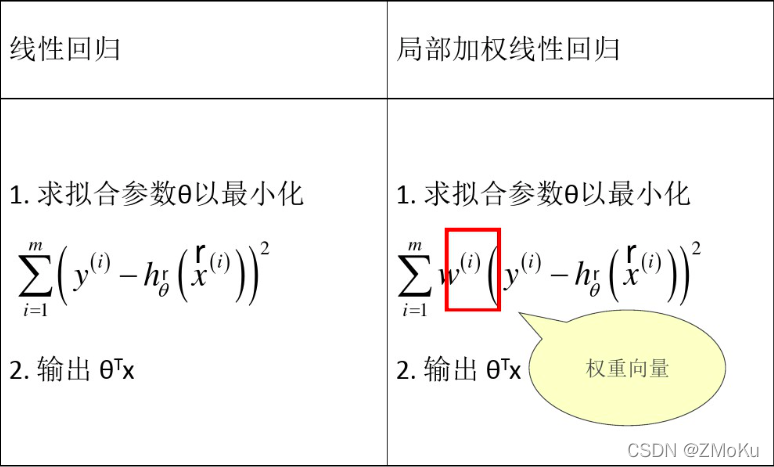
局部加权线性回归:
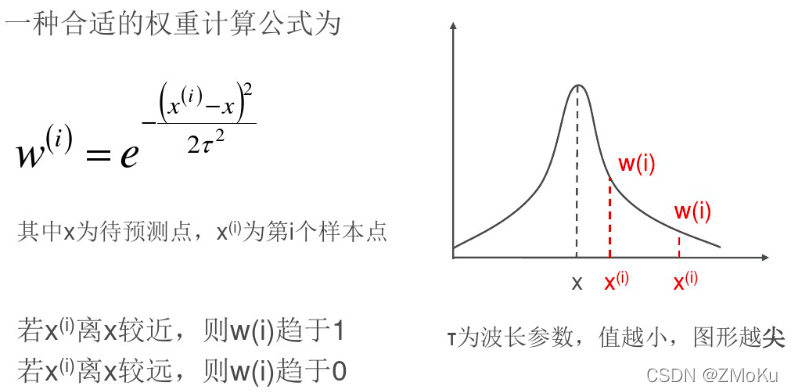
给每个训练样本赋予一个权重w,越靠近待预测点的训练样本,对预测结果的影响越大,训练样本离预测点越近,w趋于1;越远离待预测点的训练样本,对预测结果的影响越小,训练样本离预测点越远,w趋于0。
直观理解:局部加权线性回归在给定预测点时,对其附近的点进行训练得到局部线性模型,并用于预测。

三、多元线性回归求解cost function:正规方程法和梯度下降法
正规方程法(最小二乘):
![]()
多元线性回归:![]()
矩阵形式: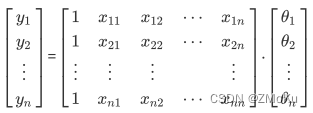
对矩阵求偏导:[ OS: RSS,数学名词,是数和的平方根]

由此得到参数的解,但其中的逆矩阵不一定存在解,即可能存在多重共线性(特征间线性相关程度很大),因此加入L1,L2正则化来进行控制。
梯度下降法:
判别函数:![]()
cost function:![]() ,1/m即求均值。
,1/m即求均值。
梯度下降法:![]()
得,![]()
【详细了解可参考:梯度下降算法详解】
四、标准线性回归的延伸:岭回归和Lasso回归
-
解决特征数量比样本量多的问题
-
作为降维算法可以判断哪些特征重要哪些不重要,类似于降维的效果。
-
缩减算法可以看作是对一个模型增加偏差的同时减少方差。
-
数据点少于变量个数
-
变量间存在共线性(最小二乘回归得到的系数不稳定,方差大)
五、梯度下降法的优化。
-
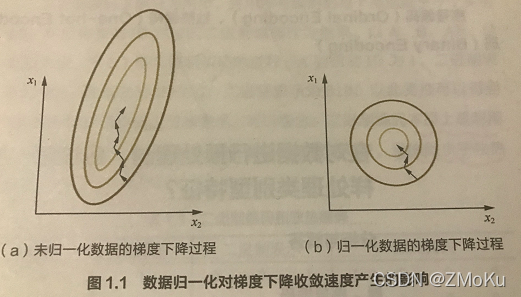
特征缩放
-
学习速率的选取可考虑:0.01 -> 0.03 -> 0.1 -> 0.3 -> 1 -> 3(重复alpha1=alpha0*3; alpha2=alpha1/3*10)
六、线性回归中可能遇到的问题及解决办法
如果学习速率选取过小,会导致迭代次数变多,收敛速度变慢;学习速率选取过大,有可能跳过最优解,最终导致根本无法收敛。
在计算时要同时更新,使用梯度下降法容易得到局部最优解,要尝试不同的学习速率,然后找到最好的那个。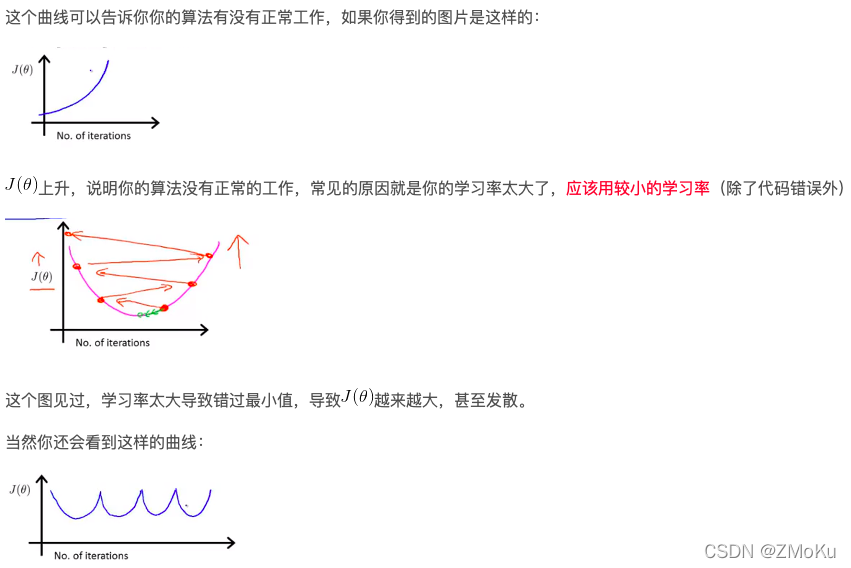
1、采用固定的学习速率,会存在上面问题。
2、采用变换的学习速率,也就是当梯度大时,学习速率也大,当梯度小时,学习速率也小。学习速率采用与梯度正相关关系,存在一个比例系数,采用固定的这个比例系数。得到的结果是,
采用这个算法对上面的问题有一定的缓解作用,但有时解决也不是很好。

[OS:参考:梯度下降法中的参数学习速率如何选择_zrh_CSDN的博客-CSDN博客]
3、采用变换的学习速率还是会存在上述问题,所以后面很多算法采用比例系数也变化的方法。
4、设置0.1或0.1附近时效果一般不会太差。
问题3:过拟合
解决方法:1、丢弃一些对最终预测结果影响不大的特征,可采用PCA算法实现。
2、使用正则化技术,保留所有特征,减少特征前面的参数theta的大小,即修改cost function形式(Ridge Regression、Lasso Regression)
七、拓展:偏差与方差
参考:岭回归和Lasso回归_Joker_sir5的博客-CSDN博客_岭回归和lasso回归
模型误差 = 偏差(Bias) + 方差(Variance) + 数据本身的误差(无法避免)
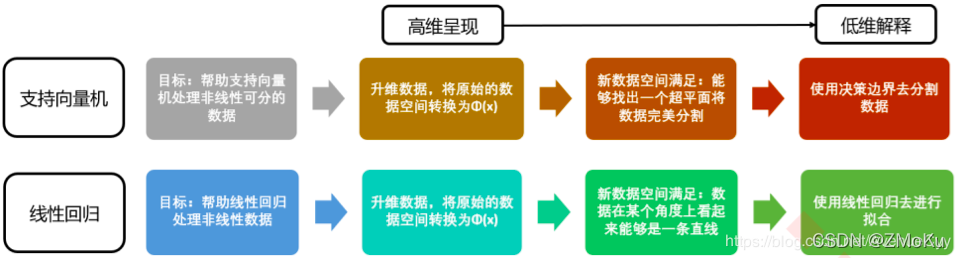
偏差:导致偏差的原因有很多种。其中一个就是针对非线性问题采用线性方法求解,当模型欠拟合时,就会出现较大偏差。
方差:产生高方差的原因通常是由于模型过于复杂,即模型过拟合,会出现较大的方差。
通常情况下,我们降低了偏差相应地会使方差提高,降低方差就会相应地提高偏差。
还有一种对岭回归和Lasso回归折中的方法——弹性网络(Elastic net)
![]()


