【数据结构】——堆

目录

1：堆的概念及结构

1）：概念：

2：堆的实现 

1）：向下调整算法

 2）：堆的初始化和销毁

3）： 堆的插入

一）：向上调整

4）：交换节点

 5）：堆的删除

1）： 向下调整

6）：取堆顶数据

7）：判空

3：总代码 

---

1：堆的概念及结构

1）：概念：

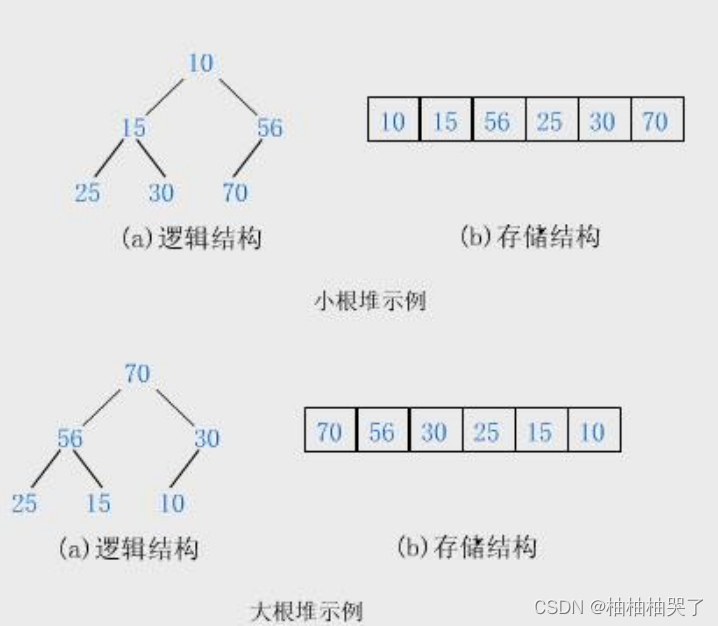
2：堆的实现 

1）：向下调整算法

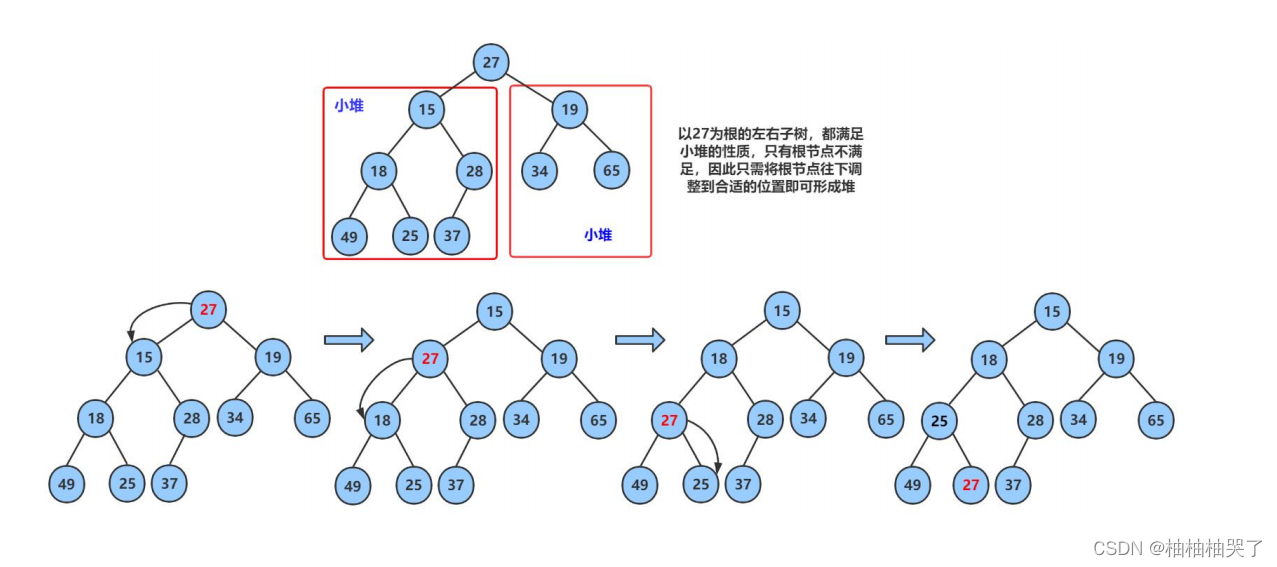
 2）：堆的初始化和销毁

1：对堆进行初始化，因为堆的底层是数组，所以我们也就相当于是对数组进行初始化，将数组（a）初始为NULL、将有效数据个数（size）以及空间大小（capacity）都初始化为0；

2：销毁时，先将数组（a）释放（free），然后需要手动将数组a置为NULL，再将有效数据个数（size）以及空间大小（capacity）都置为0；

//初始化
void HPInit(HP* php)
{
	assert(php);
 
	php->a = NULL;
	php->size = php->capacity = 0;
}
 
//销毁
void HPDestory(HP* php)
{
	assert(php);
 
	free(php->a);
	php->a = NULL;
	php->size = php->capacity = 0;
}

3）： 堆的插入

插入数据要从倒数第一个叶子节点的后面开始插入，然后再向上进行调整

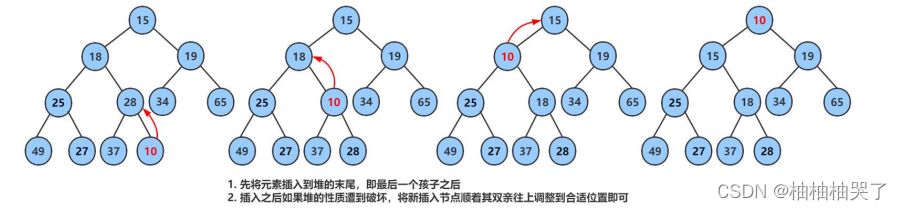
1：因为这里是数组，所以在插入前我们需要先判断一下要插入的空间是否足够，如果不够需要进行扩容，如果扩容失败，就直接返回一个非0值就好（正常退出返回0，异常退出返回非0），然后在php->a[php->size]处插入我们需要插入的值x，再让php->size++就好 

2：最后我们需要对堆进行向上调整（AdjustUp），因为这里我们计算的是下标，因此size是指向最后一个数的下一个位置处，我们这里让size-1就取到了最后一个数

//插入
void HPPush(HP* php, HPDatatype x)
{
	assert(php);
 
	if (php->size == php->capacity)
	{
		int newcapacity = php->capacity = 0 ? 4 : php->capacity * 2;
		HPDatatype* tmp = (HPDatatype*)realloc(php->a, php->capacity * sizeof(HPDatatype));
		if (tmp == NULL)
		{
			perror("realloc fail");
			return;
		}
		php->capacity = newcapacity;
		php->a = tmp;
	}
	php->a[php->size] = x;
	php->size++;
 
	//szie - 1  这里是下标，所以sizeo要减一
	AdjustUp(php->a, php->size - 1);
}

一）：向上调整

1：我们先算出父亲节点（parent），这里是=让（child - 1）/ 2 就可以计算出父亲节点（parent），算好后创建一个循环，当child > 0 时停止循环，因为这里是向上调整，当child 调整到根节点（下标为0）处就不需要再调整了

2：我们这里是向上调整建小堆，所以当child 小于 parent 时，满足小堆孩子小于父亲的条件，就交换child  和 parent 的位置，将parent 给给 child，这里新的parent 还有父亲节点，他也就是其父亲节点的子（孩子）节点，所以我们需要再算出他的父亲节点

3：如果child 大于 parent ,那么不满足我们这里建小堆的条件，则直接break

//向下调整
void AdjustUp(HPDatatype* a, int child)
{
	//算父亲
	int parent = (child - 1) / 2;
 
	//while(parent >= 0)
	while (child > 0)
	{
		//孩子小于父亲  
		if (a[child] < a[parent])//小堆
		{
			//交换孩子和父亲
			Swap(&a[child], &a[parent]);
			child = parent;
			//重新算child的parent
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

4）：交换节点

交换child 和 parent 的位置

1：有的人会问这里交换节点传值时我们为什么不传结构体指针，而是传整形，这是因为这里传整形可以方便我们在直接建堆

2：交换时我们先用tmp存一下p1，然后让p1和p2进行交换，再把tmp的值给给p2 

//交换
void Swap(HPDatatype* p1, HPDatatype* p2)
{
	HPDatatype* tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

 5）：堆的删除

删除时，将堆顶的数据和最后一个叶子节点进行交换，然后再向下进行调整

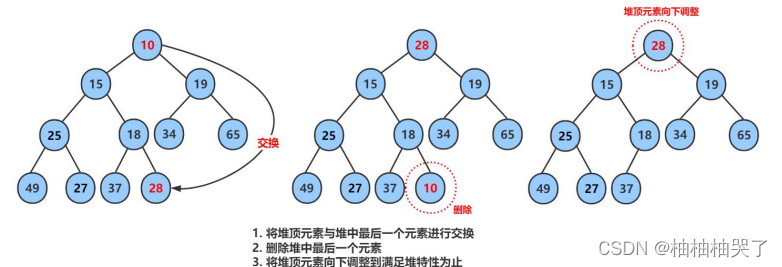
1：删除时我们是删除堆顶的数据，但是堆顶的数据在数组中删除时需要我们挪动数据，把数据从后向前挪动，数据的挪动会改变节点之间的兄弟关系，让兄弟节点变为父子节点，所以我们这里需要用到一种特殊的办法，让根节点根最后一个叶子进行交换，然后再对堆进行向下调整算法

//删除
void HPPop(HP* php)
{
	assert(php);
	assert(php->size > 0);
 
	Swap(&php->a[0], &php->a[php->size - 1]);
	php->size--;
 
	AdjustDown(php->a, php->size, 0);
}

1）： 向下调整

1：用假设法，假设左孩子（child）小（默认child是左孩子），然后计算出父亲节点（parent）的左孩子的下标，计算方法：parent * 2 + 1，父亲节点乘2，再加1就是child的下标

2：接下来我们要找出左孩子和右孩子哪个孩子小，while循环的结束条件是，当child  < n（size）时循环停止，因为数组a的末尾是叶子，如果child等于数组末尾，就说明没有孩子了，没有孩子了就不能进行向下调整

3：因为前面我们用的是假设法，当我们假设错误，右孩子（child+1）< 左孩子（child），就++child，因为堆的本质是数组，++以后就让child就指向数组中的下一个数，在堆当中就相当于++到了左孩子的兄弟节点处（右孩子child+1处），然后从child+1（右孩子）处向下进行调整，

并且child+1（右孩子）还需要 < n（size），如果child+1 > n，就说明child+1超出了数组 

4：当child < parent ，建小堆的条件成立，开始进行调整，对parent 和 child 进行交换，再将child给给parent，最后再计算出parent 的child（孩子），如果child > parent，那么条件不成立，则直接退出

//向下调整
void AdjustDown(HPDatatype* a, int n, int parent)
{
	//假设法
	//假设左孩子小（默认child是左孩子）
	int child = parent * 2 + 1;
 
	//n（size） 数组a下标的数组末尾是叶子，如果child等于数组末尾，就说明没有孩子了
	//找出小的那个孩子
	while (child < n) //在数组中如果child >= n 说明孩子不存在 ，调整到叶子了，叶子节点没有子节点（没有孩子child）  
	{
		//右孩子（child+1）如果右孩子小于左孩子
		if (child + 1 < n && a[child + 1] < a[child])
		{
			//就从右孩子（child+1）那里向下调整
			//本质是数组，++以后让child就指向下一个数，在堆当中就相当于++到了左孩子的兄弟节点处（右孩子child+1处）
			++child;
		}
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

6）：取堆顶数据

1：数组中下标为0的数就是堆顶数据，所以直接返回a[0]

//取堆顶数据
HPDatatype HPTop(HP* php)
{
	assert(php);
	assert(php->size > 0);
 
	//返回堆顶的数据
	return php->a[0];
}

7）：判空

1：有效数据个数size不为0那么堆就不为空

//判空
bool HPEmpty(HP* php)
{
	assert(php);
 
	return php->size == 0;
}

3：总代码 

//初始化
void HPInit(HP* php)
{
	assert(php);
 
	php->a = NULL;
	php->size = php->capacity = 0;
}
 
//销毁
void HPDestory(HP* php)
{
	assert(php);
 
	free(php->a);
	php->a = NULL;
	php->size = php->capacity = 0;
}
 
//交换
void Swap(HPDatatype* p1, HPDatatype* p2)
{
	HPDatatype* tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}
 
//向上调整
void AdjustUp(HPDatatype* a, int child)
{
	//算父亲
	int parent = (child - 1) / 2;
 
	//while(parent >= 0)
	while (child > 0)
	{
		//孩子小于父亲  
		if (a[child] < a[parent])//小堆
		{
			//交换孩子和父亲
			Swap(&a[child], &a[parent]);
			child = parent;
			//重新算child的parent
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}
 
//插入
void HPPush(HP* php, HPDatatype x)
{
	assert(php);
 
	if (php->size == php->capacity)
	{
		int newcapacity = php->capacity = 0 ? 4 : php->capacity * 2;
		HPDatatype* tmp = (HPDatatype*)realloc(php->a, php->capacity * sizeof(HPDatatype));
		if (tmp == NULL)
		{
			perror("realloc fail");
			return;
		}
		php->capacity = newcapacity;
		php->a = tmp;
	}
	php->a[php->size] = x;
	php->size++;
 
	//szie - 1  这里是下标，所以sizeo要减一
	AdjustUp(php->a, php->size - 1);
}
 
//向下调整
void AdjustDown(HPDatatype* a, int n, int parent)
{
	//假设法
	//假设左孩子小（默认child是左孩子）
	int child = parent * 2 + 1;
 
	//n（size） 数组a下标的数组末尾是叶子，如果child等于数组末尾，就说明没有孩子了
	//找出小的那个孩子
	while (child < n) //在数组中如果child >= n 说明孩子不存在 ，调整到叶子了，叶子节点没有子节点（没有孩子child）  
	{
		//右孩子（child+1）如果右孩子小于左孩子
		if (child + 1 < n && a[child + 1] < a[child])
		{
			//就从右孩子（child+1）那里向下调整
			//本质是数组，++以后让child就指向下一个数，在堆当中就相当于++到了左孩子的兄弟节点处（右孩子child+1处）
			++child;
		}
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
 
//删除
void HPPop(HP* php)
{
	assert(php);
	assert(php->size > 0);
 
	Swap(&php->a[0], &php->a[php->size - 1]);
	php->size--;
 
	AdjustDown(php->a, php->size, 0);
}
 
//取堆顶数据
HPDatatype HPTop(HP* php)
{
	assert(php);
	assert(php->size > 0);
 
	//返回堆顶的数据
	return php->a[0];
}
 
//判空
bool HPEmpty(HP* php)
{
	assert(php);
 
	return php->size == 0;
}

 以上就是堆的所有实现了，创作不易，求求大家点个小赞赞，感谢各位老们的赏脸观看，随手点个赞，养成好习惯，如有问题，感谢反馈！