【数据结构初阶-排序】经典的排序算法，很有趣，有没有你不会的呢_数据结构排序的趣味题

前言

本期分享经典排序：

• 插入排序
  • 直接插入排序
  • 希尔排序
• 选择排序
  • 直接选择排序
  • 堆排序
• 交换排序
  • 冒泡排序
  • 快速排序
• 归并排序
• 非比较排序
  • 计数排序

注：讲解时默认排升序

插入排序

直接插入排序

思想

插入排序，就像玩扑克时，摸牌的过程：

• 最开始，左手没牌，右手从牌堆中摸
• 右手每次摸进一张牌，都从右到左比较，找到位置插入新牌
• 如此一来就能保证左手的排始终有序，摸完牌后也就排序完成

操作

• 设begin为已排序序列 arr1 的左闭区间，end为 arr1 的右闭区间，则有 arr1 的左闭右闭区间 [begin, end]
• 单趟排序：
  • 每次保存起未排序序列 arr2 的元素 arr[end+1] 为 tmp，从右到左和 arr1 的元素比较
    • 是正确位置：插入
    • 不是正确位置：arr[end] 往后挪，tmp接着从右到左和 arr1 的元素比较
• 整体趟数：
  • 若元素个数为n，需要排n趟

void InsertSort(int* arr, int sz)
{
	//end + 1 < sz
	//end < sz - 1
	int i = 0;
	for (i = 0; i < sz - 1; i++)
	{
		int end = i;
		int tmp = arr[end + 1];

		//找插入位置
		while (end >= 0)
		{
			//不是插入位置：当前数据往后挪
			if (tmp < arr[end])
			{
				arr[end + 1] = arr[end];
				end--;
			}
			//是插入位置：跳出循环插入
			else
			{
				break;
			}
		}
		//插入
		//1. 插入位置是[0]，end == -1，不合循环条件跳出
		//2. 找到插入位置，break跳出
		arr[end + 1] = tmp;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

稳定性

插入排序中元素都是单一向右挪动，相等的元素不会改变相对顺序，所以

直接插入排序是稳定的

复杂度

时间复杂度

最好：当前元素只需要和前一个比较一下，这时需要比n-1次（最后一个天然有序）

O(n)

最坏：逆序，比较次数：1+2+3+……+n-1 次，为等差数列，数量级为n^2

O(n^2)

空间复杂度

O(1)

希尔排序（缩小增量排序）

希尔排序是直接插入排序的优化版本：按不同步长对元素进行分组，再进行插入排序

优化思想

增量gap不止用来分组，也意味着数据移动的步长，所以

1. gap很大时，序列很无序，插入排序的元素少，移动快
2. gap不断变小，序列有序多了，插入排序的元素多，但插入排序对相对有序的序列效率高

操作

• 单趟排序：

  • 设定一个不断减小的增量gap，也是元素移动的步长
  • 以gap对序列分组，并对每组分好的序列进行直接插入排序
  • 不断缩小gap，并排序
  • *gap>1 时，进行的是预处理排序，gap == 1时进行的是直接插入排序

• 整体趟数：

  • 由gap决定：当gap = 1，排序完成

注：增量亦称改变量，指的是在一段时间内，自变量取不同的值所对应的函数值之差。这里指自变量取不同的值，不同分组间排序的差别。

void ShellSort(int* arr, int sz)
{
	int gap = sz;
	
    //gap > 1，预处理排序
    //gap == 1，直接插入排序
	while (gap > 1)
	{
		gap = gap / 3 + 1;//保证最后一次gap==1，进行直接插入排序
		//gap组
		for (int j = 0; j < gap; j++)
		{
            //end + gap < sz
			//end < sz - gap
			for (int i = j; i < sz - gap; i += gap)//每次跳gap步
			{
				int end = i;
				int tmp = arr[end + gap];
				while (end >= 0)
				{
					if (tmp < arr[end])
					{
						arr[end + gap] = arr[end];
						end -= gap;
					}
					else
					{
						break;
					}
				}
				arr[end + gap] = tmp;
			}
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

其实就是套上”缩小增量“的直接插入排序

稳定性

我们知道一次插入排序是稳定的，不会改变相同元素的相对顺序，但在多次不同的插入排序过程中，相同的元素可能在各自的插入排序中移动，最后其稳定性就会被打乱，所以

希尔排序是不稳定的

复杂度

时间复杂度

希尔排序的时间复杂度随增量的变化而变化，难以计算，根据某位前辈大量实验数据能大概估算：

O(n^1.3)

空间复杂度

O(1)

选择排序

直接选择排序

思想

选择排序，遍历序列，选出最小的元素，交换到左边

优化版本：

每次选出最小元素交换到左边，选出最大元素交换到右边

操作

• 设 begin 为待排序序列 arr 的左闭区间，end为 arr 的右闭区间，则有 arr 的左闭右闭区间 [begin, end]

  设 mini 为单趟遍历中最小元素的下标，maxi 为单趟遍历中最大元素下标

• 单趟排序：

  • 遍历选最值的下标
  • 交换 arr[begin] 和 arr[mini] 、arr[end] 和 arr[maxi]
  • （修正）

• 整体趟数

  • 若元素个数为n，趟数为 (2/n)

修正：交换最值到其位置时有先后顺序，如果先交换的元素交换后，影响了后交换的元素的交换，则需要修正后交换的元素下标

void SelectSort(int* arr, int sz)
{
	//闭区间: [begin, end]
	int begin = 0;
	int end = sz - 1;
	while (begin < end)//begin == end 最后一个数，天然有序
	{
		int mini = begin, maxi = begin;
		int i = 0;
		for (i = begin + 1; i <= end; i++)//俩下标初始化的就是begin，不用选第一个
		{
			if (arr[i] > arr[maxi])
				maxi = i;
			if (arr[i] < arr[mini])
				mini = i;
		}

		Swap(&arr[mini], &arr[begin]);

		//修正（预防）：如果maxi == begin，mini的数据到begin，真正的maxi的数据其实到mini的位置上
		if (maxi == begin)
			maxi = mini;
		Swap(&arr[maxi], &arr[end]);

		begin++;
		end--;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

稳定性

选择排序，选到最值后交换，会破坏相同元素的相对顺序，所以

选择排序是不稳定的

复杂度

时间复杂度

最好：

比较次数：O(n^2)，只选最小的比较次数为 (n-1) + (n-2) + … + 2 + 1，每次选最大和最小则快一倍，但数量级还是n^2

交换次数：O(1)，有序不用交换

O(n^2)

最坏：

比较次数：O(n^2)

交换次数：O(n)

O(n^2)

空间复杂度

O(1)

堆排序

思想

利用堆的性质，每次交换堆顶和最后一个元素，则排好最后一个元素，再把其视作堆外元素，最后对前面的元素重新建堆

操作

• 建大堆
• 单趟排序：
  • 选堆顶和堆尾的元素交换，则堆尾的元素排好
  • 每次把排好的“堆尾”元素视作堆外元素，并对堆顶重新向下调整建大堆
• 整体趟数：
  • 若元素个数为n，则排n趟

void Swap(int* e1, int* e2)
{
	assert(e1 && e2);

	int tmp = *e1;
	*e1 = *e2;
	*e2 = tmp;
}

void AdjustDown(int* arr, int sz, int parent)
{
	//建大堆，排升序
	assert(arr);
	
    //默认大孩子是左孩子
	int theChild = parent * 2 + 1;
	while (theChild < sz)
	{
        //如果大孩子是右孩子则修正
		if (theChild + 1 < sz && arr[theChild + 1] > arr[theChild])//注意右孩子下标合法性
		{
			theChild++;
		}
		if (arr[theChild] > arr[parent])
		{
			Swap(&arr[parent], &arr[theChild]);
            //迭代往下走
			parent = theChild;
			theChild = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void HeapSort(int* arr, int sz)
{
	//1.建大堆
	int i = 0;
	for (i = (sz - 2) / 2; i >= 0; i--)//从最后一个结点的父节点开始（最后一层不用调整，天然是堆）
	{
		AdjustDown(arr, sz, i);
	}

	//2. 选数
	i = 1;
	while (i < sz)
	{
		Swap(&arr[0], &arr[sz - i]);//交换堆顶和堆尾
		AdjustDown(arr, sz - i, 0);//堆尾视作堆外，对堆顶向下调整重新建堆
		i++;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

稳定性

建堆和向下调整都会打乱元素顺序，所以

堆排序是不稳定的

复杂度

时间复杂度

单趟排序，交换，并对堆顶向下调整重新建堆(O(logn))；趟数，n趟，所以堆排序的时间复杂度为

O(n*logn)

空间复杂度

原地建堆

O(1)

交换排序

冒泡排序

思想

冒泡排序，左右元素两两比较，左大于右就交换，一趟排好一个元素

操作

• 单趟排序：
  • 每趟排序从左到右两两比较并交换，直到走到已排序的元素就停
  • 每趟排好一个元素，所以需要排序的元素每次减少一个
• 整体趟数
  • 若元素个数为n，总共需要排n-1趟，最后一个元素天然有序

void BubbleSort(int* arr, int sz)
{
	int i = 0;
	int j = 0;
	for (j = 0; j < sz - 1; j++)
	{
		for (i = 0; i < sz - j - 1; i++)
		{
			if (arr[i] > arr[i + 1])
			{
				Swap(&arr[i], &arr[i + 1]);
				flag = 0;
			}
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

优化

当遍历一遍发现序列有序，直接跳出

void BubbleSort(int* arr, int sz)
{
	int i = 0;
	int j = 0;
	for (j = 0; j < sz - 1; j++)
	{
		int flag = 1;
		for (i = 0; i < sz - j - 1; i++)
		{
			if (arr[i] > arr[i + 1])
			{
				Swap(&arr[i], &arr[i + 1]);
				flag = 0;//不是有序就置0
			}
		}
		if (flag)//如果一趟下来还是1代表有序
			break;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

稳定性

相同的元素不交换，即使相同的元素不相邻，排好序后也是按照原来次序相邻起来，所以

冒泡排序是稳定的

复杂度

时间复杂度

最好： 当序列有序

未优化：

O(n^2)

优化：

O(n)

最坏：要进行 n-1 趟排序，每趟交换 n-i 次

O(n^2)

空间复杂度

O(1)

快速排序

思想

分治思想：单趟排序排好一个基准值(key)，key的左边都比key小，右边都比key大；再对左区间和右区间进行同样操作。

所以快速排序可以用递归来实现

操作

有三种单趟排序的方法：

Hoare法

• 设 begin 为当前区间的左闭区间，end 为当前区间的有闭区间

  左下标 L = begin，右下标 R = end

  设 L R 相遇位置为 meeti

  ​ 称 比 arr[keyi] 小的元素为 “小”比arr[keyi] 大的元素为“大”

  ​ 称 arr[keyi] 的左边都比key小，右边都比key大这种现象为 ”左小右大“

• 选 键值的下标 keyi

  • 左1位置作 keyi，则 R 先走
  • 右1位置作 keyi，则 L 先走

• R找小，

  • 找到则停
  • 遇到L，则交换 arr[keyi] 和 arr[meeti]

• L找大

  • 找到则交换 arr[L] 和 arr[R]
  • 遇到R，则交换 arr[keyi] 和 arr[meeti]

解惑：arr[meeti] 和 arr[keyi] 交换后一定符合”左小右大“吗？

答案是肯定的：

//[left, right]
int PartSort(int* arr, int left, int right)
{
	int keyi = left;
	//相遇则排好一趟
	while (left < right)
	{
		//R找小
        //left < right: 1. 这里也有可能相遇 2. 以免left和right错开
        //arr[right] >= arr[keyi]:相等也要过滤掉,1.相等的在左边右边没区别 2.不过滤会死循环——(88888888)怎么排?
		while (left < right && arr[right] >= arr[keyi])
		{
			right--;
		}

		//L找大
		while (left < right && arr[left] <= arr[keyi])
		{
			left++;
		}
		
        //相遇就不交换了
		if (left < right)
			Swap(&arr[left], &arr[right]);
	}

	int meeti = left;

	Swap(&arr[keyi], &arr[meeti]);

	return meeti;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

解惑：为什么key要选左1/右1，选中间不行吗？

可能有朋友已经想到了：（接近）有序情况，选左1/右1就出问题了，区间会分得很多，递归很深

非常容易栈溢出，怎么解决？针对有序情况，优化选key

优化选key

1. 随机选 key （是一种办法，但是不那么彻底）
2. 选中间位置作 key

解惑：那先前实现的单趟排序不就失效了吗！

：选到中间位置作key后，arr[begin] 和 arr[keyi]交换，逻辑还是能用原来的逻辑

解惑：如果中间位置选到很小/很大，换到左1后，还是会导致”区间分得多，递归深“的情况嘞？

前辈给出三数取中的方法

3. 三数取中
   1. 在 arr[begin] 、arr[mid]、 arr[end] 中选出中间值
   2. 这样一来，换到左1的最坏情况也只可能是次小/次大，缓解了“选中间作key””区间分得多，递归深”的痛点

优化选key后的Hoare单趟排序：

int GetMidIndex(int* arr, int left, int right)
{
	int mid = left + (right - left) / 2;
//  int mid = rand()%(right - left) + left;//增加了一定随机性
	if (arr[left] < arr[mid])
	{
		if (arr[right] < arr[left])
			mid = left;
		else if (arr[right] > arr[mid])
			mid = mid;
		else
			mid = right;
	}
	else//arr[left] > arr[mid]
	{
		if (arr[right] > arr[left])
			mid = left;
		else if (arr[mid] > arr[right])
			mid = mid;
		else
			mid = right;
	}
	return mid;
}

int PartSort_Hoare(int* arr, int left, int right)
{
	//中间作key，优化排（接近）有序数组的递归深度：O(N) ==> O(logN)
	int mid = GetMidIndex(arr, left, right);

	//单趟排序走的还是左1作key的逻辑，才能保证单趟排成
	Swap(&arr[mid], &arr[left]);

	int keyi = left;
	while (left < right)
	{
		//R找小
		while (left < right && arr[right] >= arr[keyi])
			right--;

		//L找大
		while (left < right&& arr[left] <= arr[keyi])
			left++;
        
		if (left < right)
			Swap(&arr[left], &arr[right]);
	}

	int meeti = left;

	Swap(&arr[keyi], &arr[meeti]);

	return meeti;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

挖坑法

• 初始状态：L作坑，其下标存为key
• (1) R找小，扔进坑，R作坑
• (2) L找大，扔进坑，L作坑
• 重复 (1) (2)
• 最终，L R 相遇，交换 arr[keyi] 和 arr[meeti]

int PartSort_Hole(int* arr, int left, int right)
{
	int mid = GetMidIndex(arr, left, right);
	Swap(&arr[mid], &arr[left]);

	int key = arr[left];
	//L作坑
	int hole = left;
	while (left < right)
	{
		//R找小，扔进坑，R作坑
		while (left < right && arr[right] >= key)
			right--;
		arr[hole] = arr[right];
		hole = right;

		//L找大，扔进坑，L作坑
		while (left < right && arr[left] <= key)
			left++;
		arr[hole] = arr[left];
		hole = left;
	}
	//meet
	int meeti = hole;
	arr[meeti] = key;

	return meeti;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

前后指针法

此方法理解起来较为抽象，但写起来十分简洁方便，不像前两种方法易错的地方较多

• cur找小，找到则停
• ++prev
  • 如果 prev != cur，交换 arr[prev] 和 arr[cur]
  • 如果 prev == cur，不交换
• 当cur越界，代表找完，排好序了

prev == cur 为什么就不交换呢，跟自己交换没必要——比较一下和交换一下的性能损耗相比，肯定是比较来得低

int PartSort3(int* arr, int left, int right)
{
	int mid = GetMidIndex(arr, left, right);
	Swap(&arr[mid], &arr[left]);
	
  //int key = arr[left];
	int keyi = left;

	int prev = left;
	int cur = prev + 1;
	
    //cur越界：找完小的，prev的左边全小，prev右边全大
	while (cur <= right) 
	{
        //++prev == cur 没必要交换
		if (arr[cur] < arr[keyi] && ++prev != cur)		
			Swap(&arr[prev], &arr[cur]);

		cur++;
	}

	//键值存是的值：
	//Swap(&arr[prev], &key);错！key在这里是单趟排序的局部变量，我们要和arr[left]换
	//Swap(&arr[prev], &arr[left]);//这才对
    //键值存的是下标：
	Swap(&arr[prev], &arr[keyi]);

	return prev;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

整体排序

递归——每次排好 arr[meeti]，分出左区间[beign, meeti-1] 和 右区间 [meeti+1, end]，再对左右区间快排

//[begin, end]
void QuickSort(int* arr, int begin, int end)
{
	//meeti位置符合有序 + 左区间有序 + 有区间有序 = 整体有序
	// [begin, meeti-1] - meeti - [meeti+1, end]
		//1.begin > end:超出范围
		//2.begin == end:一个数天然有序
    if(begin >= end)
        return;
    
		//排好meeti
		int meeti = PartSort3(arr, begin, end);

		//排好左右子区间
		QuickSort(arr, begin, meeti - 1);
		QuickSort(arr, meeti + 1, end);
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

…

没想到吧，还还还还有可以优化的地方！

优化小区间

如图所说，小区间内数很少，却消耗巨大，不如粗暴便捷地直接调用插入排序

那什么算是小区间？

其实小区间没有确切标准，8-15左右都可以的

这里就把小区间定义为 含有 8个数或以内 的区间

//[begin, end]
void QuickSort(int* arr, int begin, int end)
{
	if (begin >= end)
		return;

	if (end - begin + 1 <= 8)//小区间优化：后三层直接排
	{
		InsertSort(arr + begin,//可能是上一层的左子区间/右子区间
			end - begin + 1);//左闭右闭，如 [0,9] 有 9 - 0 + 1 = 10个数据
	}
	else
	{
		int meeti = PartSort3(arr, begin, end);

		QuickSort(arr, begin, meeti - 1);
		QuickSort(arr, meeti + 1, end);
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

稳定性

快速排序是不稳定的

复杂度

时间复杂度

O(n * logn)

空间复杂度

O(1)

快速排序非递归

为了解决彻底递归深度深的痛点，我们来试着把它改成非递归

思路：

递归深度深，栈的空间又小，会栈溢出…

那不如把函数递归“载体”换一个，在堆上手动开辟一个栈（数据结构的栈），栈帧里存什么，我们堆上的栈里就存什么！

核心思路：在堆上创建“栈帧”

快排的递归，栈帧内存储的最关键的数据是什么？区间。有了区间就能不断排序、分区间，排序、分区间…keyi都是可以算的

操作

在用数据结构栈存区间的时候要牢记 后进先出 原则，贴近递归的写法：

• 先递归左区间：就得先入右区间，后入左区间，这样才能先取左区间来递归
• 先取end：先入begin

void QuickSortNonR(int* arr, int begin, int end)
{
	ST st;
	StackInit(&st);
	
    //先入begin
	StackPush(&st, begin);
    //后入end
	StackPush(&st, end);

	while (!StackEmpty(&st))
	{
		//先取end
		int right = StackTop(&st);
		StackPop(&st);
		//后取begin
		int left = StackTop(&st);
		StackPop(&st);

		if (left >= right)//1.只有一个值  2.区间非法
			continue;  
				
		int keyi = PartSort_Pointer(arr, left, right);

		//先入右区间
		StackPush(&st, keyi + 1);
		StackPush(&st, right);
		//后入左区间
		StackPush(&st, left);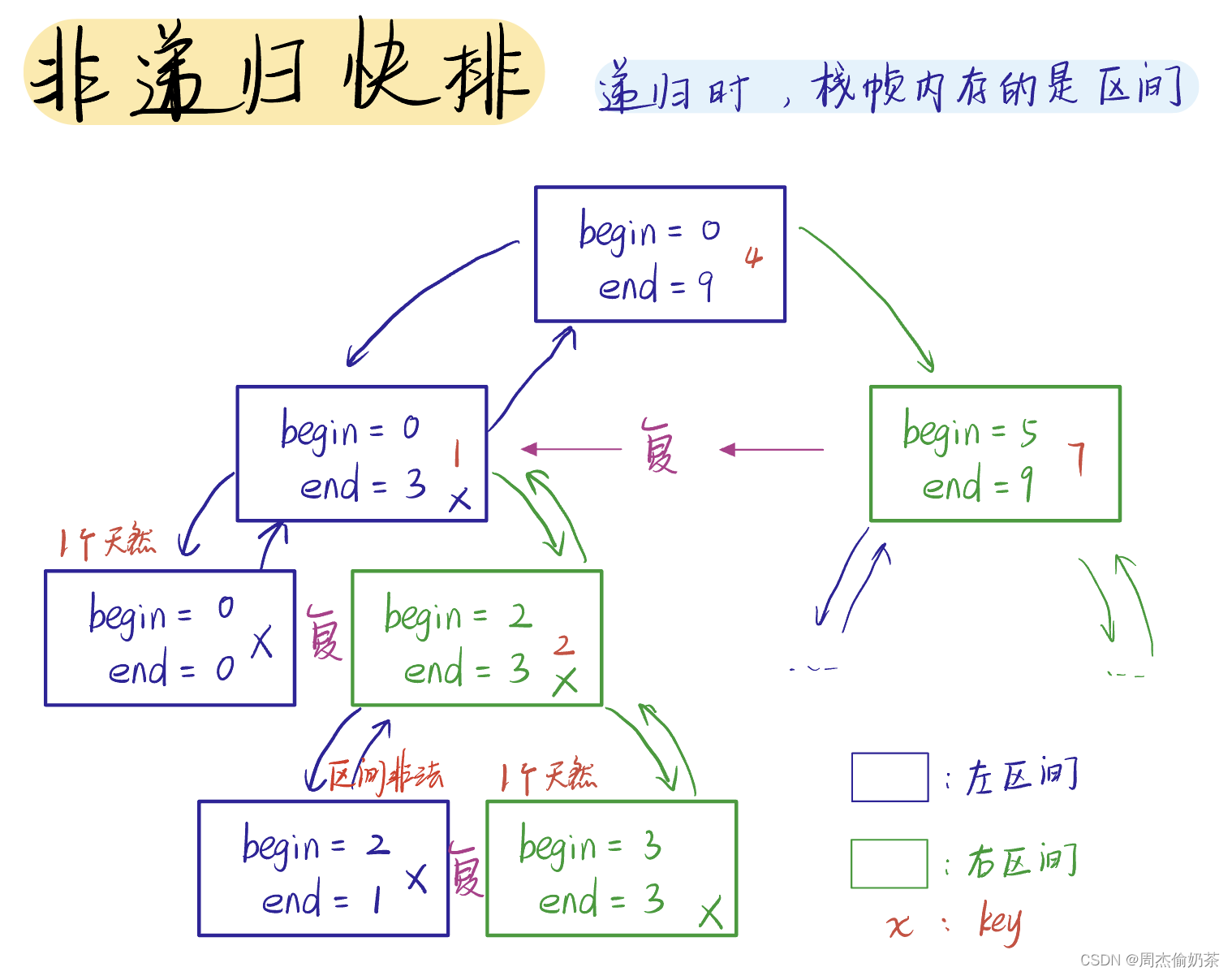![请添加图片描述](https://img-blog.csdnimg.cn/8d4a4b5184f44fd88e3e84bcda002f61.png)

		StackPush(&st, keyi - 1);
	} 

	StackDestroy(&st);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

数据结构栈的实现可以看博主之前发的博客

归并排序

思想

分治思想，将两个已有序区间合并，并使之合并后仍然有序

• 左有序右有序：分解区间至一个数，往回归并

• 归并：对于两个有序区间，取小的尾插到tmp，再拷贝回原数组

  *开辟额外数组来归并（可以在原数组进行尾插操作吗？不行，会把有效数据覆盖）

注：归并操作其实是往回返的，为了方便看就往下画了

操作

• 单趟排序：归并两个有序区间，使之合并后依然有序
• 整体趟数：递归到区间内只有一个数（最小规模），而后往回归并到最开始的左区间和右区间有序为止

void Merge(int* arr, int* tmp, int begin, int mid, int end)
{
	//[beign, mid]  [mid+1, end]
	int i = begin, j = mid + 1, k = begin;
	while (i <= mid && j <= end)
	{
		if (arr[i] <= arr[j])
			tmp[k++] = arr[i++];
		else
			tmp[k++] = arr[j++];
	}

	while (i <= mid)
		tmp[k++] = arr[i++];
	while (j <= end)
		tmp[k++] = arr[j++];
	for (i = begin; i <= end; i++)
		arr[i] = tmp[i];
}

void MergeSort(int* arr, int* tmp, int begin, int end)
{
	if (begin >= end)
		return;
    
	//[beign, mid]  [mid+1, end]
	int mid = begin + (end - begin) / 2;
    //左有序
	MergeSort(arr, tmp, begin, mid);
    //右有序
	MergeSort(arr, tmp, mid + 1, end);
    //归并
	Merge(arr, tmp, begin, mid, end);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

稳定性

归并取小的尾插，相等的时候左边的先插，就可以不变相对顺序，所有

稳定

复杂度

时间复杂度

每次接近二分，整体结构类似二叉树：高度h ~= log2n，每层尾插n次，所以归并排序的时间复杂度是

O(N*logN)

空间复杂度

待排序的元素有n个，就需要开辟n个空间，所以归并排序的空间复杂度是

O(n)

这也是归并排序的缺陷

归并非递归

思想

想改归并非递归，得先吃透递归的本质

归并的递归，就是 一一归，二二归，四四归…—— 先分解到最小规模，再往回归并

类似斐波那契数列的递归呢！要求第n个斐波那契数：第一个+第二个 ==> 第三个， 第二个+第三个 ==> 第四个，直接从最小规模起算

我们对归并非递归也试试

操作

• 给一个增量gap，代表每次要归并的规模
• 每趟排序按照gap，归整个数组
• 当gap >= sz，也就归并完成了

如何控制gap（规模）呢？

• right= left + (gap - 1) ：元素个数是 右闭 - 左闭 + 1，而gap代表归并的元素个数

  right - left + 1 = gap ==> right = left + (gap-1)

• j += 2*gap ：每次是两组归并，+=2*gap 就是跳到单趟归并的下一组

严谨地看，此处计算的下标明显存在越界风险

遇到了非法区间

• 第一组部分越界（end1越界）：没必要归并，[8]在原地等着最后的归并就行
• 第二组全部越界（begin2 end2越界）：不存在的区间，不理会
• 第二组部分越界（end2越界）：第二组区间内仍有有效数据，要往下归

void MergeSortNonR(int* arr, int left, int right, int* tmp)
{
    //元素个数：右闭 - 左闭 + 1
	int sz = right - left + 1;
	int gap = 1;
	while (gap < sz)
	{
		int j = 0;
		for (j = 0; j < sz; j += 2 * gap)
		{
			int left1 = j;
			int right1 = j + (gap - 1);
			int mid1 = left1 + (right1 - left1) / 2;

			int left2 = j + gap;
			int right2 = j + gap + (gap - 1);
			int mid2 = left2 + (right2 - left2) / 2;

			if (right1 >= sz)
			{
				break;
			}

			if (left2 >= sz)
			{
				break;
			}

			if (right2 >= sz)
			{
				right2 = sz - 1;
			}


			Merge(arr, left1, mid1, right1, tmp);
			Merge(arr, left2, mid2, right2, tmp);
		}

		gap *= 2;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

• while(gap < sz)
• gap *= 2 ：每次归并两组，所以规模翻倍

非比较排序

计数排序

思想

计数排序，是对哈希直接定址法的变形应用，开辟一块空间，将元素的值映射成空间的下标并计数

而映射也分直接映射和相对映射：

• 直接映射，待排序元素有N个，就开辟N个元素的空间
• 相对映射，根据待排序元素的最值，确定范围，根据范围开辟空间

操作

• 找最值 max min ，确定范围 range
• 开辟range个元素的空间 countArr
• 将待排序元素的值，相对映射成 countArr 的下标
• 将 countArr 中记录的次数，映射成值拷贝回数组

void CountSort(int* arr, int sz)
{
	//遍历找出最大最小
	//int max = INT_MIN;
	int max = arr[0];

	//int min = INT_MAX;
	int min = arr[0];

	int i = 0;
	for (i = 1; i < sz; i++)
	{
		if (arr[i] > max)
			max = arr[i];
		if (arr[i] < min)
			min = arr[i];
	}

	//确定范围range
	int range = max - min + 1;
    //开辟range个空间
	int* countArr = (int*)calloc(range, sizeof(int));
	assert(countArr);

	//相对映射：将值相对映射成下标
	for (i = 0; i < sz; i++)
	{
		int index = arr[i] - min;
		countArr[index]++;
	}

	int j = 0;
	//将下标映射成值，拷贝
	for (i = 0; i < range; i++)
	{
		while (countArr[i]--)
			arr[j++] = i + min;
	}

	free(countArr);
	countArr = NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

稳定性

稳定

复杂度

时间复杂度

求最值 O(N) + 相对映射 O(N) + 排序 O(rang)

O(N + range)

空间复杂度

O(range)

综上，数据范围集中时用计数排序十分合适

性能测试

void TestOp()
{
	const int N = 100000 ;
	int* a1 = (int*)malloc(sizeof(int) * N);
	assert(a1);
	int* a2 = (int*)malloc(sizeof(int) * N);
	assert(a2);
	int* a3 = (int*)malloc(sizeof(int) * N);
	assert(a3);
	int* a4 = (int*)malloc(sizeof(int) * N);
	assert(a4);
	int* a5 = (int*)malloc(sizeof(int) * N);
	assert(a5);
	int* a6 = (int*)malloc(sizeof(int) * N);
	assert(a6);
	int* a7 = (int*)malloc(sizeof(int) * N);
	assert(a7);

	for (int i = 0; i < N; ++i)
	{
		a1[i] = rand() + i;
		a2[i] = a1[i];
		a3[i] = a1[i];
		a4[i] = a1[i];
		a5[i] = a1[i];
		a6[i] = a1[i];
		a7[i] = a1[i];
	}

	int begin1 = clock();
	InsertSort(a1, N);
	int end1 = clock();

	int begin2 = clock();
	ShellSort(a2, N);
	int end2 = clock();

	int begin3 = clock();
	SelectSort(a3, N);
	int end3 = clock();

	int begin4 = clock();
	HeapSort(a4, N);
	int end4 = clock();

	int begin5 = clock();
	QuickSort(a5, 0, N - 1);
		//1.快排排有序数组，递归太深
		//QuickSort(a4, 0, N - 1);
		//2.用三数取中优化
		//QuickSort(a4, 0, N - 1);
		//3.小区间优化
		//QuickSort(a4, 0, N - 1);
	int end5 = clock();

	int begin6 = clock();
	MergeSort(a6, N);
	int end6 = clock();

	int begin7 = clock();
	CountSort(a7, N);
	int end7 = clock();

	printf("InsertSort:%d\n", end1 - begin1);
	printf("ShellSort:%d\n", end2 - begin2);
	printf("SelectSort:%d\n", end3 - begin3);
	printf("HeapSort:%d\n", end4 - begin4);
	printf("QuickSort:%d\n", end5 - begin5);
	printf("MergeSort:%d\n", end6 - begin6);
	printf("CountSort:%d\n", end7 - begin7);


	free(a1);
	free(a2);
	free(a3);
	free(a4);
	free(a5);
	free(a6);
	free(a7);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80

使用场景

遇事不决就快排，谁更优势就用谁

• 直接插入排序：较有序
• 希尔排序：较有序
• 选择排序：这家伙还是算了
• 堆排序：TopK（建堆已经O(N)，消耗大）
• 冒泡排序：效率也太低
• 快速排序：综合起来非常好，能适应大多场景，效率也挺好
• 归并排序：主要是外排序（对内存外，如磁盘中的数据排序）
• 计数排序：数据的值跨度不大时极好

---

不知不觉数据结构初阶就学完了，不得不说这东西蛮有魅力的，继续前进吧

…

这里是培根的blog，期待与你共同进步！

下期见！