深度学习笔记(三):神经网络之九种激活函数Sigmoid、tanh、ReLU、ReLU6、Leaky Relu、ELU、Swish、Mish、Softmax详解_leakyrelu函数和mish

1.什么叫激活函数

激活函数可作用于感知机(wx+b)累加的总和 ,所谓的激活就是把输出值必须要大于，节点才可以被激活，不然就处于睡眠状态。

2.激活函数的作用

提供网络的非线性建模能力。如果没有激活函数，那么该网络仅能够表达线性映射，此时即便有再多的隐藏层，其整个网络跟单层神经网络也是等价的。因此也可以认为，只有加入了激活函数之后，深度神经网络才具备了分层的非线性映射学习能力。由于输出值是有限的，基于梯度的优化方法会更加稳定。输出值是无限的时候，模型的训练会更加高效，但往往这个时候学习率需要更小。

3.激活函数的类型

Sigmoid、tanh、ReLU、ReLU6、Leaky Relu、ELU、Softmax

4.Sigmoid/Logistic

函数定义:

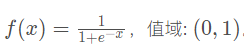
函数图像：

Sigmoid函数的导数是其本身的函数，即f′(x)=f(x)(1−f(x))，计算非常方便。

这可用做神经网络的阈值数，将变量映射到0，1之间。由于在图像两端，该函数导数趋近于0，也就是说sigmoid的导数只有在0附近的时候有比较好的激活性，在正负饱和区的梯度都接近于0，所以这会造成梯度弥散(也就是说长时间权值得不到更新，loss一直保持不变)，从而网络参数很难得到有效训练。一般来说， sigmoid 网络在 5 层之内就会产生梯度消失现象。

代码实现：

"""pytorch 神经网络"""
import torch.nn.functional as F
F.sigmoid(x)
1
2
3

# sigmoid函数在torch中如何实现

import torch
# a从-100到100中任取10个数
a = torch.linspace(-100,100,10)
print(a)
# 或者F.sigmoid也可以 F是从from torch.nn import functional as F
b = torch.sigmoid(a)
print(b)
1
2
3
4
5
6
7
8
9

运行结果：

从图中可知道通过sigmoid函数把全部的值映射到0，1之间，且不均与变化。

5.tanh

函数定义:

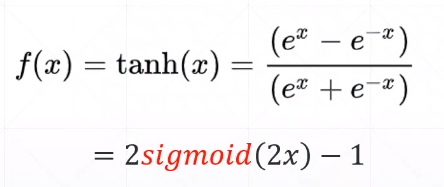值域为(-1,1)

tanh()为双曲正切。在数学中，双曲正切tanh是由基本双曲函数双曲正弦和双曲余弦推导而来。

函数图像

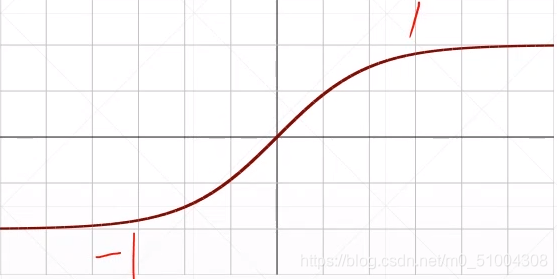
tanh和sigmoid的关系:sigmoid的X轴平面压缩1/2，Y轴放大两倍，再向下平移一个单位得到tanh。
tanh函数的导数：f’(x)=1-[f(x)]^2.

优点：

• 它解决了Sigmoid函数的不是zero-centered输出问题。

缺点：

• 梯度消失（gradient vanishing）的问题和幂运算的问题仍然存在。
  为了解决梯度消失问题，我们来讨论另一个非线性激活函数——修正线性单元（rectified linear
  unit，ReLU），该函数明显优于前面两个函数，是现在使用最广泛的函数。

代码实现：

# tanh函数在torch中如何实现
import torch
a = torch.linspace(-10,10,10)
b = torch.tanh(a)
print(a)
print(b)
1
2
3
4
5
6

运行结果：

6.ReLU

函数定义:

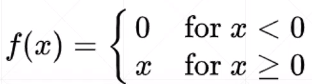
函数图像：

ReLU函数非常适合于做深度学习，因为当Z<0的时候梯度为0，Z>0的时候梯度为1，因此在做向后传播的时候，计算非常方便，不放大也不缩小，很大程度上不会出现梯度离散和梯度爆炸的情况。

代码实现:

"""pytorch 神经网络"""
import torch.nn as nn
Re=nn.ReLU(inplace=True)
1
2
3

# ReLU函数在torch中如何实现
import torch
a = torch.linspace(-1,1,10)
b = torch.relu(a)
print(a)
print(b)
1
2
3
4
5
6

运行结果：

7.ReLU6

函数定义:

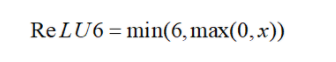
函数图像：

主要是为了在移动端float16的低精度的时候，也能有很好的数值分辨率，如果对ReLu的输出值不加限制，那么输出范围就是0到正无穷，而低精度的float16无法精确描述其数值，带来精度损失。

代码实现:

"""pytorch 神经网络"""
import torch.nn as nn
Re=nn.ReLU6(inplace=True)
1
2
3

# ReLU函数在torch中如何实现
import torch
import torch.nn as nn

x = torch.linspace(-5, 10, 20)
relu6 = nn.ReLU6()
y = relu6(x)
print(x)
print(y)
1
2
3
4
5
6
7
8
9

运行结果：

8.Leaky ReLU

函数定义:

在输入 x < 0 x < 0x<0 时， 保持一个很小的梯度 γ \gammaγ． 这样当神经元输出值为负数也能有一个非零的梯度可以更新参数， 避免永远不能被激活，其中 γ是一个很小的常数， 比如 0.01． 当 γ < 1 时， Leaky ReLU 也可以写为

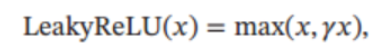
函数图像：

优点：

• 该函数一定程度上缓解了 dead ReLU 问题。

缺点：

• (1)使用该函数的结果并不连贯。尽管它具备 ReLU 激活函数的所有特征，如计算高效、快速收敛、在正区域内不会饱和。
• (2)Leaky ReLU 可以得到更多扩展。不让 x 乘常数项，而是让 x 乘超参数，这看起来比 Leaky ReLU
  效果要好。该扩展就是 Parametric ReLU。

代码实现:

"""pytorch 神经网络"""
import torch.nn as nn
LR=nn.LeakyReLU(inplace=True)
1
2
3

# tensorflow实现LeakyRelu函数
import tensorflow as tf
def LeakyRelu(x,leak = 2,name = 'LeakyRelu'):
    with tf.variable_scope(name):
        f1 = 0.5*(1+leak)
        f2 = 0.5*(1-leak)
        return f1*x+f2*tf.abs(x)

if __name__ == '__main__':
    a = LeakyRelu(4.0)
    print(a)
1
2
3
4
5
6
7
8
9
10
11

运行结果：

9.ELU

函数定义:

函数图像：

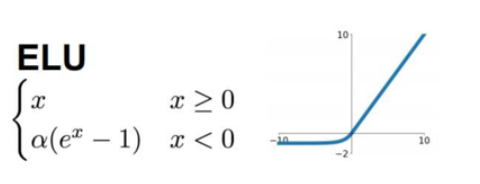
右侧的线性部分能够缓解梯度消失,左侧的软饱和能够对于输入变化鲁棒.而且收敛速度更快.

代码实现:

# ELU函数在numpy上的实现

import numpy as np
import matplotlib.pyplot as plt

def elu(x, a):
    y = x.copy()
    for i in range(y.shape[0]):
        if y[i] < 0:
            y[i] = a * (np.exp(y[i]) - 1)
    return y
if __name__ == '__main__':
    x = np.linspace(-50, 50)
    a = 0.5
    y = elu(x, a)
    print(y)
    plt.plot(x, y)
    plt.title('elu')
    plt.axhline(ls='--',color = 'r')
    plt.axvline(ls='--',color = 'r')
    # plt.xticks([-60,60]),plt.yticks([-10,50])
    plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

运行结果：

10.Swish

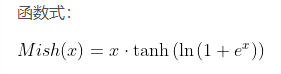
class Swish(nn.Module):
    def __init__(self):
        super(Swish, self).__init__()
 
    def forward(self, x):
        x = x * F.sigmoid(x)
        return x
1
2
3
4
5
6
7

11.Mish

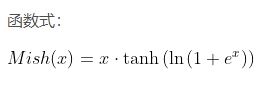
相比Swish有0.494%的提升，相比ReLU有1.671%的提升。
为什么Mish表现的更好：

• 以上无边界(即正值可以达到任何高度)避免了由于封顶而导致的饱和。理论上对负值的轻微允许允许更好的梯度流，而不是像ReLU中那样的硬零边界。最后，可能也是最重要的，目前的想法是，平滑的激活函数允许更好的信息深入神经网络，从而得到更好的准确性和泛化。要区别可能是Mish函数在曲线上几乎所有点上的平滑度

#-------------------------------------------------#
#   MISH激活函数
#-------------------------------------------------#
class Mish(nn.Module):
    def __init__(self):
        super(Mish, self).__init__()

    def forward(self, x):
        return x * torch.tanh(F.softplus(x))
1
2
3
4
5
6
7
8
9

12.Softmax

函数定义:

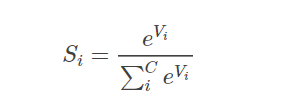
Vi表示第i个神经元的输出，其实就是在输出后面套一个这个函数

函数作用:用于处理多分类问题，将N个输出的数值全部转换为N个相对概率。比如说
这里有个特点，就是这里所有的概率值全部加起来等于1. S1 = 0.8390，对应的概率最大，概率越大预测为第1类的可能性更大。

代码简单实现:

# Softmax实现
import numpy as np
def Softmax(x):
    n = np.exp(x)/np.sum(np.exp(x))
    return n
if __name__ == '__main__':
    x = [3.0,1.0,2.0]

    a = Softmax(x)
    print(a)
1
2
3
4
5
6
7
8
9
10

运行结果：

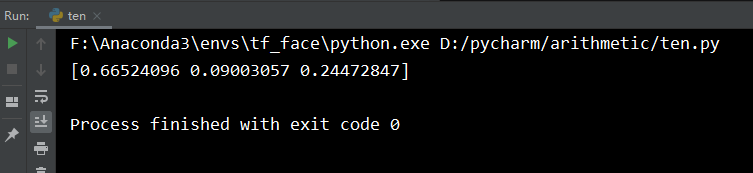
一维和二维矩阵的Softmax代码实现:

# Softmax二维和三维矩阵的实现
import numpy as np



def Softmax(x):
    print("orig_shape", x.shape)

    if len(x.shape) > 1:
        # 矩阵 轴用来为超过一维的数组定义的属性，二维数据拥有两个轴：第0轴沿着行的垂直往下，第1轴沿着列的方向水平延伸。
        # 关键词：轴具有方向，且axis=0，即0轴，从上到下；axis=1，即1轴，从左到右。axis=-1也就是代表倒数第一个，如果对于矩阵是一个shape=[3,4,5],axis=-1就等于axis=2，也就是得到一个[3,4]的矩阵，
        tmp = np.max(x, axis=1)
        x -= tmp.reshape((x.shape[0], 1)) # 变为两行一列
        x = np.exp(x)
        y = x / np.sum(x, axis=1).reshape((x.shape[0], 1))
        print("matrix")
        print(y)
        return y
    else:
        # 向量
        x -= np.max(x)  # scores becomes [-666, -333, 0]
        y = np.exp(x) / np.sum(np.exp(x))
        print("Vector quantity")
        print(y)
        return y


if __name__ == '__main__':
    x = np.array([1,2,3,4])
    x1 = np.array([[1,2,3,4],[1,2,3,4]])
    Softmax(x)
    Softmax(x1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

运行结果：

喜欢记得点赞收藏 3Q思密达~