热门标签
热门文章
- 1力扣热题Top100--每日两题_力扣top100
- 2pytorch利用梯度下降求方程的最小值_day2_pytorch 梯度下降法 最小化
- 3HTML 颜色_html颜色
- 4修改linux系统的root密码_linux修改root用户密码的几种方法
- 5一文快速带您了解 KMM、Compose 和 Flutter 的现状 | 开发者说·DTalk
- 6Vscode 浏览器纯 v8 环境联调 js_node 运行纯净v8
- 7【数据库】快速判断一对多,多对多关系,并建立数据库实体之间的映射_一对多关系1和n标注的位置要区分吗
- 8【Python机器学习】文本特征提取及文本向量化讲解和实战(图文解释 附源码)_文本向量化和特征提取的关系
- 9Stable-Diffusion-webui mac m1安装_installing requirements for codeformer
- 10PostgreSQL 优化器案例之 - order by limit 索引选择问题
当前位置: article > 正文
数值分析第六章知识点总结——插值与逼近_函数的插值与逼近知识点
作者:不正经 | 2024-03-05 19:23:32
赞
踩
函数的插值与逼近知识点
插值与逼近
--------本章节总体逻辑:
- 对于在实验中获得的数据来说,通常时候需要拟合成函数的形式,这样方便计算、预测等。
- 对于两个点、三个点可以采用最简单的Lagrange插值多项式的方法进行拟合,分别为线性差值多项式和抛物线插值多项式。
- 当实验数据多的时候,也就意味着需要进行插值的被插值函数的自变量很多,即n+1个不共线的点,可以通过通过插值生成n次Lagrange插值多项式。
- 但这种情况下,每增加一个点,都需要重新计算一下这n+1次的插值多项式,很不方便,基于这个,提出了通过差商表示的Newton插值多项式,这种插值多项式的形式,可以很好的实现增加一个点之后生成新的插值多项式。
- 但是无论是Lagrange插值多项式,还是Newton插值多项式的条件都是连接点处函数值相等,因此插值后的多项式很可能会出现多个不可导点,基于这种原因,提出了Hermite插值多项式。
- 但随着n的增大,多项式的次数过高,在远离插值节点的地方波动、偏差会特别大,即会出现龙格(Runge)现象。这时,我们就可以讨论分段插值的方法。
- 分段插值即是按照原n个插值节点分割成n-1个区间,对每个区间分别采用Lagrange插值多项式,Hermite插值多项式的方法。
- 分段插值虽然在计算层面有很好的提高,同时避免了Runge现象的发生,但是它很难解决插值函数不光滑的问题,这时,提出了三次样条插值多项式。
- 三次样条插值方法根据,已知条件是一阶导数、二阶导数分为了三转角方法、三弯矩方法。每种方法分别对三种补充条件(已知端点处的一阶导数、已知端点处的二阶导数、端点处的一阶导二阶导相等)分别讨论。
- 上述多种插值方法都属于对目标函数的逼近,插值方法也是要求严格的经过被插值函数的每一个节点。除了这种逼近函数的方法,还有一种逼近函数的方法——拟合。
- 最小二乘法,即是通过平方范数对函数的一种逼近,这种拟合的方法不要求严格经过被插值函数的每一个节点,只要求函数与拟合结果的函数的差值向量的平方范数达到最小值。
--------以下为各部分具体知识点:
一、多项式插值问题
- 定义:通过已知数据得到函数的近似解析表达式。
- 相关概念:被插值函数、插值函数、插值节点、插值条件、插值方法
- 性质:给定n+1个互异节点的函数值,则满足函数值相等的插值条件的n次插值多项式是唯一存在的。
二、Lagrange插值多项式
- 线性插值多项式
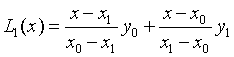
- 抛物线插值多项式
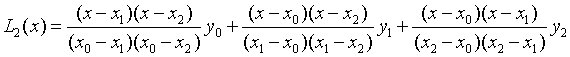
- n次Lagrange插值多项式
(1)为了方便多项式形式的统一表达,引入如下定义:

(2)节点基函数

- Lagrange插值余项
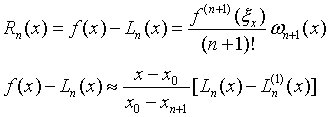
三、Newton插值多项式
- 差商
(1)定义(一阶差商,二阶差商,k阶差商)
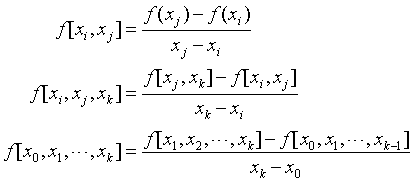
(2)性质
- k阶差商可以表示成函数值的线性组合
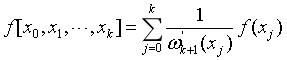
- 差商对节点具有对称性
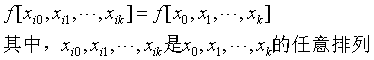
- n次多项式f(x)的k阶差商,当k≤n时,是一个关于x的n-k次多项式;当k>n时,恒等于0。
- 若f(x)具有k阶连续导数,则:

- Newton插值多项式

- Newton插值余项与Lagrange插值余项
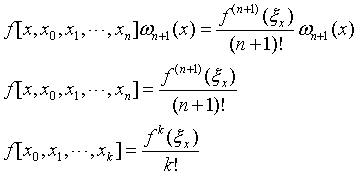
四、Hermite插值多项式
- 定义:不仅要求在节点处函数值相同,还要求在部分或全部节点处具有相同的导数值。
- 方法:承袭法,基函数法
例:

(1)承袭法
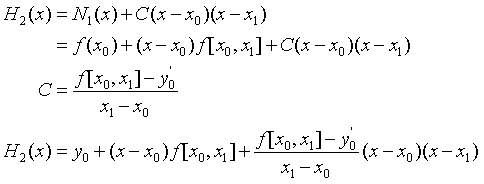
(2)基函数法
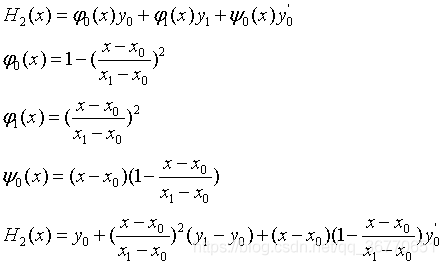
- Hermite插值多项式
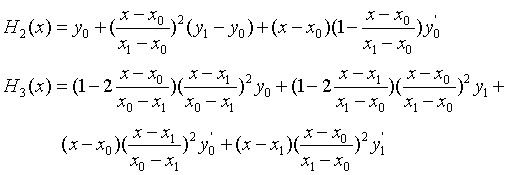
- Hermite插值余项
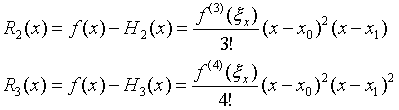
五、分段插值多项式
根据插值条件构建插值多项式时,插值多项式的次数随着节点个数的增加而升高,而实际应用上,很少采用高于七次的插值多项式。因此,为了提高多项式的逼近精度,就需要引进分段插值方法。
- 分段线性插值
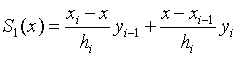
- 分段二次插值
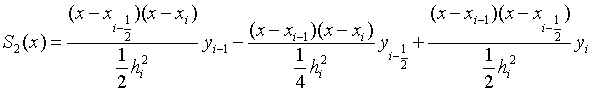
- 分段三次Hermite插值

- 误差分析:
(1)分段线性插值
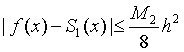
(2)分段二次插值
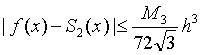
(3)分段三次Hermite插值

六、三次样条插值多项式
- 定义:每个小区间上S(x)为三次多项式,且二阶连续可微。在两端点各加一个条件称为边界条件。具体包括以下三种。根据初始方程的未知数不同,可分为三转角方法和三弯矩方法。
(1)两端点的一阶导数值已知。
(2)两端点的二阶导数值已知。
(3)函数为周期函数,即两端点的一阶导数值、二阶导数值相等。 - 三转角方法:未知数为一阶导数
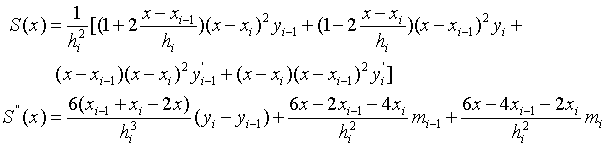
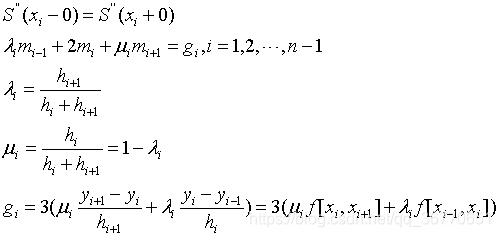
- 三弯矩方法:未知数为二阶导数

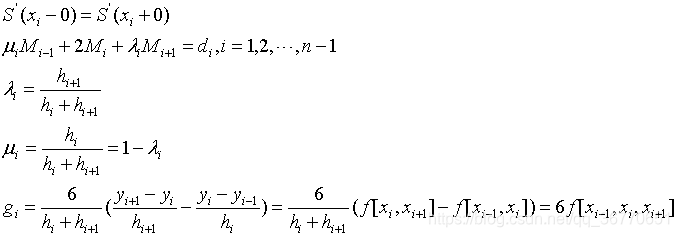
- 不同边界条件两种方法的未知数角标
| 三次样条插值函数方法 | 两端点一阶导已知 | 两端点二阶导已知 | 周期函数 |
|---|---|---|---|
| 三转角方法 | 1~n-1 | 0~n | 1~n |
| 三弯矩方法 | 0~n | 1~n-1 | 1~n |
七、正交多项式
- 定义:由线性无关函数组经过Schemite正交化过程得到的多项式称为[a,b]上的正交多项式。

- 重要概念:权函数(见“1”)
- 例题

八、数据拟合的最小二乘法
- 定义:采用函数系(多项式函数系,三角函数系,指数函数系,正交多项式等)求得的拟合曲线称为多项式拟合曲线。在计算误差向量的范数时,采用2-范数的方法即为最小二乘法。
- 计算方法:
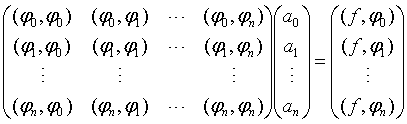
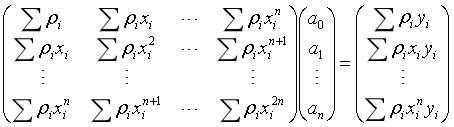
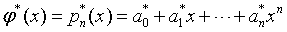
九、常考题型及解题思路
- 求插值多项式
- 套公式即可
- 或设相应的函数方程,之后代入已知点,求解系数
- 求近似函数值,并求相应误差界
- 求插值多项式(见题型1)
- 套公式求误差界
- Lagrange相关证明
- 想定义
- 构造函数
- 差商相关证明
- 想数学归纳法
- 想高阶差商与拉格朗日插值余项的关系
- 求差商表、Newton插值多项式
- 一步步求就好了
- 求三次Hermite插值多项式
- 构造基函数
- 求相应的函数表达式
- 最小二乘法求方程组近似解
- 构造平方和形式(向量二范数)
- 偏导等于0,求极值点及相应极值
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/不正经/article/detail/193301
推荐阅读
相关标签


