代码随想录Day50|123.买卖股票的最佳时机III、188.买卖股票的最佳时机IV

123.买卖股票的最佳时机III

文章讲解：代码随想录 (programmercarl.com)

题目链接：123. 买卖股票的最佳时机 III - 力扣（LeetCode）

题目：

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

分析：

1. 确定dp数组以及下标的含义

   一天一共就有五个状态，

   1. 没有操作
   2. 第一次买入
   3. 第一次卖出
   4. 第二次买入
   5. 第二次卖出

   dp[i] [j]中 i表示第i天，j为 [0 - 4] 五个状态，dp[i] [j]表示第i天状态j所剩最大现金。

2. 确定递推公式

   需要注意：dp[i] [1]，表示的是第i天，买入股票的状态，并不是说一定要第i天买入股票

   达到dp[i] [ 1]状态，有两个具体操作：

   • 操作一：第i天买入股票了，那么dp[i] [1] = dp[i-1] [0] - prices[i]
   • 操作二：第i天没有操作，而是沿用前一天买入的状态，即：dp[i] [1] = dp[i - 1] [1]

   dp[i] [1] = max(dp[i-1] [0] - prices[i], dp[i - 1] [1]);

   同理dp[i] [2]也有两个操作：

   • 操作一：第i天卖出股票了，那么dp[i] [2] = dp[i - 1] [1] + prices[i]
   • 操作二：第i天没有操作，沿用前一天卖出股票的状态，即：dp[i] [2] = dp[i - 1] [2]

   所以dp[i] [2] = max(dp[i - 1] [1] + prices[i], dp[i - 1] [2])

   同理可推出剩下状态部分：

   dp[i] [3] = max(dp[i - 1] [3], dp[i - 1] [2] - prices[i]);

   dp[i] [4] = max(dp[i - 1] [4], dp[i - 1] [3] + prices[i]);

3. dp数组如何初始化

4. 确定遍历顺序

   一定是从前向后遍历

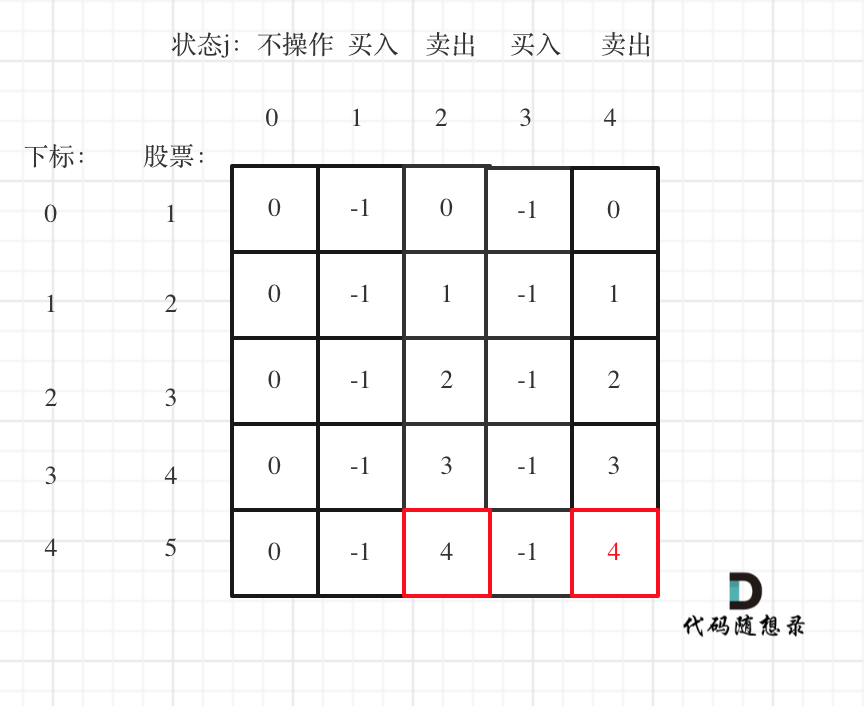
5. 举例推导dp数组

   以输入[1,2,3,4,5]为例

   

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if (prices.size() == 0) return 0;
        vector<vector<int>> dp(prices.size(), vector<int>(5,0));
        dp[0][1] = -prices[0];
        dp[0][3] = -prices[0];
        for (int i = 1; i < prices.size(); i++) {
            dp[i][0] = dp[i - 1][0];
            dp[i][1] = max(dp[i - 1][0] - prices[i], dp[i - 1][1]);
            dp[i][2] = max(dp[i - 1][1] + prices[i], dp[i - 1][2]);
            dp[i][3] = max(dp[i - 1][2] - prices[i], dp[i - 1][3]);
            dp[i][4] = max(dp[i - 1][3] + prices[i], dp[i - 1][4]);
        }
        return dp[prices.size() - 1][4];
    }
}; 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

188.买卖股票的最佳时机IV

文章讲解：代码随想录 (programmercarl.com)

题目链接：188. 买卖股票的最佳时机 IV - 力扣（LeetCode）

题目：

给定一个整数数组 prices ，它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

分析：

1. 确定dp数组以及下标的含义

在动态规划：123.买卖股票的最佳时机III (opens new window)中，我是定义了一个二维dp数组，本题其实依然可以用一个二维dp数组。

使用二维数组 dp[i] [j] ：第i天的状态为j，所剩下的最大现金是dp[i] [j]

j的状态表示为：

• 0 表示不操作
• 1 第一次买入
• 2 第一次卖出
• 3 第二次买入
• 4 第二次卖出
• …

大家应该发现规律了吧 ，除了0以外，偶数就是卖出，奇数就是买入。

题目要求是至多有K笔交易，那么j的范围就定义为 2 * k + 1 就可以了。

2. 确定递推公式

还要强调一下：dp[i] [1]，表示的是第i天，买入股票的状态，并不是说一定要第i天买入股票，这是很多同学容易陷入的误区。

达到dp[i] [1]状态，有两个具体操作：

• 操作一：第i天买入股票了，那么dp[i] [1] = dp[i - 1] [0] - prices[i]
• 操作二：第i天没有操作，而是沿用前一天买入的状态，即：dp[i] [1] = dp[i - 1] [1]

选最大的，所以 dp[i] [1] = max(dp[i - 1] [0] - prices[i], dp[i - 1] [1]);

同理dp[i] [2]也有两个操作：

• 操作一：第i天卖出股票了，那么dp[i] [2] = dp[i - 1] [1] + prices[i]
• 操作二：第i天没有操作，沿用前一天卖出股票的状态，即：dp[i] [2] = dp[i - 1] [2]

所以dp[i] [2] = max(dp[i - 1] [1] + prices[i], dp[i - 1] [2])

3. dp数组如何初始化

第0天没有操作，这个最容易想到，就是0，即：dp[0] [0] = 0;

第0天做第一次买入的操作，dp[0] [1] = -prices[0];

第0天做第一次卖出的操作，这个初始值应该是多少呢？

首先卖出的操作一定是收获利润，整个股票买卖最差情况也就是没有盈利即全程无操作现金为0，

从递推公式中可以看出每次是取最大值，那么既然是收获利润如果比0还小了就没有必要收获这个利润了。

所以dp[0] [2] = 0;

第0天第二次买入操作，初始值应该是多少呢？

不用管第几次，现在手头上没有现金，只要买入，现金就做相应的减少。

第二次买入操作，初始化为：dp[0] [3] = -prices[0];

所以同理可以推出dp[0] [j]当j为奇数的时候都初始化为 -prices[0]

4. 确定遍历顺序

从递归公式其实已经可以看出，一定是从前向后遍历，因为dp[i]，依靠dp[i - 1]的数值。

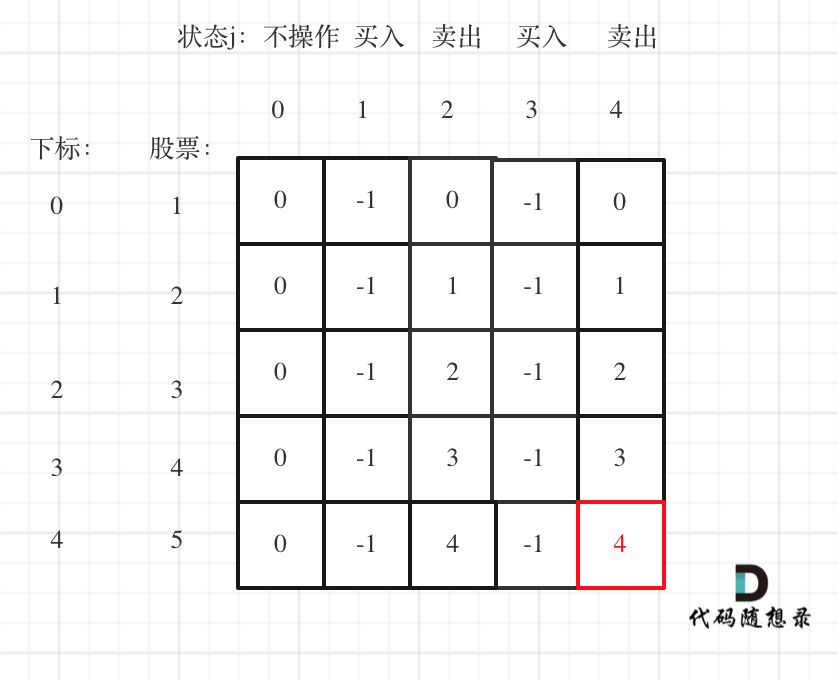
5. 举例推导dp数组

以输入[1,2,3,4,5]，k=2为例。

class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        if (prices.size() == 0) return 0;
        vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0));
        for (int j = 1; j < 2 * k; j += 2) {
            dp[0][j] = -prices[0];
        }
        for (int i = 1; i < prices.size(); i++) {
            for (int j = 0; j < 2 * k - 1; j += 2) {
                dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
                dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
            }
        }
        return dp[prices.size() - 1][2 * k];
    }
}; 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17