- 1智慧政务 大数据平台项目建设方案_智慧政务大数据云平台建设方案
- 2RK3588 USB蓝牙调试_awnb108_rk3588 android12调试蓝牙
- 3怎样在mysql里复制一张表_如何用sql语句复制一张表
- 4错误:[IM002] [Microsoft][ODBC驱动程序管理器]未发现数据源名称并且未指定默认驱动程序(0)_im002 microsoft odbc 驱动程序管理器
- 5Windows与Mac远程连接的最优实践_win可以使用rdp远程mac吗
- 6jeecgboot环境搭建流程以及存在的问题_启动失败: 检查到当前菜单表是vue3版本,导致菜单加载异常,请切换到vue2版菜单!参
- 7原生微信小程序踩坑(二)------单击事件的传参问题_原生小程序全埋点用户点击
- 8计算机网络实验(Wireshark 抓包工具使用、WinPcap 编程、协议分析&流量统计程序的编写)_通过学习winpcap架构,编写一个网络抓包程序。
- 9Windows软件UI自动化测试之UiAutomation
- 10测试服务器最大内存带宽的实验
算法新手(一)——位运算、算法是什么、介绍位运算和简单排序
赞
踩
一、二进制、位运算
java中int最大值,2的31次方-1,为什么不是2的32次方-1?
——因为第一位是符号位,0表示正数,1表示复数;
1.1 Integer二进制
-1的二进制:
11111111111111111111111111111111
Integer.Min的二进制:
10000000000000000000000000000000
为什么?
规则:符号位是1,表示负数,剩下的位数全部要取反。
1.2 java int 二进制负数 为什么取反?
在Java中,int是一个32位的整数,其中一个二进制位是符号位(0代表正数,1代表负数)。如果你对一个负数取反,实际上是对其负值加1。这是因为取反操作是对整数的二进制表示进行按位取反操作,不考虑符号位。当你对一个负数取反时,符号位也会被取反,导致得到一个非常大的正数,这个数等于该负数的绝对值减1。例如,对于负数-5(二进制表示为1111 1111 1111 1111 1111 1111 1111 1011),取反操作会得到一个正数(二进制表示为0000 0000 0000 0000 0000 0000 0000 0101),这个数等于-5的绝对值(5)减1(4)。如果你需要对一个负数进行按位取反,然后再恢复原来的值,你可以先对数字取绝对值,然后对结果加1,进行按位取反操作,最后如果需要的话再转换回原来的符号。
示例代码:
int number = -5; // 假设是一个负数
int absoluteValue = number < 0 ? -number + 1 : number;
int inverted = ~absoluteValue;
// 现在inverted是按位取反后的结果
// 如果需要转换回原来的负数
int originalNegative = -inverted;
- 1
- 2
- 3
- 4
- 5
- 6
拓展阅读:
负数取反java 负数取反符号位变吗
1.3 负数为什么要取反+1?
+、-、#、/、%,等运算,在计算机系统中,都不是十进制的,所有的这些算术符号,在底层都是用二进制的位运算实现的。
位运算有哪些?
- | 或
- & 与
- ^ 异或
- ~ 取反
- >> 带符号右移
- >>> 不带符号右移
- << 带符号左移
- <<< 不带符号左移
为什么这么设计?
原因:为了让计算机在运算的时候,走一套逻辑,而不用走正数一套逻辑,负数一套逻辑;都是 取反+1;
底层的东西,效率非常重要,越底层应该越高效;
1.4 负数的两种表示方式
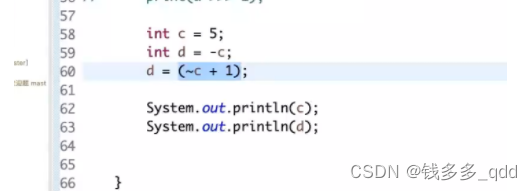
1.5 那么问题来了,int最小的负数,取反+1是多少?
——一开始我猜的是0;
实际跑出来是多少,看下图:
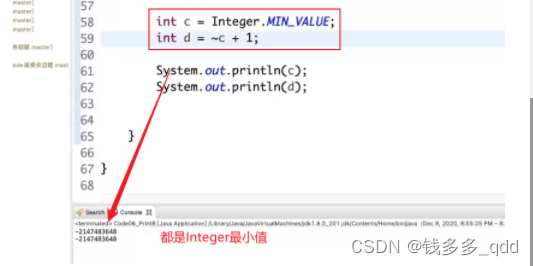
结论:还是它自己,用取反+1,可以算出来,它还是自己。
另:0取反之后还是它自己!
0: 0000 …… 0000
取反 1111 …… 1111
+1: 每一位都要进一,最后溢出了,溢出了就不要了,所以:
0000 …… 0000
二、什么是算法
三、实现打印一个整数的二进制
public static void print(int num) {
for (int i = 31; i >= 0; i--) {
System.out.print((num & (1 << i)) == 0 ? "0" : "1");
}
System.out.println();
}
- 1
- 2
- 3
- 4
- 5
- 6
public static void main(String[] args) { // 32位 // int num = -1; // // print(num); // // // int test = 1123123; // print(test); // print(test<<1); // print(test<<2); // print(test<<8); // // // int a = Integer.MAX_VALUE; // System.out.println(a); print(-1); int a = Integer.MIN_VALUE; print(a); // int b = 123823138; // int c = ~b; // print(b); // print(c); // print(-5); // System.out.println(Integer.MIN_VALUE); // System.out.println(Integer.MAX_VALUE); // int a = 12319283; // int b = 3819283; // print(a); // print(b); // System.out.println("============="); // print(a | b); // print(a & b); // print(a ^ b); // int a = Integer.MIN_VALUE; // print(a); // print(a >> 1); // print(a >>> 1); // // int c = Integer.MIN_VALUE; // int d = -c ; // // print(c); // print(d); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
四、给定一个参数N,返回1!+2!+3!+4!+…+N!的结果
public class Code02_SumOfFactorial { public static long f1(int N) { long ans = 0; for (int i = 1; i <= N; i++) { ans += factorial(i); } return ans; } public static long factorial(int N) { long ans = 1; for (int i = 1; i <= N; i++) { ans *= i; } return ans; } public static long f2(int N) { long ans = 0; long cur = 1; for (int i = 1; i <= N; i++) { cur = cur * i; ans += cur; } return ans; } public static void main(String[] args) { int N = 10; System.out.println(f1(N)); System.out.println(f2(N)); } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
五、冒泡、选择、插入排序
5.1 冒泡排序
冒泡排序(Bubble Sort)是一种简单的排序算法,它的基本思想是通过不断交换相邻两个元素的位置,使得较大的元素逐渐往后移动,直到最后一个元素为止。冒泡排序的时间复杂度为 O ( n 2 ) O(n^2)O(n 2 ),空间复杂度为 O ( 1 ) O(1)O(1),是一种稳定的排序算法。
其实现过程可以概括为以下几个步骤:
- 从序列的第一个元素开始,对相邻的两个元素进行比较,如果它们的顺序错误就交换它们的位置,即将较大的元素往后移动,直到遍历到序列的最后一个元素;
- 对剩下的元素重复上述步骤,直到整个序列都已经有序;

5.1.1 代码实现
public class Code05_BubbleSort { public static void bubbleSort(int[] arr) { if (arr == null || arr.length < 2) { return; } for (int end = arr.length - 1; end > 0; end--) { for (int i = 0; i < end; i++) { if (arr[i] > arr[i + 1]) { swap(arr, i, i + 1); } } } } // 交换arr的i和j位置上的值 public static void swap(int[] arr, int i, int j) { int tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
5.1.2 冒泡排序的应用场景
冒泡排序虽然时间复杂度较高,但是它的实现简单,容易理解,并且在某些特定场景下仍然有着广泛的应用。以下是一些冒泡排序的应用场景:
- 数据量较小的排序:当待排序的数据量较小时,冒泡排序的效率并不比其他排序算法低,甚至在某些情况下可能更优;
- 数据基本有序的排序:当待排序的数据基本有序时,冒泡排序的效率比其他排序算法更高。因为冒泡排序可以在一轮遍历中将已经有序的元素排除在外,从而减少比较和交换的次数;
- 学习排序算法:冒泡排序是最基本的排序算法之一,它的实现简单,容易理解,是学习排序算法的入门算法;
需要注意的是,如果待排序的数据量较大,或者数据分布比较随机,冒泡排序的效率会比较低,不如其他排序算法。因此,在实际应用中,需要根据具体的情况选择适合的排序算法。
5.1.3 冒泡排序在spring 中的应用
在 Spring 框架中,冒泡排序算法并没有直接应用到核心模块中,但是它可以作为一种排序算法被使用在 Spring 的某些模块中,例如:
- Spring Security 模块中的权限排序:Spring Security 是一个基于 Spring 的安全框架,它提供了一套完整的安全解决方案,包括认证、授权、攻击防护等功能。在 Spring Security 中,权限可以通过冒泡排序算法来进行排序,以便于在授权时按照顺序进行匹配;
- Spring Batch 模块中的数据排序:Spring Batch 是一个基于 Spring 的批处理框架,它可以帮助用户快速构建和执行大规模、复杂的批处理作业。在 Spring Batch 中,数据排序是一个常见的操作,可以使用冒泡排序算法来实现;
需要注意的是,冒泡排序算法虽然简单,但是在实际应用中效率较低,因此在处理大规模数据时不建议使用。在 Spring 框架中,如果需要进行排序操作,建议使用更高效的排序算法,例如快速排序、归并排序等。
5.2 选择排序
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理是:第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法。(引用于百度百科)
选择排序的具体实现过程如下:
- 遍历待排序序列,找到其中最小的元素,并记录其下标;
- 将最小的元素与序列的第一个元素交换位置;
- 在剩余的元素中继续遍历,找到其中最小的元素,并记录其下标;
- 将最小的元素与序列的第二个元素交换位置;
- 重复步骤 3 和 4,直到整个序列有序为止。
选择排序的时间复杂度为 O(n^2),其中 n 是待排序序列的长度。虽然选择排序的时间复杂度较高,但是它的实现简单,容易理解,并且在某些特定场景下仍然有着广泛的应用。需要注意的是,选择排序是一种不稳定的排序算法,即相等的元素在排序前后的相对位置可能会发生改变。
5.2.1 代码实现
public class Code04_SelectionSort { public static void selectionSort(int[] arr) { if (arr == null || arr.length < 2) { return; } for (int i = 0; i < arr.length - 1; i++) { int minIndex = i; for (int j = i + 1; j < arr.length; j++) { if(arr[j] < arr[minIndex]) { minIndex = j; } } swap(arr, i, minIndex); } } public static void swap(int[] arr, int i, int j) { int tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp; } // for test public static void comparator(int[] arr) { Arrays.sort(arr); } // for test public static int[] generateRandomArray(int maxSize, int maxValue) { // Math.random() [0,1) // Math.random() * N [0,N) // (int)(Math.random() * N) [0, N-1] int[] arr = new int[(int) ((maxSize + 1) * Math.random())]; for (int i = 0; i < arr.length; i++) { // [-? , +?] arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random()); } return arr; } // for test public static int[] copyArray(int[] arr) { if (arr == null) { return null; } int[] res = new int[arr.length]; for (int i = 0; i < arr.length; i++) { res[i] = arr[i]; } return res; } // for test public static boolean isEqual(int[] arr1, int[] arr2) { if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) { return false; } if (arr1 == null && arr2 == null) { return true; } if (arr1.length != arr2.length) { return false; } for (int i = 0; i < arr1.length; i++) { if (arr1[i] != arr2[i]) { return false; } } return true; } // for test public static void printArray(int[] arr) { if (arr == null) { return; } for (int i = 0; i < arr.length; i++) { System.out.print(arr[i] + " "); } System.out.println(); } // for test public static void main(String[] args) { int testTime = 500000; int maxSize = 100; int maxValue = 100; boolean succeed = true; for (int i = 0; i < testTime; i++) { int[] arr1 = generateRandomArray(maxSize, maxValue); int[] arr2 = copyArray(arr1); selectionSort(arr1); comparator(arr2); if (!isEqual(arr1, arr2)) { succeed = false; printArray(arr1); printArray(arr2); break; } } System.out.println(succeed ? "Nice!" : "Fucking fucked!"); int[] arr = generateRandomArray(maxSize, maxValue); printArray(arr); selectionSort(arr); printArray(arr); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
5.3.2 选择排序的应用场景
选择排序虽然时间复杂度较高,但是它的实现简单,容易理解,并且在某些特定场景下仍然有着广泛的应用。以下是一些适合使用选择排序的场景:
- 数据量较小:当待排序序列的数据量较小时,选择排序的效率还是比较高的。在这种情况下,选择排序比其他高级排序算法(如快速排序、归并排序等)更容易实现和理解;
- 内存限制:选择排序是一种原地排序算法,即不需要额外的内存空间来存储临时变量。因此,当内存空间有限时,选择排序是一种比较合适的排序算法;
- 部分有序:当待排序序列已经有一部分有序时,选择排序的效率会比其他排序算法高。这是因为选择排序每次只选择最小的元素进行交换,因此不会破坏已经有序的部分;
需要注意的是,选择排序的时间复杂度较高,因此在处理大规模数据时,应该使用其他更高效的排序算法。
5.3.3 选择排序在spring 中的应用
在 Spring 中,选择排序并不是一个常用的算法,因此它并没有被直接应用在 Spring 框架中。然而,选择排序的思想可以启发我们在 Spring 中的一些实践,例如:
- Bean 的排序:在 Spring 中,我们可以通过实现 org.springframework.core.Ordered 接口或者使用 @Order 注解来控制 Bean 的加载顺序。这种方式类似于选择排序中的选择最小元素,即通过指定 Bean 的优先级来控制其加载顺序;
- AOP 切面的优先级:在 Spring AOP 中,我们可以通过 org.springframework.core.annotation.Order 注解来控制切面的优先级。这种方式也类似于选择排序中的选择最小元素,即通过指定切面的优先级来控制其执行顺序;
- Spring Security 中的 Filter 链:在 Spring Security 中,Filter 链是一种类似于责任链模式的机制,它由多个 Filter 组成,每个 Filter 负责不同的安全检查。这种方式也类似于选择排序中的选择最小元素,即通过指定 Filter 的执行顺序来控制安全检查的顺序;
虽然选择排序并不是 Spring 中的常用算法,但是它的思想可以启发我们在 Spring 中的一些实践,从而提高代码的可读性和可维护性。
5.3 插入排序
插入排序(Insertion Sort)是一种简单直观的排序算法,它的基本思想是将待排序序列分为已排序区间和未排序区间,然后每次从未排序区间取出一个元素,将其插入到已排序区间的合适位置中,使得插入后仍然保持已排序区间有序。重复这个过程,直到未排序区间为空,整个序列有序为止。
具体来说,插入排序的实现可以分为两个步骤:
- 将待排序序列分为已排序区间和未排序区间。初始时,已排序区间只包含第一个元素,而未排序区间包含剩余的所有元素;
- 从未排序区间取出一个元素,将其插入到已排序区间的合适位置中。插入时,我们从已排序区间的末尾开始比较,找到插入位置后将其插入,并将已排序区间的元素向后移动一位。
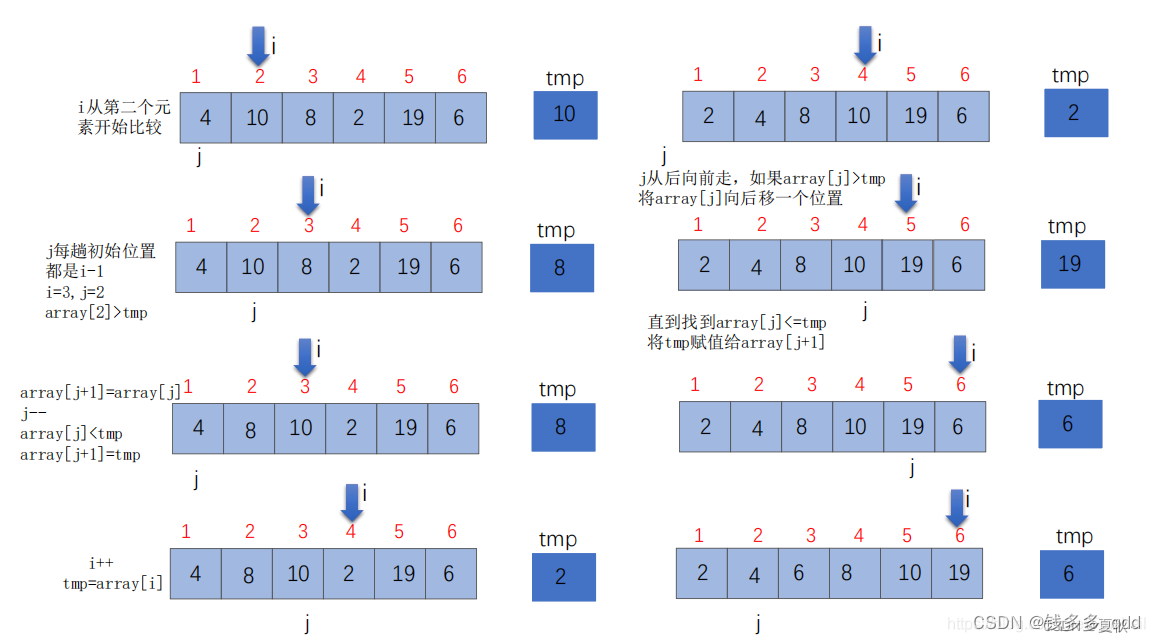
5.3.1 代码实现
public static void insertionSort(int[] arr) { if (arr == null || arr.length < 2) { return; } for (int i = 1; i < arr.length; i++) { // 0 ~ i 做到有序 for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) { swap(arr, j, j + 1); } } } // i和j,数交换 public static void swap(int[] arr, int i, int j) { int tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
5.3.2 插入排序的应用场景
插入排序适用于以下场景:
- 数据规模较小:插入排序的时间复杂度为 O(n^2),对于数据规模较小的排序任务,插入排序的效率较高;
- 数据基本有序:当待排序序列基本有序时,插入排序的时间复杂度可以达到 O(n),即最优情况下的时间复杂度,因此插入排序在这种情况下的效率非常高;
- 辅助排序算法:插入排序通常用作其他排序算法的辅助排序算法,例如快速排序的子过程;
- 链表排序:插入排序是一种适用于链表的排序算法,因为链表的节点可以通过指针直接插入到已排序链表的合适位置中,从而避免了数组排序时的元素移动操作;
插入排序适用于数据规模较小、数据基本有序、辅助排序算法和链表排序等场景,但对于大规模数据排序,效率较低,因此在实际应用中需要根据具体情况选择合适的排序算法。
5.3.3 插入排序在spring 中的应用
在 Spring 框架中,插入排序主要用于 BeanFactory 的初始化工作中,即对 BeanDefinitionMap 中的 BeanDefinition 进行排序。
在 Spring 中,BeanDefinitionMap 是一个 Map 类型的数据结构,其中包含了所有的 BeanDefinition。当 Spring 容器启动时,需要对 BeanDefinition 进行排序,以便在后续的 Bean 实例化过程中能够正确地解析依赖关系。
为了实现 BeanDefinition 的排序,Spring 使用了插入排序算法。具体来说,Spring 使用了一个名为 SimpleAliasRegistry 的类来管理 BeanDefinition,其中包含了一个名为 singletonObjects 的 Map,用于存储已经实例化的单例 Bean。在初始化 BeanFactory 时,Spring 会对 BeanDefinition 进行排序,并按照排序后的顺序依次实例化 Bean,并将其存储到 singletonObjects 中。
以下是 Spring 中插入排序的示例代码:
public class SimpleAliasRegistry implements AliasRegistry { private final Map<String, String> aliasMap = new ConcurrentHashMap<>(16); private final Map<String, Object> singletonObjects = new ConcurrentHashMap<>(256); private final Map<String, Object> earlySingletonObjects = new HashMap<>(16); private final Map<String, ObjectFactory<?>> singletonFactories = new HashMap<>(16); private final Set<String> registeredSingletons = new LinkedHashSet<>(256); private final List<String> singletonCurrentlyInCreation = new ArrayList<>(16); private volatile boolean singletonsCurrentlyInDestruction = false; private final Map<String, BeanDefinition> beanDefinitionMap = new ConcurrentHashMap<>(256); // ... public void registerBeanDefinition(String beanName, BeanDefinition beanDefinition) { this.beanDefinitionMap.put(beanName, beanDefinition); this.frozenBeanDefinitionNames = null; } public void preInstantiateSingletons() throws BeansException { List<String> beanNames = new ArrayList<>(this.beanDefinitionMap.keySet()); // 对 BeanDefinition 进行排序 Collections.sort(beanNames, new Comparator<String>() { @Override public int compare(String beanName1, String beanName2) { return getPriority(beanName1) - getPriority(beanName2); } }); // 依次实例化 Bean for (String beanName : beanNames) { BeanDefinition bd = this.beanDefinitionMap.get(beanName); if (bd.isSingleton()) { if (bd.isLazyInit()) { this.registerLazyInit(beanName, bd); } else { this.getBean(beanName); } } } } // ... }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49




