pytorch入门：选择合适的激活函数，损失函数，优化器_lstm模型中的优化器和损失函数作用

选择合适的激活函数

激活函数主要作用就是给神经网络提供非线性建模能力。如果没有激活函数，神经网络就只能处理线性可分问题

神经网络的选择，如果网络层数不多，选择 sigmoid ,tanh, relu ,sofmax 都可以，如果网络层次较多，就要防止梯度消失的问题，就不能选sigmoid tanh 了，因为他们的导数都小于1，多层叠加后就会变得很小。所以层数较多的激活函数需要考虑其导数不易小于1， 也不能大于1.。。大于1 会导致梯度爆炸，所以导数为1 是最好的。这就是 relu 了，虽然很简单但也是划时代的。

m = nn.Sigmoid()
input = torch.randn(2)
output = m(input)
1
2
3

选择合适的损失函数

训练模型的过程实际就是优化损失函数的过程，损失函数对每个参数的偏导就是梯度下降中提到的梯度。防止过拟合就是给损失函数添加正则项，损失函数用来衡量模型的好坏，损失越小说明模型和参数越符合训练样本。任何衡量模型预测值和真实值之间的差异的函数都可以交损失函数。

机器学习中常用 交叉嫡（Cross Entropy) 和均方误差（MSE ），对应分类问题和回归问题。

分类问题一般使用交叉嫡，反应的是两个概率分布的距离（不是欧式距离），回归问题预测的是任意一个实数，反应的预测值和真实值之间的距离就可以使用欧氏距离来表示，使用均方差为损失函数。

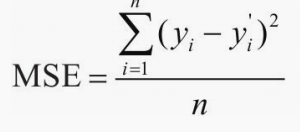
pytorch 集成了很多损失函数，介绍两种，其他的基本都是从他们的基础上的延申或变种。

1. torch.nn.MSELoss torch.nn.MSELoss(size_average = None, reduce=None, reduction='mean') 计算公式：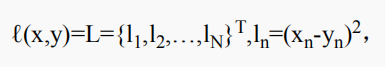
   N 是批量大小，reduction = ‘mean’ ，l(x,y) = mean(L )， reduction = ‘sum’ ，l(x,y) = sum(L).。x,y 为任意形式的张量，每个张量n 个元素。reduciton = sum ，只是差平方和，不除以n。size_average ，reduce 不用，他们的取值会覆盖 reduction

torch.manual_seed(10)
loss = nn.MSELoss(reduction='mean')
input = torch.randn(1,2,requires_grad = True)
print(input)
target = torch.randn(1,2)
print(target)
output = loss(input,target)
print(output)
output.backward()
>>>
>tensor([[-0.6014, -1.0122]], requires_grad=True)
tensor([[-0.3023, -1.2277]])
tensor(0.0680, grad_fn=<MseLossBackward>)
1
2
3
4
5
6
7
8
9
10
11
12
13

2. torch.nn.CrossEntropyLoss ，又称对数拟然损失，或逻辑回归损失（Logistic loss)，pytroch中是将input 经过softmax激活函数，将向量归一化为概率的i形式，在于target 计算严格的交叉嫡损失。多分类中采用 softmax 加 交叉嫡损失函数。

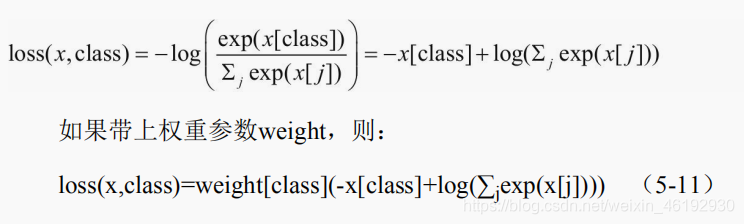
这个weight（tensor) ，给每个类别的loss 设置值，用于类别不均衡的问题，必须是 float 类型的tensor ，长度与类别C 一致，就是每个类别都要设置一个权重，。

torch.nn.CrossEntroyLoss(weight=None,size_average=None,ignore_index=-100, reduce = None,reduction='mean')

loss = nn.CrossEntroyLoss()
input = torch.randn(3,5,requires_grad=True)     # 设置五个类别
target = torch.empty(3,dtype = torch.long).random_(5)
output = loss(input,target)
output.backward()
1
2
3
4
5
6
7

选择合适的优化器

同一个模型因为选择的优化器不同性能可能差距很大。甚至导致一些模型无法训练

传统梯度优化器的不足

传统梯度更新算法基本思想就是，设定一个学习率λ， 参数沿梯度的反方向移动，更新策略为 : θ <-- θ - λ* g 。当学习率选择恰当就可以收敛到全面最优点或局部最优点。

不足就是对超参数 学习率敏感（过小收敛慢，过大可能会越过极值点）。有时还会因为再迭代过程中抱持不变，很容易造成算法卡在鞍点的位置

在平坦的区域也会因为梯度接近零，发生误判，让迭代提取结束。所以改善的方向就是：1. 梯度方向（动量更新策略） ，2 . 学习率（调参问题），3. 双管齐下，自适应更新策略

动量算法

动量（Momentum）是模拟物理里动量的概念，一个物体再运动时具有惯性，将这个思想用到了梯度下降中，可以增加算法的收敛速度和稳定性。

动量算法每一步下降都有由前面下降方向的一个累积和当前点的梯度方向组合而成。伪代码：

每一步都要两个梯度方向（历史梯度，当前梯度）合并再下降，那还可以先根据历史梯度方向再前进一步，按照前进一步的位置的超前梯度进行 合并。这样就可以再更前面的位置看见梯度，然后根据那个位置来修正这一梯度方向。这就是 动量算法的改进版本 称为 NAG 算法。 这种预更新的方法可以防止大幅度震荡，不会错过最小值，对参数更新更加敏感。

AdaGrad 算法

动量算法虽然环节了参数空间方向的问题，但学习率的控制还是不理想，所以就有了自适应优化算法，根据不同情况自动调整参数。

AdaGrad 算法是通过参数来调整学习率，可以独立的自动调整模型的学习率，对稀疏参数进行大幅度更新，对频繁参数继续小幅度更新，所以很适合用来处理稀疏数据。

1. 随着迭代时间加长，累计梯度变大，导致学习速率 Δθ变小，接近目标值时，不会因为学习率过大跳过极值点
2. 不同参数之间的学习率不同，因此不容易再鞍点卡住。
3. 梯度积累参数较小，学习率就较大，所以参数迭代的步长就越大，
4. 由于累计梯度平方导致学习率过早或过量减少，这是这个算法的不足。

RMSProp 算法

这个是通过修改 AdaGrad 得来，目的是再非凸背景下效果更好。针对梯度平方和累计越来越大的问，RMSProp 指数加权和的移动平均代题梯度平方和。引入了新的超参数 ρ ，控制移动平均的长度范围

Adam 算法

这个本质上是带动量的 RMSprop ，利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。优的就是经过偏执矫正后，每一次迭代学习率都有个确定范围，让参数更加平稳。

看懂不，，就知道好用就行。

有时可以综合考虑使用这些优化算法，比如采用 Adam ，大大节省训练时间，也不用担心初始化和参数调整，获得较好的参数后，在采用SG + 动量优化，达到最佳性能。实际上迭代次数超过 150 后，SGD 的效果是优于Adam的。