希尔伯特第 13 问题，Kolmogorov–Arnold representation theorem 和通用近似定理（Universal approximation theorem）_kolmogorov-arnold representation theorem

---

深度学习并不像你想象的那么令人印象深刻，因为它仅仅是通过曲线拟合产生的插值结果。但在高维空间中，不存在插值这样的情况。在高维空间中，一切都是外推。
——Yann LeCun

1. 希尔伯特第十三问题

希尔伯特第十三个问题（Hilbert’s thirteenth problem）是 23 个希尔伯特问题之一，该问题列于 David Hilbert 于 1900 年编制的著名列表中。它需要使用两个参数的代数（变体（variant）：连续）函数证明是否存在所有 7 次方程的解。它首先出现在列线图（nomography）的背景下，特别是“列线图构造”——一个使用两个变量的函数构造多个变量的函数的过程。1957 年，Vladimir Arnold 在证明 Kolmogorov–Arnold representation theorem 时肯定地解决了连续函数的变体，但代数函数的变体仍未解决。

1.1 介绍

William Rowan Hamilton 于 1836 年表明，每个七次方程都可以通过根式化简为以下形式：

$$x^7+a{x}^3+b{x}^2+cx+1=0。$$

关于这个方程，希尔伯特问它的解 $x$，作为三个变量 $a$、$b$ 和 $c$ 的函数，是否可以表示为有限数量的二元函数的组合。

1.2 历史

希尔伯特最初提出了他的代数函数（algebraic functions）问题（Hilbert 1927, “…Existenz von algebraischen Funktionen…”, i.e., “…existence of algebraic functions…”; also see Abhyankar 1997, Vitushkin 2004）。然而，希尔伯特在这个问题的后来版本中也询问了连续函数类（class of continuous functions）是否有解。

问题的第二个（“连续”）变体的主要是以下问题：
每个三变量连续函数能否表示为有限个两个变量的连续函数的组合？1957 年，Vladimir Arnold 对这个一般性问题给出了肯定的回答，当时他只有 19 岁，是 Andrey Kolmogorov 的学生。Kolmogorov 在前一年表明，任何多变量函数都可以用有限数量的三变量函数构造。然后阿诺德扩展了这项工作，表明实际上只需要双变量函数，从而回答了希尔伯特在连续函数类中提出的问题。之后阿诺尔德和日本数学家志村五郎发表了一篇论文（Superposition of algebraic functions (1976), in Mathematical Developments Arising From Hilbert’s Problems），一起回到了问题的代数版本。这些结果后来被进一步发展，推导出人工神经网络中的通用近似定理，指人工神经网络能近似任意连续函数。

1.2.1 近期发展

“数学的难点在于你有 90% 的时间会失败，而你必须是那种可以在 90% 的时间失败的人，”Farb 曾在一次晚宴上说。 当另一位客人，也是一位数学家，对他有 10% 的成功率表示惊讶时，他很快承认，“不不不，我在夸大我的成功率。 好极了。

图 Benson Farb。

Farb 是芝加哥大学的拓扑学家，他对自己最近的失败感到非常高兴——不过，公平地说，这不是他一个人的事。它围绕着一个问题展开，奇怪的是，这个问题既已解决又未解决，既封闭又开放。

这个问题是 23 个当时未解决的数学问题中的第 13 个，德国数学家大卫·希尔伯特在 20 世纪之交预测这些问题将塑造该领域的未来。该问题询问有关求解七次多项式方程的问题。术语“多项式（polynomial）”是指一串数学项——每个项都由数值系数和变量的幂组成——通过加法和减法连接。“7 次（Seventh-degree）”表示字符串中最大的指数是 7。

一个被称为希尔伯特第 13 个问题的已有数十年历史的问题被认为非常重要，它将影响数学领域。尽管它长期以来一直被认为已经解决，但新的研究表明它仍然需要继续研究。

数学家们已经有了巧妙而有效的方法来求解二阶、三阶和一定程度的四阶方程。这些公式——就像我们熟悉的二次方程式一样——涉及代数运算，仅意味着算术和根式（例如，平方根）。但指数越高，方程就越棘手，求解它几乎是不可能的。希尔伯特第 13 个问题询问是否可以使用加、减、乘、除的组合加上两个变量的代数函数来求解七次方程。

答案可能是否定的。但对 Farb 来说，问题不仅仅是求解复杂类型的代数方程。希尔伯特的第 13 个问题是数学中最基本的开放问题之一，他说，因为它引发了深刻的问题：多项式有多复杂，我们如何衡量它？ “为了理解多项式的根，发明了大量现代数学，”法布说。

图 1900 年，大卫希尔伯特列出了 23 个重要的未解决问题。从某种意义上说，第 13 个问题既是已解决的也是未解决的。

这个问题让他和加州大学欧文分校的数学家 Jesse Wolfson 陷入了一个数学兔子洞，他们仍在探索其中的隧道。他们还聘请了哈佛大学的数论学家、Farb 的老朋友 Mark Kisin 来帮助他们进行挖掘。

图 数学兔子洞。

Farb 承认，他们仍然没有解决希尔伯特的第 13 个问题，而且可能还差得远。但他们发掘了实际上已经消失的数学策略，并探索了这个问题与多个领域之间的联系，包括复分析、拓扑学、数论、表示论和代数几何。在这样做的过程中，他们取得了自己的进展，尤其是在将多项式与几何联系起来以及缩小希尔伯特问题的可能答案范围方面。他们的工作还提出了一种使用复杂性度量对多项式进行分类的方法——类似于与未解决的 P 与 NP 问题相关的复杂性类别。

佐治亚大学的数学家 Daniel Litt 说：“他们真的成功地从问题中提取了一个比之前研究的版本更有趣的版本”。“他们让数学界意识到许多自然而有趣的问题。”

1.2.1.1 打开和关闭，然后再打开

许多数学家已经认为问题已经解决了。 那是因为一位名叫 Vladimir Arnold 的苏联神童和他的导师 Andrey Nikolyevich Kolmogorov 在 1950 年代后期发表了它的证明，7 次方程的解可以简化为两个变量的连续函数的叠加。

图 1957年的 Vladimir Arnold。

对于大多数数学家来说，Arnold-Kolmogorov 的工作结束了这本书。甚至维基百科——不是权威来源，而是公众知识的合理代理——直到最近才宣布此案结案。

图 虽然 Vladimir Arnold 和他的导师 Andrey Nikolyevich Kolmogorov 在 1950 年代证明了 Hilbert 第 13 个问题的一个版本，但它可能不是 Hilbert 感兴趣的变体。

但五年前，Farb 在 Arnold 的一篇文章中看到了一些引人入胜的语句，这位著名数学家在文中回顾了他的工作和职业。Farb 惊讶地发现 Arnold 将 Hilbert 的第 13 个问题描述为开放的，并且实际上花了 40 年的时间试图解决他本应已经攻克的问题。

“所有这些论文都只是重复说它已经解决了。他们显然不了解实际问题，”Farb 说。他已经与 Wolfson（当时是博士后研究员）在一个拓扑项目上合作，当他分享他在 Arnold 论文中的发现时，Wolfson 插了进来。2017 年，在庆祝 Farb 50 岁生日的研讨会上，Kisin 听了 Wolfson 的演讲，并惊讶地意识到他们关于多项式的想法与他自己的数论工作中的问题有关。他加入了合作。

问题混乱的原因很快就清楚了：Kolmogorov 和 Arnold 只解决了问题的一个变体。他们的解决方案涉及数学家所说的连续函数，即没有突然中断（discontinuities）或尖点（cusps）的函数。它们包括熟悉的运算，如正弦、余弦和指数函数，以及更奇特的运算。

但研究人员不同意希尔伯特是否对这种方法感兴趣。“许多数学家认为希尔伯特真正指的是代数函数，而不是连续函数，”不列颠哥伦比亚大学的数学家 Zinovy Reichstein 说。Farb 和 Wolfson 一直在研究他们认为 Hilbert 自发现以来就打算解决的问题。

Farb 说，希尔伯特第 13 个问题是一个万花筒。“你打开这个东西，你投入的越多，你得到的新方向和想法就越多，”他说。“它打开了通往整个阵列（array）的大门，这整个美丽的数学网络。”

1.2.1.2 事情的根源

自数学出现以来，数学家就一直在探索多项式。3000 多年前雕刻的石碑表明，古代巴比伦数学家使用一个公式来求解二次多项式——代数学生今天学习的二次方程式的楔形文字先驱。该公式：

$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$

告诉您如何找到二次多项式：

$$a{x}^2+bx+c=0$$

的根或使表达式等于零的 $x$ 值。

随着时间的推移，数学家们自然而然地想知道是否存在适用于更高次多项式的这种干净的公式。“这个问题的千年历史就是要回到强大、简单和有效的东西上，”Wolfson 说。

多项式的阶数越高，它们变得越笨重。在 1545 年的著作“Ars Magna” 中，意大利博学家 Gerolamo Cardano 发表了用于求三次和四次多项式的根的公式。

可以使用以下公式求出三次多项式：

$$a{x}^3+b{x}^2+cx+d=0$$

的根：

x = ( − b 3 27 a 3 + b c 6 a 2 − d 2 a ) + ( − b 3 27 a 3 + b c 6 a 2 − d 2 a ) 2 + ( c 3 a − b 2 9 a 2 ) 3 3 + ( − b 3 27 a 3 + b c 6 a 2 − d 2 a ) − ( − b 3 27 a 3 + b c 6 a 2 − d 2 a ) 2 + ( c 3 a − b 2 9 a 2 ) 3 − b 3 a 3

$$\begin{aligned} x=&\sqrt[3]{\left(\frac{-b^{3}}{27a^{3}}+\frac{bc}{6a^{2}}-\frac{d}{2a}\right)+\sqrt{\left(\frac{-b^{3}}{27a^{3}}+\frac{bc}{6a^{2}}-\frac{d}{2a}\right)^{2}+\left(\frac{c}{3a}-\frac{b^{2}}{9a^{2}}\right)^{3}}}\\ &+\sqrt[3]{\left(\frac{-b^{3}}{27a^{3}}+\frac{bc}{6a^{2}}-\frac{d}{2a}\right)-\sqrt{\left(\frac{-b^{3}}{27a^{3}}+\frac{bc}{6a^{2}}-\frac{d}{2a}\right)^{2}+\left(\frac{c}{3a}-\frac{b^{2}}{9a^{2}}\right)^{3}}-\frac{b}{3a}} \end{aligned}$$ x=​3(27a3−b3​+6a2bc​−2ad​)+(27a3−b3​+6a2bc​−2ad​)2+(3ac​−9a2b2​)3 ​ ​+3(27a3−b3​+6a2bc​−2ad​)−(27a3−b3​+6a2bc​−2ad​)2+(3ac​−9a2b2​)3 ​−3ab​ ​​

四次公式更糟。随着方程次数的增加，求根公式的复杂度也急剧增加。那么我们有没有可能写出 4 次、5 次、6 次乃至 7 次方程的求根公式？

Abel–Ruffini theorem 告诉我们，5 次以及更高次的多项式方程，并不存在“一般意义”的求根公式。这个所谓的“一般”在数学上有严格定义，就是只包含只能包含加减乘除以及乘方、开方 6 种运算。所以七次方程的“一般”求根公式显然也是不存在的。而希尔伯特所说的求根公式，比“一般”要宽松一些。

经过一系列变换后，7 次方程可以简化为如下的形式：

$$x^7+a{x}^3+b{x}^2+cx+1=0$$

其中 $a$、$b$、$c$ 都是复数，方程的解应该是 $a$、$b$、$c$ 的函数，即 $x=f(a,b,c)$。希尔伯特的意思是：

这个三元变量函数能否能表示为二元变量函数的组合？

“随着次数的提高，他们的复杂性也随之提高；它们形成了一座复杂的塔，”哈佛大学的 Curt McMullen 说。“我们怎样才能捕捉到那座复杂的塔？”

意大利数学家 Paolo Ruffini 在 1799 年提出，5 次或更高次的多项式无法使用算术和根式求解；挪威人 Niels Henrik Abel 于 1824 年证明了这一点。换句话说，不可能有类似的“五次公式”。幸运的是，出现了其他想法，为更高次多项式提出了前进方向，可以通过替换来简化。例如，在 1786 年，一位名叫 Erland Bring 的瑞典律师表明，形式为：

$$a{x}^5+b{x}^4+c{x}^3+d{x}^2+ex+f=0$$

的任何五次多项式方程都可以重组为：

$$p{x}^5+qx+1=0$$

其中 $p$ 和 $q$ 是由 $a$、$b$、$c$、$d$、$e4 和 $f$ 确定的复数。这指出了处理多项式固有但隐藏的规则的新方法。

在 19 世纪，William Rowan Hamilton 接手了布林 Bring 和其他人离开的地方。他证明，除其他外，要找到任何六次多项式方程的根，您只需要通常的算术运算、一些平方根和立方根，以及一个仅取决于两个参数的代数公式。

1975 年，哈佛大学的美国代数学家 Richard Brauer 提出了“分解度（resolvent degree）”的概念，它描述了表示某个次数的多项式所需的最少项数。（不到一年后，Arnold 和日本数论家 Goro Shimura 在另一篇论文中介绍了几乎相同的定义。）

在 Brauer 的框架中，它代表了对此类替换（substitutions）规则的首次尝试，Hilbert 的第 13 个问题询问我们七次多项式是否有可能具有小于 3 的分解度；后来，他对六次和八次多项式也做出了类似的猜想。

但这些问题也引出了一个更广泛的问题：找到任何多项式的根所需的最少参数数量是多少？

1.2.1.3 视觉思考

解决这个问题的一种自然方法是考虑多项式的样子。 多项式可以写成函数——例如 $f(x)=x^2-3x+1$——并且可以绘制该函数。然后找到根就变成了认识到函数值为 $0$ 的地方，曲线与 $x$ 轴相交。

图 曲线交于横坐标，形成零点。

更高次的多项式会产生更复杂的图形。例如，具有三个变量的三次多项式函数会产生嵌入三维空间的光滑但扭曲的表面。而且，通过知道在哪里查看这些图形，数学家可以更多地了解它们的基本多项式结构。

We haven’t been able to address this fundamental problem; that means there’s some dark area we haven’t pushed into.

—— Curt McMullen, Harvard University

因此，许多理解多项式的努力都借鉴了代数几何和拓扑学，这些数学领域关注的是当形状和图形被投影、变形、挤压、拉伸或以其他方式转换而不破坏时会发生什么。“Henri Poincaré 基本上发明了拓扑领域，他明确表示他这样做是为了理解代数函数”，Farb 说。“当时，人们真的在与这些基本联系作斗争。”

希尔伯特本人通过将几何学应用于这个问题，发现了一个特别显着的联系。当他在 1900 年列举他的问题时，数学家们已经有了一大堆减少多项式的技巧，但他们仍然没有取得进展。然而，在 1927 年，希尔伯特描述了一个新把戏。他首先确定了简化九次多项式的所有可能方法，并在其中发现了一系列特殊的三次曲面。

希尔伯特已经知道，每个光滑的立方曲面——由三次多项式定义的曲折形状——都恰好包含 27 条直线，无论它看起来多么扭曲，这些线随着多项式系数的变化而变化。他意识到，如果他知道其中一条线，他就可以简化九次多项式来找到它的根。该公式只需要四个参数；用现代术语来说，这意味着分解度最多为 4。

“希尔伯特惊人的洞察力是，可以利用这个来自完全不同世界的几何学魔法，将 [分解度] 降低到 4”Farb 说。

1.2.1.4 迈向连接网络

当 Kisin 帮助 Farb 和 Wolfson 将点点滴滴联系起来时，他们意识到希尔伯特第 13 个问题已解决的普遍假设基本上关闭了人们对分解度的几何方法的兴趣。2020 年 1 月，Wolfson 发表了一篇论文，通过将希尔伯特关于九次多项式的几何工作扩展到更一般的理论来恢复这一想法。

希尔伯特专注于三次曲面来求解一个变量的九次多项式。但是高阶多项式呢？ Wolfson 认为，要以类似的方式解决这些问题，您可以用许多变量中的那些高阶多项式形成的一些高维“超曲面”替换那个三次曲面。这些的几何形状了解较少，但在过去几十年中，数学家已经能够证明超曲面在某些情况下总是有线。

图 显示立方体表面恰好有 27 条直线的动画插图。每个光滑的立方体表面，无论多么曲折或卷曲，都恰好包含 27 条直线。希尔伯特利用这一几何事实构造了一个九次多项式的根公式。Jesse Wolfson 进一步推进了这一想法，他使用高维“超曲面（hypersurfaces）”上的直线来为更复杂的多项式创建公式。

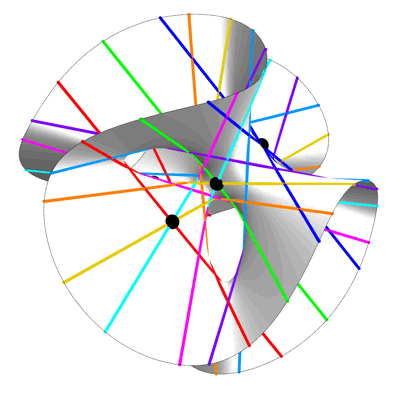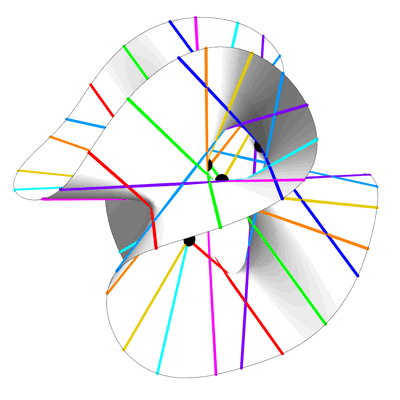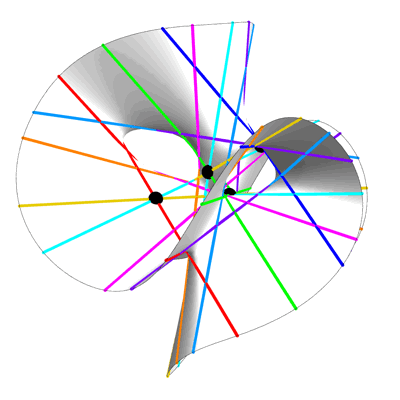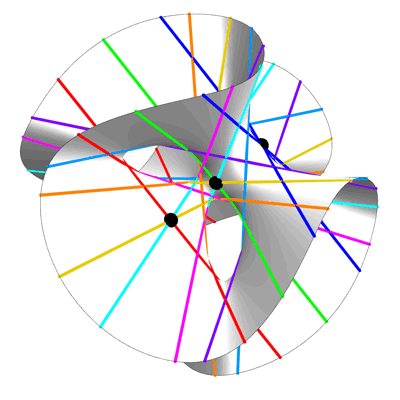
希尔伯特使用三次曲面上的直线来求解九次多项式的想法可以扩展到这些高维超曲面上的直线。Wolfson沃尔夫森使用这种方法为特定次数的多项式找到了新的、更简单的公式。这意味着即使您无法将其可视化，您也可以通过在多维三次超曲面（在本例中为 47 维）上找到一个平面来“简单地”求解 100 次多项式。

用这种新方法，Wolfson 证实了 Hilbert 的九次多项式分解次数的值。对于其他次数的多项式——尤其是次数超过 9 的多项式——他的方法缩小了分解次数的可能值。

因此，这不是对希尔伯特第 13 问题的直接攻击，而是对一般多项式的攻击。“他们找到了一些相邻的问题并在这些问题上取得了进展，其中一些是长期存在的，希望这能阐明最初的问题，”McMullen 说。他们的工作指出了思考这些数学结构的新方法。

这个分解度的一般理论也表明，希尔伯特关于六次、七次和八次方程的猜想等同于其他看似无关的数学领域的问题。Farb 说，分解度提供了一种通过一种代数复杂性对这些问题进行分类的方法，就像在复杂性类别中对优化问题进行分组一样。

尽管该理论始于希尔伯特第 13 问题，但数学家们怀疑它是否真的能解决关于七次多项式的悬而未决的问题。它以难以想象的维度讲述了巨大的、未探索的数学景观——但它在较低的数字上遇到了障碍，并且无法确定它们的解决程度。

对 McMullen 来说，尽管有这些进步迹象，但缺乏进展本身就很有趣，因为它表明这个问题隐藏着现代数学根本无法理解的秘密。“我们无法解决这个根本问题；这意味着我们还没有进入一些黑暗区域，”他说。

“解决它需要全新的想法，”Reichstein 说，他已经发展了自己的新想法，即使用他称之为本质维度（essential dimension）的概念来简化多项式。“没有办法知道他们会从哪里来。”

但三人组并没有被吓倒。“我不会放弃这个，”Farb 说。 “它肯定变成了某种白鲸。让我继续前进的是这种联系网络，以及围绕它的数学。”

1.3 列线图（Nomography）

wiki: Nomogram

2. Kolmogorov–Arnold representation theorem

在实分析和逼近理论中，Kolmogorov-Arnold 表示定理（Kolmogorov–Arnold representation theorem，或叠加定理（superposition theorem））指出，每个多元连续函数都可以表示为有限数量的单变量连续函数的两层嵌套叠加，这两个层的函数分别称为内部函数和外部函数。它解决了希尔伯特第十三问题的一个更受约束但更一般的形式。

Vladimir Arnold 和 Andrey Kolmogorov 的著作确定，如果 $f$ 是多元连续函数，则 $f$ 可以写成`有限数量的单变量连续函数的两层嵌套叠加。进一步来说，

$$f(\mathbf{x})=f(x_1,\dots ,x_n)=\sum _{q=0}^{2n}{\Phi }_q\left(\sum _{p=1}^n{\varphi }_{q,p}(x_p)\right)$$

其中 ${\Phi }_q$ 为外部函数（outer functions），${\varphi }_{q,p}$ 为内部函数（inner functions）。

从某种意义上说，他们表明唯一真正的多元函数是求和，因为所有其他函数都可以使用单变量函数和求和来编写。

2.1 历史

根据 Robert Hecht-Nielsen 在第一届神经网络会议上的说法：

The Kolmogorov theorem was discovered during a friendly mathematical duel between Kolmogorov and fellow Soviet Mathematician V.I. Arnol’d… Kolmogorov won.

Kolmogorov–Arnold 表示定理与希尔伯特第 13 问题密切相关。在 1900 年国际数学家大会上的巴黎演讲中，David Hilbert 提出了 23 个问题，他认为这些问题对数学的进一步发展很重要。这些问题中的第 13 个涉及高次一般方程的解。众所周知，对于 4 次代数方程，可以通过仅包含根和算术运算的公式计算解。 对于高阶，Galois theory 告诉我们，代数方程的解不能用基本的代数运算来表示。从所谓的 Tschirnhaus transformation 可以得出一般代数方程：

$$x^n+a_{n-1}{x}^{n-1}+\cdots +a_0=0$$

可以翻译成这样的形式：

$$y^n+b_{n-4}{y}^{n-4}+\cdots +b_{1}y+1=0$$

Tschirnhaus transformation 由仅包含根和算术运算和变换的公式给出。因此，在 $n<7$ 时，一个 $n$ 次代数方程的解可以表示为两变量函数的叠加，在 $n\ge 7$ 时，可以表示为 $n-4$ 变量函数的叠加。对于 $n=7$，解是算术运算、根、方程 $y^7+b_3{y}^3+b_2{y}^2+b_{1}y+1=0$ 解的叠加。

用代数变换进一步简化似乎是不可能的，这导致希尔伯特猜想“7 次一般方程的解不能表示为两个变量的连续函数的叠加”。这解释了希尔伯特第十三问题与将高维函数表示为低维函数叠加的关系。在此背景下，它激发了不同作者对函数论和其他相关问题的许多研究。

2.2 变体（Variants）

减少外部函数（outer functions）${\Phi }_q$ 数量的 Kolmogorov 定理的变体归功于 George Lorentz。他在 1962 年证明，外部函数 ${\Phi }_q$ 可以用单个函数 $\Phi$ 代替。更准确地说，Lorentz 证明了函数 ${\varphi }_{q,p},q=0,1,\dots ,2n,p=1,\dots ,n$ 的存在，使得：

$$f(\mathbf{x})=\sum _{q=0}^{2n}\Phi \left(\sum _{p=1}^n{\varphi }_{q,p}(x_p)\right)$$

David Sprecher 替换了内部函数 ${\varphi }_{q,p}$，通过一个单独的内部函数（inner funciton）在其参数中进行适当的转换。他证明了存在实数值 $\eta ,{\lambda }_1,\dots ,{\lambda }_n$，连续函数 $\Phi :\mathbb{R}\to \mathbb{R}$，以及实数递增连续函数 $\varphi :[0,1]\to [0,1]$，$\varphi \in \mathrm{Lip}(\ln 2/\ln (2N+2))$，$N\ge n\ge 2$，使得：

$$f(\mathbf{x})=\sum _{q=0}^{2n}\Phi \left(\sum _{p=1}^n{\lambda }_p\varphi (x_p+\eta q)+q\right)$$

Phillip A. Ostrand 将 Kolmogorov 叠加定理推广到紧致度量空间（compact metric spaces）。对于 $p=1,\dots ,m$，让 $X_p$ 是有限维 $n_p$ 的紧度量空间，让 $n={\sum }_{p=1}^m{n}_p$。则存在连续函数：

$${\varphi }_{q,p}:X_p\to [0,1],q=0,\dots ,2n,p=1,\dots ,m$$

和连续函数

$$G_q:[0,1]\to \mathbb{R},q=0,\dots ,2n$$

使得任何连续函数 $f:X_1\times \cdots \times X_m\to \mathbb{R}$ 可表示为以下形式：

$$f(x_1,\dots ,x_m)=\sum _{q=0}^{2n}{G}_q\left(\sum _{p=1}^m{\varphi }_{q,p}(x_p)\right)。$$

2.3 局限性

如此处所讨论的，该定理一般不适用于复杂的多变量函数。此外，内部函数的非平滑性和它们的“狂野行为（wild behavior）”限制了表示定理的实际使用，尽管对此存在一些争论。

3. 通用近似定理（Universal approximation theorem）

在人工神经网络的数学理论中，通用近似定理（或称万能近似定理）是在给定的感兴趣函数空间内建立算法生成的函数类密度的结果。简单说是给出了人工神经网络近似任意函数的能力。通常，这些结果涉及前馈架构（feedforward architecture）在两个欧几里得空间之间的连续函数空间上的近似能力，并且近似是关于紧凑收敛拓扑的（compact convergence topology）。

然而，在非欧几里得空间（non-Euclidean spaces）和其他常用架构之间也有各种各样的结果，更普遍的是，算法生成的函数集，例如卷积神经网络（convolutional neural network，CNN）架构，径向基函数（radial basis-functions），或具有特定属性的神经网络。大多数通用近似定理都可以分为两类。第一个量化具有任意数量的人工神经元的神经网络（“任意宽度（arbitrary width）”情况，即输入输出个数）的逼近能力，第二个侧重于具有任意数量的隐藏层的情况，每个隐藏层包含有限数量的人工神经元（“任意深度（arbitrary depth）”情况，即网络层数）。除了这两类之外，对于隐藏层数量有限且每层神经元数量有限（“深度和宽度有限”的情况）的神经网络，也有通用近似定理。

此定理意味着神经网路可以用来近似任意的复杂函数，并且可以达到任意近似精准度。但它并没有说明要如何选择神经网络参数（权重、神经元数量、神经层层数等等）来达到想近似的目标函数。

3.1 历史

George Cybenko 在 1989 年证明了单一隐藏层、任意宽度、并使用 sigmoid 激活函数作为激励函数的前馈神经网路的通用近似定理的第一个版本。Kurt Hornik、Maxwell Stinchcombe 和 Halbert White 在 1989 年表明，只有一个隐藏层的多层前馈网络是通用近似器（universal approximators）。Hornik 还在 1991 年表明，激励函数的选择不是关键，前馈神经网路的多层神经层及多层前馈架构（multilayer feed-forward architecture）才是使神经网络有成为通用逼近器的关键。Moshe Leshno 等人在 1993 年和后来的 Allan Pinkus 在 1999 年证明，通用近似性质等同于具有非多项式激活函数（nonpolynomial activation function）。

许多作者也研究了任意深度情况，例如 Gustaf Gripenberg 在 2003 年，Dmitry Yarotsky，Zhou Lu 等人在 2017 年，Boris Hanin 和 Mark Sellke 在 2018 年，以及 2020 年的 Patrick Kidger 和 Terry Lyons。2021年，Park 等人使用以 ReLU 为激活函数的前馈神经网络，得到了 $L^p$ 函数通用近似所需的最小宽度。同年，Paulo Tabuada 和 Bahman Gharesifard 使用控制理论论证也获得了可直接应用于残差神经网络（residual neural networks）的类似结果。

1999 年，Maiorov 和 Pinkus 首次研究了有界深度（bounded depth）和有界宽度（bounded width）的情况。他们表明存在一个解析 sigmoidal 激活函数，使得两个隐藏层单元数有限的隐藏层神经网络是通用近似器。使用算法和计算机编程技术，Guliyev 和 Ismailov 构建了一个平滑的 sigmoidal 激活函数，为两个隐藏层单元较少的隐藏层前馈神经网络提供了通用的近似特性。2018 年的论文建设性地证明了具有有界宽度的单隐藏层网络仍然是单变量函数的通用近似器，但该属性不再适用于多变量函数。

存在该定理的几个扩展，例如不连续激活函数（discontinuous activation functions）、非紧致域（noncompact domains）、可验证网络（certifiable networks）、随机神经网络（random neural networks）和替代网络架构和拓扑（alternative network architectures and topologies）。

量子神经网络可以用电路量子计算机的不同数学工具来表示，从量子感知器到变分量子电路，都基于量子逻辑门的组合。变分量子电路基于参数电路，不涉及神经网络。相反，量子感知器能够设计具有与前馈神经网络相同结构的量子神经网络，前提是每个节点的阈值行为不涉及量子态的崩溃，即没有测量过程。 2022 年，这种为量子神经网络提供激活函数行为的免测量构建模块已经被设计出来。量子电路返回与量子比特相关的 -1 到 +1 区间内的压缩函数的任意近似值。这种设计任意量子激活函数的方法通常可以实现量子多感知器和量子前馈神经网络。

3.2 任意宽度的情况（Arbitrary-width case）

George Cybenko 和 Kurt Hornik 等人在 80 年代——1990 年代的一系列论文中，建立了几个任意宽度和有界深度的通用近似定理。以下是最常被引用的：

通用近似定理：

让 $C(X,Y)$ 表示从 $X$ 到 $Y$ 映射的连续函数集合。令 $\sigma \in C(\mathbb{R},\mathbb{R})$。注意 $(\sigma \circ x{)}_i=\sigma (x_i)$，所以 $\sigma \circ x$ 表示 $\sigma$ 应用于 $x$ 的每个部分（component）。

然后 $\sigma$ 不是多项式，当且仅当对于每个 $n\in \mathbb{N}$，$m\in \mathbb{N}$，紧致（compact）$K\subseteq {\mathbb{R}}^n$，$f\in C(K,{\mathbb{R}}^m)$，$\epsilon >0$，存在 $k\in \mathbb{N}$，$A\in {\mathbb{R}}^{k\times n}$，$b\in {\mathbb{R}}^k$，$C\in {\mathbb{R}}^{m\times k}$，使得：

$$\underset{x\in K}{\sup }\Vert f(x)-g(x)\Vert <\epsilon$$

其中：

$$g(x)=C\cdot (\sigma \circ (A\cdot x+b))$$

这样的 $f$ 也可以用更大深度的网络来近似，方法是对第一层使用相同的结构，然后用后面的层近似恒等函数（identity function）。

证明：

足以证明，当 $m=1$，因为 ${\mathbb{R}}^m$ 上的一致收敛（uniform convergence），只是每个坐标中的一致收敛。

令 $F_{\sigma }$ 是所有单隐藏层神经网络的集合，神经网络使用 $\sigma$ 构造。令 $C_0({\mathbb{R}}^d,\mathbb{R})$ 是所有 $C({\mathbb{R}}^d,\mathbb{R})$ 的集合，具有紧支撑（compact support）。

如果函数是 $d$ 次多项式，那么 $F_{\sigma }$ 包含在所有 $d$ 次多项式的闭子空间中，所以它的闭包（closure）也包含在里面，这不是 $C_0({\mathbb{R}}^d,\mathbb{R})$ 的全部。

否则，我们表明 $F_{\sigma }$ 的闭包是全部的 $C_0({\mathbb{R}}^d,\mathbb{R})$。假设我们可以构建斜坡函数（ramp function）

r ( x ) = { − 1     if  x < − 1 x        if  ∣ x ∣ ≤ 1 1         if  x > 1 r(x)={

$$\begin{cases}-1\ \ \ {\text{ if }}x<-1\\x\ \ \ \ \ \ {\text{ if }}|x|\leq 1\\1\ \ \ \ \ \ \ {\text{ if }}x>1\\\end{cases}$$ } r(x)=⎩ ⎨ ⎧​−1    if x<−1x       if ∣x∣≤11        if x>1​

的任意好的近似值，则可以将其组合，以构造任意精度的任意紧支撑（arbitrary compactly-supported）的连续函数。它仍然是去近似斜坡函数。

任何机器学习中常用的激活函数显然都可以用来逼近斜坡函数，或者先逼近 ReLU，再逼近斜坡函数。

如果 $\sigma$ 是“压扁的（squashing）”，也就是说，它有极限 $\sigma (-\infty )<\sigma (+\infty )$，然后我们可以先仿射缩小它的 $x$ 轴，这样它的图形看起来像一个带有两个尖锐“过冲（overshoots）”的阶跃函数，然后对它们进行线性求和，使之成为斜坡函数的“阶梯（staircase）”近似。随着阶梯的步数增加，过冲趋于平缓，我们得到了斜坡函数的任意好的近似。

$\sigma$ 是一个通用的非多项式函数的情况下，难度更大。

通过允许将隐藏层的输出相乘（“pi-sigma networks”），可以消除多项式的问题，可以概括为：

pi-sigma networks 的通用逼近定理：

对于任何非恒值激活函数，单隐藏层 pi-sigma networks 是一个通用近似器。

3.3 任意深度的情况（Arbitrary-depth case）

该定理的“对偶（dual）”版本考虑了有界宽度和任意深度的网络。2017 年，Zhou Lu 等人针对任意深度情况证明了通用逼近定理的一个变体。他们表明，如果允许网络深度增长，具有 ReLU 激活函数的宽度为 $n+4$ 的网络可以近似于 $n$ 维输入空间上关于 $L^1$ distance 的任何勒贝格可积函数（Lebesgue integrable function）。还表明，如果宽度小于或等于 $n$，则这种近似任何勒贝格可积函数的一般表达能力就会丢失。在同一篇论文中，它表明宽度为 $n+1$ 的 ReLU 网络足以逼近任何 $n$ 维输入变量的连续函数。下面的细化指定了最佳最小宽度，这种近似是可能的并且是由于：

通用近似定理（L1 distance，ReLU activation，arbitrary depth，minimal width）：

对于任何 Bochner–Lebesgue p-integrable function $f:{\mathbb{R}}^n\to {\mathbb{R}}^m$ 和任何 $ϵ>0$，存在全连接的 ReLU 网络 $F$ 的宽度 d m = max ⁡ { n + 1 , m } d_{m}=\max\{{n+1},m\} dm​=max{n+1,m}，满足：

$${\int }_{{\mathbb{R}}^n}{\Vert f(x)-F_{}(x)\Vert }^p\mathrm{d}x<ϵ$$

此外，还有一个函数 $f\in L^p({\mathbb{R}}^n,{\mathbb{R}}^m)$ 和一些 $ϵ>0$，没有宽度小于 d m = max ⁡ { n + 1 , m } d_{m}=\max\{{n+1},m\} dm​=max{n+1,m} 的全连接 ReLU 网络满足上述近似界限。

定量细化（Quantitative Refinement）：当 $\mathcal{X}=[0,1{]}^d$，$D=1$，$\sigma$ 是 ReLU activation function，那么 ReLU 网络要达到的确切深度和宽度 $\epsilon$ 误差也是已知的。此外，如果目标函数 $f$ 是平滑的，那么所需的层数和它们的宽度可以呈指数级变小。即使 $f$ 不光滑，如果 $f$ 允许额外的“组合结构（compositional structure）”，就可以打破维数诅咒。

总之，现有相关论文（Kidger, Patrick, 2020）的中心结果为具有有界宽度的网络，提供了以下通用近似定理：

通用近似定理（Uniform non-affine activation, arbitrary depth, constrained width）：

令 $\mathcal{X}$ 是 ${\mathbb{R}}^d$ 的一个紧致子集（compact subset）。令 $\sigma :\mathbb{R}\to \mathbb{R}$ 是任何非仿射连续函数（non-affine continuous function），它至少在一点连续可微，在该点具有非零导数。令 ${\mathcal{N}}_{d,D:d+D+2}^{\sigma }$ 表示前馈神经网络的空间，神经网络具有 $d$ 个输入神经元，$D$ 个输出神经元，以及任意数量的隐藏层，每个隐藏层具有 $d+D+2$ 个神经元，这样每个隐藏的神经元都有激活函数 $\sigma$，并且每个输出神经元都与它的激活函数相同，其中输入层为 $\varphi$ 和输出层 $\rho$。然后考虑 $\epsilon >0$ 和任何 $f\in C(\mathcal{X},{\mathbb{R}}^D)$，存在 $\hat{f}\in {\mathcal{N}}_{d,D:d+D+2}^{\sigma }$，使得：

$$\underset{x\in \mathcal{X}}{\sup }\Vert \hat{f}(x)-f(x)\Vert <\epsilon$$

换句话说，就一致收敛的拓扑而言，$\mathcal{N}$ 在 $C(\mathcal{X};{\mathbb{R}}^D)$ 中是稠密的（dense）。

定量细化（Quantitative Refinement）：将 $f$ 近似为已知的 $\epsilon$ 精度所需的层数和每层的宽度；此外，当 $\mathcal{X}$ 和 ${\mathbb{R}}^D$ 被任何非正曲面黎曼流形取代时，结果是正确的。

有界宽度、任意深度情况的某些必要条件已经成立，但与已知的充分必要条件之间仍然存在差距。

3.4 有界深度和有界宽度的情况（Bounded depth and bounded width case）

Maiorov 和 Pinkus 获得了关于层数有限的神经网络近似能力的第一个结果，每层包含有限数量的人工神经元。他们非凡的结果表明，此类网络可以是通用近似器，并且为了实现此属性，两个隐藏层就足够了。

通用近似定理：

存在一个激活函数 $\sigma$ 是解析的、严格递增的，sigmoidal 函数的，具有以下性质：
对于任何 $f\in C[0,1{]}^d$，$\epsilon >0$，存在常量 $d_i,c_{ij},{\theta }_{ij},{\gamma }_i$，和矢量 ${\mathbf{w}}^{ij}\in {\mathbb{R}}^d$，对于全部 $\mathbf{x}=(x_1,...,x_d)\in [0,1{]}^d$：

$$\left|f(\mathbf{x})-\sum _{i=1}^{6d+3}{d}_i\sigma \left(\sum _{j=1}^{3d}{c}_{ij}\sigma ({\mathbf{w}}^{ij}\cdot \mathbf{x}-{\theta }_{ij})-{\gamma }_i\right)\right|<\epsilon$$

这是一个存在的结果。它说明，存在为有界深度有界宽度网络提供通用近似属性的激活函数。使用特定的算法和计算机编程技术，Guliyev 和 Ismailov 根据数值参数有效地构造了这样的激活函数。开发的算法允许人们立即计算实轴上任何一点的激活函数。理论结果可以表述如下：

通用近似定理：

令 $[a,b]$ 是实线的有限分段，$s=b-a$ 和
$\lambda$ 是任何正数。然后可以通过算法构造一个可计算的 sigmoidal 激活函数 $\sigma :\mathbb{R}\to \mathbb{R}$，它是无限可微的，在 $(-\infty ,s)$ 上严格增加，$\lambda$ 在 $[s,+\infty )$ 严格递增，并满足以下性质：

1. 对于任何 $f\in C[a,b]$，$\epsilon >0$ 存在数字 $c_1,c_2,{\theta }_1$ 和 ${\theta }_2$，对所有 $x\in [a,b]$ 使得：

$$|f(x)-c_1\sigma (x-{\theta }_1)-c_2\sigma (x-{\theta }_2)|<\epsilon$$

2. 对于在 $d$ 维箱 $[a,b{]}^d$ 中的任何连续函数 $F$，$\epsilon >0$，存在常数 $e_p$，$c_{pq}$，${\theta }_{pq}$ 和 ${\zeta }_p$ 使得不等式：

$$\left|F(\mathbf{x})-\sum _{p=1}^{2d+2}{e}_p\sigma \left(\sum _{q=1}^d{c}_{pq}\sigma ({\mathbf{w}}^q\cdot \mathbf{x}-{\theta }_{pq})-{\zeta }_p\right)\right|<\epsilon$$

对所有 $\mathbf{x}=(x_1,\dots ,x_d)\in [a,b{]}^d$ 都适用。 这里的权重 ${\mathbf{w}}^q$，$q=1,\dots ,d$，被固定如下：

$${\mathbf{w}}^1=(1,0,\dots ,0),{\mathbf{w}}^2=(0,1,\dots ,0),ldots,{\mathbf{w}}^d=(0,0,\dots ,1)$$

此外，所有系数 $e_p$，除了一个，是相等的。

这里

$\sigma :\mathbb{R}\to \mathbb{R}$ 在一些集合 $X$ 上严格增加

表示存在严格递增函数 $u:X\to \mathbb{R}$，使得 $|\sigma (x)-u(x)|\le \lambda$，对于所有 $x\in X$。显然，一个 $\lambda$ 递增函数表现得像一个通常的递增函数，像 $\lambda$ 变小了一样。在“深度-宽度（depth-width）”术语中，上述定理表示对于某些激活函数，depth-2 width-2 networks 是单变量函数的通用近似器，depth-3 width-(2d+2) networks 是 $d$ 元（$d>1$）变量函数通用近似器。

3.5 图形输入（Graph input）

在图上（或者更确切地说在图同构类（graph isomorphism classes）上）实现有用的通用函数近似一直是一个长期存在的问题。流行的图卷积神经网络（GCN 或 GNN）可以像 Weisfeiler–Leman graph isomorphism test 一样具有判别力。2020 年，Brüel-Gabrielsson 建立了一个通用近似定理结果，表明具有一定单射性质的图表示（graph representation）足以进行有界图上的通用函数近似和无界图上的受限通用函数近似，并附有 KaTeX parse error: Expected 'EOF', got '#' at position 3: O(#̲\text{edges}\ti…- runtimes method，这是一种在一组基准测试中以最先进的技术执行的方法。

4. 近似理论（Approximation theory）

wiki: Approximation theory

5. 米田引理（Yoneda lemma）

wiki: Yoneda lemma

---

• 参考文献

wiki: Universal approximation theorem

wiki: Hilbert’s thirteenth problem

维基百科: 希尔伯特第十三问题

维基百科: 志村五郎

wiki: Goro Shimura

VI Arnold, G Shimura. Superposition of algebraic functions, mathematical developments arising from Hilbert’s problems. AMS Proceedings of Symposia in Pure and Applied. 1976.

wiki: Kolmogorov–Arnold representation theorem

没解决这个 7 次方程问题，为何这三个数学家却很开心

Stephen Ornes. Mathematicians Resurrect Hilbert’s 13th Problem. Quanta Magazine. January 14, 2021

维基百科: 通用近似定理

在理解通用近似定理之前，你可能都不会理解神经网络

Andre Ye. You Don’t Understand Neural Networks Until You Understand the Universal Approximation Theorem. Analytics Vidhya. Jul 1, 2020.