动手学深度学习21 卷积层里的多输入多输出通道

1. 多输入多输出通道

通道数：会仔细设计的参数。

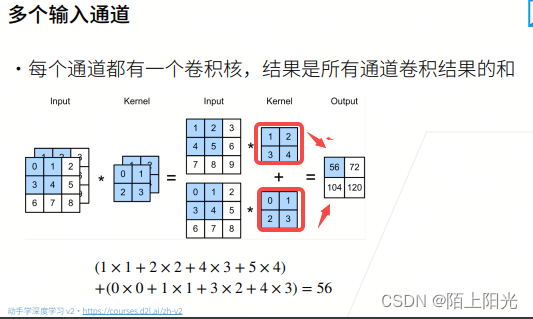
按位相加，输出结果。

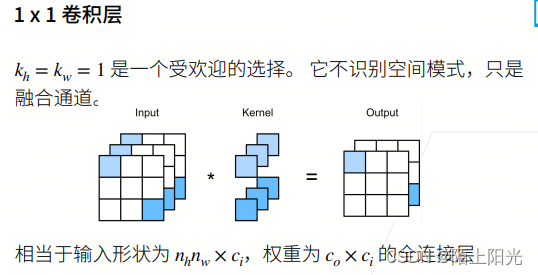
多输入通道–单个输出通道

输入输出通道没有太多相关性。

多输出通道，每个通道输出不同的模式【纹理】，这个输出通道丢给下一层做多输入通道，每个纹理做按权重相加，组合的模式识别。上层组合局部纹理，所有纹理组合起来–所有层加起来，最后能识别出一个猫。所以为什么要有多输入多输出通道。

1Gflop 10亿个浮点数运算

2. 代码实现

import torch
from d2l import torch as d2l

# def corr2d(X, K):
#   """计算二维互相关运算"""
#   h, w = K.shape
#   # 创建输出Y的shape，用0填充。
#   Y = torch.zeros((X.shape[0]-h+1, X.shape[1]-w+1))
#   for i in range(Y.shape[0]):
#     for j in range(Y.shape[1]):
#       Y[i, j] = (X[i:i+h, j:j+w] * K).sum()
#   return Y

# X = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
# K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
# print(X, K)

def corr2d_multi_in(X, K):
  # 先遍历“X”和“K”的第0个维度（通道维度），再把它们加在一起
  return sum(d2l.corr2d(x, k) for x, k in zip(X, K))

X = torch.tensor([[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],
           [[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]])
K = torch.tensor([[[0.0, 1.0], [2.0, 3.0]], [[1.0, 2.0], [3.0, 4.0]]])
print(X.shape, K.shape)
print(corr2d_multi_in(X, K), corr2d_multi_in(X, K).shape)

def corr2d_multi_in_out(X, K):
  # 迭代“K”的第0个维度，每次都对输入“X”执行互相关运算。
  # 最后将所有结果都叠加在一起
  return torch.stack([corr2d_multi_in(X, k) for k in K], 0)
K = torch.stack((K, K + 1, K + 2), 0)
print(K)
print(K.shape) # 3*2*2*2

print(corr2d_multi_in_out(X, K), corr2d_multi_in_out(X, K).shape)

# 1*1卷积
def corr2d_multi_in_out_1x1(X, K):
  c_i, h, w = X.shape
  c_o = K.shape[0]
  X = X.reshape((c_i, h*w))
  K = K.reshape((c_o, c_i))
  # 全连接层中的矩阵乘法
  Y = torch.matmul(K, X)
  return Y.reshape((c_o, h, w))

X = torch.normal(0, 1, (3, 3, 3))
K = torch.normal(0, 1, (2, 3, 1, 1))
Y1 = corr2d_multi_in_out_1x1(X, K)
Y2 = corr2d_multi_in_out(X, K)
# 很难保证全0，1e-6 有一点浮点精度的区别
assert float(torch.abs(Y1 - Y2).sum()) < 1e-6
print(Y1, Y1.shape)
print(Y2, Y2.shape)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

torch.Size([2, 3, 3]) torch.Size([2, 2, 2])
tensor([[ 56.,  72.],
        [104., 120.]]) torch.Size([2, 2])
tensor([[[[0., 1.],
          [2., 3.]],

         [[1., 2.],
          [3., 4.]]],


        [[[1., 2.],
          [3., 4.]],

         [[2., 3.],
          [4., 5.]]],


        [[[2., 3.],
          [4., 5.]],

         [[3., 4.],
          [5., 6.]]]])
torch.Size([3, 2, 2, 2])
tensor([[[ 56.,  72.],
         [104., 120.]],

        [[ 76., 100.],
         [148., 172.]],

        [[ 96., 128.],
         [192., 224.]]]) torch.Size([3, 2, 2])
tensor([[[-1.5234,  0.2240, -0.9463],
         [ 0.0801, -1.6338, -0.8454],
         [-2.7174,  2.3402, -3.1166]],

        [[-0.4025,  0.0149, -0.2325],
         [ 0.0160, -0.4428, -0.1675],
         [-0.6564,  0.5343, -0.7648]]]) torch.Size([2, 3, 3])
tensor([[[-1.5234,  0.2240, -0.9463],
         [ 0.0801, -1.6338, -0.8454],
         [-2.7174,  2.3402, -3.1166]],

        [[-0.4025,  0.0149, -0.2325],
         [ 0.0160, -0.4428, -0.1675],
         [-0.6564,  0.5343, -0.7648]]]) torch.Size([2, 3, 3])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

torch.stack()

torch.stack()是PyTorch中的一个函数，用于沿新的维度连接一系列张量。这个操作与torch.cat()类似，但torch.cat()是在已有维度上进行连接，而torch.stack()是在新的维度上进行堆叠。

使用示例

假设你有几个形状相同的张量，并希望将它们堆叠成一个新的张量，可以使用torch.stack()。

示例代码

import torch

# 创建三个形状相同的一维张量
tensor1 = torch.tensor([1, 2, 3])
tensor2 = torch.tensor([4, 5, 6])
tensor3 = torch.tensor([7, 8, 9])

# 使用 torch.stack 将它们沿新的维度堆叠
stacked_tensor = torch.stack([tensor1, tensor2, tensor3])

print(stacked_tensor)
1
2
3
4
5
6
7
8
9
10
11

输出

tensor([[1, 2, 3],
        [4, 5, 6],
        [7, 8, 9]])
1
2
3

在这个例子中，torch.stack([tensor1, tensor2, tensor3])操作创建了一个新的维度，将这三个一维张量堆叠成一个二维张量。新的维度的大小为3，对应于传入的张量的数量。

参数解释

• tensors (sequence of Tensors): 需要堆叠的张量序列。所有张量必须具有相同的形状。
• dim (int): 要插入的维度的位置。新的维度将插入到这个位置，默认值为0。

指定维度参数

你可以通过指定dim参数来控制新的维度的位置。

# 创建三个形状相同的二维张量
tensor1 = torch.tensor([[1, 2, 3], [4, 5, 6]])
tensor2 = torch.tensor([[7, 8, 9], [10, 11, 12]])
tensor3 = torch.tensor([[13, 14, 15], [16, 17, 18]])

# 沿第0维度堆叠
stacked_tensor_dim0 = torch.stack([tensor1, tensor2, tensor3], dim=0)
print(stacked_tensor_dim0.shape)  # torch.Size([3, 2, 3])

# 沿第1维度堆叠
stacked_tensor_dim1 = torch.stack([tensor1, tensor2, tensor3], dim=1)
print(stacked_tensor_dim1.shape)  # torch.Size([2, 3, 3])

# 沿第2维度堆叠
stacked_tensor_dim2 = torch.stack([tensor1, tensor2, tensor3], dim=2)
print(stacked_tensor_dim2.shape)  # torch.Size([2, 3, 3])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

在这个例子中，原始张量是形状为[2, 3]的二维张量。通过指定不同的dim参数，可以控制新的维度的位置，从而影响堆叠后的张量的形状。

总结

torch.stack()是一个强大的工具，用于沿新维度连接一系列形状相同的张量。这对于需要批量处理或组织数据的任务非常有用。通过调整dim参数，你可以灵活地控制新维度的插入位置，从而改变结果张量的形状。

3. QA:

20：输入通道是给定的，输出是可以任意设定的，但是不能随意设定，通常当不该变输入输出的高宽的情况下，通道数一般是不变的；当输入输出高宽减半的情况下，通道数一般是要加一倍，把空间信息压缩了，把提取到的信息在更多的通道上存储下来。
21：padding0不会影响精度，计算出来是一个常数，会影响计算性能
22：一般不同通道的卷积核是一样的，计算上效率更高。可以让卷积核不一样。
23：bias，当数据均值不为0的时候，偏移等于均值的复数。会做大量均值化的操作，bias影响很小。
24：核的参数是学习出来的，不是自己设置的。
25：二维卷积，输入图只有高宽。通道数是额外的东西。多了深度维度，是三维卷积，输入图=输入通道*深度*宽*高, 卷积核是5D的张量，输出通道也是4D的。
26：二维卷积，卷积核是二维的矩阵 。 ??
27: 假设高频低频数据都有，会有通道学习高频有些学习低频，数据丢给卷积网络学习。
28:1*1 计算单元周边的元素不参与卷积运算，即不识别空间模式。
29：MobileNet 不做通道的融合，先对每个输入通道做3*3的卷积，做完之后在每一个做空间融合， 计算复杂度很低。
https://baijiahao.baidu.com/s?id=1781528877664258115&wfr=spider&for=pc
30： 卷积能获取位置信息，对位置非常敏感。位置信息在输出元素的序列里面。
31：通道之间不共享参数。每个通道识别不同的模式。
32：计算复杂度，每一个输出的元素需要多少东西计算出来。
33：计算量跟nh nw相关。
34：希望卷积核识别纹理，卷积核自己识别出来的。每个卷积层学到一点点东西，层层精炼。
35：训练数据存到磁盘上再读回来。开发工具看个人喜好。
36：输入通道是3通道，代码输入必须设成3通道，输出可以设成10.
37：feature map 卷积的输出
38：输入通道不能变，固定。
39：卷积核可以试奇数。
40：3d卷积处理视频。3d比2d效果好一点点，但计算复杂度高很多。