- 1redis的哨兵模式集群搭建和去中心化集群搭建_去中心化节点如何构建集群
- 2从加密到签名:如何使用Java实现高效、安全的RSA加解密算法?
- 3stream流详解(JDK1.8的特性)_stram流详解
- 4Kafka(分布式发布订阅消息系统) 简介_什么是kafka
- 5全量微调Llama2-7b遇到的错误(stanford_alpaca)_bash pretrain_llama2_7b_distributed_zl200
- 6spark页面8080端口访问打不开_spark 启动正常 但是访问不了
- 7Selenium的百度高级搜索-自动化(未完成)
- 8numpy的使用_numpy 使用
- 9程序员思维训练500题(附带答案)_编程思维训练500题
- 104—python函数知识小结_python四级知识汇总
灰狼优化算法(GWO)
赞
踩
一、背景知识
灰狼优化算法(Grey Wolf Optimizer, GWO),由澳大利亚格里菲斯大学学者Mirjalili等人于2014年提出来的一种群智能优化算法。灵感来自于灰狼群体捕食行为。GWO算法模拟了自然界中灰狼的领导等级和狩猎机制。将灰狼分为四种类型,用来模拟等级阶层。此外,还模拟了寻找猎物、包围猎物和攻击猎物三个主要阶段。
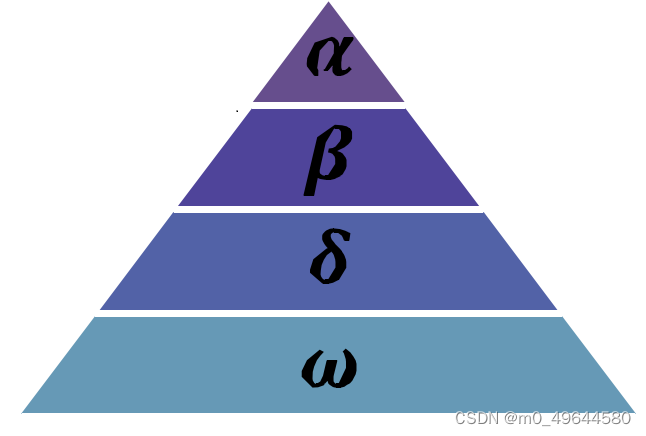
图1 灰狼等级分层
灰狼群一般分为4个等级:处于第一等级的灰狼是领头狼,用α表示,它们主要负责各类决策,然后将决策下达至整个种群;处于第二阶级的灰狼用β表示,称为从属狼,用于辅助α狼制定决策或其他种群活动;处于第三阶段的灰狼用δ表示,侦察狼、守卫狼、老狼和捕食狼都是这一类。处于第四等级的灰狼用ω表示,它们在灰狼群中扮演了"替罪羊"的角色(好惨),同时它们必须要屈服于其他等级的狼。
二、算法原理
GWO 优化过程包含了灰狼的社会等级分层、跟踪、包围和攻击猎物等步骤:
(1)社会等级分层
依据上述灰狼等级制度,可以对灰狼的社会等级进行数学建模,认为最合适的解是α,那么第二和第三最优解分别表示为β和δ,而剩余其他解都假定为ω。在GWO中,通过α、β和δ来导引捕食(优化),ω听从于这三种狼。
(2)包围猎物
灰狼在搜索猎物时会逐渐地接近猎物并包围它,其包围猎物的数学模型为:
(1)
(2)
其中,X 表示灰狼的位置;t 为当前迭代次数;Xp表示猎物的位置;D表示灰狼与猎物之间的距离,其计算方式见公式(2)。 A 和 C 是两个协同系数向量, 其计算见公式(3)和公式(4)。
(3)
(4)
式(3)中,向量A用于模拟灰狼对猎物的攻击行为,它的取值收到a的影响。a是收敛因子,其是一个平衡GWO勘探与开发能力的关键参数,在整个迭代过程中,a由2降到0。
(3)狩猎行为
灰狼能够识别猎物的位置并包围它们。灰狼具有识别潜在猎物(最优解)位置的能力,当灰狼识别出猎物的位置后,β 和 δ 在 α 的带领下指导狼群包围猎物。在优化问题的决策空间中,我们对最佳解决方案(猎物的位置)并不了解。因此,为了模拟灰狼的狩猎行为,我们假设 α ,β 和 δ 具有较强识别潜在猎物位置的能力。因此,在每次迭代过程中,保留当前种群中的最好三只灰狼( α、β、δ),然后根据它们的位置信息来更新其它搜索代理(包括 ω)的位置。
灰狼个体跟踪猎物位置的数学模型描述如下:
(5)
其中,,
,
分别表示α ,β ,δ 与其他个体间的距离。
,
,
分别代表α ,β ,δ的当前位置,
,
,
是随机向量,
是当前灰狼的位置。当|A|>1时,灰狼之间尽量分散在各区域并搜寻猎物。当|A|<1时,灰狼将集中捜索某个或某些区域的猎物。
(6)
(7)
式(6)分别定义了狼群中 ω 个体朝向 α ,β 和 δ 前进的步长和方向,式(7)定义了 ω 的最终位置。
(4)攻击猎物
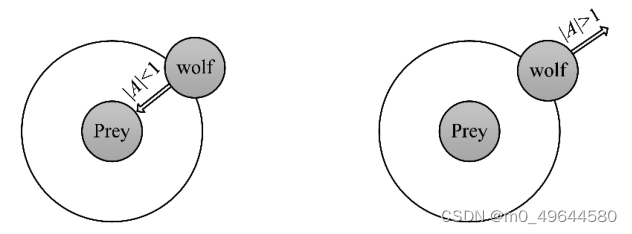
当猎物停止移动时,灰狼通过攻击来完成狩猎过程。为了模拟逼猎物,a的值被逐渐减小,因此 A ⃗的波动范围也随之减小。换句话说,在迭代过程中,当 a 的值从2线性下降到0时,其对应的 A 的值也在区间[-a,a]内变化。如图a所示,当 A的值位于区间内时,灰狼的下一位置可以位于其当前位置和猎物位置之间的任意位置。当∣A ∣ < 1 时,狼群向猎物发起攻击(陷入局部最优)。
(a) (b)
(5)寻找猎物
灰狼根据 α ,β 和 δ 的位置来搜索猎物。灰狼在寻找猎物时彼此分开,然后聚集在一起攻击猎物。对于分散模型的建立,通过|A|>1使其捜索代理远离猎物,这种搜索方式使 GWO 能进行全局搜索,强调了勘探(探索)并允许 GWO 算法全局搜索最优解。如图b所示,∣A ∣ > 1 强迫灰狼与猎物(局部最优)分离,希望找到更合适的猎物(全局最优)。GWO 算法中的另一个搜索系数是C。从2.2中的公式可知,C向量是在区间范围[0,2]上的随机值构成的向量,此系数为猎物提供了随机权重,以便増加(|C|>1)或减少(|C|<1)。这有助于 GWO 在优化过程中展示出随机搜索行为,以避免算法陷入局部最优。值得注意的是,C并不是线性下降的,C在迭代过程中是随机值,该系数有利于算法跳出局部,特别是算法在迭代的后期显得尤为重要。这样,从最初的迭代到最终的迭代中,它都提供了决策空间中的全局搜索。在算法陷入了局部最优并且不易跳出时,C的随机性在避免局部最优方面发挥了非常重要的作用,尤其是在最后需要获得全局最优解的迭代中。
三、算法流程
Step1.初始化种群参数:包括种群数量N,最大迭代次数Maxlter,调控参数a,A。
Step2.根据变量的上下界来随机初始化灰狼个体的位置X。
Step3.计算每一头狼的适应度值,并将种群中适应度值最优的狼的位置信息保存,将种群中适应度值次优的狼的位置信息保存为
,将种群中适应度第三优的灰狼的位置信息保存为
。
Step4.更新灰狼个体X的位置。
Step5.更新参数a,A和C。
Step5.计算每一头灰狼的适应度值,并更新三匹头狼的最优位置。
Step5.判断是否到达最大迭代次数Maxlter,若满足则算法停止并返回Xa的值作为最终得到的最优解,否则转到Step4。