浅析扩散模型与图像生成【应用篇】(九)——Pix2pix-zero_扩散模型生成图片实例

9. Zero-shot Image-to-Image Translation

  该文提出一种无需训练，即可对图像进行文本驱动编辑的方法。在准确修改目标对象的同时，保证原图的背景和布局等内容不受太多的影响。下图展示了几种文本驱动图像编辑的效果，如将猫变成狗，将马变成斑马等。

  该文主要做了以下几点工作，首先将输入的图像$\tilde{x}$利用Stable Diffusion编码到潜在空间得到$x_0$，并按照DDIM中的确定性过程将其扩散为噪声编码$x_{inv}$。然后，利用BLIP模型得到输入图像对应的文本描述$c$，并计算其与目标文本提示$t$之间的均值差异$\Delta c_{edit}$，将其作为图像编辑的方向引入到生成过程中。最后，为了保持图像的背景和布局保持不变，作者引入了交叉注意力机制进行引导。该方法的流程如下图所示

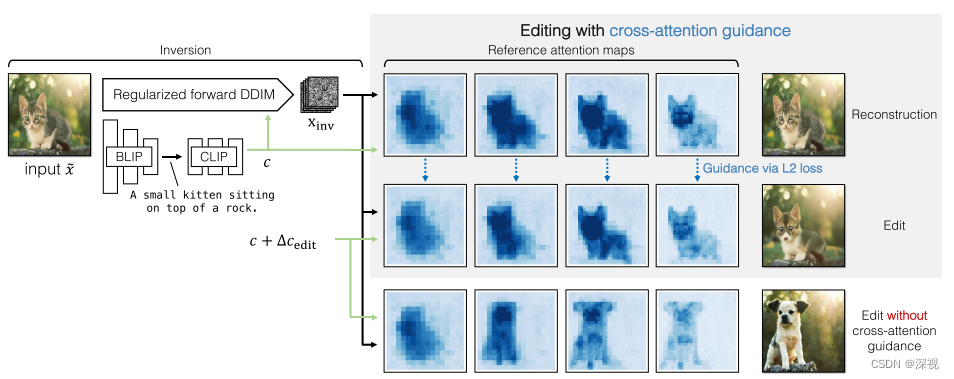
1. 逆转真实图像

  首先得到真实图像$\tilde{x}$对应的潜在特征$x_0$后，作者利用DDIM中的确定性过程将其扩散为纯噪声，过程如下$$x_{t+1}=\sqrt{{\bar{\alpha }}_{t+1}}{f}_{\theta }\left(x_t,t,c\right)+\sqrt{1-{\bar{\alpha }}_{t+1}}{ϵ}_{\theta }\left(x_t,t,c\right)$$其中，${ϵ}_{\theta }$是基于UNet模型的噪声估计器，$f_{\theta }$是根据当前的噪声图像$x_t$，时刻$t$和文本描述特征$c$来估计得到的${\hat{x}}_0$过程如下$$f_{\theta }\left(x_t,t,c\right)=\frac{x_t-\sqrt{1-{\bar{\alpha }}_t}{ϵ}_{\theta }\left(x_t,t,c\right)}{\sqrt{{\bar{\alpha }}_t}}$$

这里很有意思，作者并不是直接使用DDIM中的扩散过程来增加噪声的，而是将原本已知的$x_0$换成了估计得到的${\hat{x}}_0$，把可以随机采样的噪声$ϵ$变成了预测得到的${ϵ}_{\theta }$，我认为这样做的目的是为了在扩散过程中就把文字描述特征$c$引入进去。

  但是估计得到的噪声${ϵ}_{\theta }$存在一个问题，他不一定满足统计学上的不相关性，也就是说它不是一个完全的高斯白噪声，这将导致由最终的扩散结果$x_{inv}$生成的图像效果不好。为了解决这个问题，作者引入了两个正则化条件，${\mathcal{L}}_{pair}$和${\mathcal{L}}_{KL}$。为了计算${\mathcal{L}}_{pair}$，作者将${ϵ}_{\theta }$输出的噪声图${\eta }^0\in {\mathbb{R}}^{64\times 64\times 4}$利用2*2的全局池化层将其逐步下采样到尺寸为$8\times 8$的噪声图，构建一个4层的噪声图金字塔 { η 0 , η 1 , η 2 , η 3 } \{\eta^0,\eta^1,\eta^2,\eta^3\} {η0,η1,η2,η3}，然后，利用下式来计算${\mathcal{L}}_{pair}$$${\mathcal{L}}_{\text{pair }}=\sum _p\frac{1}{S_p^2}\sum _{\delta =1}^{S_p-1}\sum _{x,y,c}{\eta }_{x,y,c}^p\left({\eta }_{x-\delta ,y,c}^p+{\eta }_{x,y-\delta ,c}^p\right)$$其中，下标$x,y$表示位置，$c$表示通道号，$\delta$表示位置偏移量，$S_p$表示噪声图的尺寸。另一方面，使用变分自动编码器中的KL散度损失${\mathcal{L}}_{KL}$，来约束生成的噪声满足零均值单位方差的要求。最后，两个损失函数通过加权求和作为最终的自动互相关（auto-correlation）正则化项${\mathcal{L}}_{auto}={\mathcal{L}}_{pair}+\lambda {\mathcal{L}}_{KL}$。

2. 计算编辑方向

  作者把原本的文本描述$c$作为源提示$s$，把编辑后的文本描述作为目标提示$t$，并利用GPT-3语言模型，根据这两个提示分别生成一系列的句子，然后利用CLIP的文本编码器得到这些句子的嵌入式特征，并计算二者之间的均值差异$\Delta c_{edit}$，如下图所示。这个差异将作为图像编辑的方向引入到生成过程中。

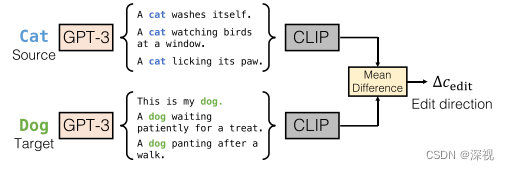
3. 基于交叉注意力引导的图像编辑

  此时我们已经得到了扩散后的噪声图像$x_{inv}$和原本的图像描述$c$,以及图像编辑的方向$\Delta c_{edit}$。最直接的方法就是将图像描述和编辑方向相加后$c_{edit}=c+\Delta c_{edit}$作为条件，引入噪声估计网络${ϵ}_{\theta }(x_t,t,c_{edit})$，并按照一般的反向去噪过程得到生成图像，如本文中第二幅图的最后一行表示的过程。但这样带来一个问题，就是虽然目标对象按照编辑的内容发生了改变，但由于缺少约束和引导，图像的背景布局以及目标的结构和姿态都发生了变化，这是我们不希望看到的。因此为了解决这个问题，作者引入了基于交叉注意力机制的引导方法。
  其实在Prompt-to-prompt这篇文章中，我们就已经揭示了交叉注意力图和图像内容以及文字描述之间的对应关系，如下所示 Attention ⁡ ( Q , K , V ) = M ⋅ V  where  M = Softmax ⁡ ( Q K T d )

$$\begin{aligned} \operatorname{Attention}(Q, K, V) & =M \cdot V \\ \text { where } M & =\operatorname{Softmax}\left(\frac{Q K^{T}}{\sqrt{d}}\right) \end{aligned}$$ Attention(Q,K,V) where M​=M⋅V=Softmax(d ​QKT​)​其中$Q=W_Q\psi (x_t),K=W_{K}c,V=W_{V}c$，$\psi (x_t)$表示经过UNet编码的图像特征。得到的交叉注意力图$M$其中的每个元素$M_{ij}$表示了第$j$个文本提示对于图像中第$i$个位置处的作用。因此为了保证图像的整体背景和布局不会随着文本编辑发生较大的改变，作者提出了一种基于交叉注意力机制的引导。
  第一步，直接使用原本的图像描述$c$获得交叉注意力图$M_t^{ref}$；第二步，使用编辑后的描述$c_{edit}$获得交叉注意力图$M_t^{edit}$，计算两者差异的L2范数关于$x_t$的梯度$\Delta x_t={\nabla }_{x_t}\left({\Vert M_t^{\text{edit }}-M_t^{\text{ref }}\Vert }_2\right)$，并将其作用于$x_t$，得到${\tilde{x}}_t=x_t-{\lambda }_{xa}\Delta x_t$后，再次计算噪声${ϵ}^{\widehat{edit}}\leftarrow {ϵ}_{\theta }\left(x_t-{\lambda }_{\text{xa }}\Delta x_t,t,c_{\text{edit }}\right)$。最后，根据${ϵ}^{\widehat{edit}}$进行反向去噪，得到$x_{t-1}$。完整的算法流程如下图所示