【动态规划】投资问题_投资问题动态规划算法

本文利用markdown基于https://blog.csdn.net/qq_41926985/article/details/105627049重写,代码部分为本人编辑

代码要求

应用动态规划方法，求解投资问题，实现下面的例子。

#define MAX_N 4 //最大投资项目数目
#define MAX_M 5 //最大投资钱数(万元)
//f[i][j]的意义：第 i（从 1 开始）个项目投资 j 万元的收益
int f[MAX_N+1][MAX_M+1] = {
    {0,0,0,0,0,0},
    {0,11,12,13,14,15},
    {0,0,5,10,15,20},
    {0,2,10,30,32,40},
    {0,20,21,22,23,24}
}; 
1
2
3
4
5
6
7
8
9
10

投资问题

什么是投资问题

有$m$元钱，$n$项投资，$f_i(x)$：将x元投入第i个项目的效益。求使得的总效益最大的投资方案。

举个例子：现在有两个项目x是钱数(单位：元)，

$f_i(x)$：将x元钱投资到第i个项目产生的效益

注意：使用的是总共的x钱数投资两个项目，而不是分别投资。

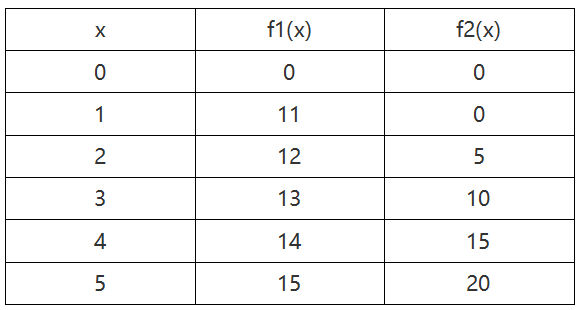
将0元投资这两个项目，则最大收益就是0

将1元投资这两个项目，不难看出

$$f_1(1)+f_2(0)=11$$

，是最大收益

将2元投资这两个项目，不难看出

$$f_1(2)+f_2(0)=12$$

，是最大收益

将3元投资这两个项目,

$$max(f_1(0)+f_2(3)，f_1(1)+f_2(2)，f_1(2)+f_2(1)，f_1(3)+f_2(0))=f_1(1)+f_2(2)=16$$

,是最大收益

同样的用4元或者5元投资这两个项目，所带来的最大收益分别是21和26

我们接下来对问题进行建模：

目标函数：利用所分配的投资产生最大效益

约束条件：是在总资金的条件下进行投资

建模：

问题的解是向量$<x_1,x_2,\cdot \cdot \cdot ,x_n>$

$x_i$是投给项目的钱数，$i=1,2,\cdot \cdot \cdot ,n.$

目标函数 m a x { f 1 ( x 1 ) + f 2 ( x 2 ) + ⋅ ⋅ ⋅ + f n ( x n ) } max \{f_1(x_1)+f_2(x_2)+···+f_n(x_n)\} max{f1​(x1​)+f2​(x2​)+⋅⋅⋅+fn​(xn​)}

约束条件：$x_1+x_2+\cdot \cdot \cdot +x_n=m,x_i\in N$

下面我们来考虑用动态规划算法来解投资问题

动态规划算法来解投资问题

子问题的界定：由参数$k$和$x$界定

$k$:考虑对每个项目$1，2，\dots ，k$的投资

$x$:投资总钱数不超过$x$的

接下来我们再看一下递推方程

设$F_k(x):x$元钱投给前k个项目的最大效益

我们可以这么想，假如我们要求$F_k(x)$,即就是求x元钱投给前$k$个项目的最大效益。那不妨求$p$元钱$(p\le x)$投给前k-1个项目的最大效益$F_{k-1}(p)$,进而确定$F_k(x)$

我们进而可以列出递推方程：

我们看到啊，$F_k(x)$的求解，就是去求用$x-x_k$分配前$k-1$个项目所产生的最大效益。然而这个最大效益是在备忘录存着来。没错备忘录的作用就是存储最大的效益。
$F_1(x)$：就是在投资表中的用x钱投资第一个项目的收益

接下来我们看个例子：
这是一个投资——效益表

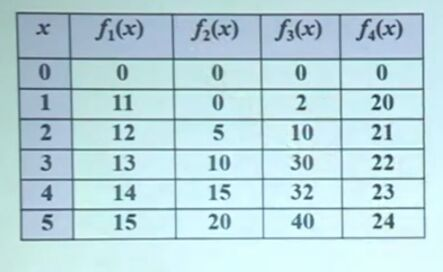
我们要先明确最小子问题是什么，然后才能从这个最小子问题开始算起；然后考虑计算顺序，保证后面的值在前面已经计算好。

这里我们看到第一个项目的最大收益就是投资对应的收益，即
$$F_1(0)=0，F_1(1)=11，F_1(2)=12，F_1(3)=13，F_1(4)=14，F_1(5)=15。\text{\hspace{1em}(1)}$$

我们能看到啊，前1个项目可以定为最小子问题，它的初值可以通过查表得到，不用计算。而后面的项目随着项目的增多，子问题的复杂性就会增强。因此我们根据项目序列的递增关系来计算，从而保证后面的值在前面已经计算好了。

我们通过上面的递推方程可以得知，用$x-x_k$分配前$k-1$个项目所产生的最大效益越大以及x元钱投给前k个项目的最大效益越大，从而使得原问题的解达到最大。进而满足依赖关系。而对于$x_k$为何值，这个是需要通过计算获取最优解来得到。

好，我们来继续看前两个项目的最大效益：
我们先看$x=0$，则最大效益是0

再来看$x_k=1$， F 2 ( 1 ) = m a x { f 2 ( 1 ) + F 1 ( 1 − 1 ) ， f 2 ( 0 ) + F 1 ( 1 − 0 ) } = 11 F_2(1)=max\{f_2(1)+F_1(1-1)，f_2(0)+F_1(1-0)\}=11 F2​(1)=max{f2​(1)+F1​(1−1)，f2​(0)+F1​(1−0)}=11
再来看$x_k=2$， F 2 ( 2 ) = m a x { f 2 ( 2 ) + F 1 ( 2 − 2 ) ， f 2 ( 1 ) + F 1 ( 2 − 1 ) ， f 2 ( 0 ) + F 1 ( 2 − 0 ) } = 12 F_2(2)=max\{f_2(2)+F_1(2-2)，f_2(1)+F_1(2-1)，f_2(0)+F_1(2-0)\}=12 F2​(2)=max{f2​(2)+F1​(2−2)，f2​(1)+F1​(2−1)，f2​(0)+F1​(2−0)}=12
再来看$x_k=3$， F 2 ( 3 ) = m a x { f 2 ( 3 ) + F 1 ( 3 − 3 ) ， f 2 ( 2 ) + F 1 ( 3 − 2 ) ， f 2 ( 1 ) + F 1 ( 3 − 1 ) ， f 2 ( 0 ) + F 1 ( 3 − 0 ) } = 16 F_2(3)=max\{f2(3)+F_1(3-3)，f_2(2)+F_1(3-2)，f_2(1)+F_1(3-1)，f_2(0)+F_1(3-0)\}=16 F2​(3)=max{f2(3)+F1​(3−3)，f2​(2)+F1​(3−2)，f2​(1)+F1​(3−1)，f2​(0)+F1​(3−0)}=16
同样的$F_2(4)=21，F_2(5)=26$

当然，这里得到的$F_2(1)，F_2(2)，F_2(3)，F_2(4)，F_2(5)$要记录到备忘录里面。

那么如何去记录解？
我们用$s$数组来记录解。我们去记录在得到最大效益的时候，最后一个项目给了多少钱。
就如同上面的例子，在前两个项目的最大收益中。
$x_i(x):$分配x元钱给前i个项目，在最大收益时，第i个项目得到了多少钱
$x_2(1):$看到啊，$F_2(1)=f_2(0)+F_1(1-0)=11$。此时，第2个项目得到了0元钱
$x_2(2):f_2(0)+F_1(2-0)=12$。此时，第2个项目得到了0元钱
$x_2(3):f_2(2)+F_1(3-2)=16$。此时，第2个项目得到了2元钱
同样的，我们也能得到$x_2(4)=3，x_2(5)=4$

ok，下面介绍一下如何追踪解
上面的投资问题的结果如图所示：

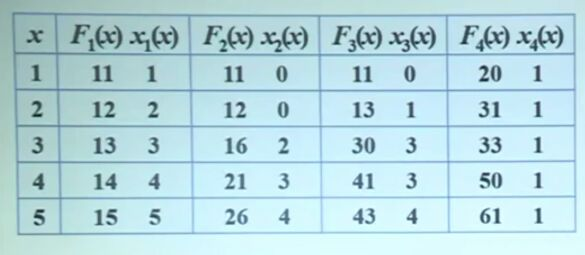
我们细想，原问题是用5元钱分配所有项目（这里就是4个项目）,所得到的最大收益
这个最大收益是不是就是$F_4(5)$
($F_4(5)$：用5元钱分配前4个项目得到的最大收益)
,那这个值就可以去衡量原问题的解。因此我们追踪解也要从$x_4(5)$开始，自底向上追踪。

先看到x4(5)=1，说明达到最大收益的时候分配给最后一个项目，即第4个项目是1元钱。
那么第3个项目呢？
第3个项目就是$x_3(x)$,这个x就是5-1=4，就是用总共的5元钱-分配给第4个项目的钱数。
$x_3(5-1)=3$。因此在得到最大收益时，分配给第3个项目3元钱。
同理$x_2(4-3)=0，x_1(1-0)=1$
也许你会问为什么要这么解？
我们看那个递推方程，我们既然知道$F_4(x_5)=f_4(x_4)+F_3(x-x_4)$。然而我们知道了在最大收益时，分配给第4个项目1元钱，这个可以通过代码可以实现。

则$F_3(4)$，这个通过查表即可得到41，此时分配给它的钱就是3。同样的也可以逆推出$F_2$和$F_1$中的$x_2和x_1$。就是通过前k-1个项目的最大收益+用剩下钱分配给第k个项目的收益。然而前$k-1$个项目的最大收益是保存在了我们的备忘录中，所以这个值不仅可以查到，而且它只计算了一次。没有重复计算。使得这个唯一确定的值+$f_4(x_4)$值就是最大收益。

因此我们抛去$f_4(x_4)$的值，也就是前k个项目的最大收益$F_3(x-x_4)$。

因此我们可以通过查表得到$x_3(x-x_4)$。故这样计算是合理的

#include<bits/stdc++.h>
using namespace std;
#define MAX_N 4 //最大投资项目数目
#define MAX_M 5 //最大投资钱数(万元)
//f[i][j]的意义：第 i（从 1 开始）个项目投资 j 万元的收益
int f[MAX_N+1][MAX_M+1] = {
    {0,0,0,0,0,0},
    {0,11,12,13,14,15},
    {0,0,5,10,15,20},
    {0,2,10,30,32,40},
    {0,20,21,22,23,24}
}; 

void printNum(int num[MAX_N+1][MAX_M+1]){
    for(int i=0;i<=MAX_M;i++)
    {
        for(int j=0;j<=MAX_N;j++)
        {
            cout << num[j][i] << " ";
        }
        cout << endl;
    }
    return;
}

int main()
{
    int s[MAX_N+1][MAX_M+1] = {0};//s数组用于记录最后一个项目分配的钱
    int F[MAX_N+1][MAX_M+1] = {0};
    for(int i=0;i<=MAX_M;i++){
        F[1][i] = f[1][i];
        s[1][i] = i;
    }

    
    for(int i=2;i<=MAX_N;i++)
    {
        for(int j=0;j<=MAX_M;j++)
        {
            int max = F[i-1][j];
            int cnt = 0;
            for(int k=0;k<=j;k++)
            {
                int num = f[i][k]+F[i-1][j-k];
                if(num>=max)
                {
                    max = num;
                    cnt = k;
                }
            }
            F[i][j] = max;
            s[i][j] = cnt;
        }
    }
    

    printNum(f);
    cout << endl;
    printNum(s);
    cout << endl;
    printNum(F);
    cout << endl;

    int res = s[MAX_N][MAX_M];
    int pro = MAX_N;
    int m = MAX_M;

    while(pro>0)
    {
        cout << "第" << pro << "个项目的钱数为：" << res << endl;;
        pro-=1;
        m-=res;
        res = s[pro][m];
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76