- 1HBase 开始运行
- 2python计算机毕设【附源码】4s店汽车销售管理系统(django+mysql+论文)_汽车销售系统python课程设计
- 3python打包分发工具:setuptools_python打包setuptools
- 42023年,自动化测试会取代手工测试吗?
- 5GhostNet V2家族大放异彩:华为GhostNet,超越谷歌MobileNet的CVPR2020计算机视觉技术
- 6calc(100vh - 10px) calc(100vw - 10px) calc(100% - 10px) 简单说明_calc 100vh
- 77月最新阿里菜鸟国际Java研发岗面经分享,2024年最新spring dubbo面试题_菜鸟java面试
- 8多源BFS
- 9我国人工智能核心产业规模近6000亿元
- 10人工智能第三版|chap01|task01
【数学建模】MATLAB入门教程:插值与拟合(下)
赞
踩
前言
插值与拟合在数据处理和科学计算中扮演着非常重要的角色,它们用于估算未知数据点的值,帮助我们理解和预测数据趋势
一、一维插值
1、一维插值定义
已知n+1个节点(,
)(j=0,1,...,n,其中
互不相同,不妨设a=
<
<...<
=b),求任一插值点
(!=
)处的插值
解决方法:构造一个相对简单的函数y=f(x),通过全部节点,即f()=
(j=0,1,...,n)
再用f(x)计算插值,即=f(
)
2、常见方法
1、拉格朗日插值:已知函数f(x)在n+1个节点,
,···,
处的函数值为
,
,···,
.求一n次多项式
(x),使其满足:
(
)=
,i=0,1,...,n.解决此问题的拉格朗日插值多项式公式如下:
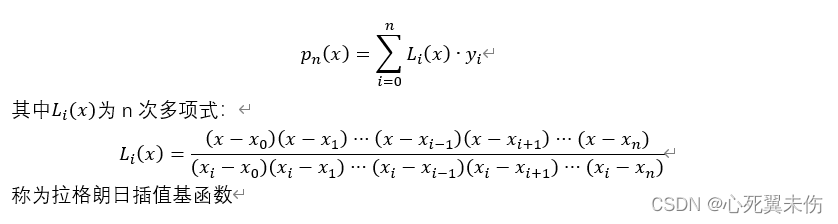
特别地:两点一次(线性)插值多项式
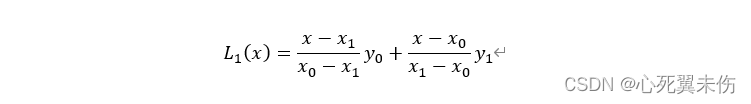
例题 g(x)=1/(1+x^2),-5<=x<5.采用拉格朗日多项式插值:选取不同插值节点n+1个,其中n为插值多项式的次数,当n分别区2,4,6,8,10时,绘出插值结果图形
- function lagrange_interpolation_example
- % 定义函数 g(x)
- g = @(x) 1 ./ (1 + x.^2);
-
- % 定义插值区间和次数
- x_interval = [-5, 5];
- n_values = [2, 4, 6, 8, 10];
-
- % 初始化图形
- figure;
- hold on;
-
- % 绘制原始函数
- x_fine = linspace(x_interval(1), x_interval(2), 1000);
- y_fine = g(x_fine);
- plot(x_fine, y_fine, 'b-', 'LineWidth', 2);
-
- % 对于每个n值,计算并绘制拉格朗日插值
- for n = n_values
- % 在区间上均匀选择n+1个插值节点
- x_nodes = linspace(x_interval(1), x_interval(2), n + 1);
- y_nodes = g(x_nodes);
-
- % 计算拉格朗日插值多项式并绘制结果
- [x_lagrange, y_lagrange] = lagrange_poly(x_fine, x_nodes, y_nodes);
- plot(x_lagrange, y_lagrange, 'DisplayName', sprintf('n=%d', n), 'LineWidth', 1.5);
- end
-
- % 添加图例、标签和标题
- legend('Original Function', sprintf('Lagrange Interpolation, n=%d', n_values));
- xlabel('x');
- ylabel('g(x)');
- title('Lagrange Interpolation of g(x) = 1 / (1 + x^2)');
- grid on;
- hold off;
- end
-
- function [x_lagrange, y_lagrange] = lagrange_poly(x, x_nodes, y_nodes)
- % 拉格朗日插值多项式计算函数
- n = length(x_nodes) - 1;
- y_lagrange = zeros(size(x));
-
- for i = 1:n+1
- % 计算拉格朗日基函数
- L_i = 1;
- for j = 1:n+1
- if j ~= i
- L_i = L_i * (x - x_nodes(j)) / (x_nodes(i) - x_nodes(j));
- end
- end
- % 累加基函数与对应函数值的乘积
- y_lagrange = y_lagrange + L_i * y_nodes(i);
- end
-
- % 返回插值点x和对应的插值结果y_lagrange
- x_lagrange = x;
- end
-
- % 调用函数以运行示例
- lagrange_interpolation_example

2、分段线性插值:将每两个相邻的点用直线连接起来,如此形成的一条折线就是分段线性插值函数(x),它满足
(
)=

计算量与n无关,n越大,误差越小
例题 g(x)=1/(1+x^2),-6<=x<6,采用分段线性插值法求插值
- x=linspace(-6,6,100);
- y=1./(1+x.^2);
- x1=linspace(-6,6,5);
- y1=1./(1+x1.^2);
- plot(x,y,x1,y1,x1,y1,'o','LineWidth',1.5),
- gtext('n=4'),
3、样条插值:比分段插值更加光滑,在数学上,光滑程度的定量描述是:函数(曲线)的k阶导数存在且连续,则称该曲线具有k接光滑性/
光滑性的阶次越高,则越光滑。而三次样条插值就是一个较低次的分段多项式达到较高阶光滑性的典型例子!
3、用MATLAB作插值计算(重点)
一维插值函数:
yi=interp1(x,y,xi,'method')
yi表示xi处的插值结果
x、y表示插值节点
xi表示被插值点
'method'表示插值方法:
'nearest' 最近临近插值
'linear' 线性插值
'spilne' 三次样条插值
'cubic' 立方插值
缺省时默认采用分段线性插值
例题 从1点到12点的11个小时内,每个1小时测量一次温度,测得的温度数值依次为5,8,9,15,25,29,31,30,22,25,27,24,试估计每隔1/10消失的温度值
- x=1:12;
- y=[5 8 9 15 25 29 31 30 22 25 27 24];
- xi=1:0.1:12;
- yi=interp1(x,y,xi,'spline');
- plot(x,y,'+',xi,yi,x,y,'r:')
- xlabel('小时'),ylabel('温度')
例 在车辆行驶中,从驾驶员看到障碍物开始,到作出判断而采取制动措施停车所需的最短距离叫停车视距,停车视距由三部分组成:一是驾驶员反应时间内行驶的距离(即反应距离);三是开始制动到车辆完全停止所行驶的距离(即制动距离);三是车辆停止时与障碍物应该保持的安全距离。其中,制动距离主要与行驶速度和路面类型有关。根据测试,某型年辆在潮湿天气于沥青路面行驶时,其行车速度(单位:km/h) 与制动距离(单位:m)的关系如下表所示.
| 速度 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 |
| 制动距离 | 3.15 | 7.08 | 12.59 | 19.68 | 28.34 | 38.57 | 50.4 | 63.75 | 78.71 | 95.22 | 113.29 | 132.93 | 154.12 | 176.87 |
假设驾驶员的反应时间为10s,安全距离为10m。请问(1)根据某驾驶员的实际视力和视觉习惯,其驾驶时的有效视距为120m,则其在该路面行车时,时速最高不能超过多少?(结果取整)(2)若以表中数据参考,设计一条最高时速为125km/h的高速公路,则设计人员应该保证驾驶者在公路上任一点的可视距离为多少米?
我们设速度为v,停车视距为d,反应距离为d1,制动距离为d2,安全距离为d3,已知反应时间为10s,安全距离为10m,则:10v+d2+10=120
- v=20:10:150;
- vs=v.*(1000/3600);
- d1=10.*vs;
- d2=[3.15,7.08,12.59,19.68,28.34,38.57,50.4,63.75,78.71,95.22,113.29,132.93,154.12,176.87];
- d3=10;
- d=d1+d2+d3;
- vi=20:1:150;
- di=interp1(v,d,vi,'spline');
- x=abs(di-120);
- [y,i]=sort(x);
- vi(i(1))
- plot(vi,di,vi(i(1)),di(i(1)),'rp')
- j=find(vi==125);
- di(j)
二、二位插值
二位插值我们就不再细讲了,讲一下如何用matlab来计算即可
用MATLAB作网格节点数据的插值
z=interp2(x0,y0,z0,x,y,'method')
其中x0、y0、z0表示插值节点
x、y表示被插值点
z表示被插值点的函数值
'method'表示插值方法
例题 测得在平板表面3*5网格点处的温度分别为:
82 81 80 82 84
79 63 61 65 81
84 84 82 85 86
试作出平板表面的温度分布曲面z=f(x,y)的图形
- x=1:5;
- y=1:3;
- temps=[82 81 80 82 84;79 63 61 65 81;84 84 82 85 86];
- mesh(x,y,temps)
- pause
- xi=1:0.2:5;
- yi=1:0.2:3;
- zi=interp2(x,y,temps,xi,yi,'cubic');
- mesh(xi,yi,zi)
数据导入
xlsread('filename',n,'al:bl')
数据残缺、异常数据
新建实时脚本 - 导入数据 - 任务 - 清理缺失(清理离群)
三、拟合(最小二乘法)
拟合问题引例 已知热敏电阻数据:
| 温度t(摄氏度) | 20.5 | 32.7 | 51.0 | 73.0 | 95.7 |
| 电阻R( | 765 | 826 | 873 | 942 | 1032 |
求60摄氏度时的电阻
设R=at+b,a,b为待定系数
曲线拟合问题的提法:已知一组(二维数据),即平面上n个点(,
)i,···,你,寻求一个函数(曲线)y=f(x),使f(x)在某种准则下与所有数据点最为接近,即曲线拟合的最好。
插值和拟合的关系:
问题:给定一批数据点,需要确定满足特定要求的曲线或曲面
解决方案:
·若要求所求曲线(面)通过所给特定数据点,就是插值问题;
·若不要求曲线(面)通过所有数据点,而是要求它反映对象整体的变化趋势,这就是数据拟合,又称曲线拟合或曲面拟合。
二者区别:
·插值试图去通过已知点了解未知点处的函数值;
·拟合则在于整体上用某种已知函数去拟合数据点列所在未知函数的状态。
·关键区别在于插值要求必须经过已知点列,拟合只求尽量靠近不必经过!
用MATLAB解决线性拟合问题
线性最小二乘法
polyfit(x,y,m)
x、y表示输入同长度的数组
m表示拟合多项式次数
a表示输出拟合多项式系数
a=[
,...,
,
]
z=polyval(a,x)来算多项式在x处的值
非线性最小二乘拟合
MATLAB提供了两个求非线性最小二乘拟合的函数:lsqcurvefit和lsqnonlin。两个命令都要先建立M文件fun.m,在其中定义函数f(x),但两者定义f(x)的方式是不同的。
1、lsqcurvefit('fit',x0,xdata,ydata,options);
fun是一个实现建立的定义函数F(x,xdata)的M文件,自变量为x和xdata
x0表示迭代初值
options表示选项见无约束优化
2、lsqnonlin('fun',x0,options);
同上
MATLAB解应用问题实例
1、电阻问题
例 由数据
| 温度t(摄氏度) | 20.5 | 32.7 | 51.0 | 73.0 | 95.7 |
| 电阻R( | 765 | 826 | 873 | 942 | 1032 |
来拟合y=ax+b;用命令:polyfit(x,y,m)
- t=[20.5 32.5 51 73 95.7];
- r=[765 826 873 942 1032];
- n=polyfit(t,r,1);
- a=n(1)
- b=n(2)
- y=polyval(n,t);
- plot(t,r,'k+',t,y,'r')
2、水塔流量估计问题
某居民区有一供居民用水的圆柱形水塔,一般可以通过测量其水位来估计水的流量,但面临的困难是,当水塔水位下降到设定的最低水位时,水泵自动启动向水塔供水,到设定的最高水位时停止供水,这段时间无法测量水塔的水位和水泵的供水量.通常水泵每天供水一两次,每次约两小时.
水塔是一个高12.2m,直径17.4m的正圆柱.按照设计,水塔水位降至约8.2m时,水泵自动启动,水位升到约10.8m时水泵停止工作.
表1是某一天的水位测量记录,试估计任何时刻(包括水泵正供水时)从水塔流出的水流量,及一天的总用水量.(符号//表示水泵启动)
| 时刻(h) | 0 | 0.92 | 1.84 | 2.95 | 3.87 | 4.98 | 5.90 | 7.01 | 7.93 | 8.97 |
| 水位(cm) | 968 | 948 | 931 | 913 | 898 | 881 | 869 | 852 | 839 | 822 |
| 时刻(h) | 9.98 | 10.92 | 10.95 | 12.03 | 12.95 | 13.88 | 14.98 | 15.90 | 16.83 | 17.93 |
| 水位(cm) | // | // | 1082 | 1050 | 1021 | 994 | 965 | 941 | 918 | 892 |
| 时刻(h) | 19.04 | 19.96 | 20.84 | 22.01 | 22.96 | 23.88 | 24.99 | 25.91 | ||
| 水位(cm) | 866 | 843 | 822 | // | // | 1059 | 1035 | 1018 |
从测量记录看,一天有两个供水时段(以下称第1供水时段和第2供水时段),和3个水泵不工作时段(以下称第1时段 =0到 =8.97,第2次时段 =10.95到 =20.84和第3时段/23以后),对第1、2时段的测量数据直接分别作多项式拟合,得到水位函数.为使拟合曲线比较光滑,多项式次数不要太高,一般在3~6. 由于第3时段只有3个测量记录,无法对这一时段的水位作出较好的拟合
确定流量:对于第1、2时段只需将水位函数求导数即可,对于两个供水时段的流量,则用供水时段前后水泵(不工作时段)的流量拟合得到,并且将拟合得到的第2供水时段流量外推,将第3时段流量包含在第2供水时段内.
一天总用水量的估计:总用水量等于两个水泵不工作时段和两个时段用水量之和,他们都可以由流量对时间积分得到
这个问题是相对比较复杂的,我们这里只给出结果,计算就交给大家



