- 1什么是SAP HANA?
- 2android新建项目报错:Error Could not open proj remapped class cache for 8y6fc
- 3数据结构专题——二叉树
- 4zookeeper的启动和状态查看
- 5【抓包教程】BurpSuite联动雷电模拟器——安卓高版本抓包移动应用教程_雷电模拟器burpsuite抓包
- 6AIGC的发展
- 7Linux配置PX4时运行git submodule update --init --recursive命令出现如下错误:fatal: 远端意外挂断了fatal: 过早的文件结束符(EOF)的解决办法_fatal: 远端意外挂断了 fatal: 过早的文件结束符(eof) fatal: 无法读取远程仓
- 8java中集合List,Set,Queue,Map
- 9spark sql 总结
- 10最牛逼的编程语言,没有之一
遗传算法总结_遗传算法的实验总结
赞
踩
1、不适用的场合:比如破解密码这种,答案非对即错,只有两种可能,没有连续的逐步逼近的过程的场合。
2、原理及举例①:
链接:https://www.zhihu.com/question/23293449/answer/120185075
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
这是个真实的故事。
从前在海岸边有一群扇贝在悠哉游哉地生活繁衍着。它们自然是衣食不愁,连房子也有了着落。它们担忧的只有一件事:每隔一段时间,总有一个人来挖走它们之中的一部分。当然啦,挖回去干什么这大家都知道。但扇贝们不知道的是,这人的家族图腾是Firefox的图标,所以他总是选择那些贝壳花纹长得比较不像Firefox图标的扇贝。
这种状况持续了好几十万代。大家应该也猜到扇贝们身上发生什么事情了:它们的贝壳上都印着很像Firefox图标的图案。
可能有些读者会说:你这不是糊弄我们么,Firefox才有多少年历史,你就搞了个几十万代的扇贝?
确有其事,但是这些扇贝不是真实的,它们在我电脑的内存里边生活。它们是一个遗传算法程序的一部分,这个程序的目的就是用100个半透明三角形把Firefox的图标尽可能像地画出来。
什么是遗传算法呢?
简单地说,遗传算法是一种解决问题的方法。它模拟大自然中种群在选择压力下的演化,从而得到问题的一个近似解。
在二十世纪五十年代,生物学家已经知道基因在自然演化过程中的作用了,而他们也希望能在新出现的计算机上模拟这个过程,用以尝试定量研究基因与进化之间的关系。这就是遗传算法的滥觞。后来,有人将其用于解决优化问题,于是就产生了遗传算法。
那么,具体来说,在计算机里边是怎么模拟进化过程的呢?
我们还是以开头提到的程序为例。
首先,我们知道,生物个体长什么样子很大程度上是由染色体上的基因决定的。同样,如果我们把100个半透明三角形组成的东西看成一个生物个体的话(为了说话方便,称为扇贝吧),我们也可以说它的样子是由这些三角形的具体位置和颜色决定的。所以,我们可以把一个一个的半透明三角形看作是这些扇贝的“基因”。而组成扇贝的这100个基因就组成了每个扇贝个体的“染色体”(chromosome)。
从下面的图可以大约看出来这些基因是怎么决定扇贝的样子的(为了观看方便,我们只画出其中五个三角形):
<img src="https://pic1.zhimg.com/50/86e744064db3b2d49acee003d88b0b32_hd.jpg" data-rawheight="95" data-rawwidth="482" class="origin_image zh-lightbox-thumb" width="482" data-original="https://pic1.zhimg.com/86e744064db3b2d49acee003d88b0b32_r.jpg">
然后,扇贝们除了生活,当然还要繁衍后代。生物界中的繁衍无非就是父母的基因组合产生新的个体,而在这个程序里边我们当然也这么办:选择两个原有的扇贝,然后从这两个扇贝的染色体中随机选取一共100个基因组成新个体的染色体。如图所示:(仍然是将扇贝看成是五个三角形组成的)
<img src="https://pic4.zhimg.com/50/219255ed582319e0df3c3b1974b4cb5d_hd.jpg" data-rawheight="387" data-rawwidth="510" class="origin_image zh-lightbox-thumb" width="510" data-original="https://pic4.zhimg.com/219255ed582319e0df3c3b1974b4cb5d_r.jpg">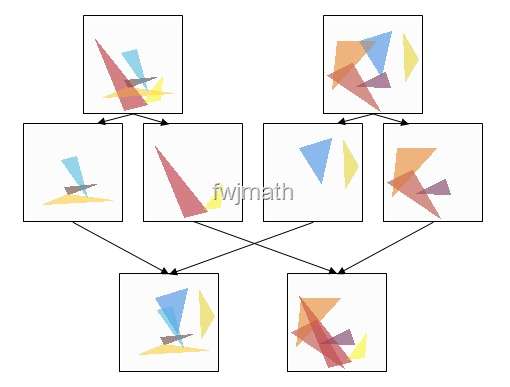
为了产生新的基因,使基因的种类更多样化,在组合的时候,新的扇贝的基因有一定的概率发生变异。也就是说,其中的一个透明三角形的位置或者颜色会随机改变,如图(仍然是五个三角形……我偷工减料……):
<img src="https://pic1.zhimg.com/50/7031d0fb6f2f222970339e5acb649235_hd.jpg" data-rawheight="121" data-rawwidth="285" class="content_image" width="285">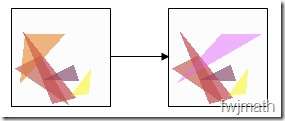
其次,为了使扇贝的样子向Firefox图标靠近,我们要给它们加上一点选择压力,就是文章开头故事中提到的那个人的行动:在每一代把最不像Firefox的扇贝淘汰出去,同时也给新的个体留下生存的空间。怎么评价这个扇贝像不像Firefox呢?最直接的方法就是一个一个像素比较,颜色相差得越多就越不像。这个评价的函数叫做“适应函数”,它负责评价一个个体到底有多适应我们的要求。
在淘汰的过程中,为了便于编程,我们通常会在淘汰旧个体和产生新个体的数目上进行适当的调整,使种群的大小保持不变。淘汰的作用就是使适应我们要求的个体存在的时间更长,从而达到选择的目的。
最后,在自然界中,种群的演化是一个无休止的过程,但程序总要停下来给出一个结果。那么,什么时候终止演化输出结果呢?这就要订立一个终止条件,满足这个条件的话程序就输出当前最好的结果并停止。最简单的终止条件就是,如果种群经过了很多代(这里的“很多”是一个需要设定的参数)之后仍然没有显着改变适应性的变异的话,我们就停止并输出结果。我们就用这个终止条件。
好了,现在是万事俱备只欠东风了。定义好基因,写好繁衍、变异、评价适应性、淘汰和终止的代码之后,只需要随机产生一个适当大小的种群,然后让它这样一代代的繁衍、变异和淘汰下去,到最后终止我们就会获得一个惊喜的结果:(这回是完整的了,图片下的数字表示这个扇贝是第几代中最好的)
<img src="https://pic3.zhimg.com/50/467623b900370eaafc771b5deaf15a23_hd.jpg" data-rawheight="480" data-rawwidth="469" class="origin_image zh-lightbox-thumb" width="469" data-original="https://pic3.zhimg.com/467623b900370eaafc771b5deaf15a23_r.jpg">
怎么样?虽说细节上很欠缺,但是也算是不错了。要不,你来试试用100个透明三角形画一个更像的?就是这样的看上去很简单的模拟演化过程也能解决一些我们这些有智慧的人类也感到棘手的问题。
实际上,在生活和生产中,很多时候并不需要得到一个完美的答案;而很多问题如果要得到完美的答案的话,需要很大量的计算。所以,因为遗传算法能在相对较短的时间内给出一个足够好能凑合的答案,它从问世伊始就越来越受到大家的重视,对它的研究也是方兴未艾。当然,它也有缺点,比如说早期的优势基因可能会很快通过交换基因的途径散播到整个种群中,这样有可能导致早熟(premature),也就是说整个种群的基因过早同一化,得不到足够好的结果。这个问题是难以完全避免的。
其实,通过微调参数和繁衍、变异、淘汰、终止的代码,我们有可能得到更有效的算法。遗传算法只是一个框架,里边具体内容可以根据实际问题进行调整,这也是它能在许多问题上派上用场的一个原因。像这样可以适应很多问题的算法还有模拟退火算法、粒子群算法、蚁群算法、禁忌搜索等等,统称为元启发式算法(Meta-heuristic algorithms)。
另外,基于自然演化过程的算法除了在这里说到的遗传算法以外,还有更广泛的群体遗传算法和遗传编程等,它们能解决很多棘手的问题。这也从一个侧面说明,我们不一定需要一个智能才能得到一个构造精巧的系统。
无论如何,如果我们要将遗传算法的发明归功于一个人的话,我会将它归功于达尔文,进化论的奠基人。如果我们不知道自然演化的过程,我们也不可能在电脑中模拟它,更不用说将它应用于实际了。
向达尔文致敬!
3、原理及举例②、
链接:https://www.zhihu.com/question/23293449/answer/120220974
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
大三的时候上了一门人工智能,其中有一次作业就用到了遗传算法,问题是这样的:
求解函数 f(x) = x + 10*sin(5*x) + 7*cos(4*x) 在区间[0,9]的最大值。
这个函数大概长这样:
<img src="https://pic7.zhimg.com/50/c461e04cdc0b8947bad5f1a47fc322e6_hd.jpg" data-caption="" data-size="normal" data-rawwidth="1266" data-rawheight="932" class="origin_image zh-lightbox-thumb" width="1266" data-original="https://pic7.zhimg.com/c461e04cdc0b8947bad5f1a47fc322e6_r.jpg">
那么如何应用遗传算法如何来找到这个奇怪的函数的最大值呢?
事实上,不管一个函数的形状多么奇怪,遗传算法都能在很短的时间内找到它在一个区间内的(近似)最大值。
相当神奇,不是吗?
接下来围绕这个问题,讲讲我对遗传算法的一些理解。实现代码以及在Matlab中使用遗传算法的小教程都附在最后。
1.介绍
遗传算法(Genetic Algorithm)遵循『适者生存』、『优胜劣汰』的原则,是一类借鉴生物界自然选择和自然遗传机制的随机化搜索算法。
遗传算法模拟一个人工种群的进化过程,通过选择(Selection)、交叉(Crossover)以及变异(Mutation)等机制,在每次迭代中都保留一组候选个体,重复此过程,种群经过若干代进化后,理想情况下其适应度达到***近似最优***的状态。
自从遗传算法被提出以来,其得到了广泛的应用,特别是在函数优化、生产调度、模式识别、神经网络、自适应控制等领域,遗传算法发挥了很大的作用,提高了一些问题求解的效率。
2.遗传算法组成
- 编码 -> 创造染色体
- 个体 -> 种群
- 适应度函数
- 遗传算子
- 选择
- 交叉
- 变异
- 运行参数
- 是否选择精英操作
- 种群大小
- 染色体长度
- 最大迭代次数
- 交叉概率
- 变异概率
2.1 编码与解码
实现遗传算法的第一步就是明确对求解问题的编码和解码方式。
对于函数优化问题,一般有两种编码方式,各具优缺点
- 实数编码:直接用实数表示基因,容易理解且不需要解码过程,但容易过早收敛,从而陷入局部最优
- 二进制编码:稳定性高,种群多样性大,但需要的存储空间大,需要解码且难以理解
对于求解函数最大值问题,我选择的是二进制编码。
<img src="https://pic4.zhimg.com/50/6f49b2e302fbebe4d3c4242495e3b1ab_hd.jpg" data-caption="" data-size="normal" data-rawwidth="706" data-rawheight="304" class="origin_image zh-lightbox-thumb" width="706" data-original="https://pic4.zhimg.com/6f49b2e302fbebe4d3c4242495e3b1ab_r.jpg">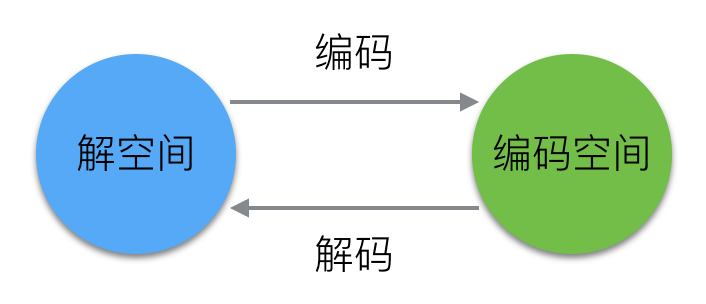
以我们的目标函数 f(x) = x + 10sin(5x) + 7cos(4x), x∈[0,9] 为例。
假如设定求解的精度为小数点后4位,可以将x的解空间划分为 (9-0)×(1e+4)=90000个等分。
2^16<90000<2^17,需要17位二进制数来表示这些解。换句话说,一个解的编码就是一个17位的二进制串。
一开始,这些二进制串是随机生成的。
一个这样的二进制串代表一条染色体串,这里染色体串的长度为17。
对于任何一条这样的染色体chromosome,如何将它复原(解码)到[0,9]这个区间中的数值呢?
对于本问题,我们可以采用以下公式来解码:
x = 0 + decimal(chromosome)×(9-0)/(2^17-1)
decimal( ): 将二进制数转化为十进制数
一般化解码公式:
- f(x), x∈[lower_bound, upper_bound]
- x = lower_bound + decimal(chromosome)×(upper_bound-lower_bound)/(2^chromosome_size-1)
lower_bound: 函数定义域的下限
upper_bound: 函数定义域的上限
chromosome_size: 染色体的长度
通过上述公式,我们就可以成功地将二进制染色体串解码成[0,9]区间中的十进制实数解。
2.2 个体与种群
『染色体』表达了某种特征,这种特征的载体,称为『个体』。
对于本次实验所要解决的一元函数最大值求解问题,个体可以用上一节构造的染色体表示,一个个体里有一条染色体。
许多这样的个体组成了一个种群,其含义是一个一维点集(x轴上[0,9]的线段)。
2.3 适应度函数
遗传算法中,一个个体(解)的好坏用适应度函数值来评价,在本问题中,f(x)就是适应度函数。
适应度函数值越大,解的质量越高。
适应度函数是遗传算法进化的驱动力,也是进行自然选择的唯一标准,它的设计应结合求解问题本身的要求而定。
2.4 遗传算子
我们希望有这样一个种群,它所包含的个体所对应的函数值都很接近于f(x)在[0,9]上的最大值,但是这个种群一开始可能不那么优秀,因为个体的染色体串是随机生成的。
如何让种群变得优秀呢?
不断的进化。
每一次进化都尽可能保留种群中的优秀个体,淘汰掉不理想的个体,并且在优秀个体之间进行染色体交叉,有些个体还可能出现变异。
种群的每一次进化,都会产生一个最优个体。种群所有世代的最优个体,可能就是函数f(x)最大值对应的定义域中的点。
如果种群无休止地进化,那总能找到最好的解。但实际上,我们的时间有限,通常在得到一个看上去不错的解时,便终止了进化。
对于给定的种群,如何赋予它进化的能力呢?
- 首先是选择(selection)
- 选择操作是从前代种群中选择***多对***较优个体,一对较优个体称之为一对父母,让父母们将它们的基因传递到下一代,直到下一代个体数量达到种群数量上限
- 在选择操作前,将种群中个体按照适应度从小到大进行排列
- 采用轮盘赌选择方法(当然还有很多别的选择方法),各个个体被选中的概率与其适应度函数值大小成正比
- 轮盘赌选择方法具有随机性,在选择的过程中可能会丢掉较好的个体,所以可以使用精英机制,将前代最优个体直接选择
- 其次是交叉(crossover)
- 两个待交叉的不同的染色体(父母)根据交叉概率(cross_rate)按某种方式交换其部分基因
- 采用单点交叉法,也可以使用其他交叉方法
- 最后是变异(mutation)
- 染色体按照变异概率(mutate_rate)进行染色体的变异
- 采用单点变异法,也可以使用其他变异方法
一般来说,交叉概率(cross_rate)比较大,变异概率(mutate_rate)极低。像求解函数最大值这类问题,我设置的交叉概率(cross_rate)是0.6,变异概率(mutate_rate)是0.01。
因为遗传算法相信2条优秀的父母染色体交叉更有可能产生优秀的后代,而变异的话产生优秀后代的可能性极低,不过也有存在可能一下就变异出非常优秀的后代。这也是符合自然界生物进化的特征的。
3.遗传算法流程
&lt;img src="https://pic4.zhimg.com/50/bbe28bbf296e4762e64867314b90bca3_hd.jpg" data-caption="" data-size="normal" data-rawwidth="1202" data-rawheight="1186" class="origin_image zh-lightbox-thumb" width="1202" data-original="https://pic4.zhimg.com/bbe28bbf296e4762e64867314b90bca3_r.jpg"&gt;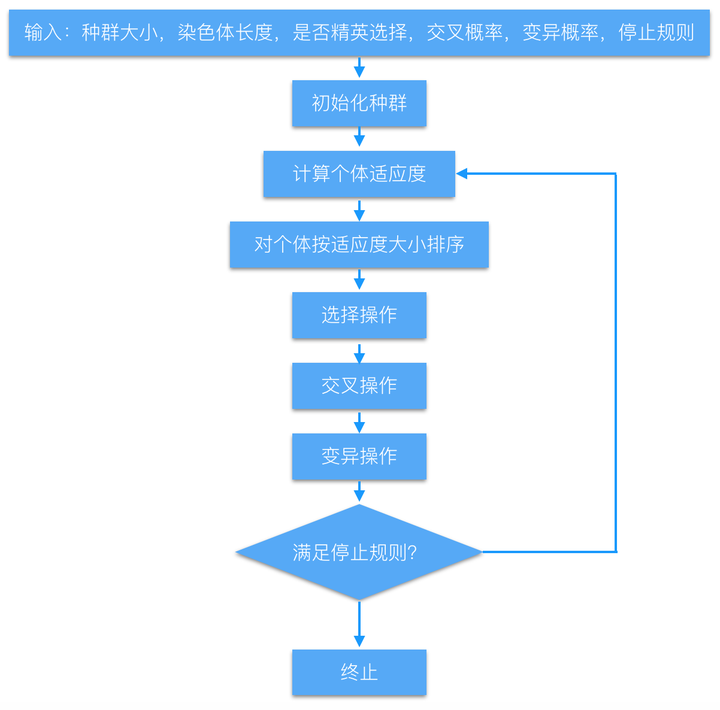
附上实现代码: genetic-algorithm
其中包含了遗传算法的 Matlab 实现和 Tensorflow 实现 (开发中)。
如果你觉得这个仓库对你有帮助,请给她一个 star 或者 fork 一下!
同时,也欢迎大家关注我的 Github 账号。
测试结果
- 最优个体:00011111011111011
- 最优适应度:24.8554
- 最优个体对应自变量值:7.8569
- 达到最优结果需要的迭代次数:多次实验后发现,达到收敛的迭代次数从20次到一百多次不等
迭代次数与平均适应度关系曲线(横轴:迭代次数,纵轴:平均适应度)
&lt;img src="https://pic1.zhimg.com/50/c4626ac1a2fea41ceb2f7face7764afe_hd.jpg" data-caption="" data-size="normal" data-rawwidth="954" data-rawheight="754" class="origin_image zh-lightbox-thumb" width="954" data-original="https://pic1.zhimg.com/c4626ac1a2fea41ceb2f7face7764afe_r.jpg"&gt;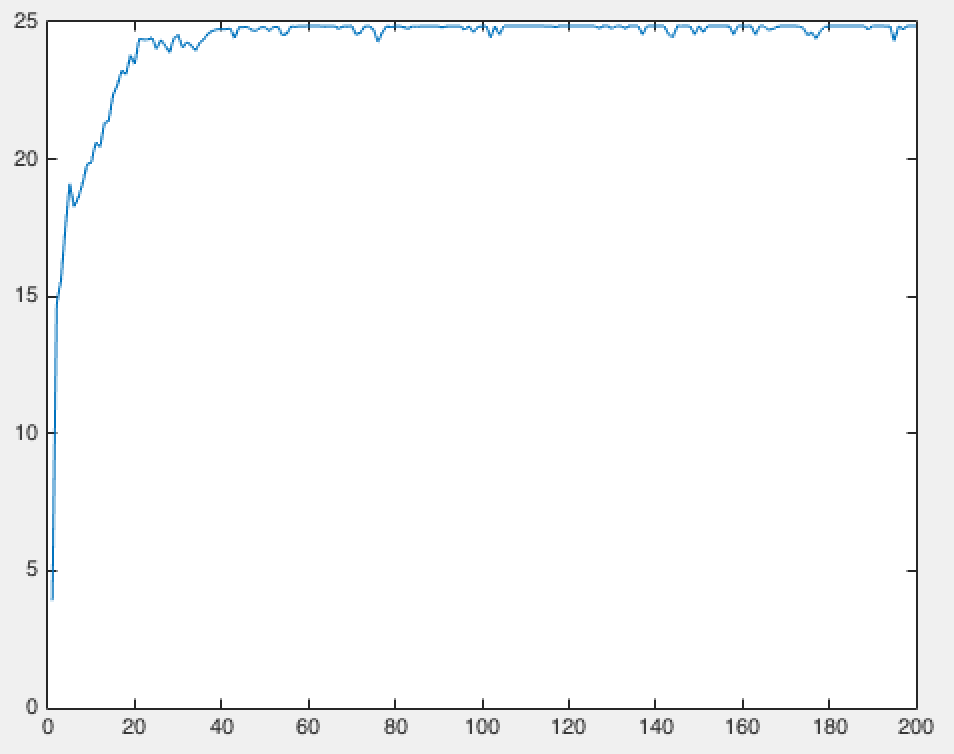
有现成的工具可以直接使用遗传算法,比如 Matlab。
最后就再介绍一下如何在 Matlab 中使用遗传算法。
在 MATLAB 中使用 GA 工具
1. 打开 Optimization 工具,在 Solver 中选择 ga - genetic algorithm,在 Fitness function 中填入@target
2. 在你的工程文件夹中新建 target.m,注意MATLAB的当前路径是你的工程文件夹所在路径
3. 在 target.m 中写下适应度函数,比如
- function [ y ] = target(x)
- y = -x-10*sin(5*x)-7*cos(4*x);
- end
*MATLAB中的GA只求解函数的(近似)最小值,所以先要将目标函数取反。
4. 打开 Optimization 工具,输入 变量个数(Number of variables) 和 自变量定义域(Bounds) 的值,点击 Start,遗传算法就跑起来了。最终在输出框中可以看到函数的(近似)最小值,和达到这一程度的迭代次数(Current iteration)和最终自变量的值(Final point)
5. 在 Optimization - ga 工具中,有许多选项。通过这些选项,可以设置下列属性
- 种群(Population)
- 选择(Selection)
- 交叉(Crossover)
- 变异(Mutation)
- 停止条件(Stopping criteria)
- 画图函数(Plot functions)
Reference
- Alex Yu ,简单遗传算法MATLAB实现
- 《机器学习》/(美)米歇尔 (Mitchell, T. M.)著;曾华军等译. —北京:机械工业出版社
链接:https://www.zhihu.com/question/23293449/answer/120102627
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
我想让机器人Bob画出我的梦中情人(最优解)。Bob当然不知道我梦中情人长啥样。
Bob很无奈,只能一张张试。先画一张,问我像不像?我说不像,Bob就重新画一张。直到我觉得像。
然而Bob又不会画画,只会填格子。于是Bob准备了一张1000*1000的格子纸,每个格子可以填黑色或者白色。那么总共有2^1000000种画法。如果我能坚持到宇宙毁灭N次,那可以每张都看,然后找到那个最像的。显然我没这个耐心。
于是我只让Bob画10万张,画不出来我就砸了它。
Bob很紧张,开始想办法,终于想到了遗传算法。
第一轮,Bob随机画了1万张(初始种群)。这1万张里面,肯定各种乱七八糟,有像星空的,像猪的,像石头的,等等。然后Bob让我挑最像的。妈蛋,我强忍怒火,挑出来一堆猪、猴、狗,好歹是哺乳动物。
Bob拿着我挑的“猪猴狗们”,如获至宝,开始第二轮,将这些画各种交叉变异一下。比如把一幅画的耳朵跟另一幅的鼻子换一下,或者再随机改个眼睛。然后又生成了1万张图让我挑。我挑出来一堆猴子猩猩,好歹是灵长类动物。
如此反复好多轮后,挑出来的开始像人了,虽然有男人、女人、小孩。
慢慢地,开始有美女了。再慢慢地,就越来越像了。
在画了10万张图后,终于找到一张还不错的。虽然不是梦中情人,但也很不错呐(次优解)。
这就是遗传算法。



