3阶常微分方程（ODE）的物理信息神经网络PINNs混合驱动解法_pinn求解常微分方程

文章目录

• • @[toc]
  • 前言：PINN在ODE中的作用
  • 一、三阶ode方程
  • • 1.1 ODE控制方程
    • 1.2 初始条件
    • 1.3 其他边界条件
  • 二、PINN求解3阶ODE方程
  • • 2.1 解析解
    • 2.2 预测效果

前言：PINN在ODE中的作用

PINN（Physics-Informed Neural Networks，物理信息神经网络）是一种结合了深度学习与物理定律的方法，特别适用于求解科学计算问题，例如偏微分方程（PDEs）和常微分方程（ODEs）。在ODE领域，PINN的作用包括但不限于以下几点：

• 解析解的逼近：PINN能够逼近那些难以找到解析解的复杂ODE的解。

• 边界条件和初始条件的整合：PINN通过在损失函数中整合ODE的边界条件和初始条件，确保了训练过程中这些条件得到满足。

• 数据驱动的解决方案：在数据稀缺或不完整的情况下，PINN结合有限的观测数据和物理定律来预测解决方案，体现了数据驱动科学的方法。

• 无网格方法：与依赖于网格划分的传统数值方法不同，PINN作为无网格方法，可以在任意点上评估解，便于处理复杂的几何和边界问题。

• 参数估计：PINN可以用于估计ODE中的未知参数，使得模型预测与观测数据最为吻合。

• 多尺度问题处理：PINN能够处理那些在传统数值方法中难以实现的多尺度或多物理问题。

• 高维问题的处理：PINN在处理高维ODE问题时，能够比传统数值方法更好地扩展，避免了“维度的诅咒”。

通过这种方式，PINN在没有充足数据的区域也能够提供符合物理定律的合理预测，这在科学和工程计算中具有重要意义。

一、三阶ode方程

1.1 ODE控制方程

$$\frac{{\partial }^{3}u(x)}{\partial x^3}=\cos (\pi x),x\in [0,10]$$

1.2 初始条件

$$u(0)=0$$

$$u(1)=\cos (\pi )=-1$$

1.3 其他边界条件

$$\frac{\partial u(1)}{\partial x}=1$$

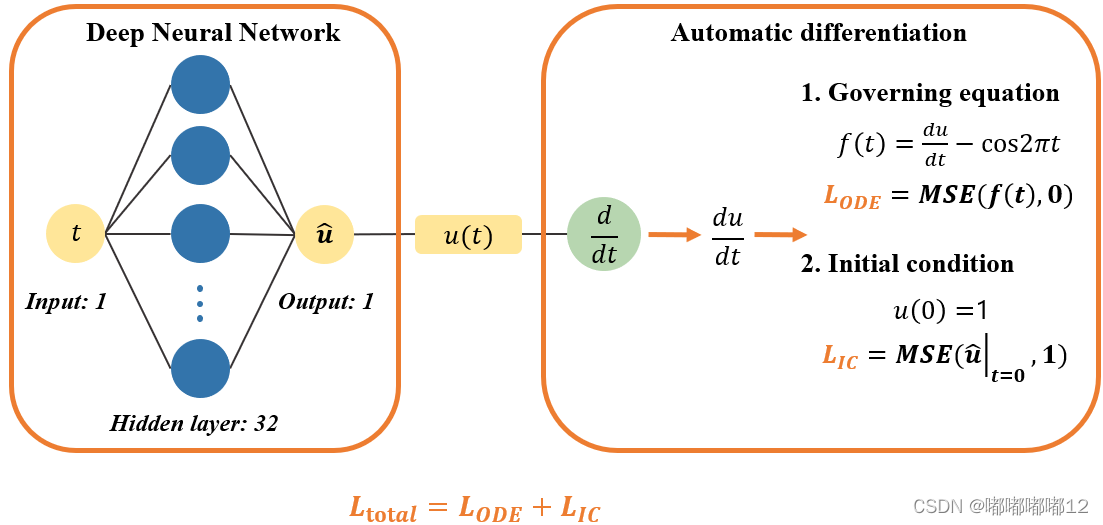
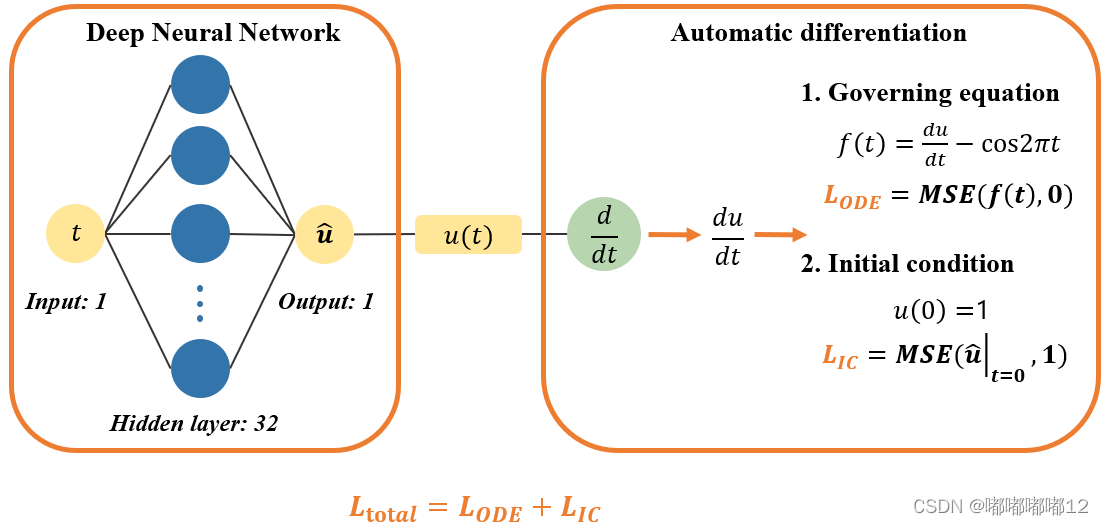
二、PINN求解3阶ODE方程

总体结构图类似如下图：

2.1 解析解

$$u(x)=\frac{\pi x(-x+({\pi }^2)(2x-3)+1)-\sin (\pi x)}{{\pi }^3}$$

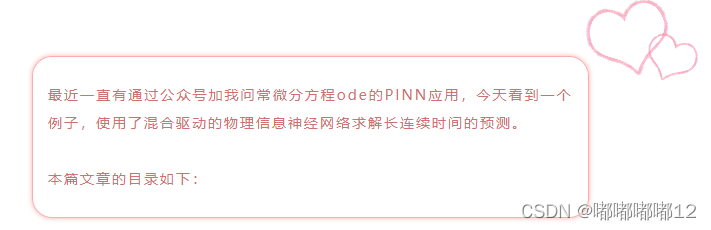
2.2 预测效果

跌代1w次，6分钟效果：

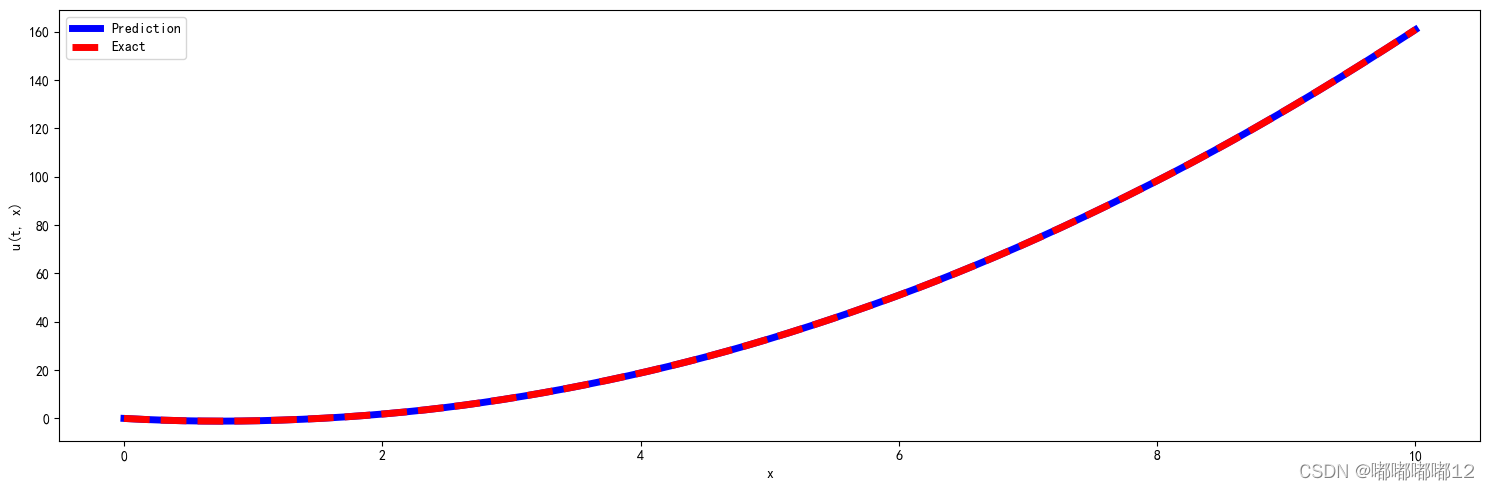
跌代1.2w次，7分钟效果：

L2误差为：0.0001716

文章来源：
3阶常微分方程（ODE）的物理信息神经网络PINNs混合驱动解法