元胞自动机（数学建模）

一.元胞自动机的概念

 

    元胞自动机(cellular automata，CA) 是一种时间、空间、状态都离散，空间相互作用和时间因果关系为局部的网格动力学模型，具有模拟复杂系统时空演化过程的能力。

    元胞自动机是用一系列模型构造的规则构成，只要满足规则就可以算作是元胞自动机模型。它是一类模型的总称、一种思想、一种方法框架。 

    CA模型的特点：①每一个元胞都取有限的离散状态；②必须遵循同样的作用规则；③依据确定的局部规则进行同步更新；④其状态改变的规则在时间和空间上都是局部的。

---

二.元胞自动机的构成

    元胞自动机最基本的组成：元胞、元胞空间、元胞邻居和元胞规则（由一个元胞空间和定义其空间的函数构成）

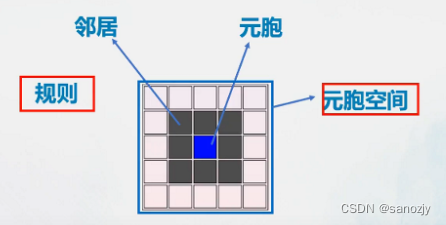
• 元胞：元胞自动机最基本的组成部分，可称为单元或基元。
• 状态： 可以是一维、二维或多维。可以是两种状态，用“生”、“死”，“0”、“1”，“黑”、“白”来表示（二进制形式）；也可以是多种状态，如不同的颜色（离散状态集）。
• 邻居：存在与某一元胞周围，能影响该元胞在下一时刻的状态。（Triangle、Square、Hexagon）
• Triangle：邻居少（3个），方便计算；但是缺少计算机的表达和显示
• Square：4个邻居；直观简单，适用于计算机环境下进行表达显示
• Hexagon：能很好模型各向同性的现象，模型更加自然现实。但是，在表达显示上不方便。
• 演化规则：根据元胞及其邻居元胞的状态，决定下一时刻该元胞状态的动力学函数，也可以是状态转移方程。 简单讲，就是状态转移函数。这个函数构造了一种简单的离散的时间和空间范围的局部物理成分。状态的变化可以由状态转移函数表示。t时刻的邻居状态组合时间元胞自动机是一个动态系统，它在时间维上的变化是离散的，即时间t是一个整数值，而且连续且等间距。在转换函数中，一个元胞在t+1时刻的状态只直接决定于t时刻的该元胞及其邻居的状态。

    邻居、元胞、元胞空间只表示系统的静态成分，所以必须添加演化规则。其规则是定义在局部空间范围内的，即一个元胞下一时刻的状态决定于本身的状态和他的邻居元胞状态。

    一维元胞自动机，用r来定义；二维元胞自动机，比较复杂，分情况确定 （4.8.27），如下图所示：

---

元胞自动机的特征：

     ①离散型：元胞自动机在时间、空间、状态上均是离散的；②同质性：服从相同的规律、分布方式相同；③并行性：元胞的状态更新规则变化是同步进行的；④高纬度：元胞自动机是一类无穷维动力系统。

元胞自动机的应用思想：

      复杂系统又称为非线性系统。传统的自顶向下的分析方法是把系统分割成几个部分，对每一个部分逐个进行研究。而目前提出来的分析复杂动态系统的思想：自底向上的研究方法。。

一维元胞自动机——交通规则

特点：

• 元胞分布于一维线性网格上.

• 元胞仅具有车和空两种状态.

• 元胞状态由周围两邻居决定.

  二维元胞自动机——生命游戏
  定义：

• 元胞分布于二维方型网格上.

• 元胞仅具有生和死两种状态.

• 元胞状态由周围八邻居决定.

• 规则：

  

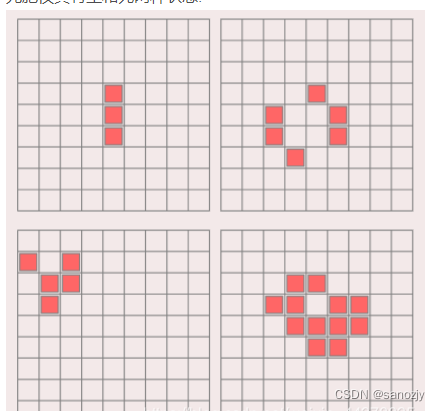
• 骷髅：死亡；笑脸：生存
  周围有三个笑脸，则中间变为笑脸；少于两个笑脸或者多于三个，中间则变死亡。

生命游戏代码（转载别人的）

%% 生命游戏
%% 界面控制
startbutton = uicontrol('style','pushbutton','string','start','fontsize',12,'position',[100,400,50,20],'callback','start=1;');
freezebutton = uicontrol('style','pushbutton','string','freeze','fontsize',12,'position',[320,400,50,20],'callback','freeze=1;');
quitebutton = uicontrol('style','pushbutton','string','quit','fontsize',12,'position',[400,400,50,20],'callback','stop=1;close;');
number = uicontrol('style','text','string','1','fontsize',12,'position',[20,400,50,20]);
freeze_at_text = uicontrol('style','text','string','freeze at：','fontsize',12,'position',[180,400,80,20],'callback','start=1;');
freeze_at = uicontrol('style','edit','string','1000','fontsize',12,'position',[250,400,50,20]);
%% 初始化设置
n = 400; % 元胞数目
z = zeros(n, n);
cells = (rand(n, n)) < 0.6; % 初始值随机分布
big_matrix = zeros(n+2, n+2); % 增补矩阵
big_matrix(2:end-1, 2:end-1) = cells;
imh = image(cat(3,z, z, cells)); % 建立图像句柄
figure(gcf);
set(gcf, 'doublebuffer', 'on'); % 开启双缓冲
%% 主循环
start = 0; stop = 0; freeze = 0;
while stop == 0
    if findobj == 0 % 用来监视窗口是否已经被关闭 防止报错
        break;
    end
    
    if start == 1
        z = zeros(n, n);
        sum = sum_neighbour(big_matrix); % 计算邻居状态和
        z(cells == 1 & (sum == 2 | sum == 3)) = 1; % 按规则更新状态
        z(cells == 0 & sum == 3) = 1;
        big_matrix(2:end-1,2:end-1) = z; % 将新状态填充回增补矩阵
        cells = z; % 将状态更新
        set(imh, 'cdata', cat(3, zeros(n,n), zeros(n,n), cells)); % 画图
        stepnumber = 1 + str2double(get(number, 'string')); % 更新计数
        set(number, 'string', num2str(stepnumber));
    end
    if (freeze == 1 || stepnumber == str2double(get(freeze_at, 'string'))) % 判断是否暂停
        start = 0;
        freeze = 0;
    end
    drawnow % 更新绘图
end
%% 计算邻居和函数
function [A] = sum_neighbour(B)
% 元胞自动机 计算周围邻居的状态和
    A = B(1:end-2,1:end-2)+B(1:end-2,2:end-1)+B(1:end-2,3:end)+B(2:end-1,1:end-2)+B(2:end-1,3:end)+B(3:end,1:end-2)+B(3:end,2:end-1)+B(3:end,3:end);
end

元胞自动机的演化行为的统计特征

元胞自动机的动力学行为归纳为四大类（Wolfram. S.，1986):

• 平稳型:自任何初始状态开始，经过一定时间运行后，元胞空间趋于一个空间平稳的构形，这里空间平稳即指每一个元胞处于固定状态。不随时间变化而变化。
• 周期型：经过一定时间运行后，元胞空间趋于一系列简单的固定结构（Stable Patterns）或周期结构（Perlodical Patterns)。由于这些结构可看作是一种滤波器（Filter），故可应用到图像处理的研究中。
• 混沌型：自任何初始状态开始，经过一定时间运行后，元胞自动机表现出混沌的非周期行为，所生成的结构的统计特征不再变止，通常表现为分形分维特征。
• 复杂型：出现复杂的局部结构，或者说是局部的混沌，其中有些会不断地传播。

另一角度，元胞自动机可视为动力系统，因而可将初始点、轨道、不动点、周期轨和终极轨等一系列概念用到元胞自动机的研究中。固定点->周期->复杂->混沌（复杂度逐渐升高）

三、NS模型

第184号原则（车辆行驶规则为：黑色元胞表示被一辆车占据，白色表示无车，若前方格子有车，则停止。若前方为空，则前进一格）

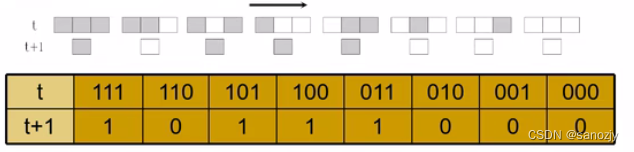
•  NS模型是一个随机CA交通流模型，每辆车的状态都由它的速度和位置所表示，其状态按照一下演化规则并进行更新：
• 

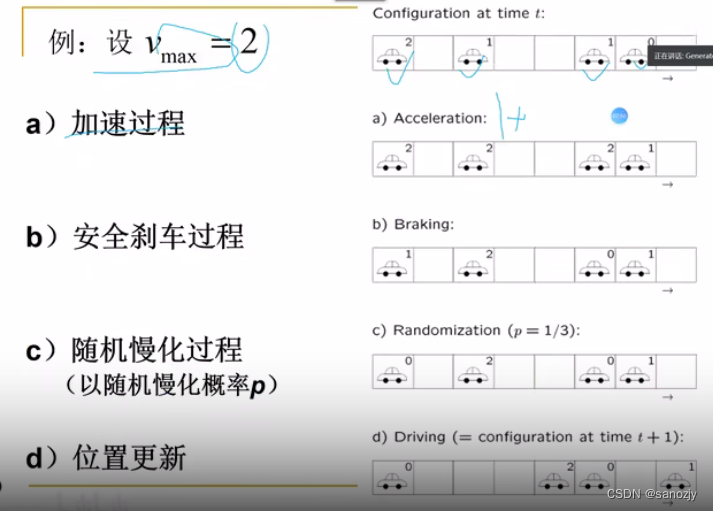
 NS模型的演化规则：

（1）加速：司机总以最大速度行驶

（2）安全刹车：避免与前车相撞

（3）随机慢化（以随机概率p）：存在不确定因素【过渡刹车、道路条件变化、心理因素、延迟加速】

（4）位置更新：车辆前进

---

 元胞自动机的优缺点

    元胞自动机在数学建模中具有以下优点和缺点：

优点：
1. 简单而直观：元胞自动机的规则通常是简单的局部交互规则，易于理解和实现。
2. 并行计算：元胞自动机的演化过程可以并行计算，适合于高性能计算和并行处理。
3. 模拟复杂系统：元胞自动机可以模拟各种复杂系统，如生物系统、社会系统和物理系统等，能够捕捉系统的自组织行为和非线性动力学。
4. 灵活性：元胞自动机可以通过调整元胞的状态和交互规则来模拟不同的系统行为，具有较高的灵活性。

缺点：
1. 精确性有限：元胞自动机是基于离散的元胞和简化的规则进行模拟，可能无法完全准确地反映真实系统的行为。
2. 参数选择困难：元胞自动机的模拟结果可能对初始条件和参数选择敏感，需要进行大量的试验和调整。
3. 计算复杂度高：对于大规模的元胞自动机模型，计算复杂度可能很高，需要消耗大量的计算资源和时间。
4. 缺乏实证验证：元胞自动机模型通常是基于理论假设和简化的规则构建的，缺乏实证验证和实际数据的支持。