devbox
从前慢现在也慢
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

等额本金和等额本息还款方式的差异分析_如何证明等额本息还款总额大于等额本金还款总额

作者：从前慢现在也慢 | 2024-03-16 16:50:54

赞

踩

如何证明等额本息还款总额大于等额本金还款总额

我们在办理按揭贷款的时候，银行一定会问你等额本金还是等额本息的还款方式选哪一个。现在我们就定量的分析一下，这两个究竟有何差别。

等额本息还款方式

假设银行年利率是R,则月利率为R/12,某人贷款总额为M,还款期为20年，240个月，则按照等额本息来计算，每月还款额该多少呢？

假设每月还款为X，每期剩余还款额为Q ，当贷款下来那一刻，你还没有开始还款，所以如下公式成立：

\boldsymbol{Q_0=M}

每期的剩余本金乘以月利率，就是当月的利息,利息和本金相加，就是总欠款。第一期还款后，总欠款额为：

\boldsymbol{Q_1=Q_0 \cdot (1+\frac{R}{12})-X}

第二期还款后，本金余额为：

\boldsymbol{\\Q_2=Q_1 \cdot (1+\frac{R}{12})-X=(M \cdot (1+\frac{R}{12})-X)\cdot (1+\frac{R}{12})-X=M(1+\frac{R}{12})^2 - X((1+\frac{R}{12})+1)}

第三期还款后，本金余额为：

\boldsymbol{\\Q_3=Q_2 \cdot (1+\frac{R}{12})-X=M(1+\frac{R}{12})^3 - X((1+\frac{R}{12})^2+(1+\frac{R}{12})+1)}

递推得到如下公式（严格的说应该根据数学归纳法去证明），到达第k期还款后，剩余欠款总额为：

\boldsymbol{\\Q_k=Q_{k-1}\cdot (1+\frac{R}{12})-X=M(1+\frac{R}{12})^k - X((1+\frac{R}{12})^{k-1}+\cdots +(1+\frac{R}{12})+1)}

根据等比数列的求和公式：

\boldsymbol{\\Q_k=Q_{k-1}\cdot (1+\frac{R}{12})-X=M(1+\frac{R}{12})^k - X((1+\frac{R}{12})^{k-1}+\cdots +(1+\frac{R}{12})+1)}

\boldsymbol{\\Q_k=M(1+\frac{R}{12})^k - X((1+\frac{R}{12})^{k-1}+\cdots +(1+\frac{R}{12})+1)=M(1+\frac{R}{12})^k - \frac{1-(1+\frac{R}{12})^k}{1-(1+\frac{R}{12})}\cdot X}

当Q_k=0的时候，还款完毕，所以：

M(1+\frac{R}{12})^k = \frac{1-(1+\frac{R}{12})^k}{1-(1+\frac{R}{12})}\cdot X=\frac{(1+\frac{R}{12})^k-1}{\frac{R}{12}}\cdot X

所以，等额本息情况下，每月还款金额为：

\\X=\frac{M\cdot \frac{R}{12 }\cdot (1+\frac{R}{12})^k}{(1+\frac{R}{12})^k-1}=\boldsymbol{M\cdot\frac{ \frac{R}{12 }\cdot (1+\frac{R}{12})^k}{(1+\frac{R}{12})^k-1}}

这个公式也就是大家常见到的等额本息还款计算方式的文字描述版：

用年利率表示就是下面的公式：

本金额和利息额

每月均还X元，这X元有多少本金和利息呢？第一个月的利息和剩余本金为：

\\ \boldsymbol{S_1=M\cdot\frac{R}{12}=M\cdot \frac{R}{12}\cdot (\frac{R}{12}+1)^0-X(\frac{R}{12}+1)^0+X} \\\boldsymbol{B_1=X-S_1=X-M\cdot\frac{R}{12}=X(\frac{R}{12}+1)^0-M\cdot\frac{R}{12}\cdot(\frac{R}{12}+1)^0}

依次计算，寻找规律：

\\\boldsymbol{S_2=(M-B_1)\cdot\frac{R}{12}=(M-X+M\cdot\frac{R}{12})\cdot \frac{R}{12}=M\cdot[(\frac{R}{12})^2+\frac{R}{12}]-X\cdot \frac{R}{12} = M\cdot \frac{R}{12}\cdot (\frac{R}{12}+1)^1-X(\frac{R}{12}+1)^1+X} \\ \boldsymbol{B_2= X-S_2=X(\frac{R}{12}+1)^1-M\cdot\frac{R}{12}\cdot(\frac{R}{12}+1)^1}

。。。。。。

规律已经很明显了，总结归纳得到,经过k期后，下一期的本金额和利息额计算公式分别为：

\\\boldsymbol{S_k = M\cdot \frac{R}{12}\cdot (\frac{R}{12}+1)^{k-1}-X(\frac{R}{12}+1)^{k-1}+X} \\ \boldsymbol{B_{k}= X-S_{k}=X(\frac{R}{12}+1)^{k-1}-M\cdot\frac{R}{12}\cdot(\frac{R}{12}+1)^{k-1}}

并且，下面的公式永远成立：

\boldsymbol{S_k+B_k = X}

以上是通过归纳看出来的，本着严谨至上的原则，我们还是来证明一把，就用数学归纳法。

假设K的时候等式成立

\\\boldsymbol{S_k = M\cdot \frac{R}{12}\cdot (\frac{R}{12}+1)^{k-1}-X(\frac{R}{12}+1)^{k-1}+X} \\ \boldsymbol{B_{k}= X-S_{k}=X(\frac{R}{12}+1)^{k-1}-M\cdot\frac{R}{12}\cdot(\frac{R}{12}+1)^{k-1}}

则k+1时：

\boldsymbol{S_{k+1}=(M-B_1-B_2-\cdots-B_{k-1}-B_{k})\cdot \frac{R}{12}=(M-B_1-B_2-\cdots-B_{k-1})\cdot \frac{R}{12}-B_{k}\cdot\frac{R}{12}=S_k-B_k\cdot\frac{R}{12}}

带入上式：

\mathbf{S_{k+1}=S_k-B_k\cdot\frac{R}{12}=M\cdot \frac{R}{12}\cdot (\frac{R}{12}+1)^{k-1}-X(\frac{R}{12}+1)^{k-1}+X -[X(\frac{R}{12}+1)^{k-1}-M\cdot\frac{R}{12}\cdot(\frac{R}{12}+1)^{k-1}] \cdot \frac{R}{12}}

简单的合并同类项:

\boldsymbol{S_{k+1}=S_k-B_k\cdot\frac{R}{12}=M\cdot \frac{R}{12}\cdot (\frac{R}{12}+1)^{k-1}(\frac{R}{12}+1)-X(\frac{R}{12}+1)^{k-1}(\frac{R}{12}+1)+X}

所以，最终得到一样的形式：

\boldsymbol{S_{k+1}=S_k-B_k\cdot\frac{R}{12}=M\cdot \frac{R}{12}\cdot (\frac{R}{12}+1)^{k}-X(\frac{R}{12}+1)^{k}+X}

\boldsymbol{B_{k+1}= X-S_{k+1}=X(\frac{R}{12}+1)^{k}-M\cdot\frac{R}{12}\cdot(\frac{R}{12}+1)^{k}}

上述经验总结公式得证.

对于等额本息的还款公式，总结如下：

每月还款额计算公式：

\\X=\boldsymbol{M\cdot\frac{ \frac{R}{12 }\cdot (1+\frac{R}{12})^k}{(1+\frac{R}{12})^k-1}}

当月利息额计算公式：

\boldsymbol{S_k = M\cdot \frac{R}{12}\cdot (\frac{R}{12}+1)^{k-1}-X(\frac{R}{12}+1)^{k-1}+X}

当月本金额的计算公式:

\boldsymbol{B_{k}= X-S_{k}=X(\frac{R}{12}+1)^{k-1}-M\cdot\frac{R}{12}\cdot(\frac{R}{12}+1)^{k-1}}

编程验证

以贷款100万，期限20年，年利率为4.6%来计算，套用如上公式，编程得到每月还款金额为6380.600586元，每月的利息和本金额打印所示，根据银行的计算器实际验证，是完全吻合的。

  1. #include <stdio.h>
  2. #include <stdlib.h>
  3. #include <math.h>
  4.  
  5. int main(void)
  6. {
  7. 	int i = 1;
  8. 	float x = 1000000 *(0.046 / 12)*pow((0.046/12 + 1), 240)/(pow((0.046/12 + 1), 240) - 1);
  9.  
  10. 	for(i = 1; i <= 240; i ++)
  11. 	{
  12. 		float sk = 1000000 * 0.046/12*pow((0.046/12 + 1), i-1) - x*pow((0.046/12 + 1), i-1) + x;
  13. 		float bk = x- sk;
  14.  
  15. 		printf("NO[%3d]: sk = %f, bk = %f, sk + bk = %f, interst ratio %f.\n", i, sk, bk, sk+bk, sk/x);
  16. 	}
  17.  
  18. 	return 0;
  19. }
  1. caozilong@caozilong-Vostro-3268:~/Workspace/yinhang$ ./a.out 
  2. NO[001]: sk = 3833.333252, bk = 2547.267334, sk + bk = 6380.600586, interst ratio 0.600779.
  3. NO[002]: sk = 3823.568848, bk = 2557.031738, sk + bk = 6380.600586, interst ratio 0.599249.
  4. NO[003]: sk = 3813.766846, bk = 2566.833740, sk + bk = 6380.600586, interst ratio 0.597713.
  5. NO[004]: sk = 3803.927246, bk = 2576.673340, sk + bk = 6380.600586, interst ratio 0.596171.
  6. NO[005]: sk = 3794.050049, bk = 2586.550537, sk + bk = 6380.600586, interst ratio 0.594623.
  7. NO[006]: sk = 3784.135010, bk = 2596.465576, sk + bk = 6380.600586, interst ratio 0.593069.
  8. NO[007]: sk = 3774.181885, bk = 2606.418701, sk + bk = 6380.600586, interst ratio 0.591509.
  9. NO[008]: sk = 3764.190674, bk = 2616.409912, sk + bk = 6380.600586, interst ratio 0.589943.
  10. NO[009]: sk = 3754.160889, bk = 2626.439697, sk + bk = 6380.600586, interst ratio 0.588371.
  11. NO[010]: sk = 3744.093018, bk = 2636.507568, sk + bk = 6380.600586, interst ratio 0.586793.
  12. NO[011]: sk = 3733.986328, bk = 2646.614258, sk + bk = 6380.600586, interst ratio 0.585209.
  13. NO[012]: sk = 3723.841064, bk = 2656.759521, sk + bk = 6380.600586, interst ratio 0.583619.
  14. NO[013]: sk = 3713.656738, bk = 2666.943848, sk + bk = 6380.600586, interst ratio 0.582023.
  15. NO[014]: sk = 3703.433594, bk = 2677.166992, sk + bk = 6380.600586, interst ratio 0.580421.
  16. NO[015]: sk = 3693.170898, bk = 2687.429688, sk + bk = 6380.600586, interst ratio 0.578812.
  17. NO[016]: sk = 3682.869141, bk = 2697.731445, sk + bk = 6380.600586, interst ratio 0.577198.
  18. NO[017]: sk = 3672.527832, bk = 2708.072754, sk + bk = 6380.600586, interst ratio 0.575577.
  19. NO[018]: sk = 3662.146973, bk = 2718.453613, sk + bk = 6380.600586, interst ratio 0.573950.
  20. NO[019]: sk = 3651.726318, bk = 2728.874268, sk + bk = 6380.600586, interst ratio 0.572317.
  21. NO[020]: sk = 3641.265625, bk = 2739.334961, sk + bk = 6380.600586, interst ratio 0.570678.
  22. NO[021]: sk = 3630.764648, bk = 2749.835938, sk + bk = 6380.600586, interst ratio 0.569032.
  23. NO[022]: sk = 3620.223633, bk = 2760.376953, sk + bk = 6380.600586, interst ratio 0.567380.
  24. NO[023]: sk = 3609.642334, bk = 2770.958252, sk + bk = 6380.600586, interst ratio 0.565721.
  25. NO[024]: sk = 3599.020264, bk = 2781.580322, sk + bk = 6380.600586, interst ratio 0.564057.
  26. NO[025]: sk = 3588.357422, bk = 2792.243164, sk + bk = 6380.600586, interst ratio 0.562385.
  27. NO[026]: sk = 3577.654053, bk = 2802.946533, sk + bk = 6380.600586, interst ratio 0.560708.
  28. NO[027]: sk = 3566.909424, bk = 2813.691162, sk + bk = 6380.600586, interst ratio 0.559024.
  29. NO[028]: sk = 3556.123535, bk = 2824.477051, sk + bk = 6380.600586, interst ratio 0.557334.
  30. NO[029]: sk = 3545.296387, bk = 2835.304199, sk + bk = 6380.600586, interst ratio 0.555637.
  31. NO[030]: sk = 3534.427734, bk = 2846.172852, sk + bk = 6380.600586, interst ratio 0.553933.
  32. NO[031]: sk = 3523.517334, bk = 2857.083252, sk + bk = 6380.600586, interst ratio 0.552223.
  33. NO[032]: sk = 3512.565186, bk = 2868.035400, sk + bk = 6380.600586, interst ratio 0.550507.
  34. NO[033]: sk = 3501.571045, bk = 2879.029541, sk + bk = 6380.600586, interst ratio 0.548784.
  35. NO[034]: sk = 3490.534668, bk = 2890.065918, sk + bk = 6380.600586, interst ratio 0.547054.
  36. NO[035]: sk = 3479.456055, bk = 2901.144531, sk + bk = 6380.600586, interst ratio 0.545318.
  37. NO[036]: sk = 3468.335205, bk = 2912.265381, sk + bk = 6380.600586, interst ratio 0.543575.
  38. NO[037]: sk = 3457.171387, bk = 2923.429199, sk + bk = 6380.600586, interst ratio 0.541825.
  39. NO[038]: sk = 3445.964844, bk = 2934.635742, sk + bk = 6380.600586, interst ratio 0.540069.
  40. NO[039]: sk = 3434.715576, bk = 2945.885010, sk + bk = 6380.600586, interst ratio 0.538306.
  41. NO[040]: sk = 3423.422852, bk = 2957.177734, sk + bk = 6380.600586, interst ratio 0.536536.
  42. NO[041]: sk = 3412.087158, bk = 2968.513428, sk + bk = 6380.600586, interst ratio 0.534760.
  43. NO[042]: sk = 3400.707764, bk = 2979.892822, sk + bk = 6380.600586, interst ratio 0.532976.
  44. NO[043]: sk = 3389.284912, bk = 2991.315674, sk + bk = 6380.600586, interst ratio 0.531186.
  45. NO[044]: sk = 3377.818115, bk = 3002.782471, sk + bk = 6380.600586, interst ratio 0.529389.
  46. NO[045]: sk = 3366.307617, bk = 3014.292969, sk + bk = 6380.600586, interst ratio 0.527585.
  47. NO[046]: sk = 3354.752686, bk = 3025.847900, sk + bk = 6380.600586, interst ratio 0.525774.
  48. NO[047]: sk = 3343.153564, bk = 3037.447021, sk + bk = 6380.600586, interst ratio 0.523956.
  49. NO[048]: sk = 3331.510010, bk = 3049.090576, sk + bk = 6380.600586, interst ratio 0.522131.
  50. NO[049]: sk = 3319.822021, bk = 3060.778564, sk + bk = 6380.600586, interst ratio 0.520299.
  51. NO[050]: sk = 3308.088867, bk = 3072.511719, sk + bk = 6380.600586, interst ratio 0.518460.
  52. NO[051]: sk = 3296.311035, bk = 3084.289551, sk + bk = 6380.600586, interst ratio 0.516615.
  53. NO[052]: sk = 3284.487793, bk = 3096.112793, sk + bk = 6380.600586, interst ratio 0.514762.
  54. NO[053]: sk = 3272.619385, bk = 3107.981201, sk + bk = 6380.600586, interst ratio 0.512901.
  55. NO[054]: sk = 3260.705566, bk = 3119.895020, sk + bk = 6380.600586, interst ratio 0.511034.
  56. NO[055]: sk = 3248.745850, bk = 3131.854736, sk + bk = 6380.600586, interst ratio 0.509160.
  57. NO[056]: sk = 3236.740479, bk = 3143.860107, sk + bk = 6380.600586, interst ratio 0.507278.
  58. NO[057]: sk = 3224.688965, bk = 3155.911621, sk + bk = 6380.600586, interst ratio 0.505390.
  59. NO[058]: sk = 3212.591309, bk = 3168.009277, sk + bk = 6380.600586, interst ratio 0.503494.
  60. NO[059]: sk = 3200.447266, bk = 3180.153320, sk + bk = 6380.600586, interst ratio 0.501590.
  61. NO[060]: sk = 3188.256592, bk = 3192.343994, sk + bk = 6380.600586, interst ratio 0.499680.
  62. NO[061]: sk = 3176.019287, bk = 3204.581299, sk + bk = 6380.600586, interst ratio 0.497762.
  63. NO[062]: sk = 3163.735107, bk = 3216.865479, sk + bk = 6380.600586, interst ratio 0.495837.
  64. NO[063]: sk = 3151.403809, bk = 3229.196777, sk + bk = 6380.600586, interst ratio 0.493904.
  65. NO[064]: sk = 3139.025146, bk = 3241.575439, sk + bk = 6380.600586, interst ratio 0.491964.
  66. NO[065]: sk = 3126.599121, bk = 3254.001465, sk + bk = 6380.600586, interst ratio 0.490016.
  67. NO[066]: sk = 3114.125488, bk = 3266.475098, sk + bk = 6380.600586, interst ratio 0.488061.
  68. NO[067]: sk = 3101.604004, bk = 3278.996582, sk + bk = 6380.600586, interst ratio 0.486099.
  69. NO[068]: sk = 3089.034668, bk = 3291.565918, sk + bk = 6380.600586, interst ratio 0.484129.
  70. NO[069]: sk = 3076.416992, bk = 3304.183594, sk + bk = 6380.600586, interst ratio 0.482152.
  71. NO[070]: sk = 3063.750977, bk = 3316.849609, sk + bk = 6380.600586, interst ratio 0.480167.
  72. NO[071]: sk = 3051.036377, bk = 3329.564209, sk + bk = 6380.600586, interst ratio 0.478174.
  73. NO[072]: sk = 3038.272949, bk = 3342.327637, sk + bk = 6380.600586, interst ratio 0.476174.
  74. NO[073]: sk = 3025.460693, bk = 3355.139893, sk + bk = 6380.600586, interst ratio 0.474165.
  75. NO[074]: sk = 3012.599365, bk = 3368.001221, sk + bk = 6380.600586, interst ratio 0.472150.
  76. NO[075]: sk = 2999.688721, bk = 3380.911865, sk + bk = 6380.600586, interst ratio 0.470126.
  77. NO[076]: sk = 2986.728516, bk = 3393.872070, sk + bk = 6380.600586, interst ratio 0.468095.
  78. NO[077]: sk = 2973.718750, bk = 3406.881836, sk + bk = 6380.600586, interst ratio 0.466056.
  79. NO[078]: sk = 2960.658936, bk = 3419.941650, sk + bk = 6380.600586, interst ratio 0.464009.
  80. NO[079]: sk = 2947.549072, bk = 3433.051514, sk + bk = 6380.600586, interst ratio 0.461955.
  81. NO[080]: sk = 2934.389160, bk = 3446.211426, sk + bk = 6380.600586, interst ratio 0.459892.
  82. NO[081]: sk = 2921.178711, bk = 3459.421875, sk + bk = 6380.600586, interst ratio 0.457822.
  83. NO[082]: sk = 2907.917480, bk = 3472.683105, sk + bk = 6380.600586, interst ratio 0.455744.
  84. NO[083]: sk = 2894.605469, bk = 3485.995117, sk + bk = 6380.600586, interst ratio 0.453657.
  85. NO[084]: sk = 2881.242676, bk = 3499.357910, sk + bk = 6380.600586, interst ratio 0.451563.
  86. NO[085]: sk = 2867.828369, bk = 3512.772217, sk + bk = 6380.600586, interst ratio 0.449461.
  87. NO[086]: sk = 2854.362793, bk = 3526.237793, sk + bk = 6380.600586, interst ratio 0.447350.
  88. NO[087]: sk = 2840.845459, bk = 3539.755127, sk + bk = 6380.600586, interst ratio 0.445232.
  89. NO[088]: sk = 2827.276367, bk = 3553.324219, sk + bk = 6380.600586, interst ratio 0.443105.
  90. NO[089]: sk = 2813.655273, bk = 3566.945312, sk + bk = 6380.600586, interst ratio 0.440970.
  91. NO[090]: sk = 2799.982178, bk = 3580.618408, sk + bk = 6380.600586, interst ratio 0.438827.
  92. NO[091]: sk = 2786.256348, bk = 3594.344238, sk + bk = 6380.600586, interst ratio 0.436676.
  93. NO[092]: sk = 2772.478027, bk = 3608.122559, sk + bk = 6380.600586, interst ratio 0.434517.
  94. NO[093]: sk = 2758.646973, bk = 3621.953613, sk + bk = 6380.600586, interst ratio 0.432349.
  95. NO[094]: sk = 2744.762695, bk = 3635.837891, sk + bk = 6380.600586, interst ratio 0.430173.
  96. NO[095]: sk = 2730.825439, bk = 3649.775146, sk + bk = 6380.600586, interst ratio 0.427989.
  97. NO[096]: sk = 2716.834473, bk = 3663.766113, sk + bk = 6380.600586, interst ratio 0.425796.
  98. NO[097]: sk = 2702.790039, bk = 3677.810547, sk + bk = 6380.600586, interst ratio 0.423595.
  99. NO[098]: sk = 2688.691895, bk = 3691.908691, sk + bk = 6380.600586, interst ratio 0.421385.
  100. NO[099]: sk = 2674.539551, bk = 3706.061035, sk + bk = 6380.600586, interst ratio 0.419167.
  101. NO[100]: sk = 2660.333008, bk = 3720.267578, sk + bk = 6380.600586, interst ratio 0.416941.
  102. NO[101]: sk = 2646.072021, bk = 3734.528564, sk + bk = 6380.600586, interst ratio 0.414706.
  103. NO[102]: sk = 2631.756348, bk = 3748.844238, sk + bk = 6380.600586, interst ratio 0.412462.
  104. NO[103]: sk = 2617.385742, bk = 3763.214844, sk + bk = 6380.600586, interst ratio 0.410210.
  105. NO[104]: sk = 2602.959961, bk = 3777.640625, sk + bk = 6380.600586, interst ratio 0.407949.
  106. NO[105]: sk = 2588.479004, bk = 3792.121582, sk + bk = 6380.600586, interst ratio 0.405680.
  107. NO[106]: sk = 2573.942627, bk = 3806.657959, sk + bk = 6380.600586, interst ratio 0.403401.
  108. NO[107]: sk = 2559.350342, bk = 3821.250244, sk + bk = 6380.600586, interst ratio 0.401114.
  109. NO[108]: sk = 2544.702393, bk = 3835.898193, sk + bk = 6380.600586, interst ratio 0.398819.
  110. NO[109]: sk = 2529.998047, bk = 3850.602539, sk + bk = 6380.600586, interst ratio 0.396514.
  111. NO[110]: sk = 2515.237305, bk = 3865.363281, sk + bk = 6380.600586, interst ratio 0.394201.
  112. NO[111]: sk = 2500.420166, bk = 3880.180420, sk + bk = 6380.600586, interst ratio 0.391878.
  113. NO[112]: sk = 2485.546143, bk = 3895.054443, sk + bk = 6380.600586, interst ratio 0.389547.
  114. NO[113]: sk = 2470.614990, bk = 3909.985596, sk + bk = 6380.600586, interst ratio 0.387207.
  115. NO[114]: sk = 2455.626709, bk = 3924.973877, sk + bk = 6380.600586, interst ratio 0.384858.
  116. NO[115]: sk = 2440.581055, bk = 3940.019531, sk + bk = 6380.600586, interst ratio 0.382500.
  117. NO[116]: sk = 2425.477783, bk = 3955.122803, sk + bk = 6380.600586, interst ratio 0.380133.
  118. NO[117]: sk = 2410.316406, bk = 3970.284180, sk + bk = 6380.600586, interst ratio 0.377757.
  119. NO[118]: sk = 2395.096924, bk = 3985.503662, sk + bk = 6380.600586, interst ratio 0.375372.
  120. NO[119]: sk = 2379.819092, bk = 4000.781494, sk + bk = 6380.600586, interst ratio 0.372977.
  121. NO[120]: sk = 2364.482910, bk = 4016.117676, sk + bk = 6380.600586, interst ratio 0.370574.
  122. NO[121]: sk = 2349.087646, bk = 4031.512939, sk + bk = 6380.600586, interst ratio 0.368161.
  123. NO[122]: sk = 2333.633545, bk = 4046.967041, sk + bk = 6380.600586, interst ratio 0.365739.
  124. NO[123]: sk = 2318.120361, bk = 4062.480225, sk + bk = 6380.600586, interst ratio 0.363308.
  125. NO[124]: sk = 2302.547363, bk = 4078.053223, sk + bk = 6380.600586, interst ratio 0.360867.
  126. NO[125]: sk = 2286.914795, bk = 4093.685791, sk + bk = 6380.600586, interst ratio 0.358417.
  127. NO[126]: sk = 2271.222412, bk = 4109.377930, sk + bk = 6380.600586, interst ratio 0.355957.
  128. NO[127]: sk = 2255.469727, bk = 4125.130859, sk + bk = 6380.600586, interst ratio 0.353489.
  129. NO[128]: sk = 2239.656738, bk = 4140.943848, sk + bk = 6380.600586, interst ratio 0.351010.
  130. NO[129]: sk = 2223.783203, bk = 4156.817383, sk + bk = 6380.600586, interst ratio 0.348523.
  131. NO[130]: sk = 2207.848633, bk = 4172.751953, sk + bk = 6380.600586, interst ratio 0.346025.
  132. NO[131]: sk = 2191.853271, bk = 4188.747070, sk + bk = 6380.600586, interst ratio 0.343518.
  133. NO[132]: sk = 2175.796387, bk = 4204.804199, sk + bk = 6380.600586, interst ratio 0.341002.
  134. NO[133]: sk = 2159.677979, bk = 4220.922852, sk + bk = 6380.600586, interst ratio 0.338476.
  135. NO[134]: sk = 2143.497559, bk = 4237.103027, sk + bk = 6380.600586, interst ratio 0.335940.
  136. NO[135]: sk = 2127.255371, bk = 4253.345215, sk + bk = 6380.600586, interst ratio 0.333394.
  137. NO[136]: sk = 2110.950928, bk = 4269.649414, sk + bk = 6380.600586, interst ratio 0.330839.
  138. NO[137]: sk = 2094.583984, bk = 4286.016602, sk + bk = 6380.600586, interst ratio 0.328274.
  139. NO[138]: sk = 2078.154297, bk = 4302.446289, sk + bk = 6380.600586, interst ratio 0.325699.
  140. NO[139]: sk = 2061.661621, bk = 4318.938965, sk + bk = 6380.600586, interst ratio 0.323114.
  141. NO[140]: sk = 2045.105591, bk = 4335.495117, sk + bk = 6380.600586, interst ratio 0.320519.
  142. NO[141]: sk = 2028.486206, bk = 4352.114258, sk + bk = 6380.600586, interst ratio 0.317915.
  143. NO[142]: sk = 2011.803101, bk = 4368.797363, sk + bk = 6380.600586, interst ratio 0.315300.
  144. NO[143]: sk = 1995.056030, bk = 4385.544434, sk + bk = 6380.600586, interst ratio 0.312675.
  145. NO[144]: sk = 1978.244751, bk = 4402.355957, sk + bk = 6380.600586, interst ratio 0.310041.
  146. NO[145]: sk = 1961.369019, bk = 4419.231445, sk + bk = 6380.600586, interst ratio 0.307396.
  147. NO[146]: sk = 1944.428711, bk = 4436.171875, sk + bk = 6380.600586, interst ratio 0.304741.
  148. NO[147]: sk = 1927.423340, bk = 4453.177246, sk + bk = 6380.600586, interst ratio 0.302076.
  149. NO[148]: sk = 1910.352905, bk = 4470.247559, sk + bk = 6380.600586, interst ratio 0.299400.
  150. NO[149]: sk = 1893.216919, bk = 4487.383789, sk + bk = 6380.600586, interst ratio 0.296715.
  151. NO[150]: sk = 1876.015259, bk = 4504.585449, sk + bk = 6380.600586, interst ratio 0.294019.
  152. NO[151]: sk = 1858.747681, bk = 4521.853027, sk + bk = 6380.600586, interst ratio 0.291312.
  153. NO[152]: sk = 1841.413940, bk = 4539.186523, sk + bk = 6380.600586, interst ratio 0.288596.
  154. NO[153]: sk = 1824.013672, bk = 4556.586914, sk + bk = 6380.600586, interst ratio 0.285869.
  155. NO[154]: sk = 1806.546753, bk = 4574.053711, sk + bk = 6380.600586, interst ratio 0.283131.
  156. NO[155]: sk = 1789.012939, bk = 4591.587891, sk + bk = 6380.600586, interst ratio 0.280383.
  157. NO[156]: sk = 1771.411865, bk = 4609.188477, sk + bk = 6380.600586, interst ratio 0.277625.
  158. NO[157]: sk = 1753.743286, bk = 4626.857422, sk + bk = 6380.600586, interst ratio 0.274856.
  159. NO[158]: sk = 1736.006958, bk = 4644.593750, sk + bk = 6380.600586, interst ratio 0.272076.
  160. NO[159]: sk = 1718.202759, bk = 4662.397949, sk + bk = 6380.600586, interst ratio 0.269285.
  161. NO[160]: sk = 1700.330200, bk = 4680.270508, sk + bk = 6380.600586, interst ratio 0.266484.
  162. NO[161]: sk = 1682.389160, bk = 4698.211426, sk + bk = 6380.600586, interst ratio 0.263673.
  163. NO[162]: sk = 1664.379272, bk = 4716.221191, sk + bk = 6380.600586, interst ratio 0.260850.
  164. NO[163]: sk = 1646.300537, bk = 4734.299805, sk + bk = 6380.600586, interst ratio 0.258017.
  165. NO[164]: sk = 1628.152344, bk = 4752.448242, sk + bk = 6380.600586, interst ratio 0.255172.
  166. NO[165]: sk = 1609.934570, bk = 4770.666016, sk + bk = 6380.600586, interst ratio 0.252317.
  167. NO[166]: sk = 1591.647095, bk = 4788.953613, sk + bk = 6380.600586, interst ratio 0.249451.
  168. NO[167]: sk = 1573.289429, bk = 4807.311035, sk + bk = 6380.600586, interst ratio 0.246574.
  169. NO[168]: sk = 1554.861328, bk = 4825.739258, sk + bk = 6380.600586, interst ratio 0.243686.
  170. NO[169]: sk = 1536.362671, bk = 4844.237793, sk + bk = 6380.600586, interst ratio 0.240787.
  171. NO[170]: sk = 1517.793091, bk = 4862.807617, sk + bk = 6380.600586, interst ratio 0.237876.
  172. NO[171]: sk = 1499.152344, bk = 4881.448242, sk + bk = 6380.600586, interst ratio 0.234955.
  173. NO[172]: sk = 1480.440186, bk = 4900.160156, sk + bk = 6380.600586, interst ratio 0.232022.
  174. NO[173]: sk = 1461.656250, bk = 4918.944336, sk + bk = 6380.600586, interst ratio 0.229078.
  175. NO[174]: sk = 1442.800293, bk = 4937.800293, sk + bk = 6380.600586, interst ratio 0.226123.
  176. NO[175]: sk = 1423.872070, bk = 4956.728516, sk + bk = 6380.600586, interst ratio 0.223156.
  177. NO[176]: sk = 1404.871216, bk = 4975.729492, sk + bk = 6380.600586, interst ratio 0.220179.
  178. NO[177]: sk = 1385.797607, bk = 4994.802734, sk + bk = 6380.600586, interst ratio 0.217189.
  179. NO[178]: sk = 1366.650879, bk = 5013.949707, sk + bk = 6380.600586, interst ratio 0.214188.
  180. NO[179]: sk = 1347.430664, bk = 5033.169922, sk + bk = 6380.600586, interst ratio 0.211176.
  181. NO[180]: sk = 1328.136841, bk = 5052.463867, sk + bk = 6380.600586, interst ratio 0.208152.
  182. NO[181]: sk = 1308.769165, bk = 5071.831543, sk + bk = 6380.600586, interst ratio 0.205117.
  183. NO[182]: sk = 1289.327148, bk = 5091.273438, sk + bk = 6380.600586, interst ratio 0.202070.
  184. NO[183]: sk = 1269.810547, bk = 5110.790039, sk + bk = 6380.600586, interst ratio 0.199011.
  185. NO[184]: sk = 1250.219238, bk = 5130.381348, sk + bk = 6380.600586, interst ratio 0.195941.
  186. NO[185]: sk = 1230.552734, bk = 5150.047852, sk + bk = 6380.600586, interst ratio 0.192858.
  187. NO[186]: sk = 1210.810913, bk = 5169.789551, sk + bk = 6380.600586, interst ratio 0.189764.
  188. NO[187]: sk = 1190.993286, bk = 5189.607422, sk + bk = 6380.600586, interst ratio 0.186658.
  189. NO[188]: sk = 1171.099854, bk = 5209.500977, sk + bk = 6380.600586, interst ratio 0.183541.
  190. NO[189]: sk = 1151.130127, bk = 5229.470703, sk + bk = 6380.600586, interst ratio 0.180411.
  191. NO[190]: sk = 1131.083740, bk = 5249.516602, sk + bk = 6380.600586, interst ratio 0.177269.
  192. NO[191]: sk = 1110.960693, bk = 5269.639648, sk + bk = 6380.600586, interst ratio 0.174115.
  193. NO[192]: sk = 1090.760376, bk = 5289.840332, sk + bk = 6380.600586, interst ratio 0.170949.
  194. NO[193]: sk = 1070.482666, bk = 5310.118164, sk + bk = 6380.600586, interst ratio 0.167771.
  195. NO[194]: sk = 1050.127197, bk = 5330.473633, sk + bk = 6380.600586, interst ratio 0.164581.
  196. NO[195]: sk = 1029.693726, bk = 5350.906738, sk + bk = 6380.600586, interst ratio 0.161379.
  197. NO[196]: sk = 1009.181885, bk = 5371.418945, sk + bk = 6380.600586, interst ratio 0.158164.
  198. NO[197]: sk = 988.591431, bk = 5392.009277, sk + bk = 6380.600586, interst ratio 0.154937.
  199. NO[198]: sk = 967.922119, bk = 5412.678711, sk + bk = 6380.600586, interst ratio 0.151698.
  200. NO[199]: sk = 947.173462, bk = 5433.427246, sk + bk = 6380.600586, interst ratio 0.148446.
  201. NO[200]: sk = 926.345337, bk = 5454.255371, sk + bk = 6380.600586, interst ratio 0.145182.
  202. NO[201]: sk = 905.437378, bk = 5475.163086, sk + bk = 6380.600586, interst ratio 0.141905.
  203. NO[202]: sk = 884.449219, bk = 5496.151367, sk + bk = 6380.600586, interst ratio 0.138615.
  204. NO[203]: sk = 863.380676, bk = 5517.219727, sk + bk = 6380.600586, interst ratio 0.135313.
  205. NO[204]: sk = 842.231323, bk = 5538.369141, sk + bk = 6380.600586, interst ratio 0.131999.
  206. NO[205]: sk = 821.000916, bk = 5559.599609, sk + bk = 6380.600586, interst ratio 0.128671.
  207. NO[206]: sk = 799.689087, bk = 5580.911621, sk + bk = 6380.600586, interst ratio 0.125331.
  208. NO[207]: sk = 778.295593, bk = 5602.305176, sk + bk = 6380.600586, interst ratio 0.121978.
  209. NO[208]: sk = 756.820129, bk = 5623.780273, sk + bk = 6380.600586, interst ratio 0.118613.
  210. NO[209]: sk = 735.262268, bk = 5645.338379, sk + bk = 6380.600586, interst ratio 0.115234.
  211. NO[210]: sk = 713.621826, bk = 5666.978516, sk + bk = 6380.600586, interst ratio 0.111842.
  212. NO[211]: sk = 691.898438, bk = 5688.702148, sk + bk = 6380.600586, interst ratio 0.108438.
  213. NO[212]: sk = 670.091736, bk = 5710.508789, sk + bk = 6380.600586, interst ratio 0.105020.
  214. NO[213]: sk = 648.201416, bk = 5732.399414, sk + bk = 6380.600586, interst ratio 0.101589.
  215. NO[214]: sk = 626.227234, bk = 5754.373535, sk + bk = 6380.600586, interst ratio 0.098145.
  216. NO[215]: sk = 604.168823, bk = 5776.431641, sk + bk = 6380.600586, interst ratio 0.094688.
  217. NO[216]: sk = 582.025818, bk = 5798.574707, sk + bk = 6380.600586, interst ratio 0.091218.
  218. NO[217]: sk = 559.797974, bk = 5820.802734, sk + bk = 6380.600586, interst ratio 0.087734.
  219. NO[218]: sk = 537.484863, bk = 5843.115723, sk + bk = 6380.600586, interst ratio 0.084237.
  220. NO[219]: sk = 515.086243, bk = 5865.514160, sk + bk = 6380.600586, interst ratio 0.080727.
  221. NO[220]: sk = 492.601776, bk = 5887.999023, sk + bk = 6380.600586, interst ratio 0.077203.
  222. NO[221]: sk = 470.031128, bk = 5910.569336, sk + bk = 6380.600586, interst ratio 0.073666.
  223. NO[222]: sk = 447.373932, bk = 5933.226562, sk + bk = 6380.600586, interst ratio 0.070115.
  224. NO[223]: sk = 424.629913, bk = 5955.970703, sk + bk = 6380.600586, interst ratio 0.066550.
  225. NO[224]: sk = 401.798676, bk = 5978.801758, sk + bk = 6380.600586, interst ratio 0.062972.
  226. NO[225]: sk = 378.879944, bk = 6001.720703, sk + bk = 6380.600586, interst ratio 0.059380.
  227. NO[226]: sk = 355.873352, bk = 6024.727051, sk + bk = 6380.600586, interst ratio 0.055774.
  228. NO[227]: sk = 332.778564, bk = 6047.822266, sk + bk = 6380.600586, interst ratio 0.052155.
  229. NO[228]: sk = 309.595245, bk = 6071.005371, sk + bk = 6380.600586, interst ratio 0.048521.
  230. NO[229]: sk = 286.323059, bk = 6094.277344, sk + bk = 6380.600586, interst ratio 0.044874.
  231. NO[230]: sk = 262.961670, bk = 6117.638672, sk + bk = 6380.600586, interst ratio 0.041213.
  232. NO[231]: sk = 239.510712, bk = 6141.089844, sk + bk = 6380.600586, interst ratio 0.037537.
  233. NO[232]: sk = 215.969864, bk = 6164.630859, sk + bk = 6380.600586, interst ratio 0.033848.
  234. NO[233]: sk = 192.338776, bk = 6188.261719, sk + bk = 6380.600586, interst ratio 0.030144.
  235. NO[234]: sk = 168.617111, bk = 6211.983398, sk + bk = 6380.600586, interst ratio 0.026427.
  236. NO[235]: sk = 144.804504, bk = 6235.795898, sk + bk = 6380.600586, interst ratio 0.022694.
  237. NO[236]: sk = 120.900620, bk = 6259.700195, sk + bk = 6380.600586, interst ratio 0.018948.
  238. NO[237]: sk = 96.905106, bk = 6283.695312, sk + bk = 6380.600586, interst ratio 0.015187.
  239. NO[238]: sk = 72.817604, bk = 6307.783203, sk + bk = 6380.600586, interst ratio 0.011412.
  240. NO[239]: sk = 48.637772, bk = 6331.962891, sk + bk = 6380.600586, interst ratio 0.007623.
  241. NO[240]: sk = 24.365248, bk = 6356.235352, sk + bk = 6380.600586, interst ratio 0.003819.

总利息额 

总利息最好算了，在等额本息情况下，每月的还款额都是固定的。所以：

总利息=每月还款额* 还款月数 - 总贷款本金额.

也就是：

\boldsymbol{Total_{intrest} = X\cdot n - M}

当然，实际场景中，年利率是浮动变化的，尤其是新的LPR基准利率施行后，每个月都会有一个新的LPR基准利率，但是无论利率如何变化，都是在新的利率的基础上调用上述公式，公式的形式是不会变化的。

计算利息总额，根据上面的公式，首先计算每月还款额X，贷款利率为4.6%

\\\boldsymbol{X=\frac{M\cdot \frac{R}{12 }\cdot (1+\frac{R}{12})^k}{(1+\frac{R}{12})^k-1}=M\cdot\frac{ \frac{R}{12 }\cdot (1+\frac{R}{12})^k}{(1+\frac{R}{12})^k-1}=1000000\cdot \frac{ \frac{0.046}{12 }\cdot (1+\frac{0.046}{12})^{240}}{(1+\frac{0.046}{12})^{240}-1}}

高次幂过于繁琐，这里编程实现：

得到每月还款额为6380.600586元。

所以总共利息为:

\boldsymbol{Total_{intrest} = X\cdot n - M =6380.600586\cdot 240 - 1000000 = 531344.14064 }

总支付利息与本金的比例为53.13%,也就是有相当于本金一半多的利息。

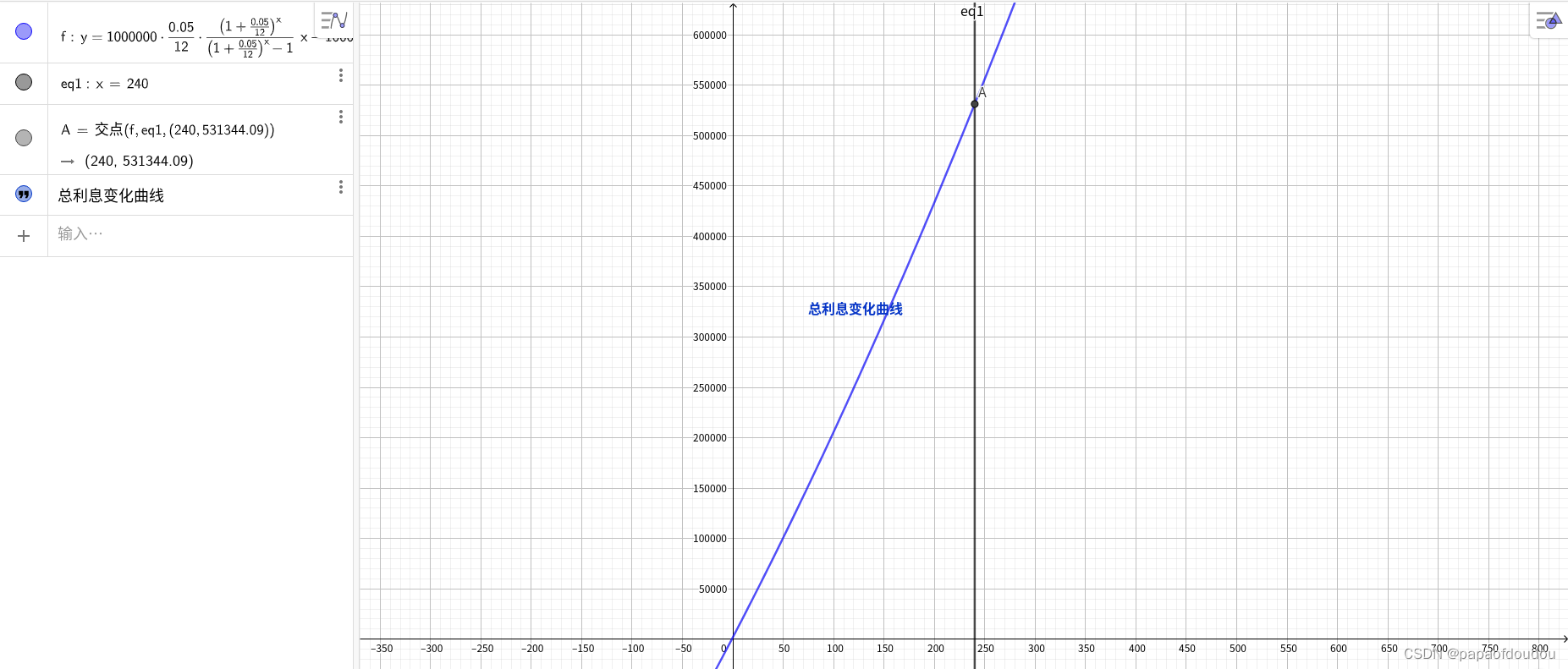
另外，通过公式

\boldsymbol{Total_{intrest} = X\cdot n - M =1000000\cdot \frac{ \frac{0.046}{12 }\cdot (1+\frac{0.046}{12})^{n}}{(1+\frac{0.046}{12})^{n}-1 }*n-1000000}

可以看到总的利息额和还款周期的关系，还款期越长，缴纳的利息越多。

等额本金还款方式：

等额本金的处理方式简单很多，还是以上面的条件为例，贷款总额M，按照每月固定本金还款，20年240个月，所以每月应还本金为：

\boldsymbol{B=\frac{M}{240}}

比如一个人公积金贷款36万元，贷款利率3.2%，贷款周期240个月，采用等额本金方式还款，每个月固定还款总额便为1500元本金，这样看余款清单，每个月都是整数：

360000/240=1500

假设经过K个月的还款，则下一个月的还款利息为:

\mathbf{S_{k+1}=(M-K\cdot B)\cdot \frac{R}{12}}

共计当月总还款额为:

\boldsymbol{Q_{k+1}=S_{k+1}+B=(M-K\cdot\frac{M}{240})\cdot \frac{R}{12}+\frac{M}{240}=M\cdot [\frac{(240-k)\cdot R+12}{240\cdot12}]}

等额本金还款方式支付的利息总和：

\boldsymbol{Interst =M\frac{R}{12} + (M-\frac{M}{240})\frac{R}{12}+ \cdots + (M-\frac{239M}{240})\frac{R}{12}=M\cdot \frac{R}{12}\cdot[1 + \frac{239}{240}+\cdots + \frac{1}{240}]}

\\\mathbf{=M\cdot \frac{R}{12}\cdot[\frac{240}{240} + \frac{239}{240}+\cdots + \frac{1}{240}]=M\cdot \frac{R}{12}\cdot 120.5}

其实通过上面的推导出的公式也可以看出，对于任意一个还款期限n月，其宗的利息为

\\\mathbf{M\cdot \frac{R}{12}\cdot[\frac{n}{n} + \frac{n-1}{n}+\cdots + \frac{1}{n}]=M\cdot \frac{R}{12}\cdot \frac{n+1}{2}}

从公式可以看出，利息总额和还款周期月数成正比。

M=1000000情况下，贷款年利率k为4.6%时，还款20年，共计利息为：1000000*0.046/12*120.5=461916.666667 元。与本金的比例为46.2%,利息量约占本金的不到一半。

对比之前等额本息的还款方式需要支付的利息数531344.14064

则，采用等额本金的还款方式后，可以节省利息为：

\boldsymbol{531344.14064-461916.666667=69427.473973}

也就是，固定本金大约可以节省7万元利息。既然可以节省这么多的利息，是不是说明固定本金要好于固定本息呢？不一定，原因有两点:

1.等额本息每个月还款一样，还款前期的压力不会太大，开始的月供要小于固定本金.

2.相对于固定本金，固定本息持有本金的时间更长（最后才开始大规模还本金),对于善于投资的，可能投资赚到的钱高于多支付的利息，借的越多越久，对自己越有利。

关于第二点，我们可以证明：

\boldsymbol{B_{k}= X-S_{k}=X(\frac{R}{12}+1)^{k-1}-M\cdot\frac{R}{12}\cdot(\frac{R}{12}+1)^{k-1}=(\frac{R}{12}+1)^{k-1}(X-M\cdot \frac{R}{12})}

第n期后，剩余本金为

\mathbf{Res=M-B_1-B_2-\cdots-B_{n}=M-(B_1+B_2+\cdots+B_{n})=M+(X-M\cdot \frac{R}{12})\cdot \frac{1-(1+\frac{R}{12})^n}{\frac{R}{12}}}

等额本金的剩余余额：

Res=1000000-4166.67\cdot n

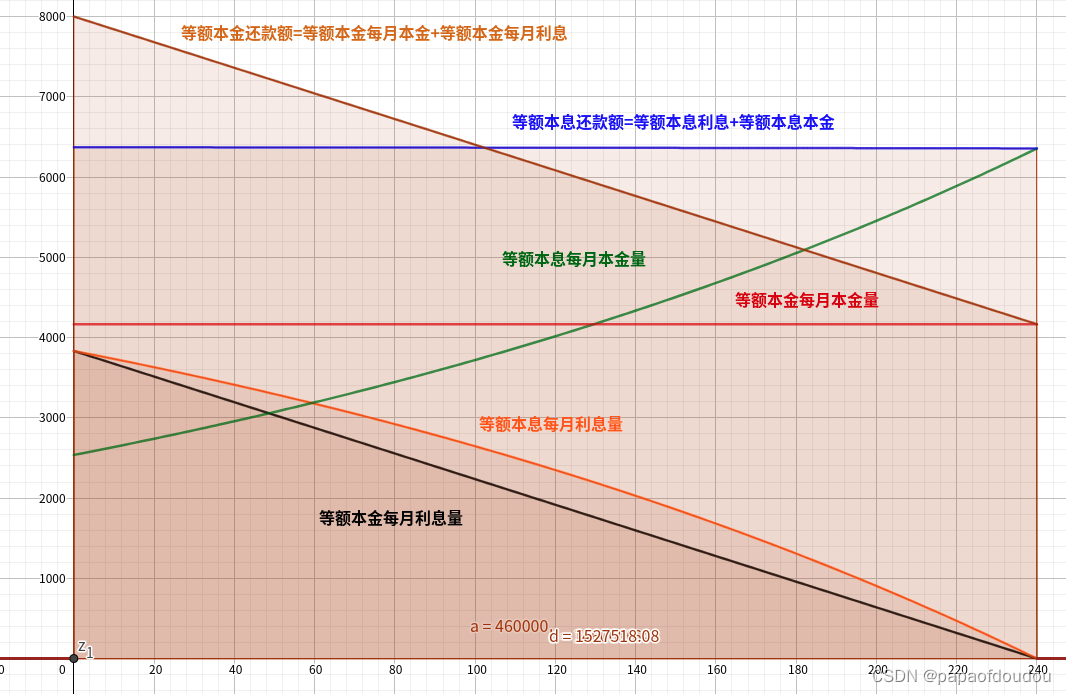
绘图如下，不用计算积分，肉眼可以明显看到等额本息曲线下与坐标轴围城的面积大于等额本金下的面积，这说明等额本息情况下，对银行贷款资金的占用能力更强（单位为元*月），对于善于理财投资高的手来说，可以将这部分资金转化为收益，如果收益大于多支付的利息，可以选择这种。

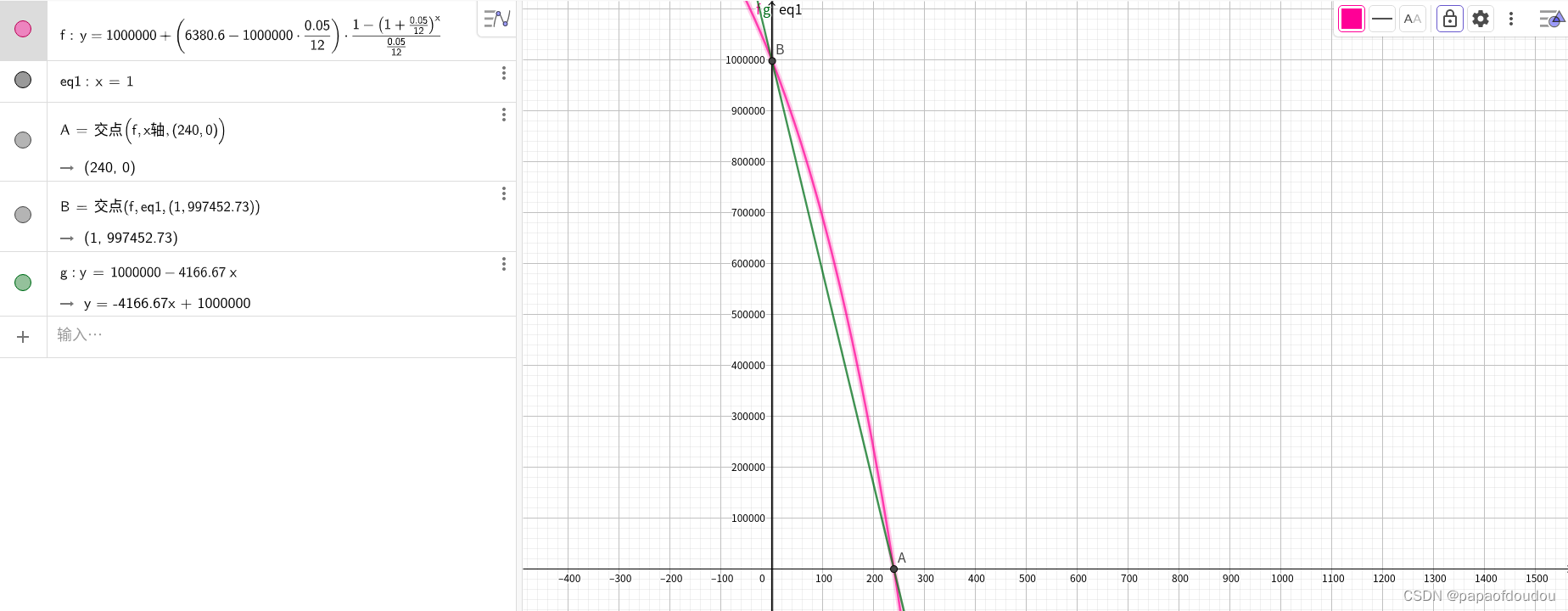
还有一个疑问，等额本息一开始还款本金额小于等额本金，从上图中可以看到很明显了，但是能否证明以下呢？

前面推导得知，等额本息每月还款本金额为：

\boldsymbol{B_{k}= X-S_{k}=X(\frac{R}{12}+1)^{k-1}-M\cdot\frac{R}{12}\cdot(\frac{R}{12}+1)^{k-1}=M\cdot\frac{ \frac{R}{12 }\cdot (1+\frac{R}{12})^{240}}{(1+\frac{R}{12})^{240}-1}\cdot (\frac{R}{12}+1)^{k-1}-M\cdot\frac{R}{12}\cdot(\frac{R}{12}+1)^{k-1}=[M\cdot\frac{R}{12}\cdot(\frac{R}{12}+1)^{k-1}]\cdot \frac{1}{(1+\frac{R}{12})^{240}-1}}

而等额本金每月偿还本金额为：

        \frac{M}{240}

要证明前者比后者大，还是作图吧：

从图中可以看出，等额本息的还款方式每月还款本金是低开高走，本金额度逐月增加，但是等额本金下，每月还款本金额度不变，并且两条曲线一定存在交点，表示在在整个还款周期，一定存在一个时间点，在这个时间点下，等额本金和等额本息下，当前还款本金额度是相同的。在下面的例子中，这个时间点发生在第130个还款月。

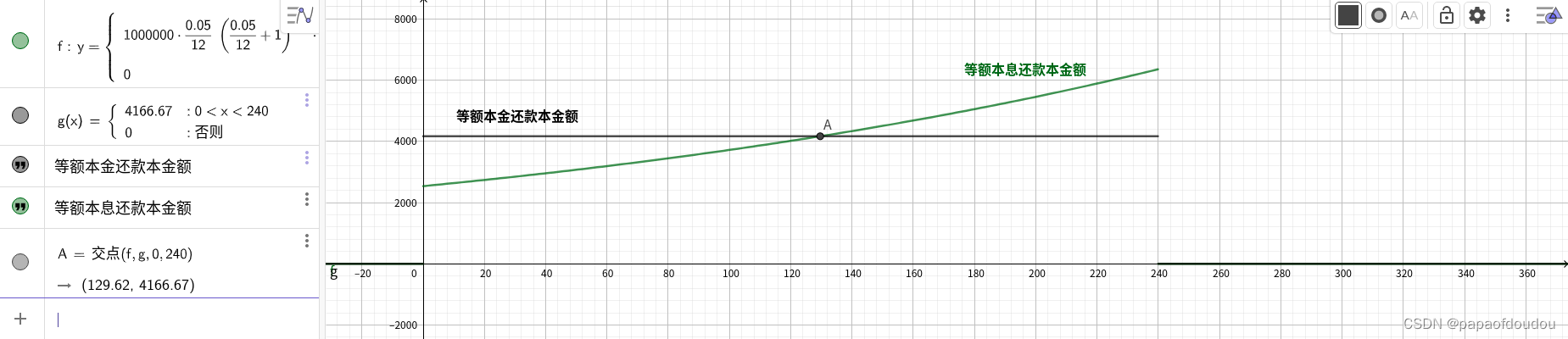
第129-130个月附近本金情况，可以看到还款本金额在这里发生了交叉，具体可看文章后续表格。

等额本金下本息平衡点：

韭菜疯涨的年代，每月的利息甚至超过了当月的本金额，但是由于利息在这个还款周期中是一个单调下降的曲线，所以在整个还款期内，一定有一个时间点，每月利息开始少于本金。

每期还款额：

M\cdot [\frac{(240-k)\cdot R+12}{240\cdot12}]

每期还款本金：

\frac{M}{K}

列出不等式：

M\cdot [\frac{(240-k)\cdot R+12}{240\cdot12}] -\frac{M}{K} < \frac{M}{K}=> \frac{(240-k)\cdot R+12}{240\cdot12}<\frac{2}{K}

所以：

2\cdot12 > (K-k)\cdot R+12=>k>K-\frac{12}{R}

可以看到，边界月是总的还款月和年利息的函数，当总还款周期为K月，年利率为R时，从第

K-\frac{12}{R}

月开始，每月的本金开始大于利息。和贷款总额无关。

所以，如果你对每月还款的利息比本金还要多心理上过不去，在无法选择降低年利率的情况下，只能选择缩短还款周期。比如，以年利率3.6，30年等额本金还款说明，其k为360-12/0.036=27.从第27个月开始，本金大约利息，编程验证，得到的结果也是27：

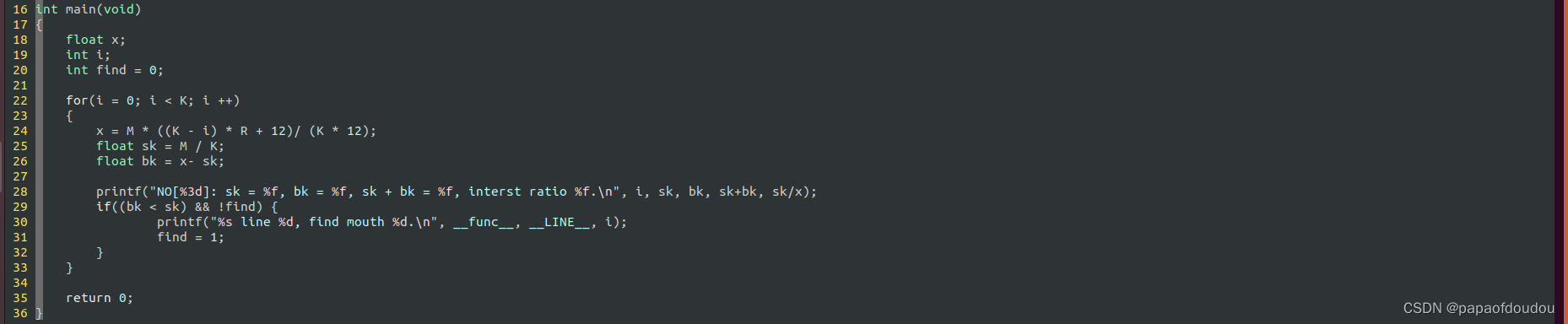
如果选择贷款年年限小于12/0.036=333，约等于26年，则还款周期内不会出现利息高于本金的月份.作为韭菜，心理上会不会舒服一些？

每月利息的变化趋势：

等额本息：

\boldsymbol{S_{k+1}=S_k-B_k\cdot\frac{R}{12}=M\cdot \frac{R}{12}\cdot (\frac{R}{12}+1)^{k}-X(\frac{R}{12}+1)^{k}+X}

等额本金：

\mathbf{S_{k+1}=(M-K\cdot B)\cdot \frac{R}{12}}

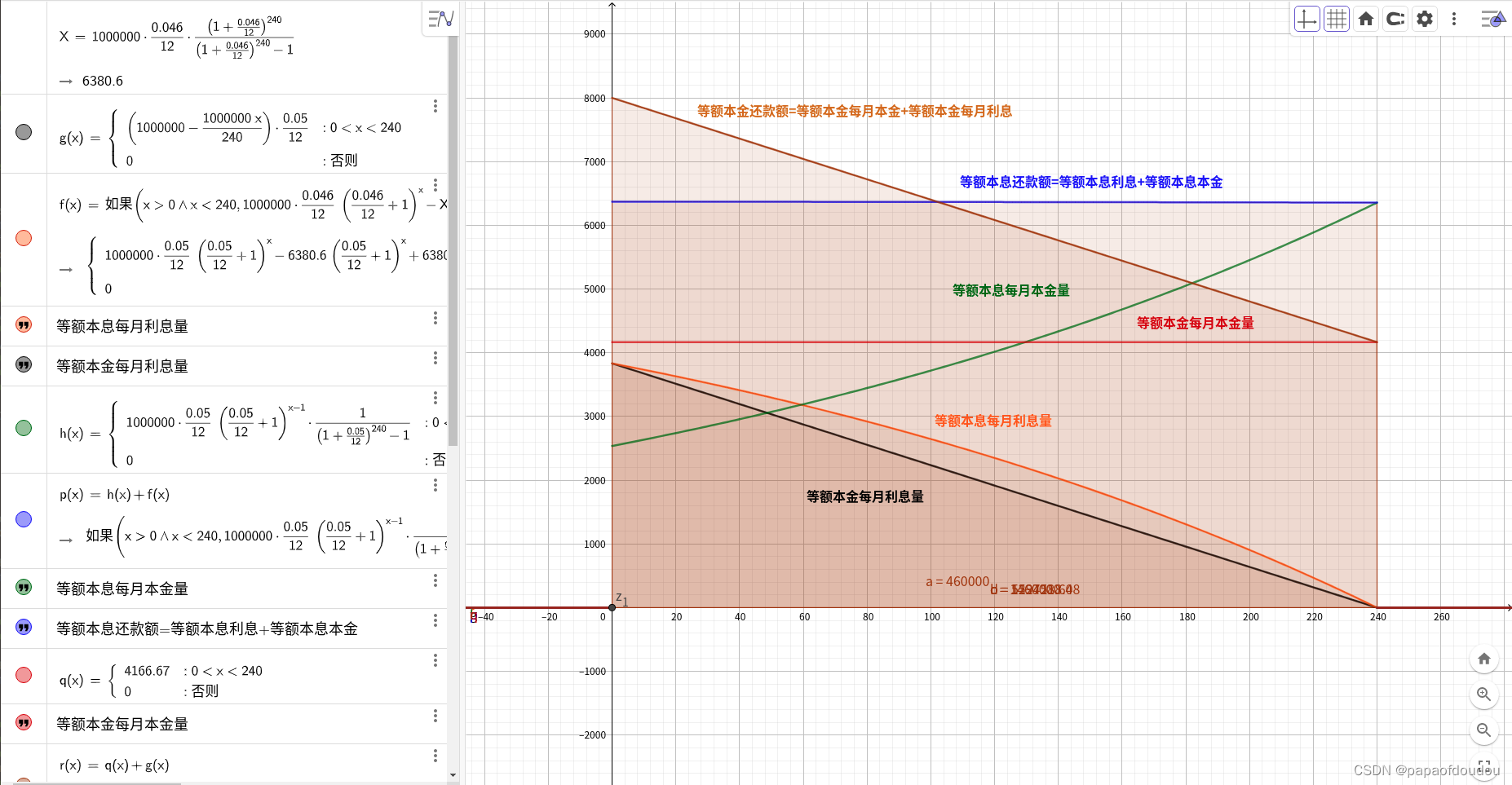
绘图如下，可以看到，等额本息利息曲线和坐标轴围城的面积大于等额本金，所以等额本息的总利息高于等额本金。

综合分析如下图，注意等额本息的利息曲线和本金曲线恰好互补为一条斜率为0的直线，等额本息嘛，而等额本金则是一条一次曲线,斜率为\frac{M}{240}\cdot\frac{R}{12}，也就是每月还款减少额，它等于每期本金产生的利息。

如下图，等额本金的利息曲线和本金曲线都是一次直线，所以等额本金的月还款额也是直线。而等额本息的利息曲线和本金曲线都是曲线（高次），但是叠加再一起的效果是一条一次的水平直线，每月还款额相同。

根据计算公式，制定还款计划

有了以上推导出来的公式，我们就可以分别制定两种方式下的还款计划表了,如下：

等额本金还款方式等额本息还款方式
贷款期次偿还本息偿还利息偿还本金剩余本金偿还本息偿还利息偿还本金剩余本金
18,000.003,833.334,166.67995,833.336,380.603,833.332,547.27997,452.73
27,984.033,817.364,166.67991,666.676,380.603,823.572,557.03994,895.70
37,968.063,801.394,166.67987,500.006,380.603,813.772,566.83992,328.87
47,952.083,785.424,166.67983,333.336,380.603,803.932,576.67989,752.19
57,936.113,769.444,166.67979,166.676,380.603,794.052,586.55987,165.64
67,920.143,753.474,166.67975,000.006,380.603,784.132,596.47984,569.18
77,904.173,737.504,166.67970,833.336,380.603,774.182,606.42981,962.76
87,888.193,721.534,166.67966,666.676,380.603,764.192,616.41979,346.35
97,872.223,705.564,166.67962,500.006,380.603,754.162,626.44976,719.91
107,856.253,689.584,166.67958,333.336,380.603,744.092,636.51974,083.40
117,840.283,673.614,166.67954,166.676,380.603,733.992,646.61971,436.79
127,824.313,657.644,166.67950,000.006,380.603,723.842,656.76968,780.03
137,808.333,641.674,166.67945,833.336,380.603,713.662,666.94966,113.09
147,792.363,625.694,166.67941,666.676,380.603,703.432,677.17963,435.92
157,776.393,609.724,166.67937,500.006,380.603,693.172,687.43960,748.49
167,760.423,593.754,166.67933,333.336,380.603,682.872,697.73958,050.76
177,744.443,577.784,166.67929,166.676,380.603,672.532,708.07955,342.69
187,728.473,561.814,166.67925,000.006,380.603,662.152,718.45952,624.23
197,712.503,545.834,166.67920,833.336,380.603,651.732,728.87949,895.36
207,696.533,529.864,166.67916,666.676,380.603,641.272,739.33947,156.02
217,680.563,513.894,166.67912,500.006,380.603,630.762,749.84944,406.19
227,664.583,497.924,166.67908,333.336,380.603,620.222,760.38941,645.81
237,648.613,481.944,166.67904,166.676,380.603,609.642,770.96938,874.85
247,632.643,465.974,166.67900,000.006,380.603,599.022,781.58936,093.27
257,616.673,450.004,166.67895,833.336,380.603,588.362,792.24933,301.03
267,600.693,434.034,166.67891,666.676,380.603,577.652,802.95930,498.09
277,584.723,418.064,166.67887,500.006,380.603,566.912,813.69927,684.39
287,568.753,402.084,166.67883,333.336,380.603,556.122,824.48924,859.92
297,552.783,386.114,166.67879,166.676,380.603,545.302,835.30922,024.61
307,536.813,370.144,166.67875,000.006,380.603,534.432,846.17919,178.44
317,520.833,354.174,166.67870,833.336,380.603,523.522,857.08916,321.36
327,504.863,338.194,166.67866,666.676,380.603,512.572,868.04913,453.32
337,488.893,322.224,166.67862,500.006,380.603,501.572,879.03910,574.29
347,472.923,306.254,166.67858,333.336,380.603,490.532,890.07907,684.23
357,456.943,290.284,166.67854,166.676,380.603,479.462,901.14904,783.08
367,440.973,274.314,166.67850,000.006,380.603,468.342,912.27901,870.82
377,425.003,258.334,166.67845,833.336,380.603,457.172,923.43898,947.39
387,409.033,242.364,166.67841,666.676,380.603,445.962,934.64896,012.75
397,393.063,226.394,166.67837,500.006,380.603,434.722,945.88893,066.87
407,377.083,210.424,166.67833,333.336,380.603,423.422,957.18890,109.69
417,361.113,194.444,166.67829,166.676,380.603,412.092,968.51887,141.18
427,345.143,178.474,166.67825,000.006,380.603,400.712,979.89884,161.29
437,329.173,162.504,166.67820,833.336,380.603,389.282,991.32881,169.97
447,313.193,146.534,166.67816,666.676,380.603,377.823,002.78878,167.19
457,297.223,130.564,166.67812,500.006,380.603,366.313,014.29875,152.90
467,281.253,114.584,166.67808,333.336,380.603,354.753,025.85872,127.05
477,265.283,098.614,166.67804,166.676,380.603,343.153,037.45869,089.60
487,249.313,082.644,166.67800,000.006,380.603,331.513,049.09866,040.51
497,233.333,066.674,166.67795,833.336,380.603,319.823,060.78862,979.73
507,217.363,050.694,166.67791,666.676,380.603,308.093,072.51859,907.22
517,201.393,034.724,166.67787,500.006,380.603,296.313,084.29856,822.93
527,185.423,018.754,166.67783,333.336,380.603,284.493,096.11853,726.82
537,169.443,002.784,166.67779,166.676,380.603,272.623,107.98850,618.84
547,153.472,986.814,166.67775,000.006,380.603,260.713,119.89847,498.94
557,137.502,970.834,166.67770,833.336,380.603,248.753,131.85844,367.09
567,121.532,954.864,166.67766,666.676,380.603,236.743,143.86841,223.23
577,105.562,938.894,166.67762,500.006,380.603,224.693,155.91838,067.32
587,089.582,922.924,166.67758,333.336,380.603,212.593,168.01834,899.31
597,073.612,906.944,166.67754,166.676,380.603,200.453,180.15831,719.16
607,057.642,890.974,166.67750,000.006,380.603,188.263,192.34828,526.81
617,041.672,875.004,166.67745,833.336,380.603,176.023,204.58825,322.23
627,025.692,859.034,166.67741,666.676,380.603,163.743,216.87822,105.37
637,009.722,843.064,166.67737,500.006,380.603,151.403,229.20818,876.17
646,993.752,827.084,166.67733,333.336,380.603,139.033,241.58815,634.59
656,977.782,811.114,166.67729,166.676,380.603,126.603,254.00812,380.59
666,961.812,795.144,166.67725,000.006,380.603,114.133,266.47809,114.12
676,945.832,779.174,166.67720,833.336,380.603,101.603,279.00805,835.12
686,929.862,763.194,166.67716,666.676,380.603,089.033,291.57802,543.56
696,913.892,747.224,166.67712,500.006,380.603,076.423,304.18799,239.37
706,897.922,731.254,166.67708,333.336,380.603,063.753,316.85795,922.52
716,881.942,715.284,166.67704,166.676,380.603,051.043,329.56792,592.96
726,865.972,699.314,166.67700,000.006,380.603,038.273,342.33789,250.63
736,850.002,683.334,166.67695,833.336,380.603,025.463,355.14785,895.49
746,834.032,667.364,166.67691,666.676,380.603,012.603,368.00782,527.49
756,818.062,651.394,166.67687,500.006,380.602,999.693,380.91779,146.58
766,802.082,635.424,166.67683,333.336,380.602,986.733,393.87775,752.71
776,786.112,619.444,166.67679,166.676,380.602,973.723,406.88772,345.83
786,770.142,603.474,166.67675,000.006,380.602,960.663,419.94768,925.89
796,754.172,587.504,166.67670,833.336,380.602,947.553,433.05765,492.83
806,738.192,571.534,166.67666,666.676,380.602,934.393,446.21762,046.62
816,722.222,555.564,166.67662,500.006,380.602,921.183,459.42758,587.20
826,706.252,539.584,166.67658,333.336,380.602,907.923,472.68755,114.52
836,690.282,523.614,166.67654,166.676,380.602,894.613,485.99751,628.52
846,674.312,507.644,166.67650,000.006,380.602,881.243,499.36748,129.17
856,658.332,491.674,166.67645,833.336,380.602,867.833,512.77744,616.39
866,642.362,475.694,166.67641,666.676,380.602,854.363,526.24741,090.16
876,626.392,459.724,166.67637,500.006,380.602,840.853,539.75737,550.40
886,610.422,443.754,166.67633,333.336,380.602,827.283,553.32733,997.08
896,594.442,427.784,166.67629,166.676,380.602,813.663,566.94730,430.13
906,578.472,411.814,166.67625,000.006,380.602,799.983,580.62726,849.52
916,562.502,395.834,166.67620,833.336,380.602,786.263,594.34723,255.17
926,546.532,379.864,166.67616,666.676,380.602,772.483,608.12719,647.05
936,530.562,363.894,166.67612,500.006,380.602,758.653,621.95716,025.10
946,514.582,347.924,166.67608,333.336,380.602,744.763,635.84712,389.26
956,498.612,331.944,166.67604,166.676,380.602,730.833,649.77708,739.48
966,482.642,315.974,166.67600,000.006,380.602,716.833,663.77705,075.72
976,466.672,300.004,166.67595,833.336,380.602,702.793,677.81701,397.91
986,450.692,284.034,166.67591,666.676,380.602,688.693,691.91697,706.00
996,434.722,268.064,166.67587,500.006,380.602,674.543,706.06693,999.94
1006,418.752,252.084,166.67583,333.336,380.602,660.333,720.27690,279.67
1016,402.782,236.114,166.67579,166.676,380.602,646.073,734.53686,545.14
1026,386.812,220.144,166.67575,000.006,380.602,631.763,748.84682,796.30
1036,370.832,204.174,166.67570,833.336,380.602,617.393,763.21679,033.08
1046,354.862,188.194,166.67566,666.676,380.602,602.963,777.64675,255.44
1056,338.892,172.224,166.67562,500.006,380.602,588.483,792.12671,463.32
1066,322.922,156.254,166.67558,333.336,380.602,573.943,806.66667,656.67
1076,306.942,140.284,166.67554,166.676,380.602,559.353,821.25663,835.42
1086,290.972,124.314,166.67550,000.006,380.602,544.703,835.90659,999.52
1096,275.002,108.334,166.67545,833.336,380.602,530.003,850.60656,148.92
1106,259.032,092.364,166.67541,666.676,380.602,515.243,865.36652,283.55
1116,243.062,076.394,166.67537,500.006,380.602,500.423,880.18648,403.37
1126,227.082,060.424,166.67533,333.336,380.602,485.553,895.05644,508.32
1136,211.112,044.444,166.67529,166.676,380.602,470.623,909.99640,598.33
1146,195.142,028.474,166.67525,000.006,380.602,455.633,924.97636,673.36
1156,179.172,012.504,166.67520,833.336,380.602,440.583,940.02632,733.34
1166,163.191,996.534,166.67516,666.676,380.602,425.483,955.12628,778.22
1176,147.221,980.564,166.67512,500.006,380.602,410.323,970.28624,807.93
1186,131.251,964.584,166.67508,333.336,380.602,395.103,985.50620,822.43
1196,115.281,948.614,166.67504,166.676,380.602,379.824,000.78616,821.65
1206,099.311,932.644,166.67500,000.006,380.602,364.484,016.12612,805.53
1216,083.331,916.674,166.67495,833.336,380.602,349.094,031.51608,774.02
1226,067.361,900.694,166.67491,666.676,380.602,333.634,046.97604,727.05
1236,051.391,884.724,166.67487,500.006,380.602,318.124,062.48600,664.57
1246,035.421,868.754,166.67483,333.336,380.602,302.554,078.05596,586.52
1256,019.441,852.784,166.67479,166.676,380.602,286.914,093.69592,492.84
1266,003.471,836.814,166.67475,000.006,380.602,271.224,109.38588,383.46
1275,987.501,820.834,166.67470,833.336,380.602,255.474,125.13584,258.33
1285,971.531,804.864,166.67466,666.676,380.602,239.664,140.94580,117.38
1295,955.561,788.894,166.67462,500.006,380.602,223.784,156.82575,960.57
1305,939.581,772.924,166.67458,333.336,380.602,207.854,172.75571,787.81
1315,923.611,756.944,166.67454,166.676,380.602,191.854,188.75567,599.07
1325,907.641,740.974,166.67450,000.006,380.602,175.804,204.80563,394.26
1335,891.671,725.004,166.67445,833.336,380.602,159.684,220.92559,173.34
1345,875.691,709.034,166.67441,666.676,380.602,143.504,237.10554,936.24
1355,859.721,693.064,166.67437,500.006,380.602,127.264,253.34550,682.89
1365,843.751,677.084,166.67433,333.336,380.602,110.954,269.65546,413.24
1375,827.781,661.114,166.67429,166.676,380.602,094.584,286.02542,127.23
1385,811.811,645.144,166.67425,000.006,380.602,078.154,302.45537,824.78
1395,795.831,629.174,166.67420,833.336,380.602,061.664,318.94533,505.84
1405,779.861,613.194,166.67416,666.676,380.602,045.114,335.49529,170.35
1415,763.891,597.224,166.67412,500.006,380.602,028.494,352.11524,818.24
1425,747.921,581.254,166.67408,333.336,380.602,011.804,368.80520,449.44
1435,731.941,565.284,166.67404,166.676,380.601,995.064,385.54516,063.89
1445,715.971,549.314,166.67400,000.006,380.601,978.244,402.36511,661.54
1455,700.001,533.334,166.67395,833.336,380.601,961.374,419.23507,242.31
1465,684.031,517.364,166.67391,666.676,380.601,944.434,436.17502,806.14
1475,668.061,501.394,166.67387,500.006,380.601,927.424,453.18498,352.96
1485,652.081,485.424,166.67383,333.336,380.601,910.354,470.25493,882.71
1495,636.111,469.444,166.67379,166.676,380.601,893.224,487.38489,395.33
1505,620.141,453.474,166.67375,000.006,380.601,876.024,504.58484,890.74
1515,604.171,437.504,166.67370,833.336,380.601,858.754,521.85480,368.89
1525,588.191,421.534,166.67366,666.676,380.601,841.414,539.19475,829.70
1535,572.221,405.564,166.67362,500.006,380.601,824.014,556.59471,273.12
1545,556.251,389.584,166.67358,333.336,380.601,806.554,574.05466,699.06
1555,540.281,373.614,166.67354,166.676,380.601,789.014,591.59462,107.48
1565,524.311,357.644,166.67350,000.006,380.601,771.414,609.19457,498.29
1575,508.331,341.674,166.67345,833.336,380.601,753.744,626.86452,871.43
1585,492.361,325.694,166.67341,666.676,380.601,736.014,644.59448,226.84
1595,476.391,309.724,166.67337,500.006,380.601,718.204,662.40443,564.44
1605,460.421,293.754,166.67333,333.336,380.601,700.334,680.27438,884.17
1615,444.441,277.784,166.67329,166.676,380.601,682.394,698.21434,185.96
1625,428.471,261.814,166.67325,000.006,380.601,664.384,716.22429,469.74
1635,412.501,245.834,166.67320,833.336,380.601,646.304,734.30424,735.44
1645,396.531,229.864,166.67316,666.676,380.601,628.154,752.45419,982.99
1655,380.561,213.894,166.67312,500.006,380.601,609.934,770.67415,212.33
1665,364.581,197.924,166.67308,333.336,380.601,591.654,788.95410,423.37
1675,348.611,181.944,166.67304,166.676,380.601,573.294,807.31405,616.06
1685,332.641,165.974,166.67300,000.006,380.601,554.864,825.74400,790.32
1695,316.671,150.004,166.67295,833.336,380.601,536.364,844.24395,946.09
1705,300.691,134.034,166.67291,666.676,380.601,517.794,862.81391,083.28
1715,284.721,118.064,166.67287,500.006,380.601,499.154,881.45386,201.83
1725,268.751,102.084,166.67283,333.336,380.601,480.444,900.16381,301.67
1735,252.781,086.114,166.67279,166.676,380.601,461.664,918.94376,382.73
1745,236.811,070.144,166.67275,000.006,380.601,442.804,937.80371,444.93
1755,220.831,054.174,166.67270,833.336,380.601,423.874,956.73366,488.20
1765,204.861,038.194,166.67266,666.676,380.601,404.874,975.73361,512.47
1775,188.891,022.224,166.67262,500.006,380.601,385.804,994.80356,517.67
1785,172.921,006.254,166.67258,333.336,380.601,366.655,013.95351,503.72
1795,156.94990.284,166.67254,166.676,380.601,347.435,033.17346,470.55
1805,140.97974.314,166.67250,000.006,380.601,328.145,052.46341,418.09
1815,125.00958.334,166.67245,833.336,380.601,308.775,071.83336,346.25
1825,109.03942.364,166.67241,666.676,380.601,289.335,091.27331,254.98
1835,093.06926.394,166.67237,500.006,380.601,269.815,110.79326,144.19
1845,077.08910.424,166.67233,333.336,380.601,250.225,130.38321,013.81
1855,061.11894.444,166.67229,166.676,380.601,230.555,150.05315,863.76
1865,045.14878.474,166.67225,000.006,380.601,210.815,169.79310,693.97
1875,029.17862.504,166.67220,833.336,380.601,190.995,189.61305,504.37
1885,013.19846.534,166.67216,666.676,380.601,171.105,209.50300,294.87
1894,997.22830.564,166.67212,500.006,380.601,151.135,229.47295,065.40
1904,981.25814.584,166.67208,333.336,380.601,131.085,249.52289,815.88
1914,965.28798.614,166.67204,166.676,380.601,110.965,269.64284,546.24
1924,949.31782.644,166.67200,000.006,380.601,090.765,289.84279,256.40
1934,933.33766.674,166.67195,833.336,380.601,070.485,310.12273,946.28
1944,917.36750.694,166.67191,666.676,380.601,050.135,330.47268,615.81
1954,901.39734.724,166.67187,500.006,380.601,029.695,350.91263,264.90
1964,885.42718.754,166.67183,333.336,380.601,009.185,371.42257,893.49
1974,869.44702.784,166.67179,166.676,380.60988.595,392.01252,501.48
1984,853.47686.814,166.67175,000.006,380.60967.925,412.68247,088.80
1994,837.50670.834,166.67170,833.336,380.60947.175,433.43241,655.37
2004,821.53654.864,166.67166,666.676,380.60926.355,454.25236,201.12
2014,805.56638.894,166.67162,500.006,380.60905.445,475.16230,725.96
2024,789.58622.924,166.67158,333.336,380.60884.455,496.15225,229.80
2034,773.61606.944,166.67154,166.676,380.60863.385,517.22219,712.59
2044,757.64590.974,166.67150,000.006,380.60842.235,538.37214,174.22
2054,741.67575.004,166.67145,833.336,380.60821.005,559.60208,614.62
2064,725.69559.034,166.67141,666.676,380.60799.695,580.91203,033.71
2074,709.72543.064,166.67137,500.006,380.60778.305,602.30197,431.40
2084,693.75527.084,166.67133,333.336,380.60756.825,623.78191,807.62
2094,677.78511.114,166.67129,166.676,380.60735.265,645.34186,162.28
2104,661.81495.144,166.67125,000.006,380.60713.625,666.98180,495.31
2114,645.83479.174,166.67120,833.336,380.60691.905,688.70174,806.60
2124,629.86463.194,166.67116,666.676,380.60670.095,710.51169,096.10
2134,613.89447.224,166.67112,500.006,380.60648.205,732.40163,363.70
2144,597.92431.254,166.67108,333.336,380.60626.235,754.37157,609.32
2154,581.94415.284,166.67104,166.676,380.60604.175,776.43151,832.89
2164,565.97399.314,166.67100,000.006,380.60582.035,798.57146,034.32
2174,550.00383.334,166.6795,833.336,380.60559.805,820.80140,213.52
2184,534.03367.364,166.6791,666.676,380.60537.495,843.12134,370.40
2194,518.06351.394,166.6787,500.006,380.60515.095,865.51128,504.89
2204,502.08335.424,166.6783,333.336,380.60492.605,888.00122,616.89
2214,486.11319.444,166.6779,166.676,380.60470.035,910.57116,706.32
2224,470.14303.474,166.6775,000.006,380.60447.375,933.23110,773.09
2234,454.17287.504,166.6770,833.336,380.60424.635,955.97104,817.12
2244,438.19271.534,166.6766,666.676,380.60401.805,978.8098,838.32
2254,422.22255.564,166.6762,500.006,380.60378.886,001.7292,836.60
2264,406.25239.584,166.6758,333.336,380.60355.876,024.7386,811.88
2274,390.28223.614,166.6754,166.676,380.60332.786,047.8280,764.05
2284,374.31207.644,166.6750,000.006,380.60309.606,071.0074,693.05
2294,358.33191.674,166.6745,833.336,380.60286.326,094.2868,598.77
2304,342.36175.694,166.6741,666.676,380.60262.966,117.6462,481.13
2314,326.39159.724,166.6737,500.006,380.60239.516,141.0956,340.04
2324,310.42143.754,166.6733,333.336,380.60215.976,164.6350,175.41
2334,294.44127.784,166.6729,166.676,380.60192.346,188.2643,987.15
2344,278.47111.814,166.6725,000.006,380.60168.626,211.9837,775.17
2354,262.5095.834,166.6720,833.336,380.60144.806,235.8031,539.37
2364,246.5379.864,166.6716,666.676,380.60120.906,259.7025,279.67
2374,230.5663.894,166.6712,500.006,380.6096.916,283.6918,995.98
2384,214.5847.924,166.678,333.336,380.6072.826,307.7812,688.20
2394,198.6131.944,166.674,166.676,380.6048.646,331.966,356.23
2404,182.6415.974,166.670.006,380.6024.376,356.230.00
总和1461916.67461916.661000000.8/1531344531344.12999999.94/

分析

无论等额本金还是等额本息，它们第一个月的利息数是相同的，都是3833.33元，原因很显然，首月来讲，两种方式对记息的影响还没有体现，都是总贷款额的利息。但是由于等额本金每月还款的本金多余等额本息，所以等额本金第一个月的还款额高于等额本息，表现为8000和6380.6，但是随着时间推移，等额本金每月还款额度会减少。

其实，如果你选择的是等额本息的话，可以根据第一个月的利息计算出等额本金下第一个月应还款总额，计算方法是：

3833.33+1000000/240 = 8000

等额本金每月具体会少多少呢？根据前面计算的等差公式

M\cdot \frac{R}{12}\cdot \frac{1}{240}= 15.9722222222

也就是每个月少不到16块钱，对比一下实际数据即可确认这个规律, 并且，等额本金还款方式下，最后一个月的还款利息恰好就是一个本金还款额所产生的利息。

也就是，等额本金每月还款额的减少量符合如下公式：

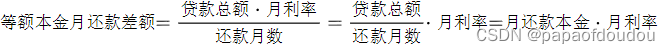
这个公式很直观，理解起来也不难，因为固定本金还款，每月还款本金数量是一定的，相应减少的利息就是上个月本金产生的了。利息会陪伴你到还清本金的那一刻，等额本金最后一个还款月的利息就是这个差额，编程计算等额本金每月还款情况以及额度比例：

  1. #include <stdio.h>
  2. #include <stdlib.h>
  3. #include <math.h>
  4.  
  5. #if 1
  6. #define M 1000000
  7. #define K 240
  8. #define R 0.046f
  9. #else
  10. #define M 1500000
  11. #define K 360
  12. #define R 0.036f
  13. #endif
  14.  
  15. int main(void)
  16. {
  17.     float x;
  18.     int i;
  19.  
  20.     for(i = 0; i < K; i ++)
  21.     {
  22.         x = M * ((K - i) * R + 12)/ (K * 12);
  23.         float sk = M / K;
  24.         float bk = x- sk;
  25.  
  26.         printf("NO[%3d]: sk = %f, bk = %f, sk + bk = %f, interst ratio %f.\n", i, sk, bk, sk+bk, sk/x);
  27.     }
  28.  
  29.     return 0;
  30. }

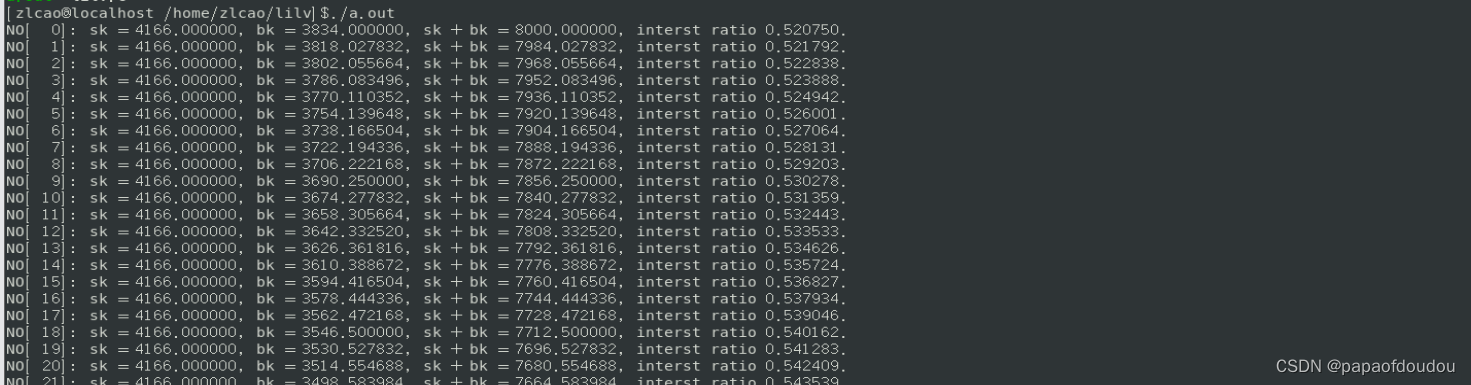
可以结合自身情况验证一下计算公式的正确性，等额本金每月还款额是一个等差数列：

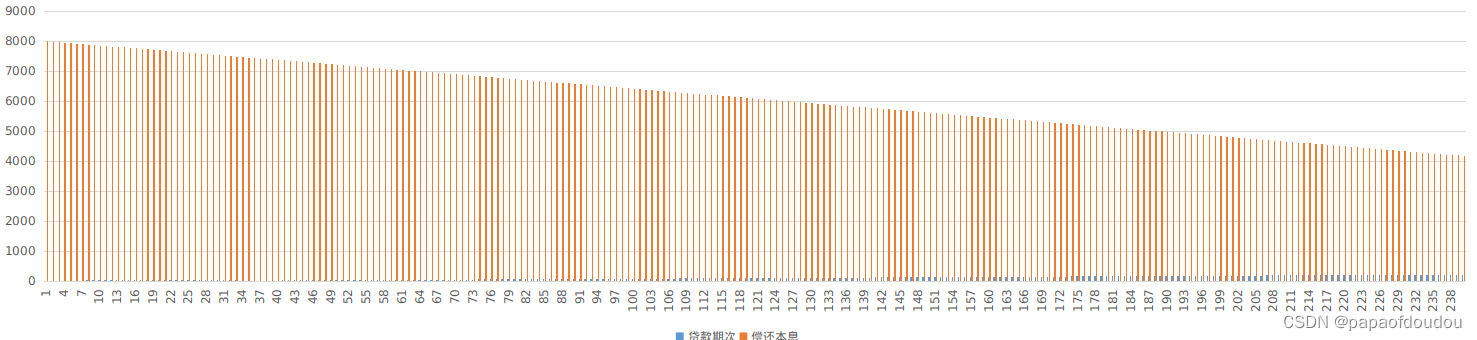
等额本金每月利息偿还情况，也是等差数列

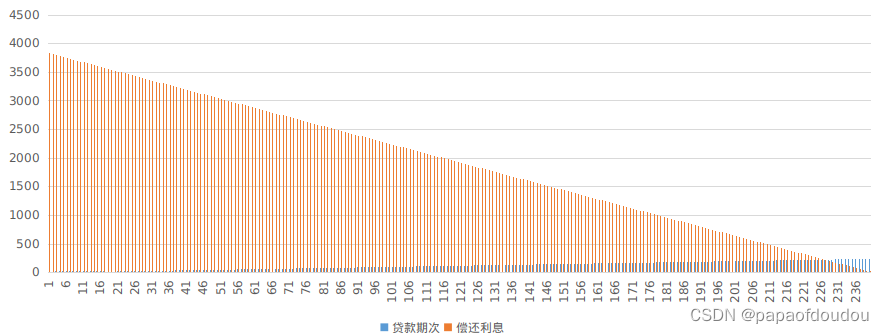
等额本金还款每月剩余本金情况，依然是等差数列。

等额本息每月还利息情况，可以看到这是一个曲线

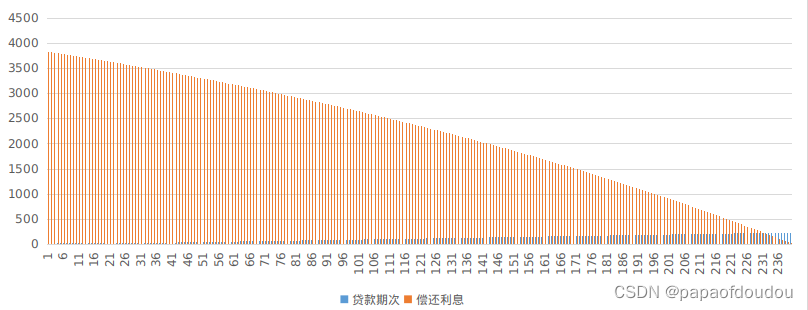
等额本息每月偿还本金情况，可以看到，等额本息先还利息，在还本金，越往后，本金占比越大。

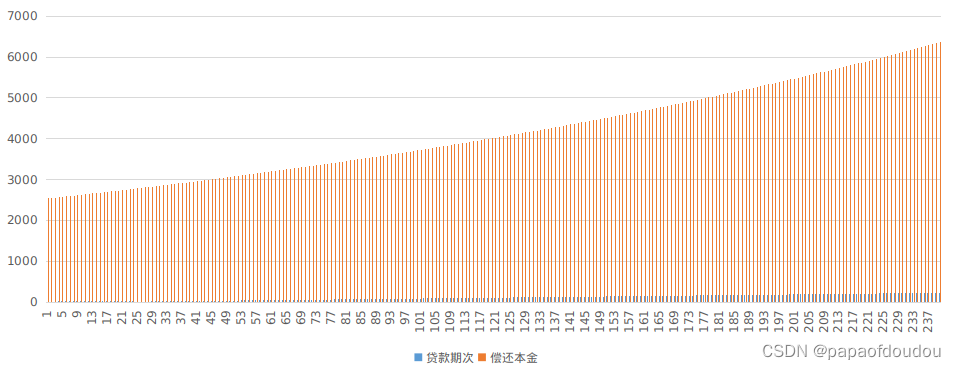
由于等额本息每月还款数额相同，所以上面两幅图是互补的。

等额本息剩余本金情况，可以看到，一开始本金下降速度比较慢，因为大部分的钱都用来还利息了。

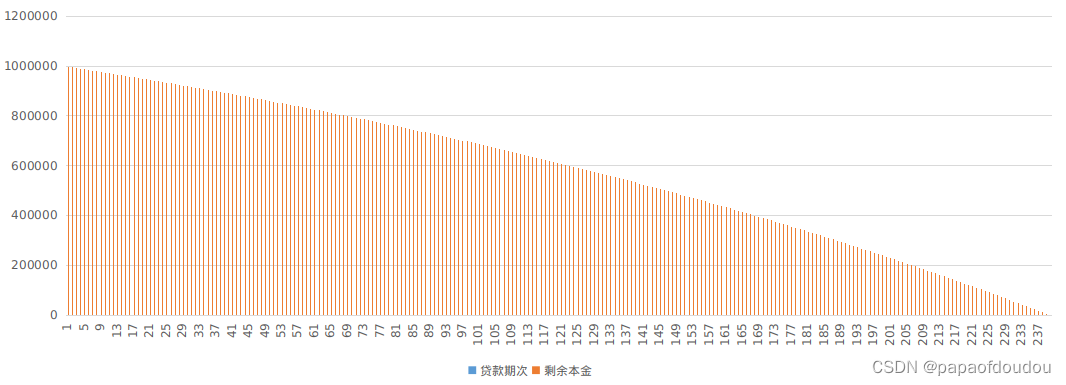以上就是对两种还款方式的简要分析，究竟选择那种方式要看本人情况而定.

单利和复利

利息有两种存在形式，分别是单利和复利， 它们的区别如下：

单利：是指按照固定的本金计算利息即本金固定。

复利：是指在计算第二次本金的时候里面要包括第一次产生的利息，所以又叫利滚利。

以本金x,月利率r,月数n为例，它们的账户金额变化情况为：

单利为：

y=x\cdot (1+r\cdot n)

复利为：

y=x\cdot (1+r)^n

前者是一次函数，后者是底数大于1的指数函数，所以一定是复利的增长更快一些，两者的比例变化为：

y=\frac{(1+r)^n}{1+n\cdot r}

以月利率0.3为例，变化规律为：

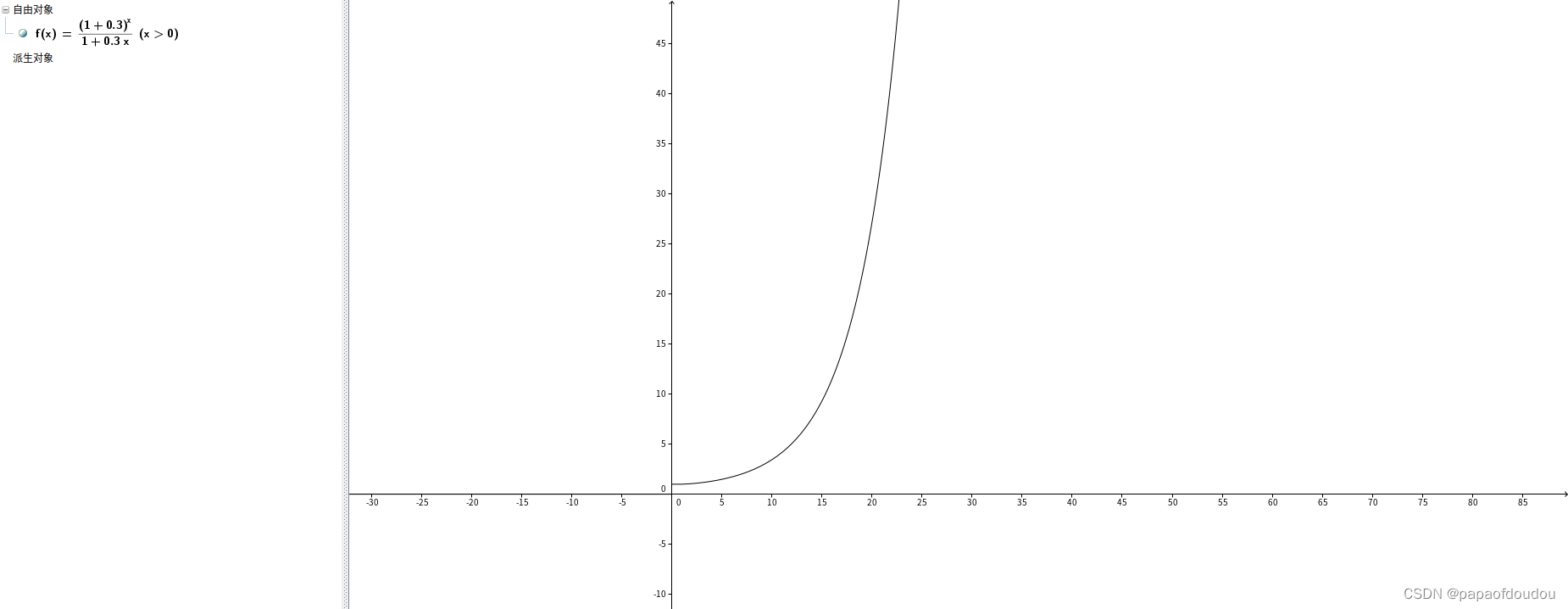
从图形上看，复利的优势到后期越明显。

复利是对未来的盈利增长统计，而计算历史过去的增长率叫做“复合增长率”，它的计算就是对上面的式子求逆：

假设某年的利润是x,n年后，利润增长到y,则年复合增长率为：

r=(\frac{y}{x})^\frac{1}{n} -1

累积本金和利息额

对于等额本息的情况，每月偿还本金额为：

X=M\cdot\frac{ \frac{R}{12 }\cdot (1+\frac{R}{12})^k}{(1+\frac{R}{12})^k-1}

S_k = M\cdot \frac{R}{12}\cdot (\frac{R}{12}+1)^{k}-X(\frac{R}{12}+1)^{k}+X

B_{k}= X-S_{k}=X(\frac{R}{12}+1)^{k}-M\cdot\frac{R}{12}\cdot(\frac{R}{12}+1)^{k}=(X-M\cdot\frac{R}{12})(\frac{R}{12}+1)^k

则累积K月后，总的本金还款额为：

T_n=B_0+B_1+\cdots+B_n=(X-M\cdot\frac{R}{12})\frac{(1+\frac{R}{12})^n-1}{\frac{R}{12}}

偿还利息的进度为：

I_n= S_0+S_n+\cdots+S_n = nX-T_n

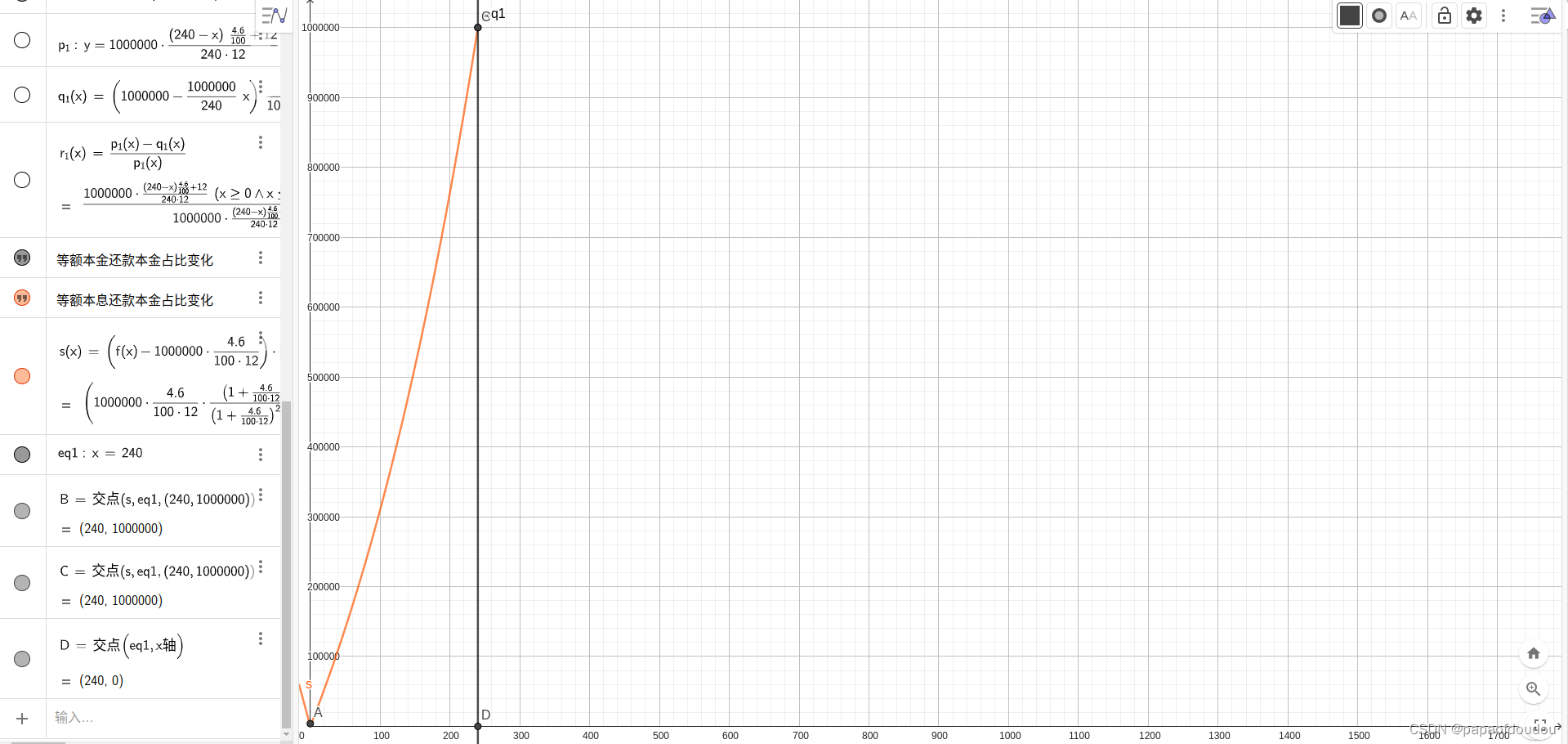
所以，还款总利息额和还款总本金额随着还款期的变化趋势如下图示，看图说明，那前例来说，采用等额本息的还款模式，当你还完最后一笔本金的时候，已经还了大约53万的利息了。

我们有时会看到一些自媒体作者讲述自己购房的血泪经历，控诉银行贷款的高利率，比如说到还款三年有一半多的钱是在还利息，情况真的是这样么?  当我们绘制出总的利息额和总的还款额随时间变化的曲线的时候，很不幸地发现这些描述都是真实的。下图所示，可以看到还款第一个月，利息是本金的1.51倍，直到第115个月，还款利息都是大于本金的，本金占比在还款周期的后半程才后来居上，不过这已经占整个还款期的一半时间了，所以，如果你计划提前还款，建议你越早越好，晚了就没有多大意义了。

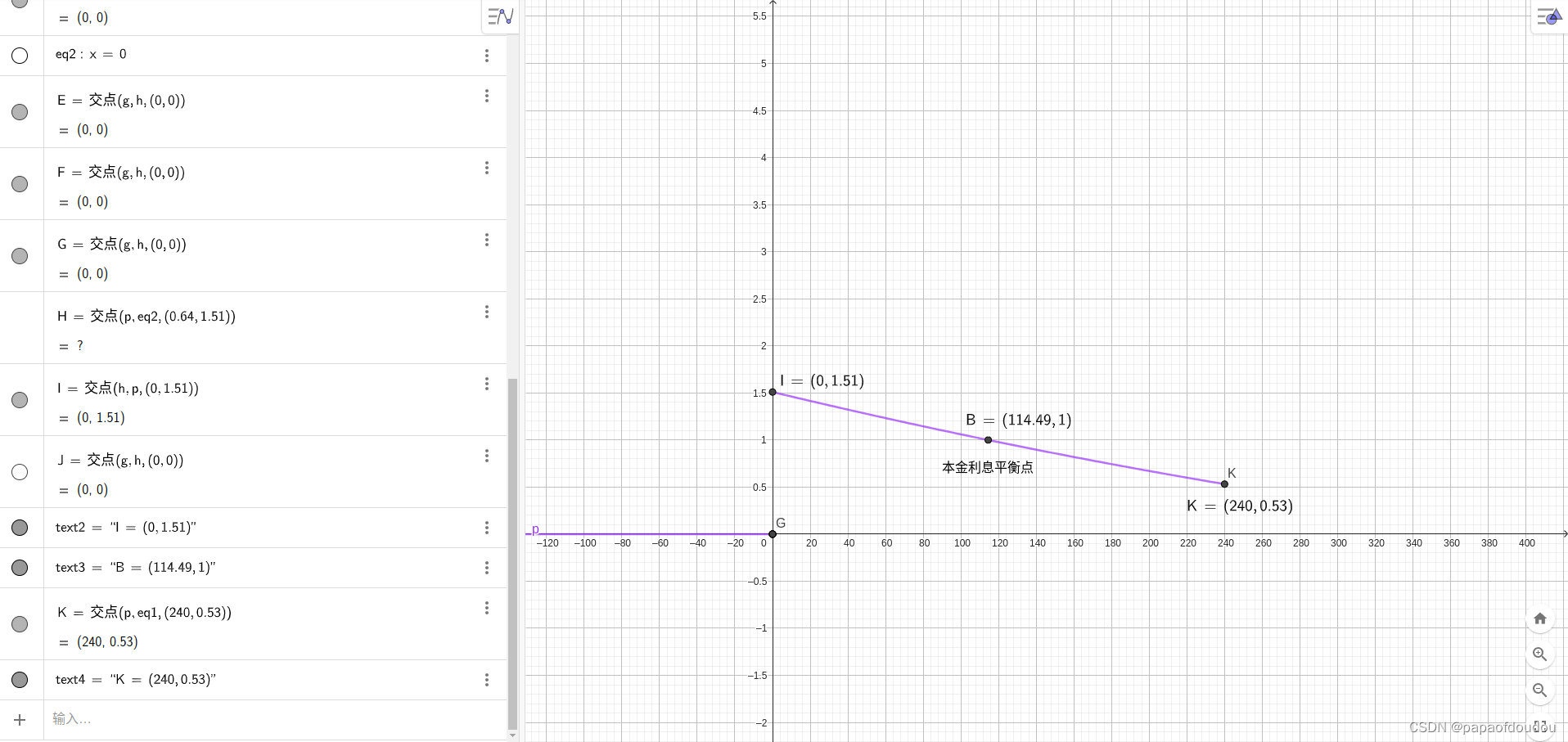
等额本金累计利息和本金还款额变化：

B=\frac{M}{240}

S_{k}=(M-K\cdot B)\cdot \frac{R}{12}=(M-K\cdot \frac{M}{240})\cdot \frac{R}{12}

总计前N个月还款本息额为：

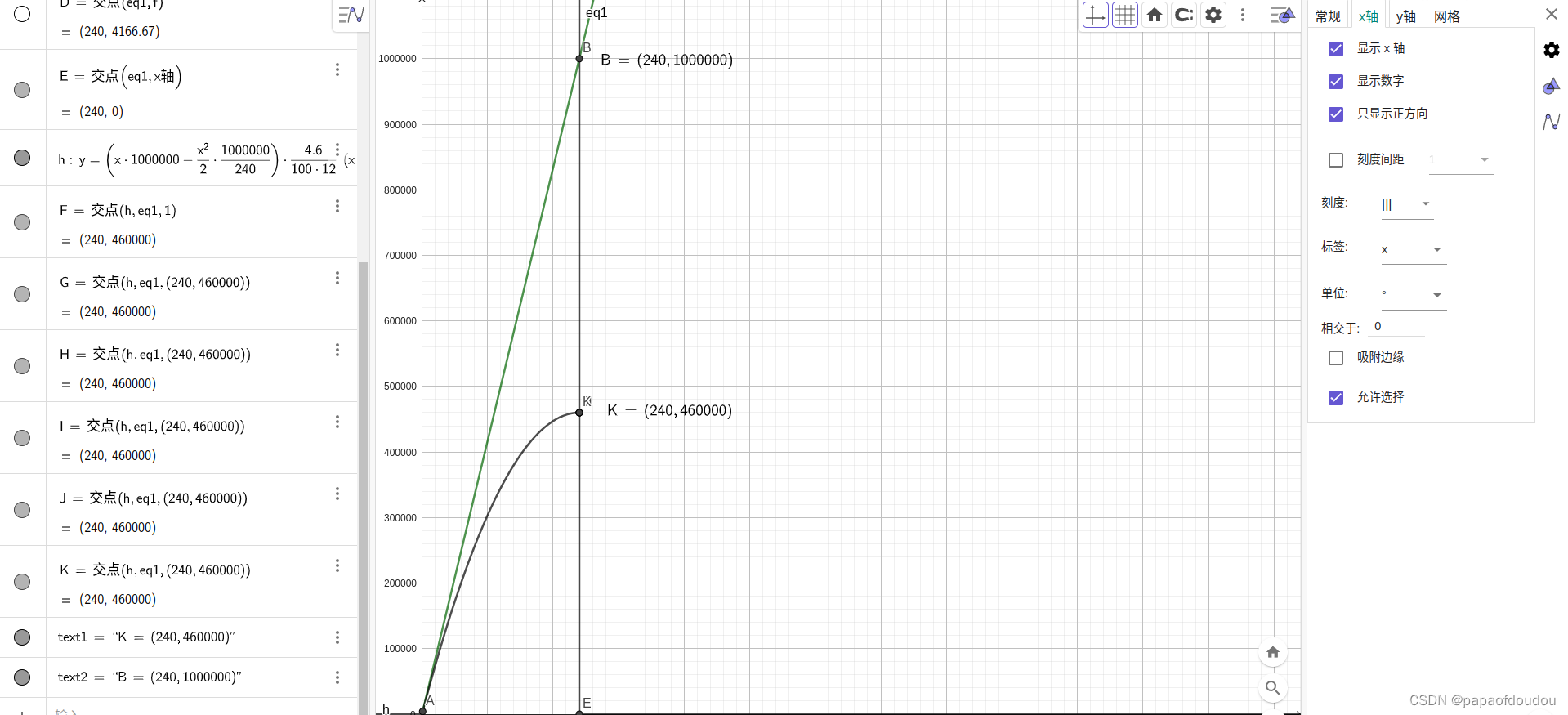
I_n = s_0+s_1+\cdots+s_n =(nM-\frac{n^2}{2})\cdot \frac{R}{12}

可以看到，等额本金还款情况下，本金还款总额是一条一次曲线，而累计利息还款总额是一条二次曲线，在240月达到最高点，也就是46万的时候偿还完所有的本息。相比另一种方式的利息总额531344元，节省了7万多。

提前还款

对于当前投资回报率低的情况，未来的通胀预期强烈，很多人没有较好的投资渠道抵抗房贷的利息，所以与其将钱放在手上逐渐贬值，还不如提前还贷来的划算。也有一部分人是不喜欢欠钱的感觉，即便是债权人是银行也不可以。但是无论贷款属于上述哪种情况，都是从你提前还款的下个月的剩余本金中减去你的提前还款额，在此基础上再重新利用上面的公式计算剩余每个月的还款计划，不再分析。

总结：

等额本金的优劣分析：

1.还款额总和少于等额本息，主要原因是等额本金总利息少.

2.还款初期压力较大，还款末期压力较小。

如下图，两种方式利息的每月占比情况：

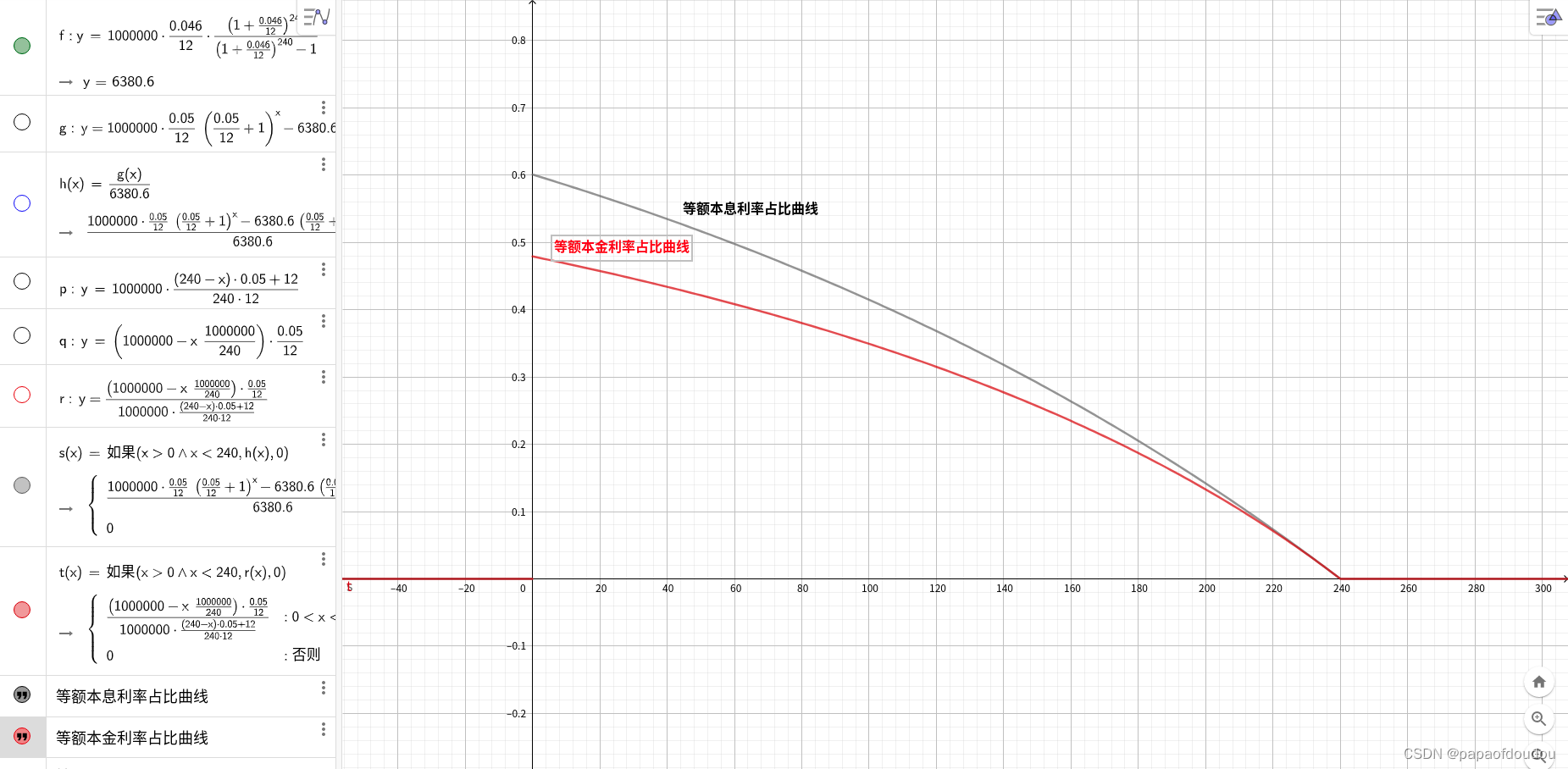
等额本息的优劣分析：

1.还款额总和大于等额本金，主要原因是等额本息情况下，还款前期利息比重大，末期才会体现出本金的比重.

2.每个还款期还款额度固定，便于提前安排家庭开支。

3.占用银行本金的能力强，对于善于理财投资的人来说，如果能够抵抗住多支付的利息，是个不错的选择。

4.如下图中所示，整个还款周期内，每个月利息所占还款金额的占比，等额本息都要比等额本金多。

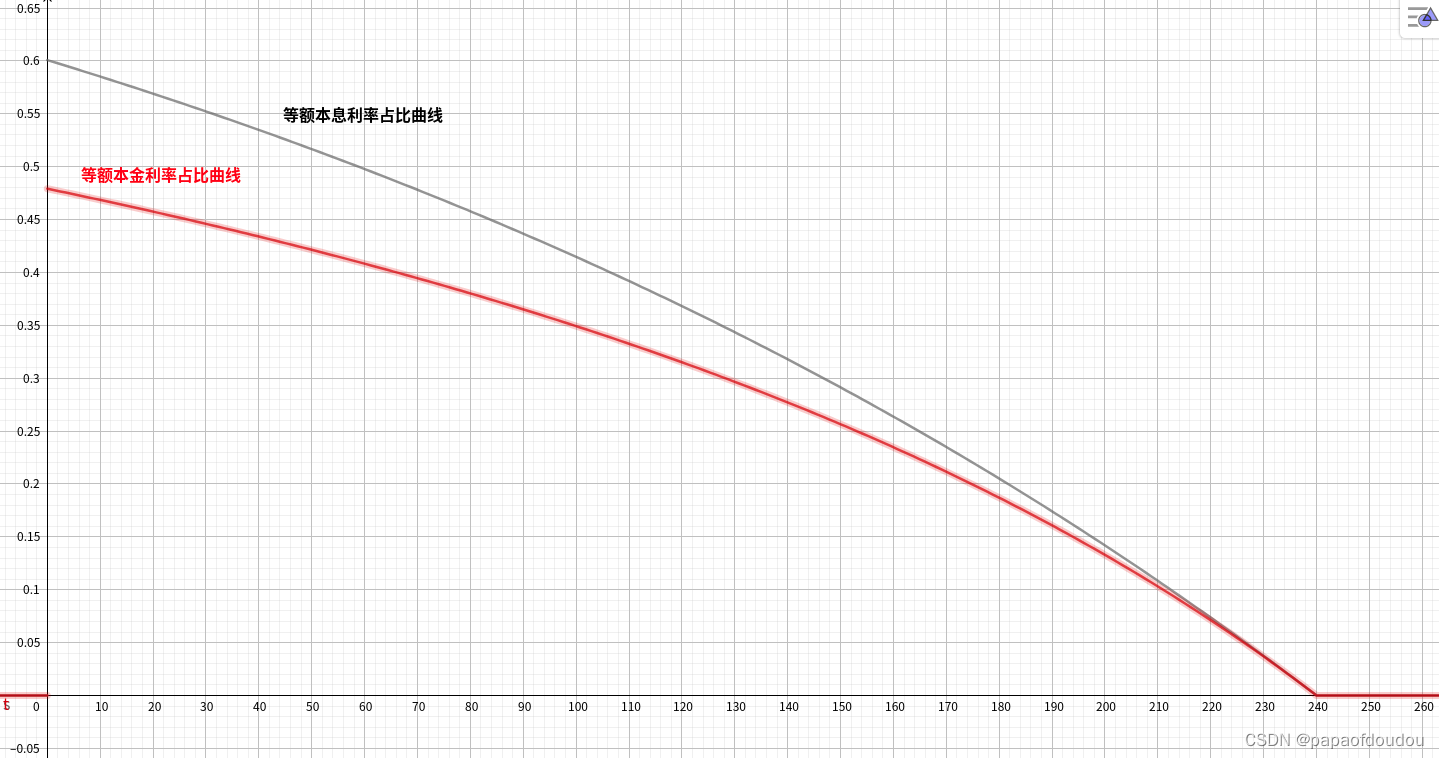
本金占比变化，可以看到，固定本金即便还款达到94期的时间点，本金占比也仅仅只有总还款额的2/3,大家如果有贷款的话，可以和你的实际情况做个对比，和理论计算得到的曲线基上是对的上的，印度的剥削制度才是赤裸裸的。

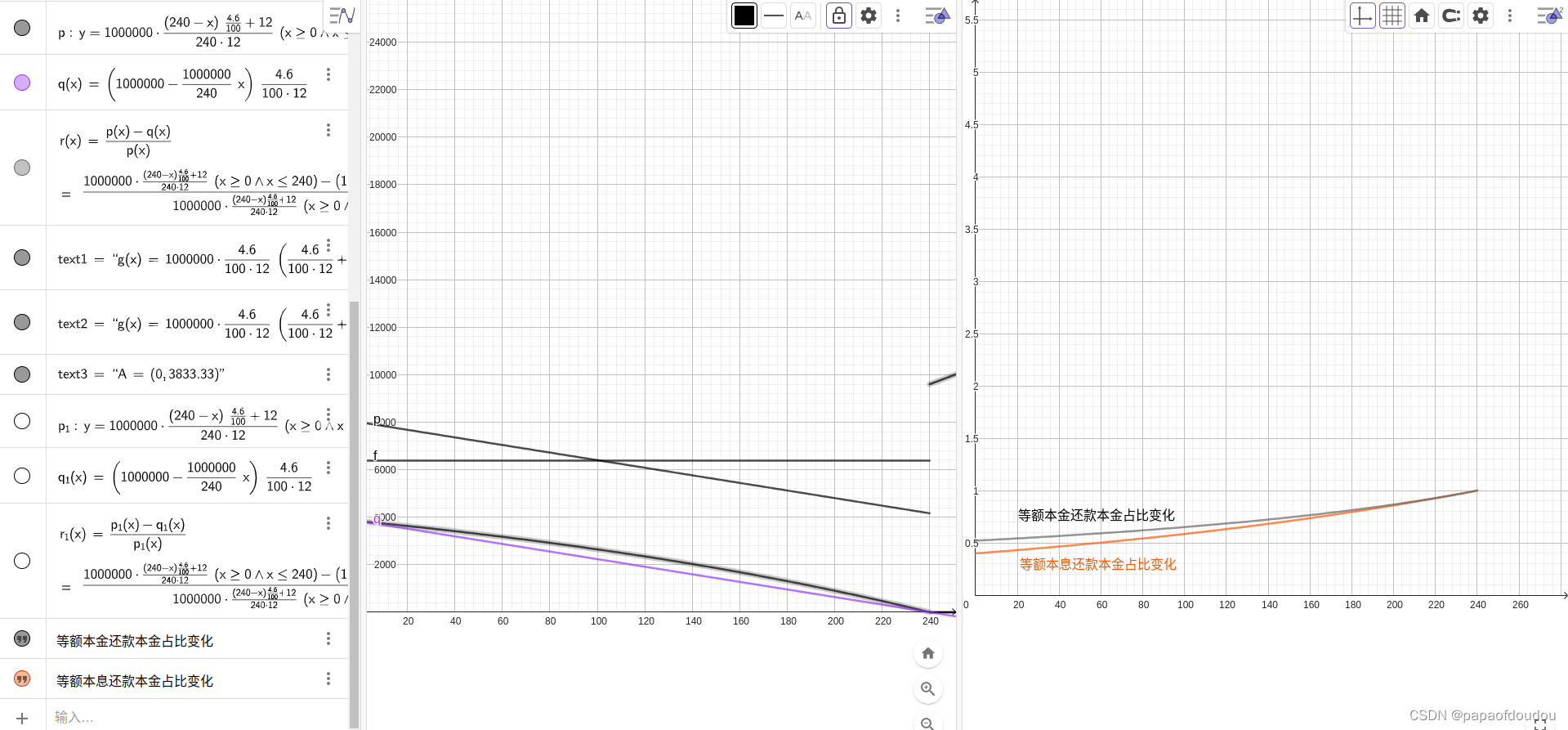
两种方式都遵守的规则：还款周期越长，缴纳利息越多.

和利息的关系

利息是由本金产生的，本金的变化率正比于利息的变化率，根据上面对两类还款方式的公式可以得到，等额本金情况下每月的利息是利率的一次函数，所以逐月利息构成一个等差数列逐渐减少，而等额本金下，由于每个月还款本金数量是不均匀的，所以每个月的利息数量和利率本身的关系比较复杂，利息按非线性规律变化。采用等额本金还款方式下，利息变化的影响直接而明显。

比如，当前珠海采用公积金贷款的利率是3.2，而商业贷款的利率是4.2贷款每降低一个点，按等额本金还款，你每月的还款压力就会少对应的比例，感受直接。

首月还款利息

银行从放款那一天开始计算利息，购房借贷人可以自由选择每月的还款日，但是由于银行的放贷日和购房者确定的还款日可能不是同一天，所以首月的利息可能会和公式中按整月计算出的利息有所出入，所以造成首月还款额度和公式计算出来的并不一样。尽管如此，首月还款日的不对齐并不影响之后每月的还款额度，从第二个月开始，每个月的还款金额和公式计算得到的结果是完全一致的。

比如说，银行15日放贷，而你确定的还款日是这个月16日开始，那么首月还款总金额就包括当月的本金加上1天的利息，就会比公式计算出来的首月还款额少。但是如果你确定的还款从下个月16日开始，则首月还款本金不变，利息则为一天的利息再加上一个完整月的利息了。这样，首月还款额就会更多。

但是无论如何，首月承担了所有之后，从第二个还款月开始，还款额度和公式计算得到的就完全一致了。

初始本金占比：

无论等额本金还是等额本息，第一个月的利息额都是总贷款额产生的，但是由于等额本金情况下还款本金额度大，所以利息占比的起点相对较低，之后逐渐减少。

等额本金初始的利息占比：

\frac{M\cdot \frac{R}{12}}{M\cdot \frac{R}{12} + \frac{M}{K}}=\frac{NR}{NR+1}=\frac{20\times 0.046}{20\times 0.046+1} = 0.479167.

等额本息初始利息占比：0.600779

题外话，我不太会同情那些高杠杆买房，拖家带口突然失业或者生病或者出意外，生活很拮据甚至走上绝路的人，完全没有危机意识，动不动贷款二三十年，几百万，动不动生二胎甚至三胎，谁能给你保证未来你一定有稳定收入呢？而且不稳定的概率还不小，即使贷款利率很高，他们认为用明天发生通货膨胀的钱来偿还今天用于购买房子，汽车的贷款是正确的做法，但是谁告诉你未来一定是通胀呢？成年人不考虑可能出现的不稳定因素，是自己的原因，因为你改变不了社会，只能自己控制风险。

LPR利率和基点

个人贷款利率由LPR基础利率+基点共同决定，个人贷款应用的LPR基础利率一年一调， 签贷款合同的时候，可以选择贷款日调或者每年一月一日调整。这样的话，贷款利率就可以随行就市，随着市场变化，尤其是当前下行的趋势下，基点是负的，并且LPR逐年下调，选择一个合适的点上车就非常重要了。

虽然基点也是调控手段，但是对于个人来说，合同签订后，基点就固定了，就是你签合同时候的市场基点。但是你仍然可以享受LPR下调带来的好处。LPR基础利率是普惠大众的，而基点则精准定位，都是调控手段，只不过一个是粗调，一个是细调。

其它参考

利用计算图计算公积金余额_papaofdoudou的博客-CSDN博客

房产证改为不动产权证是哪一年_法师兄

结束

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/从前慢现在也慢/article/detail/250818
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号