【SVM时间序列预测】粒子群算法优化支持向量机PSO-SVM时间序列预测【含Matlab源码 259期】_svm预测时间序列

⛄一、粒子群算法优化SVM预测简介

1 支持向量机方法
支持向量机的理论基础是结构风险最小化原则和VC维理论, 它是一种新型的机器学习方法, 并不是单纯地考虑经验风险, 还考虑了置信风险, 相比于传统的统计方法, 具有更强的推广能力, 能较好地解决非线性、高维度、局部极小等问题。SVM是在低维空间寻找最优分类面存在困难, 就将输入空间通过内积函数的变换映射到高维空间, 使得高维空间变得线性可分, 从而寻找到最优分类面。

在支持向量机方法中, 把线性可分推广到非线性可分, 引进适当的变换, 将原本在低维空间的训练点映射到高维Hilbert空间, 然后在高维空间中寻找一个超维平面, 使得这些样本点在高维空间中变得线性可分。在这个转化过程中, 最关键的就是找到这个非线性变换映射函数。Vapnik提出了核函数的方法, 该方法通过找到一个函数K (·, ·) , 使得K (xi, yj) =φ (xi) ·φ (xj) , 从而避免了高维的点积运算, 这样我们不需要知道映射函数φ (x) 的具体形式。

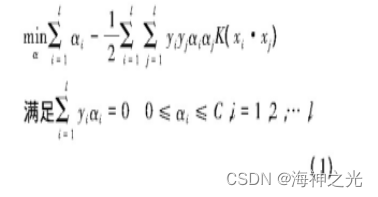
相应的决策函数为

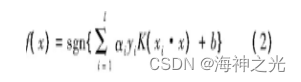
在实际问题中, 比较常见的是非线性问题, 而核函数的正确选取是解决非线性函数的关键。常见的核函数主要有3类, 分别是多项式核函数、高斯核函数和神经网络核函数。其中, 高斯核函数是效果最好的核函数, 这是因为它所对应的Hilbert空间的维数是无穷, 而有限训练样本在该Hil