自注意力机制（Self-Attention）_自注意力层

 注意：本文引用自专业人工智能社区Venus AI

更多AI知识请参考原站（【http://www.aideeplearning.cn】）

Transformer模型中最关键部分就是自注意力（Self-Attention）机制，正如 Transformer 的论文的标题是“Attention Is All You Need”！以文本问题为例来讲解这个机制。在处理文本问题时，自注意力机制会告诉模型：在处理句子中的每个单词时，特别关注某些重要的单词，并或多或少地忽略其它单词。简单来说，就是给句子中不同单词分配不同的权重。这是符合常理的，因为一句话中的每个单词重要程度是不一样的，从语法角度说，主谓宾语比其它句子成分更重要，self-attention机制就是模型尝试学习句子成分重要程度的方法。

self-attention可以通过学习句子成分重要程度更好的理解语言的上下文，而上下文对于语言模型来说是至关重要的。例如，看一下机器人第二定律：

机器人第二定律机器人必须服从人类发出的命令，除非这些命令与第一定律相冲突。

当模型处理这句话时，它必须能够知道：

• 它指的是机器人
• 这种命令指的是法律的前半部分，即“人类发出的命令”
• 第一定律指的是整个第一定律

如果不结合它们所指的上下文，就无法理解或处理这些单词。这就是自注意力的作用。它加深了模型对相关和关联词的理解，这些词在处理某个词（将其通过神经网络传递）之前解释了该词的上下文。它通过为片段中每个单词的相关程度分配分数，并将它们的向量表示相加来实现这一点。

例如，顶部块中的自注意力层在处理“it”一词时正在关注“a robots”。它将传递给神经网络的向量是三个单词中每个单词的向量乘以它们的权重分数的总和（这里忽略了那些权重分数低的不重要的单词）。

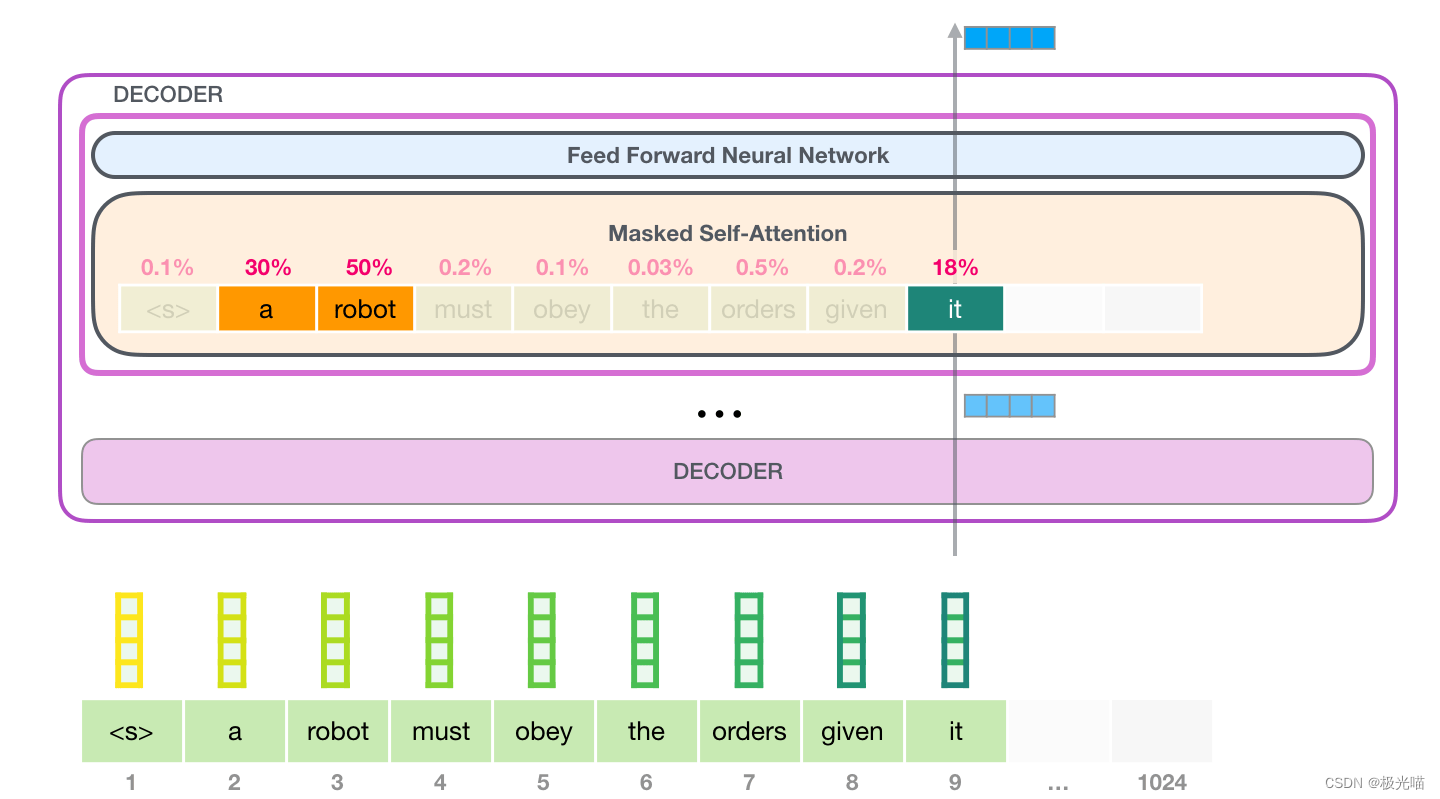
自注意力过程（self-attention）

自注意力机制重要组成部分是三个向量：

• query：在注意力机制中，查询表示当前正在处理的单词或token的表示方式。它用于评估与其他单词之间的相关性。简而言之，查询是我们要关注的中心对象。
• key：键向量是对文本中所有单词的标签或描述。它类似于我们用来在搜索相关单词时进行匹配的内容。在注意力机制中，我们会使用查询和键之间的关系来确定不同单词之间的相关性。
• value：值向量是实际的单词表示方式，通常是通过神经网络学习得到的。一旦我们使用查询和键来评估不同单词之间的相关性，我们将使用这些值向量来计算当前单词的最终表示。值向量会被加权组合，以代表当前单词的含义或重要性。

这三个向量的创建过程在模型实现时非常简单，通过神经网络层的映射即可得到。具体来说，输入数据为token本身（假设64维），而映射后的输入向量可以是192维，此时第0-63维作为q向量，64-127维作为k向量，而128-192维作为v向量。请注意，查询向量、键向量和值向量是为计算和思考注意力机制而抽象出的概念，或者说是我们对模型的学习期望。因为这三个新向量在刚创建时是随机初始化的，没有特殊含义，是经过模型训练分别得到了类似查询、回复、存值等向量功能，一个词向量可以通过它们与其它词向量进行互动来建模词与词之间的相关性。在读者阅读完接下来的全部计算过程之后，就会明白它们名字的由来。

一个粗略的类比是将其想象为在文件柜中搜索。该查询就像一张便签纸，上面写着您正在研究的主题。钥匙就像柜子内文件夹的标签。当你将标签与便签匹配时，我们取出该文件夹的内容，这些内容就是值向量。只不过您不仅要查找一个值，还要从多个文件夹中进行相关内容的查找。

每个文件夹的权重分数是通过查询向量与正在评分的相应单词的键向量的点积计算得出的。点积的公式：a×b=|a|×|b|×cosθ。其意义就是比较两个向量的相关程度，相关性越高，分数越大。注意，点积后需要对结果进行softmax映射得到权重分数，Softmax映射后的分数决定了每个词在句子中某个位置的重要性。

我们将每个值向量乘以它的权重分数并求和——得到我们的自注意力结果。

这种值向量的加权混合会产生一个向量，该向量将 50% 的“注意力”集中在单词robot，30% 的“注意力”集中在单词a，19% 的“注意力”集中在单词it等等。

自注意力计算到此为止。生成的向量是可以发送到前馈神经网络的向量。然而，在实际的实现中，会将输入向量打包成矩阵，以矩阵形式完成此计算，以便更快地在计算机中计算处理，如下图所示

其公式表示如下：

其中, Q、K 和 V 是输入矩阵, 分别代表查询矩阵、键矩阵和值矩阵, dk 是向量维度。Attention公式的作用是通过对 Q 和 K 的相似度进行加权, 来得到对应于输入的 V 的加权和。
具体来说，这个公式分为三个步骤:
（1）计算 Q 和 K 之间的相似度，即  。
（2）由于 Q 和 K 的维度可能很大, 因此需要将其除以  来缩放。这有助于避免在 Softmax 计算时出现梯度消失或梯度爆炸的问题。
(3) 对相似度矩阵进行 Softmax 操作, 得到每个查询向量与所有键向量的权重分布。然后, 将这些权重与值矩阵 V 相乘并相加, 得到自注意力机制的输出矩阵。

多头自注意力层（Multi-heads self-attention）

该论文通过添加一种称为“多头注意力”（Multi-heads self-attention）的机制进一步细化了自注意力层。对于多头注意力，其中有多组查询向量、键向量和值向量，这里把一组q, k, v称之为一个头，Transformer原论文中使用八个注意力头。每组注意力头都是可训练的，经过训练可以扩展模型关注不同位置的能力。

举一个形象的类比：把注意力头类比成小学生，那么多个小学生在学习过程中会形成不同的思维模式，对同样的问题会产生不同的理解。这就是为什么要使用多头的原因，就是希望模型可以从不同的角度思考输入信息，如下图所示。

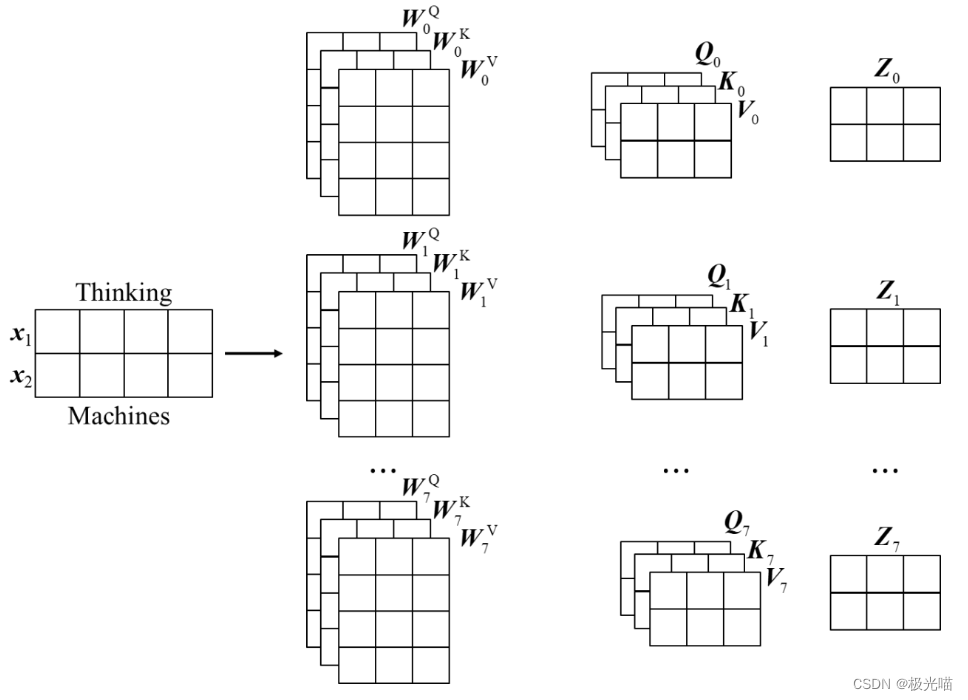
但是，多头注意力机制也给带来了一个问题。如果使用八个头，经过多头注意力机制后会得到8个输出，但是，实际上只需要一个输出结果。所以需要一种方法将这八个输出压缩成一个矩阵，方法也很简单，将它们乘以一个额外的权重矩阵即可。这个操作可以通过一个神经网络层的映射完成，如图：

掩码自注意力机制（Masked Self-Attention）

在本小节中，我们将详细了解Self-Attention如何完成此操作。并讲解它的变体掩码自注意力机制，这在GPT等语言模型中非常常见。以一个简单的自注意力模块举例，它一次只能处理四个token。

自注意力的应用通过三个主要步骤：

1. 为每个输入token创建查询、键和值向量。
2. 对于每个输入token，使用其查询向量针对所有其他键向量进行评分
3. 将值向量与其相关分数相乘后求和。

为每个token创建q,k,v向量的过程如下，其中Wq，Wk和Wv矩阵可以看成神经网络层的参数，也就是说我们可以将token x经过神经网络层的映射得到对应的q,k,v向量。

现在我们有了向量，我们在步骤 2 中使用查询向量和键向量进行点积。当前我们专注于第一个token，因此我们将其查询乘以所有其他键向量，然后再经过softmax的映射从而得出四个token中每个token的权重分数。

现在我们可以将分数乘以值向量。在我们将它们相加之后，得分高的值将构成结果向量中占有重要地位。

如果我们对每个输入执行相同的操作，我们最终会得到一个表示每个token的向量，其中包含该token的适当上下文。然后将它们呈现给Transformer块中的下一个子层（前馈神经网络）：

现在我们已经了解了 Transformer 的 self-attention 步骤，让我们继续看看 masked self-attention。实际上，masked self-attention与自注意力十分相似，除了第 2 步之外。假设模型只有两个token作为输入，并且我们正在观察第二个token。在这种情况下，最后两个token被屏蔽，其对应的权重分数也将是0。

下面我们进行详细的示例计算推导。这种掩蔽通常通过被称为注意掩蔽的矩阵来实现。如下图所示：

我们举个实例，想象一个由四个单词组成的序列（例如“robot must obey orders”）。先可视化其注意力分数的计算：

相乘之后，我们使用注意掩蔽矩阵。它将我们想要屏蔽的单元格设置为 -无穷大或一个非常大的负数（例如 GPT2 中的 -10 亿）：

然后，在每一行上应用 softmax 会产生用于自注意力的实际分数：

这个分数表的含义如下：

• 当模型处理数据集中的第一个示例（第 1 行）时，该示例仅包含一个单词（“机器人”），其 100% 的注意力将集中在该单词上。
• 当模型处理数据集中的第二个示例（第 2 行）时，其中包含单词（“机器人必须”），当模型处理单词“必须”时，48% 的注意力将集中在“机器人”上，而 52% 的注意力将集中在“机器人”上。 %的注意力将集中在“必须”上。

最后，让我们介绍 GPT-2 的masked self-attention。实际上，我们可以让 GPT-2 完全按照 masked self-attention 的方式运行。但在评估过程中，当我们的模型在每次迭代后仅添加一个新单词时，沿着已处理的token的早期路径重新计算自注意力将是低效的。

在本例中，我们处理第一个token（<s>暂时忽略）。

对于单词token“a”，GPT-2 保留它的键向量和值向量。实际上，每个自注意力层都保留每个单词token各自的键向量和值向量：

现在，在下一次迭代中，当模型处理单词”robot“时，它不需要为token “a“生成查询、键和值查询。它只是重用第一次迭代中保存的内容：

这种改进的masked self-attention，可以让q,k,v的计算更加高效快速。最后，我们探讨一个GTP-2自注意力机制中的前向网络（ 全连接神经网络）。

全连接神经网络：这是一个用于进一步处理自注意力模块输出的神经网络。它通常包括两个层（或称为层次）。

• 第一层：这一层通常会有大量的节点（神经元）。节点的数量通常设置为输入token的数量的四倍。例如，如果输入文本的token数量是768，那么第一层将有768 * 4 = 3072 个神经元。这个大的第一层可以用来捕捉输入文本中的各种特征和关系。
• 第二层：第一层的输出被投影回到模型的维度，通常是768（在这个描述中提到了GPT-2模型的维度）。这意味着第二层将输出一个与模型维度相匹配的结果，以便与其他模型部分进行连接和整合。

相关资源

• 自注意力机制详解
• Transformer算法讲解
• OpenAI 的GPT2博文讲解
• OpenAI 的GPT3博文讲解
• Bert，ELMo大语言模型
• 除了 GPT2 之外，还可以查看Hugging Face的pytorch-transformers库，它实现了 BERT、Transformer-XL、XLNet 等前沿 Transformer 模型。
• 本博文的插图来自于Jay Alammar的博客，在此给予真诚的感谢。