从前慢现在也慢

这个屌丝很懒，什么也没留下！

热门标签

笔记-----BFS宽度优先搜索_小杨同学用不同种类的俄罗斯方块填满了一个大小为 n * mn m 的网格图。网格图

作者：从前慢现在也慢 | 2024-04-24 21:57:42

踩

小杨同学用不同种类的俄罗斯方块填满了一个大小为 n * mn m 的网格图。网格图

对于BFS：宽搜第一次搜到就是最小值，并且基于迭代，不会爆栈。

Flood Fill 模型

如果直译的话就是：洪水覆盖，意思就是像是从一个点一圈圈的往外扩散，如果遇见能够连通的就扩散，如果遇见无法联通的就不去扩散，然后再去以扩散出去的点为起点再去扩散。

Flood Fill 可以实现在线性时间复杂度内找到某个点所在的连通块。

例题：

1.AcWing 1097. 池塘计数

农夫约翰有一片 $N * M$ 的矩形土地。

最近，由于降雨的原因，部分土地被水淹没了。

现在用一个字符矩阵来表示他的土地。

每个单元格内，如果包含雨水，则用”W”表示，如果不含雨水，则用”.”表示。

现在，约翰想知道他的土地中形成了多少片池塘。

每组相连的积水单元格集合可以看作是一片池塘。

每个单元格视为与其上、下、左、右、左上、右上、左下、右下八个邻近单元格相连。

请你输出共有多少片池塘，即矩阵中共有多少片相连的 ”W” 块。

输入格式
第一行包含两个整数 $N$ 和 $M$ 。
接下来 $N$ 行，每行包含 $M$ 个字符，字符为 ”W” 或 ”.” ，用以表示矩形土地的积水状况，字符之间没有空格。

输出格式
输出一个整数，表示池塘数目。

数据范围
$1 \leq N, M \leq 1000$

输入样例：

10 12
W........WW.
.WWW.....WWW
....WW...WW.
.........WW.
.........W..
..W......W..
.W.W.....WW.
W.W.W.....W.
.W.W......W.
..W.......W.
1
2
3
4
5
6
7
8
9
10
11

输出样例：

3
1

每次取搜’W’，如果搜到了就去填充连通的所有的’W’并且标记上已经搜过了，然后每发现一滩新的水洼就让答案加1，此题较简单。并且曾经写过DFS的做法：题解博客

BFS:此处使用了便宜量和STL队列，并不和视频中相同

#include<iostream>
#include<queue>
using namespace std;
const int N = 1010;
const int dx[8] = { 0,0,1,-1,1,1,-1,-1 };
const int dy[8] = { 1,-1,0,0,1,-1,1,-1 };
#define pii pair<int,int>
#define x first
#define y second

int n, m;
char g[N][N];
bool st[N][N];

void bfs(int ix, int iy) {
	queue< pii >q;
	q.push({ ix,iy });
	st[ix][iy] = 1;

	while (q.size()) {
		auto t = q.front(); q.pop();
		for (int i = 0; i < 8; i++) {
			int xx = t.x + dx[i], yy = t.y + dy[i];
			if (xx >= 0 && xx < n && yy >= 0 && yy < m && g[xx][yy] == 'W' && !st[xx][yy]) {
				q.push({ xx,yy });
				st[xx][yy] = 1;
			}
		}
	}
}

int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);

	cin >> n >> m;
	for (int i = 0; i < n; i++)cin >> g[i];

	int cnt = 0;
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < m; j++) {
			if (g[i][j] == 'W' && !st[i][j]) {
				bfs(i, j);
				cnt++;
			}
		}
	}

	cout << cnt;
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

2.AcWing 1098. 城堡问题

    1   2   3   4   5   6   7  
   #############################
 1 #   |   #   |   #   |   |   #
   #####---#####---#---#####---#
 2 #   #   |   #   #   #   #   #
   #---#####---#####---#####---#
 3 #   |   |   #   #   #   #   #
   #---#########---#####---#---#
 4 #   #   |   |   |   |   #   #
   #############################
           (图 1)

   #  = Wall   
   |  = No wall
   -  = No wall

   方向：上北下南左西右东。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

图1是一个城堡的地形图。

请你编写一个程序，计算城堡一共有多少房间，最大的房间有多大。

城堡被分割成 $m * n$ 个方格区域，每个方格区域可以有 $0$ ~ $4$ 面墙。
注意：墙体厚度忽略不计。

输入格式
第一行包含两个整数 $m$ 和 $n$ ，分别表示城堡南北方向的长度和东西方向的长度。

接下来 $m$ 行，每行包含 $n$ 个整数，每个整数都表示平面图对应位置的方块的墙的特征。

每个方块中墙的特征由数字 $P$ 来描述，我们用 $1$ 表示西墙， $2$ 表示北墙， $4$ 表示东墙， $8$ 表示南墙， $P$ 为该方块包含墙的数字之和。

例如，如果一个方块的 P 为 $3$ ，则 $3 = 1 + 2$ ，该方块包含西墙和北墙。

城堡的内墙被计算两次，方块 $(1, 1)$ 的南墙同时也是方块 $(2, 1)$ 的北墙。

输入的数据保证城堡至少有两个房间。

输出格式
共两行，第一行输出房间总数，第二行输出最大房间的面积（方块数）。

数据范围
$1 \leq m, n \leq 50,$
$0 \leq P \leq 15$
输入样例：

4 7 
11 6 11 6 3 10 6 
7 9 6 13 5 15 5 
1 10 12 7 13 7 5 
13 11 10 8 10 12 13 
1
2
3
4
5

输出样例：

此题并不困难，只是一个标准的Flood Fill模型题，只是输入的方式让人感到无语。

只要解决了读入的问题，那么这道题就做出来了。
首先题目读入的时候是读入的数字，并且观察题目的条件就会发现有含义的数字都是特殊的 $1 ， 2 ， 4 ， 8$ 分别是二进制的时候第一位，第二位，第三位，第四问为 $1$ 。那么只要读入之后，在后续BFS的过程中不再以传统的判断字符的方式来判定是否能走，而是改为读数字的二进制的位数是否为1来判断就好了，这里使用基础课讲过的lowbit()算法来处理。

并且这里要注意，偏移量要和题目给出的顺序来定。
因为后续遍历取偏移量的时候，如果我们读到了第一位是0，那么就要往西走，其他的方向要另行判定，如果偏移量乱定的话就会乱走。

再注意：编程里面的坐标轴和数学里是不一样的。以下是定偏移量时考虑的坐标轴。
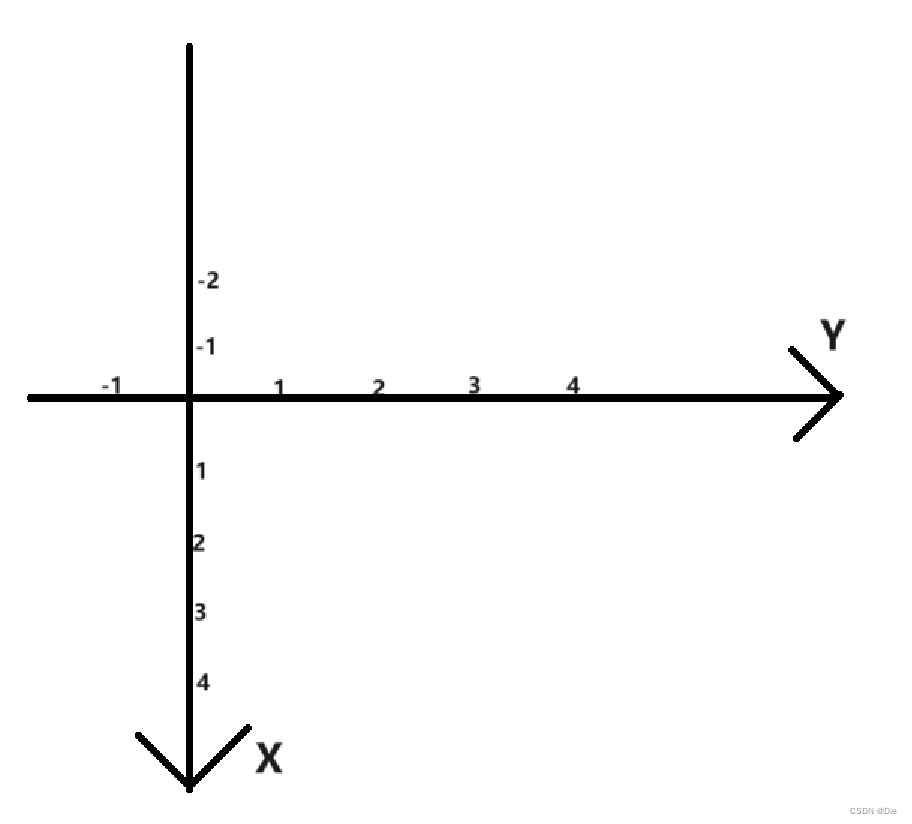
在这里插入图片描述

#include<iostream>
#include<queue>
using namespace std;
const int N = 55;

const int dx[4] = { 0,-1,0,1 };	/*注意这里对偏移量的定义，要严格按照题目给出的西，北，东，南的顺序来*/
const int dy[4] = { -1,0,1,0 };	

#define pii pair<int,int>
#define x first
#define y second

int n, m;
int g[N][N];
bool st[N][N];

int bfs(int ix, int iy) {
	queue<pii>q;
	int s = 0;
	q.push({ ix,iy });
	st[ix][iy] = 1;

	while (q.size()) {
		auto t = q.front();
		s++;	//每次出队，说明有一个空地
		q.pop();

		for (int i = 0; i < 4; i++) {
			int xx = t.x + dx[i], yy = t.y + dy[i];

			//这里g[t.x][t.y] >> i & 1代表寻找当前i这一位是不是一
			//i为0，第1为是1，说明西边有墙，i为1时，第二位为1，说明北边有墙，以此类推
			if (xx >= 0 && xx<n && yy >= 0 && yy<m && !st[xx][yy] && !(g[t.x][t.y]>>i & 1)) {
				q.push({ xx,yy });
				st[xx][yy] = 1;
			}
		}
	}
	return s;
}

int main() {
	cin >> n >> m;
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < m; j++) {
			cin >> g[i][j];
		}
	}

	int cnt = 0;
	int res = 0;
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < m; j++) {
			if (!st[i][j]) {
				res = max(res, bfs(i, j));
				cnt++;
			}
		}
	}

	cout << cnt << endl;
	cout << res << endl;

	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65

3.AcWing 1106. 山峰和山谷

FGD小朋友特别喜欢爬山，在爬山的时候他就在研究山峰和山谷。

为了能够对旅程有一个安排，他想知道山峰和山谷的数量。

给定一个地图，为FGD想要旅行的区域，地图被分为 $n \times n$ 的网格，每个格子 $(i, j)$ 的高度 $w (i, j)$ 是给定的。

若两个格子有公共顶点，那么它们就是相邻的格子，如与 $(i, j)$ 相邻的格子有 $(i - 1, j - 1), (i - 1, j), (i - 1, j + 1), (i, j - 1), (i, j + 1), (i + 1, j - 1), (i + 1, j), (i + 1, j + 1)$ 。

我们定义一个格子的集合 $S$ 为山峰（山谷）当且仅当：

$S$ 的所有格子都有相同的高度。
$S$ 的所有格子都连通。
对于 $s$ 属于 $S$ ，与 $s$ 相邻的 $s'$ 不属于 $S$ ，都有 $w s > w s'$ （山峰），或者 $w s < w s'$ （山谷）。

如果周围不存在相邻区域，则同时将其视为山峰和山谷。

你的任务是，对于给定的地图，求出山峰和山谷的数量，如果所有格子都有相同的高度，那么整个地图即是山峰，又是山谷。

输入格式
第一行包含一个正整数 $n$ ，表示地图的大小。
接下来一个 $n \times n$ 的矩阵，表示地图上每个格子的高度 $w$ 。

输出格式
共一行，包含两个整数，表示山峰和山谷的数量。

数据范围
$1 \leq n \leq 1000,$
$0≤w≤10^9$

输入样例1：

输出样例1：

2 1
1

输入样例2：

输出样例2：

3 3
1

同样是一道Flood Fill模型题，本题需要搜两种连通块的数量。

从题目中需要注意的点：

如果一个点周围既有低的点又有高的点，那这个点既不算山峰也不算山谷
如果一个点周围既没有高的点有没有低的点，那这个点既是山峰又是山谷

搜的时候需要注意的点：

在搜的时候如果扩展到了搜过的点不能直接跳，因为这个点需要用来判别当前点是山峰还是山谷。比如你已经搜过了中间的一个比当前点低部分然后你将其直接跳过，那么这个点就可能变为了没有更低的点的情况，产生错误。

代码：

#include<iostream>
#include<queue>
using namespace std;
const int N = 1010;
const int dx[8] = { 1,0,-1,0,1,1,-1,-1 };	//八连通
const int dy[8] = { 0,1,0,-1,1,-1,1,-1 };
#define pii pair<int,int>
#define x first
#define y second

int n;
int g[N][N];
bool st[N][N];
bool has_higher = 0;
bool has_lower = 0;

void bfs(int ix, int iy) {
	queue<pii>q;
	q.push({ ix,iy });
	st[ix][iy] = 1;

	while (q.size()) {
		auto t = q.front();
		q.pop();

		for (int i = 0; i < 8; i++) {
			int xx = t.x + dx[i], yy = t.y + dy[i];

			//这里先不排除搜过的点，如果排除的话会导致没办法判清楚山峰山谷
			if (xx >= 1 && xx <= n && yy >= 1 && yy <= n) {	

				if (g[xx][yy] > g[t.x][t.y])has_higher = 1;		//有比当前点高的点
				else if (g[xx][yy] < g[t.x][t.y])has_lower = 1;	//有比当前点低的点
				else {						//如果是相等的，也就是连通起来的
					if (!st[xx][yy]) {		//如果没搜过就压入队列
						st[xx][yy] = 1;
						q.push({ xx,yy });
					}
				}
			}
		}
	}
}

int main() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			cin >> g[i][j];
		}
	}


	int valley = 0;	//记录山谷
	int peak = 0;	//记录山峰
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			if (!st[i][j]) {
				bfs(i, j);

				//自动排除了又有高的又有低的点
				if (!has_lower)valley++;	//如果没有更低的点
				if (!has_higher)peak++;		//如果没有更高的点

				has_lower = 0;	//重置
				has_higher = 0;
			}
		}
	}

	cout << peak << " " << valley << endl;
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73

最短路模型

BFS具有最短路的特性，第一次搜出来的解肯定就是最短的最优的。

例题

1.AcWing 1076. 迷宫问题

给定一个 $n \times n$ 的二维数组，如下所示：

int maze[5][5] = {

0, 1, 0, 0, 0,

0, 1, 0, 1, 0,

0, 0, 0, 0, 0,

0, 1, 1, 1, 0,

0, 0, 0, 1, 0,

};
1
2
3
4
5
6
7
8
9
10
11
12
13

它表示一个迷宫，其中的 $1$ 表示墙壁， $0$ 表示可以走的路，只能横着走或竖着走，不能斜着走，要求编程序找出从左上角到右下角的最短路线。

数据保证至少存在一条从左上角走到右下角的路径。

输入格式
第一行包含整数 $n$ 。
接下来 $n$ 行，每行包含 $n$ 个整数 $0$ 或 $1$ ，表示迷宫。

输出格式
输出从左上角到右下角的最短路线，如果答案不唯一，输出任意一条路径均可。

按顺序，每行输出一个路径中经过的单元格的坐标，左上角坐标为 $(0, 0)$ ，右下角坐标为 $(n - 1, n - 1)$ 。

数据范围
$0 \leq n \leq 1000$
输入样例：

输出样例：

此题要求记录并输出最短路径，因为BFS自己第一次搜出来就一定是一个最短路径，所以直接使用数组记录路径就可以。

要不然就是倒着记录路径正着搜，然后倒着输出，要不然就是倒着搜正着输出。

并且题目要求输出坐标，所以要用pair来存路径。

代码：

#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
#define pii pair<int,int>
#define x first
#define y second
const int N = 1010;
const int dx[4] = { 0,1,0,-1 };
const int dy[4] = { 1,0,-1,0 };

int n;
int g[N][N];    
pii next[N][N]; //pair存路径，因为要求输出坐标，同时兼顾判断搜没搜过某点的功能

void bfs(int ix, int iy) {
	queue<pii>q;
	q.push({ ix,iy });
	
	memset(next, -1, sizeof next);  //初始化为-1，用于之后判定是否搜过某点
	
	next[ix][iy] = { 0,0 }; //标记上起点

	while (q.size()) {
		auto t = q.front();
		q.pop();
		
		for (int i = 0; i < 4; i++) {
			int xx = t.x + dx[i], yy = t.y + dy[i];
			                                             //只有0能走
			if (xx >= 0 && xx < n && yy >= 0 && yy < n && !g[xx][yy] && next[xx][yy].x == -1) {
				q.push({ xx,yy });
				next[xx][yy] = t;   //记录路径
			}
		}
	}
}

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);

	cin >> n;
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			cin >> g[i][j];
		}
	}

	bfs(n - 1, n - 1);  //倒着搜，从终点找起点，这样得到的路径记录是正着的

	pii end(0, 0);  //从0 0开始
	while (1) {
		cout << end.x << " " << end.y << endl;
		if (end.x == n - 1 && end.y == n - 1)break; //当输出完终点之后就break
		end = next[end.x][end.y];    //转移到下一个路径
	}

	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

AcWing 188. 武士风度的牛

农民 John 有很多牛，他想交易其中一头被 Don 称为 The Knight 的牛。

这头牛有一个独一无二的超能力，在农场里像 Knight 一样地跳（就是我们熟悉的象棋中马的走法）。

虽然这头神奇的牛不能跳到树上和石头上，但是它可以在牧场上随意跳，我们把牧场用一个 $x ， y$ 的坐标图来表示。

这头神奇的牛像其它牛一样喜欢吃草，给你一张地图，上面标注了 The Knight 的开始位置，树、灌木、石头以及其它障碍的位置，除此之外还有一捆草。

现在你的任务是，确定 The Knight 要想吃到草，至少需要跳多少次。

The Knight 的位置用 K来标记，障碍的位置用 * 来标记，草的位置用 H来标记。

这里有一个地图的例子：

             11 | . . . . . . . . . .
             10 | . . . . * . . . . . 
              9 | . . . . . . . . . . 
              8 | . . . * . * . . . . 
              7 | . . . . . . . * . . 
              6 | . . * . . * . . . H 
              5 | * . . . . . . . . . 
              4 | . . . * . . . * . . 
              3 | . K . . . . . . . . 
              2 | . . . * . . . . . * 
              1 | . . * . . . . * . . 
              0 ----------------------
                                    1 
                0 1 2 3 4 5 6 7 8 9 0 
1
2
3
4
5
6
7
8
9
10
11
12
13
14

The Knight 可以按照下图中的 $A, B, C, D$ … 这条路径用 $5$ 次跳到草的地方（有可能其它路线的长度也是 $5$ ）：

             11 | . . . . . . . . . .
             10 | . . . . * . . . . .
              9 | . . . . . . . . . .
              8 | . . . * . * . . . .
              7 | . . . . . . . * . .
              6 | . . * . . * . . . F<
              5 | * . B . . . . . . .
              4 | . . . * C . . * E .
              3 | .>A . . . . D . . .
              2 | . . . * . . . . . *
              1 | . . * . . . . * . .
              0 ----------------------
                                    1
                0 1 2 3 4 5 6 7 8 9 0
1
2
3
4
5
6
7
8
9
10
11
12
13
14

注意：数据保证一定有解。

输入格式
第 $1$ 行：两个数，表示农场的列数 $C$ 和行数 $R$ 。

第 $2.. R + 1$ 行: 每行一个由 $C$ 个字符组成的字符串，共同描绘出牧场地图。

输出格式
一个整数，表示跳跃的最小次数。

数据范围
$1 \leq R, C \leq 150$
输入样例：

10 11
..........
....*.....
..........
...*.*....
.......*..
..*..*...H
*.........
...*...*..
.K........
...*.....*
..*....*..
1
2
3
4
5
6
7
8
9
10
11
12

输出样例：

5
1

#include<iostream>
#include<cstring>
#include<queue>
#define x first
#define y second
#define pii pair<int,int>
using namespace std;
const int N = 160;
const int dx[8] = { 1,1,-1,-1,2,2,-2,-2 };  //走日字
const int dy[8] = { 2,-2,2,-2,1,-1,1,-1 };

int n, m;
char g[N][N];
int dis[N][N];  //记录距离并且标记是否走过

int bfs() {
	memset(dis, -1, sizeof dis);    //初始化

	int ix, iy;
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < m; j++) {
			if (g[i][j] == 'K')ix = i, iy = j;  //找起点
		}
	}

	queue<pii>q;
	q.push({ ix,iy });
	dis[ix][iy] = 0;    //起点距离设为0

	while (q.size()) {
		auto t = q.front();
		if(g[t.x][t.y] == 'H')return dis[t.x][t.y];
		q.pop();

		for (int i = 0; i < 8; i++) {
			int xx = t.x + dx[i], yy = t.y + dy[i];

			if (xx >= 0 && xx < n && yy >= 0 && yy < m && g[xx][yy] != '*' && dis[xx][yy] == -1) {
				dis[xx][yy] = dis[t.x][t.y] + 1;    //更新距离
				q.push({xx,yy});
			}
		}
	}
}

int main() {
	cin >> m >> n;  //先读入列再读入行
	for (int i = 0; i < n; i++) cin >> g[i];

	cout << bfs() << endl;
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

AcWing 1100. 抓住那头牛

农夫知道一头牛的位置，想要抓住它。

农夫和牛都位于数轴上，农夫起始位于点 $N$ ，牛位于点 $K$ 。

农夫有两种移动方式：

从 X 移动到 $X - 1$ 或 $X + 1$ ，每次移动花费一分钟
从 X 移动到 $2 * X$ ，每次移动花费一分钟假设牛没有意识到农夫的行动，站在原地不动。

农夫最少要花多少时间才能抓住牛？

输入格式
共一行，包含两个整数 $N$ 和 $K$ 。

输出格式
输出一个整数，表示抓到牛所花费的最少时间。

数据范围
$0≤N,K≤10^5$

输入样例：

5 17
1

输出样例：

4
1

利用BFS的最短路的特性，直接搜遍所有情况，最终一定能够得到一个最短距离。

#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
const int N = 1e5 + 10;

int n, k;
int q[N];
int dis[N];

int bfs() {
	memset(dis, -1, sizeof dis);

	dis[n] = 0;
	queue<int>q;
	q.push(n);

	while (q.size()) {
		int t = q.front();
		q.pop();

		if (t == k)return dis[t];		//找到终点了，返回距离

		if (t + 1 < N && dis[t + 1] == -1) {	//如果还可以前进一步
			dis[t + 1] = dis[t] + 1;
			q.push({ t + 1 });
		}
		if (t - 1 >= 0 && dis[t - 1] == -1) {	//如果还可以后退一步
			dis[t - 1] = dis[t] + 1;
			q.push({ t - 1 });
		}
		if (t * 2 < N && dis[t * 2] == -1) {	//如果可以乘2
			dis[t * 2] = dis[t] + 1;
			q.push({ t * 2 });
		}
	}
}

int main() {
	cin >> n >> k;

	cout << bfs();

	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

多源最短路

AcWing.173.矩阵距离

给定一个 $N$ 行 $M$ 列的 01 矩阵 $A ， A [i] [j]$ 与 $A [k] [l]$ 之间的曼哈顿距离定义为：

$d i s t (A [i] [j], A [k] [l]) = ∣ i - k ∣ + ∣ j - l ∣$
输出一个 $N$ 行 $M$ 列的整数矩阵 $B$ ，其中：

$B [i] [j] = min 1 \leq x \leq N, 1 \leq y \leq M, A [x] [y] = 1 d i s t (A [i] [j], A [x] [y])$
输入格式
第一行两个整数 $N, M$ 。

接下来一个 $N$ 行 $M$ 列的 01 矩阵，数字之间没有空格。

输出格式
一个 $N$ 行 $M$ 列的矩阵 $B$ ，相邻两个整数之间用一个空格隔开。

数据范围
$1 \leq N, M \leq 1000$

输入样例：

输出样例：

本题的意思就是求多个起点到达离其最近的1的距离。

可以设置一个虚拟的起点，然后让虚拟起点和所有的起点的边权为 $0$ ，之后进行BFS。
在本题中，我们要求的是所有点到达 $1$ 的最小距离，那么我们就可以直接把所有的 $1$ 点的距离设为 $0$ ，然后存入队列中，再用BFS来求出所有距离 $1$ 点最近的 $0$ 点的距离。

代码：

#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
const int N = 1010;
#define pii pair<int,int>
#define x first
#define y second
const int dx[4] = {1,0,-1,0};
const int dy[4] = {0,1,0,-1};
int dis[N][N];
char g[N][N];
int n,m;

void bfs(){
    memset(dis,-1,sizeof dis);
    
    queue<pii>q;
    for(int i = 1;i <= n;i++)
        for(int j = 1;j <= m;j++)
            if(g[i][j] == '1'){
                dis[i][j] = 0;
                q.push({i,j});
            }
    
    while(q.size()){
        auto t = q.front();
        q.pop();
        
        for(int i = 0;i < 4;i++){
            int xx = t.x + dx[i],yy = t.y + dy[i];
            if(xx>=1&&xx<=n&&yy>=1&&yy<=m&&dis[xx][yy] == -1){
                dis[xx][yy] = dis[t.x][t.y] + 1;
                q.push({xx,yy});
            }
        }
    }
}


int main(){
    cin >> n >> m;
    for(int i = 1;i <= n;i++)
        for(int j = 1;j <= m;j++)
            cin >> a[i][j];
            
    bfs();
    
    for(int i = 1;i <= n;i++)
    {
        for(int j = 1;j <= m;j++)
            cout << dis[i][j] << " ";
            
        puts("");    
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

最小路数模型

对于最小步数模型，常用的方法就是用哈希存状态来压入队列，而不用原本的矩阵，并且基本的操作也映射到哈希存的状态上。

Acwing.1107.魔板

Rubik 先生在发明了风靡全球的魔方之后，又发明了它的二维版本——魔板。

这是一张有 8 个大小相同的格子的魔板：

我们知道魔板的每一个方格都有一种颜色。

这 8 种颜色用前 8 个正整数来表示。

可以用颜色的序列来表示一种魔板状态，规定从魔板的左上角开始，沿顺时针方向依次取出整数，构成一个颜色序列。

对于上图的魔板状态，我们用序列 (1,2,3,4,5,6,7,8) 来表示，这是基本状态。

这里提供三种基本操作，分别用大写字母 A，B，C 来表示（可以通过这些操作改变魔板的状态）：

A：交换上下两行；
B：将最右边的一列插入到最左边；
C：魔板中央对的4个数作顺时针旋转。

下面是对基本状态进行操作的示范：

A：

B：

C：

对于每种可能的状态，这三种基本操作都可以使用。

你要编程计算用最少的基本操作完成基本状态到特殊状态的转换，输出基本操作序列。

注意：数据保证一定有解。

输入格式
输入仅一行，包括 8 个整数，用空格分开，表示目标状态。

输出格式
输出文件的第一行包括一个整数，表示最短操作序列的长度。

如果操作序列的长度大于0，则在第二行输出字典序最小的操作序列。

数据范围
输入数据中的所有数字均为 1 到 8 之间的整数。

输入样例：

2 6 8 4 5 7 3 1
1

输出样例：

7
BCABCCB
1
2

对于本题的矩阵，直接哈希成排列的数字12345678，并且从这个纬度上考虑问题。

如果执行A操作，就会使其变为87654321
如果执行B操作，就会使其变为41236785
如果执行C操作，就会使其变为17245368

只需要确定哪个状态是由哪个状态转移过来的，记录下来之后只需要从终点倒推到起点就行了。

对于字典序，只需要保证是按照 ABC的顺序进行执行的，而只要按照A，B，C的执行顺序去扫，就能够保证字典序。
因为BFS的时候在前一个状态搜完搜到 $B$ 之后，之后的状态就不可能再搜到C，因为之前搜到 $B$ 的时候就已经标注好这个状态了。

代码：

#include<iostream>
#include<queue>
#include<unordered_map>
#include<algorithm>
using namespace std;

char g[2][4];
unordered_map<string,int>dis;
unordered_map<string,pair<char,string>>pre;
queue<string>q;

void changeTog(string st){	//将矩阵更新成字符串的模样
	for(int i = 0;i < 4;i++)g[0][i] = st[i];
	for(int i = 3,j = 4;i >= 0;i--,j++)g[1][i] = st[j];
}

string changeToString(){	//将矩阵对应的字符串转化出来
	string res;
	for(int i = 0;i < 4;i++)res += g[0][i];
	for(int i = 3;i >= 0;i--)res += g[1][i];

	return res;
}

//3个操作
string A(string st){	
	changeTog(st);		//每次先更新矩阵
	for(int i = 0;i < 4;i++)swap(g[0][i],g[1][i]);//直接交换上下两行
	return changeToString();
}

string B(string st){
	changeTog(st);
	char c1 = g[0][3],c2 = g[1][3];

	for(int i = 3;i > 0;i--){	
	    g[0][i] = g[0][i-1];	
		g[1][i] = g[1][i-1];
	}

	g[0][0] = c1;
	g[1][0] = c2;
	return changeToString();
}

string C(string st){
	changeTog(st);

	//转圈
	char c = g[0][1];
	g[0][1] = g[1][1];
	g[1][1] = g[1][2];
	g[1][2] = g[0][2];
	g[0][2] = c;

	return changeToString();
}

void bfs(string start,string end){
	q.push(start);
	dis[start] = 0;

	while(q.size()){
		auto t = q.front();
		q.pop();

		if(t == end)return;	//搜到终点状态了就返回

		string next[3];		//提取出三种操作得来的状态
		next[0] = A(t);
		next[1] = B(t);
		next[2] = C(t);

		//按ABC顺序搜三种状态
		for(int i = 0;i < 3;i++){
			if(dis.count(next[i]) == 0){
			    
				dis[next[i]] = dis[t] + 1;
				pre[next[i]] = {char(i + 'A'),t};
				
				if(next[i] == end)break;
				
				q.push(next[i]);
			}
		}
	}
}

int main(){
	int x;string start,end;
	
	for(int i = 0;i < 8;i++){
		cin >> x;
		end += (x + '0');
	}
	start = "12345678";

	bfs(start,end);

	cout << dis[end] << endl;

	string res;
	while(end != start){
		res += pre[end].first;
		end = pre[end].second;
	}

	reverse(res.begin(),res.end());

	//如果步数不为0才输出
	if(res.size())cout << res << endl;

	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114

双端队列广搜

使用双端队列来维持一个队列中的单调性和两段性。

AcWing.175.电路维修

达达是来自异世界的魔女，她在漫无目的地四处漂流的时候，遇到了善良的少女翰翰，从而被收留在地球上。

翰翰的家里有一辆飞行车。

有一天飞行车的电路板突然出现了故障，导致无法启动。

电路板的整体结构是一个 R 行 C 列的网格 $（ R, C \leq 500 ）$ ，如下图所示。

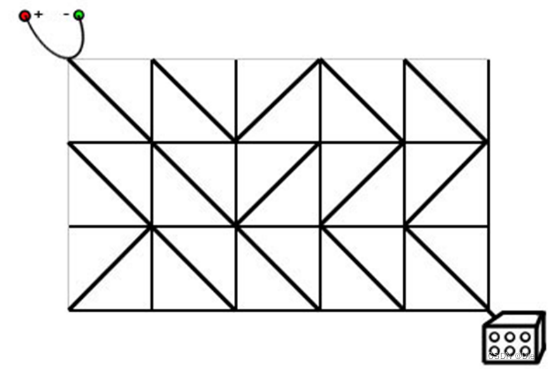
在这里插入图片描述

每个格点都是电线的接点，每个格子都包含一个电子元件。

电子元件的主要部分是一个可旋转的、连接一条对角线上的两个接点的短电缆。

在旋转之后，它就可以连接另一条对角线的两个接点。

电路板左上角的接点接入直流电源，右下角的接点接入飞行车的发动装置。

达达发现因为某些元件的方向不小心发生了改变，电路板可能处于断路的状态。

她准备通过计算，旋转最少数量的元件，使电源与发动装置通过若干条短缆相连。

不过，电路的规模实在是太大了，达达并不擅长编程，希望你能够帮她解决这个问题。

注意：只能走斜向的线段，水平和竖直线段不能走。

输入格式
输入文件包含多组测试数据。

第一行包含一个整数 T，表示测试数据的数目。

对于每组测试数据，第一行包含正整数 R 和 C，表示电路板的行数和列数。

之后 R 行，每行 C 个字符，字符是"/“和”"中的一个，表示标准件的方向。

输出格式
对于每组测试数据，在单独的一行输出一个正整数，表示所需的最小旋转次数。

如果无论怎样都不能使得电源和发动机之间连通，输出NO SOLUTION。

数据范围
$1 \leq R, C \leq 500,$
$1 \leq T \leq 5$

输入样例：

1
3 5
\\/\\
\\///
/\\\\
1
2
3
4
5

输出样例：

1
1

样例解释
样例的输入对应于题目描述中的情况。

只需要按照下面的方式旋转标准件，就可以使得电源和发动机之间连通。

对于这道题，就相当于有线连着的路径的边权是0，没有连起来的需要转一下电线才能走过去，所以边权是1。
那么就相当于在这个边权为0或1的图上搜最短路的问题。

在这里使用双端队列，如果搜到了边权为0的点，就压入队头，如果搜到了边权为1的点，就压入队尾。在这种条件下，可以始终维护队列的两段性和单调性。

并且应注意，如果当前点的横纵坐标的和是偶数，那么就一定到不了横纵坐标之和为奇数的点，反之同理。

CODE:

#include <iostream>
using namespace std;
#define pii pair<int, int>
const int N = 510, M = N * N;
const int dx[4] = {-1,-1,1,1};
const int dy[4] = {-1,1,1,-1};

int n, m;
char g[N][N];
int dis[N][N];
bool st[N][N];

int bfs(){
    memset(st,0,sizeof st);
    memset(dis,0x3f,sizeof dis);

    deque<pii>q;
    q.push_back({0,0});
    dis[0][0] = 0;    

    char c[5] = "\\/\\/";//这里存的是应该是什么样的方向才是正确的

    int ix[4] = {-1,-1,0,0},iy[4] = {-1,0,0,-1};//扩展图的下标

    while(q.size()){
        auto t = f.front();
        q.pop_front();

        int x = t.first,y = t.second;
        if(x == n && y == m)return dis[x][y];

        if(st[x][y])continue;
        st[x][y] = 1;

        for(int i = 0;i < 4;i++){
            int a = x + dx[i],b = y + dy[i];

            if(a >= 0 && a <= n && b >= 0 && b <= m){
                int ga = x + ix[i],gb = y + iy[i];

                int w = (g[ga][gb] != c[i]);

                if(g[ga][gb] + w <= dis[a][b]){
                    dis[a][b] = d;

                    if(!w)q.push_front({a,b});  //如果是正确的字符，即边权为0，那么压入队头
                    else q.push_back({a,b});    //否则压入队尾
                }
            }
        }
    }
    return -1;
}

int main()
{
    int t;
    cin >> t;
    while (t--)
    {
        cin >> n >> m;
        for (int i = 0; i < n; i++)
                cin >> g[i];

        if (n + m & 1) puts("NO SOLuTION\n");
        else cout << bfs() << endl;
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69

双向广搜

顾名思义从两个方向同时扩展来搜，是一种BFS的优化方法，一般适用于最小步数模型。

AcWing.190.字符串变换

已知有两个字串 A, B 及一组字串变换的规则（至多 6 个规则）:

A1→B1
A2→B2
…

规则的含义为：在 A 中的子串 A1 可以变换为 B1、A2 可以变换为 B2…。

例如：A＝abcd B＝xyz

变换规则为：

abc → xu ud → y y → yz

则此时，A 可以经过一系列的变换变为 B，其变换的过程为：

abcd → xud → xy → xyz

共进行了三次变换，使得 A 变换为 B。

注意，一次变换只能变换一个子串，例如 A＝aa B＝bb

变换规则为：

a → b

此时，不能将两个 a 在一步中全部转换为 b，而应当分两步完成。

输入格式
输入格式如下：

A B

A1 B1

A2 B2

… …
1
2
3
4
5
6
7

第一行是两个给定的字符串 A 和 B。

接下来若干行，每行描述一组字串变换的规则。

所有字符串长度的上限为 20。

输出格式
若在 10 步（包含 10 步）以内能将 A 变换为 B ，则输出最少的变换步数；否则输出 NO ANSWER!。

输入样例：

abcd xyz
abc xu
ud y
y yz
1
2
3
4

输出样例：

3
1

#include<bits/stdc++.h>
using namespace std;

string a[6],b[6];
int n;

int extend(queue<string> &q,unordered_map<string,int> &da,unordered_map<string,int> &db,string a[],string b[]){
    int d = da[q.front()];

    while(q.size() && da[q.front()] == d){  //要搜的是这一层，即距离相等的队列中的这些状态
        auto t = q.front();
        q.pop();

        for(int i = 0;i < n;i++){       //枚举规则

            for(int j = 0;j < t.size();j++){    //枚举起点

                if(t.substr(j,a[i].size()) == a[i]){    //如果可以扩展

                    string st = t.substr(0,j) + b[i] + t.substr(j + a[i].size());

                    if(db.count(st))return da[t] + db[st] + 1;  //如果之前被另一边搜到过就返回

                    if(da.count(st))continue;   //如果之前被自己搜到过，就continue

                    da[st] = da[t] + 1;
                    q.push(st);
                }
            }
        }
    }
    return 11;
}

int bfs(string A,string B){
    if(A == B)return 0; //特判
    
    queue<string>qa,qb;
    
    qa.push(A);
    qb.push(B);
    
    unordered_map<string,int>dis_a;
    unordered_map<string,int>dis_b;
    
    dis_a[A] = 0;
    dis_b[B] = 0;

    int step = 0;
    while(qa.size() && qb.size()){//如果有一边已经搜遍了还没有找到解,就说明一定没有解 
        int t;
        if(qa.size() <= qb.size())t = extend(qa,dis_a,dis_b,a,b);//如果a的能够扩展的范围更小就扩展a
        else t = extend(qb,dis_b,dis_a,b,a);      //反之扩展b,反着搜也应该反着使用规则

        if(t <= 10)return t; 
        step ++;
        if(step > 10)return 11; //步数大于10直接返回
    }

    return 11;//返回一个大于10的值
}

int main(){
    string A,B;cin >> A >> B;

    while(cin >> a[n] >> b[n])n++;

    int step = bfs(A,B);
    if(step > 10)cout << "NO ANSWER!\n";
    else cout << step;

    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73

A*

只有在搜索的范围非常广大的时候，A*算法才会有效果。

首先，把BFS中的队列换成优先队列。
在存的时候要存下真实距离和估价距离。

真实距离就是从起点到当前点的真实距离
估价距离就是从起点到当前点的估计距离

优先队列排序的时候就按照两个距离相加从小到大排序，即小根堆。
然后去搜索所有的邻边，当终点第一次出队的时候就结束算法。

在A* 算法中，只要所有的边权都是非负的就可以，并且必须满足每一个点从当前位置到终点的估计距离一定是小于等于从当前位置到终点的真实距离的。
并且A* 算法只能保证终点的距离最小的，并不能保证中间点的距离是最小的。

AcWing.179.八数码

在一个 3×3 的网格中，1∼8 这 8 个数字和一个 x 恰好不重不漏地分布在这 3×3 的网格中。

例如：

在游戏过程中，可以把 x 与其上、下、左、右四个方向之一的数字交换（如果存在）。

我们的目的是通过交换，使得网格变为如下排列（称为正确排列）：

例如，示例中图形就可以通过让 x 先后与右、下、右三个方向的数字交换成功得到正确排列。

交换过程如下：

1 2 3   1 2 3   1 2 3   1 2 3
x 4 6   4 x 6   4 5 6   4 5 6
7 5 8   7 5 8   7 x 8   7 8 x
1
2
3

把 x 与上下左右方向数字交换的行动记录为 u、d、l、r。

现在，给你一个初始网格，请你通过最少的移动次数，得到正确排列。

输入格式
输入占一行，将 3×3 的初始网格描绘出来。

例如，如果初始网格如下所示：

则输入为：1 2 3 x 4 6 7 5 8

输出格式
输出占一行，包含一个字符串，表示得到正确排列的完整行动记录。

如果答案不唯一，输出任意一种合法方案即可。

如果不存在解决方案，则输出 unsolvable。

输入样例：

2 3 4 1 5 x 7 6 8
1

输出样例

ullddrurdllurdruldr
1

对于八数码问题，只有转化出来的一维的逆序对的数量是偶数则有解，是奇数则无解。这个结论对于任何奇数n*n的数码问题都成立。

如果使用A*算法就需要设计出估价函数，那么如何设计？
首先，在八数码问题中，如果x和任何一个数进行互换，那么就只会改变一个数的位置，在这里把估价函数设置为当前数字的目标距离和他当前的真实距离的曼哈顿距离之和。那么在移动的过程中，曼哈顿距离一定是不断减小的，那么估价函数就一定满足小于等于从当前位置到达其目标位置的距离

CODE:

#include<bits/stdc++.h>
using namespace std;
#define pis pair<int,string>
const int dx[4] = {-1,0,1,0};
const int dy[4] = {0,1,0,-1};

int f(string st){   //估价函数
    int res = 0;
    for(int i = 0;i < st.size();i++){
        if(st[i] != 'x'){
            int t = st[i] - '1';
            res += abs(i/3 - t/3) + abs(i%3 - t%3);
        }
    }
    return res;
}

string bfs(string st){
    string ed = "12345678x";
    char op[] = "urdl";

    unordered_map< string,int >dis; //每个状态对应的步数
    unordered_map< string,pair<char,string> > pre;  //记录前一个状态

    priority_queue< pis,vector<pis>,greater<pis> >heap; //优先队列广搜

    dis[st] = 0;            //启始状态距离为0
    heap.push({0+f(st),st});  //压入本身距离加估价值和状态

    while(heap.size()){
        auto t = heap.top();
        heap.pop();

        string st = t.second;   //取出状态
        if(st == ed)break;      //如果已经搜到了就break

        int x,y;
        for(int i = 0;i < 9;i++){
            if(st[i] == 'x'){
                x = i/3,y = i % 3;  //取坐标，映射到二维
                break;
            }
        }

        string source = st; //先保存下来当前的状态
        for(int i = 0;i < 4;i++){
            int a = x + dx[i],b = y + dy[i];    //扩展点
            
            if(a >= 0 && a < 3 && b >= 0 && b < 3){
                
                st = source;   //先复原状态
                swap(st[x*3 + y],st[a*3 + b]);  //再把三维转化为一维，然后进行数字交换
                
                if(dis.count(st) == 0 || dis[st] > dis[source] + 1){//如果没有搜过这个状态或者距离更小
                    dis[st] = dis[source] + 1;  //更新距离
                    pre[st] = {op[i],source};   //记录前一个状态和转换过来的操作
                    heap.push({dis[st] + f(st),st});    //把本身距离加估价值和状态压入队列
                }
            }
        }
    }

    string res;
    while(ed != st){
        res += pre[ed].first;
        ed = pre[ed].second;
    }
    reverse(res.begin(),res.end());

    return res;
}

int main(){
    string st,se;//se只存数，st存包含x的原串
    char c;

    while(cin >> c){
        st += c;
        if(c != 'x')se += c;
    }

    int cnt = 0;        //求逆序对数量
    for(int i = 0;i < 8;i++){
        for(int j = i;j < 8;j++){
            if(se[i] > se[j])cnt++;
        }
    }

    if(cnt & 1)cout << "unsolvable\n";  //如果逆序对是奇数，就无解
    else cout << bfs(st) << endl;

    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93

AcWing.178.第K短路

给定一张 N 个点（编号 1,2…N），M 条边的有向图，求从起点 S 到终点 T 的第 K 短路的长度，路径允许重复经过点或边。

注意：每条最短路中至少要包含一条边。

输入格式
第一行包含两个整数 N 和 M。

接下来 M 行，每行包含三个整数 A,B 和 L，表示点 A 与点 B 之间存在有向边，且边长为 L。

最后一行包含三个整数 S,T 和 K，分别表示起点 S，终点 T 和第 K 短路。

输出格式
输出占一行，包含一个整数，表示第 K 短路的长度，如果第 K 短路不存在，则输出 −1。

数据范围
$1 \leq S, T \leq N \leq 1000,$
$0 \leq M \leq 104,$
$1 \leq K \leq 1000,$
$1 \leq L \leq 100$

输入样例：

输出样例：

14
1

我们要求第K短路，就是从所有点到达终点的路径中，选出一个第K短的那条路径。
那么就只需要反着从终点扩展到每个点，找到第K短的路径就可以了。

在这里就用dijkstra跑出来的所有从起点跑到每个点的距离为每个点的估价距离。因为这样的估价距离一定是小于等于每个点到达终点的实际距离的，并且其已经尽可能的接近于真实距离。

从队列中弹出的第K个就是第K小，证明见AcWing算法提高课。

#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
const int M = 2e4+10;   //因为要存正反边，所以开两倍

#define pii pair<int,int>
#define piii pair<int,pii>

int n,m,s,t,k;
int h[N],e[M],w[M],ne[M],idx;
int rh[N];  //反向邻接表表头
int dis[N];
int cnt[N]; //记录每个点在Astar算法中弹出的次数
bool st[N];

void add(int h[],int a,int b,int c){
    e[idx] = b,w[idx] = c,ne[idx] = h[a],h[a] = idx++;
}

void dijkstra(){    //dijkstra算法进行估价，估价结果存入dis[]数组中
    priority_queue< pii,vector<pii>,greater<pii> > heap;
    heap.push({0,t});

    memset(dis,0x3f,sizeof dis);
    dis[t] = 0;

    while(heap.size()){
        auto tt = heap.top();
        heap.pop();

        int ver = tt.second;
        if(st[ver])continue;
        st[ver] = 1;

        for(int i = rh[ver];i != -1;i = ne[i]){
            int j = e[i];
            if(dis[j] > dis[ver] + w[i]){

                dis[j] = dis[ver] + w[i];
                heap.push({dis[j],j});
            }
        }
    }    
}

int astar(){
    priority_queue<piii,vector<piii>,greater<piii> >heap;
    heap.push({dis[s],{0,s}});  //{ 真实距离+估价距离 ， { 真实距离 ， 当前点 } }

    while(heap.size()){
        auto tt = heap.top();
        heap.pop();

        int ver = tt.second.second,distance = tt.second.first;  //取出点和距离

        cnt[ver]++; //ver点被弹出，故记录一次

        if(cnt[t] == k)return distance; //当终点被弹出第k次的时候，那么就说明搜到了第k短路

        for(int i = h[ver];i != -1;i = ne[i]){
            int j = e[i];
            if(cnt[j] < k)  //限制cnt[j]小于k，任何一个点出现大于等于k次时入队是无意义的
                heap.push({distance + w[i] + dis[j],{distance + w[i],j}});
        }
    }

    return -1;
}

int main(){
    cin >> n >> m;
    memset(h,-1,sizeof h);
    memset(rh,-1,sizeof rh);

    for(int i = 0;i < m;i++){
        int a,b,c;  
        cin >> a >> b >> c;
        add(h,a,b,c);   //建正向边
        add(rh,b,a,c);  //建反向边
    }

    cin >> s >> t >> k;
    if(s == t)k++;  //如果一开始起点和终点相等，k++
                    //因为题目要求每条最短路都最少有一条边，所以这个边不算。

    dijkstra();
    cout << astar() << endl;

    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/从前慢现在也慢/article/detail/481748