devbox
从前慢现在也慢
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

【数据结构Note2】- 链表 - 基础到实战-入门到应用_将长度为m的线性链表链接在长度为n

作者：从前慢现在也慢 | 2024-05-07 18:45:20

赞

踩

将长度为m的线性链表链接在长度为n

文章目录

1. 线性表

线性表(linear list)是n个具有相同特性的数据元素的有限序列。线性表在逻辑上是线性结构。数据元素的前一个数据元素叫直接前趋，数据元素的后一个结点叫直接后继。常见的线性表有:顺序表、链表、栈、队列、字符串…也就说是连续的一条直线。在计算机内，线性表有两种基本的存储结构：线性表顺序存储结构和线性表链式存储结构，也就是常说的链表和顺序表。

线性表顺序存储结构：数组实现，

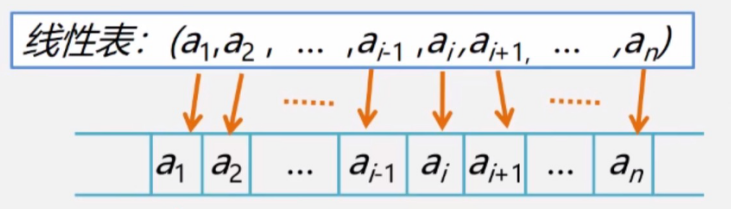
image-20220908093246780

线性表链式存储结构：链表实现

image-20220522160641917

前面讲的顺序表（数组实现），要求逻辑相邻的元素在物理内存上也相邻，具有随机存取数据的强优点，但数组内存空间的连续性导致了其插入删除操作需要移动大量元素。本次讲的线性表的链式存储（链表），不要求逻辑上相邻的元素在物理位置上相邻，而是通过指针来反映数据之间的逻辑关系，插入删除操作简单，但非随机存取。

顺序表有静态顺序表（数组长度一定）和动态顺序表（数组长度动态申请）

链表有静态链表（数组实现）和动态链表（指针实现），这里主要讲解动态链表

2. 线性表的链式存储（链表）

链表其存储结构特点是物理存储单元上任意，数据元素由链表中的指针依次链接而成，指针就作为数据元素之间的逻辑关系的映像。链表的基本单位是结点，结点包括两个部分：存储数据元素的数据域和存储结点地址的指针域。链表有很多种不同的类型：单向或者双向，带头或者不带头，循环或者非循环自由组合等八类链表（2*2*2）。

3. 链表分类：

3.1单向链表与双向链表：

单向链表：只有一个指针域，指向直接后继

image-20220918143644176

双向链表：两个指针域，分别指向直接前趋和直接后继。在单链表中已知一个结点，求PriorNode的时间复杂度是O(n)，求NextNode的时间复杂度是O(1)。双向链表很好的克服了这个缺点，PriorNode和NextNode时间复杂度都是O(1)。

image-20220918143659724

3.2 带头或者不带头：

带头链表：

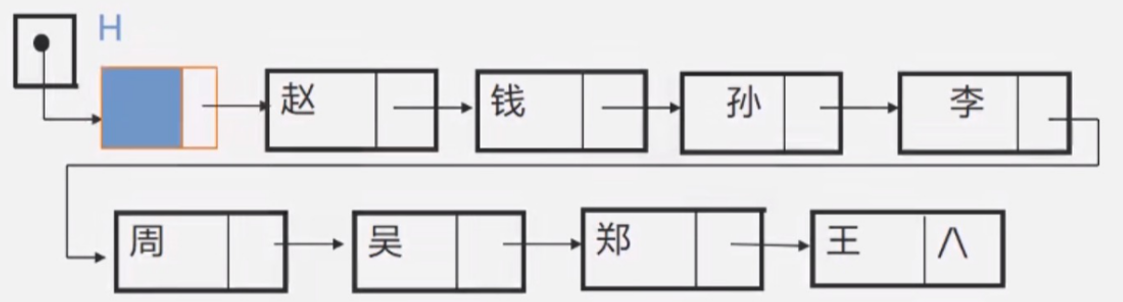
image-20220918144155430

不带头链表：（带头指针的链表不需要用到二级指针）

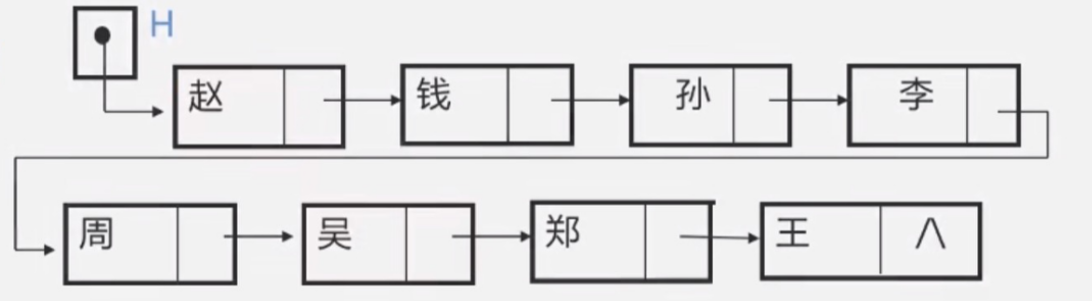
image-20220918144130856

3.3 循环或者非循环：

循环链表：（尾结点指针指向头节点，形成环）

image-20220918142741282

非循环链表：（尾结点指向NULL）

image-20220918142511993

  1. 无头单向非循环链表：结构简单，一般不会单独用来存数据。实际中更多是作为其他数据结构的子结构，如哈希、图的邻接表等等。

  2. 带头双向循环链表：结构最复杂，一般用在单独存储数据。实际中使用的链表数据结构，都是带头双向循环链表。另外这个结构虽然结构复杂，但是使用代码实现以后会发现结构会带来很多优势，代码实现变简单了。

  1. 链表结点：

    链表的结点通常由数据域和指针域组成，数据域存储数据，指针域存储指针，表示结点之间的逻辑关系。

  2. 术语：

    首元结点：指链表中存储第一个数据元素的结点

    头节点：是在链表的首元结点之前附设的一个结点，其数据域可以不存信息，也可以存储诸如线性表长度之类的附加信息。指针域存储首元结点的地址。

    头指针：指向链表中第一个结点的指针。如果该链表有头节点，那么头指针指向头节点。如果该链表没有头节点，头指针指向首元结点。

  3. 链表表示：用结点类型的指针指向链表

4. 不带头单向非循环链表

4.1 结构及特点

  1. 不带头单向非循环链表结构：
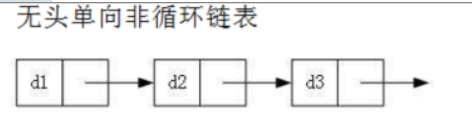
image-20220719222743123

单向链表由结点（结构体）组成，结构体有数据域和指针域，数据域存储数据，指针域是一个指向结构体类型的指针，起到链接每个结点的作用。

  1. 单向链表缺点：找不到前驱，只能从前往后读取信息！要对某个结点操作，必须找到他的前一个结点！所以尾插函数PushBack，尾删函数PopBack，插入元素函数Insert，删除元素函数Erase的时间复杂度都是O(N)。单向不带头非循环链表的主要接口函数有：打印数据，尾插，头插，尾删，头删，查找指定元素，插入元素，删除元素等等。

无头单向非循环链表的结点定义：

（其实只要是单向链表其结点定义均一致，只是不同的操作罢了）

typedef int SLTDataType;
//更改typedef使结构体中Data类型改变（提高数组灵活性和可维护性-平台无关性）
typedef struct SListNode//单向链表的节点
{
	SLTDataType Data;
	SListNode* next;
	//定义一个指向下一个结构体的指针，起串联的作用
	//结构体中不能再次定义结构体（套娃），但可以有指针
}SLTNode;
//为了C中少写struct，在C++中没有必要

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10

无头单向非循环链表主要函数物理结构（代码实现原理）：

  • 删除指定位置元素（逻辑关系映射）：

    image-20220918115741762

  • 第i个位置前插入元素（逻辑关系映射）：

    image-20220918115749971

不难看出，插入删除操作的时间复杂度都是O(n)，因为无论是在第i个位置前插入结点，还是删除第i个位置的结点，都要先遍历，找到第i-1个结点。

以下是标准的单向链表的头文件和源文件（备注有详细解释）单向链的易错点和难点，在本部分结尾处有总结

4.2 单向链表代码实现

  • SList.h头文件
#pragma once
#include<iostream>
using namespace std; 
typedef int SLTDataType;
//更改typedef使结构体中Data类型改变（提高数组灵活性和可维护性-平台无关性）
typedef struct SListNode//单向链表的节点
{
	SLTDataType Data;
	SListNode* next;
	//定义一个指向下一个结构体的指针，起串联的作用
	//结构体中不能再次定义结构体（套娃），但可以有指针
}SLTNode;
//为了C中少写struct，在C++中没有必要

void SListPrint(SLTNode* phead);//打印

//void SListPushBack(SLTNode* phead, SLTDataType x)//传值尾插是标准错误
void SListPushBack(SLTNode** pphead, SLTDataType x);//尾插
//也可以用void SListPushBack(SLTNode*& phead, SLTDataType x)；//最好用

void SListPushFront(SLTNode** pphead,SLTDataType x);//头插
//这里需要改变头指针，所以要传二级指针

void SListPopBack(SLTNode **pphead);//尾删
//如果是只有一个节点需要释放*pphead，要改变头指针，传二级指针

void SListPopFront(SLTNode **pphead);//头删
//需要改变头指针，用二级指针

SLTNode* SListFind(SLTNode* phead,SLTDataType x);//在链表中查找x元素
//不用改变头指针，用一级指针

void SListInsert(SLTNode** pphead, SLTNode* pos, SLTDataType x);//插入元素
//在pos前面插入x，pos通常是函数查找链表数据返回的地址

void SListErase(SLTNode** pphead, SLTNode* pos);//删除pos位置元素
//pos通常是函数查找链表数据返回的地址

//void SListInsert(SLTNode* phead, int i, SLTDataType x);//插入元素，在i位置前插入x（i是下标）不太规范的写法
//void SListErase(SLTNode* phead,int i);//删除i位置的元素（i是下标）不太规范的写法

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • SList.cpp源文件

（注意想要在链表中存储数据，必须是要一节点的形式存储进去，所以在写链表的时候都会包装一个函数：实现将x包装成结点并返回结点地址的函数，如下第一个函数）

#include"SList.h"
SLTNode* BuySLTNode(SLTDataType x)//构造节点的函数（包装）
{
	SLTNode* newnode = (SLTNode*)malloc(sizeof(SLTNode));
	//首先开辟空间存储数据
	newnode->next = NULL;
	newnode->Data = x;//建立相应的节点
	return newnode;
}

void SListPrint(SLTNode* phead)//打印链表数据
{
	SLTNode* cur = phead;
	//cur是当前位置的英文（见名思意）将头地址给cur，此时cur指向第一个节点
	while (cur != NULL)//当cur==NULL的时，即为最后一个节点，停止打印
	{
		cout << cur->Data << "->";
		cur = cur->next;
		//cur->next为下个节点的首地址，cur=cur->next执行后，cur指向下一个节点的首地址
	}cout << "NULL" << endl;
}

//void SListPushBack(SLTNode* phead, SLTDataType x)//传值尾插标准错
void SListPushBack(SLTNode** pphead, SLTDataType x)	//尾插
//也可以用void SListPushBack(SLTNode*& phead, SLTDataType x)；最好用
{
	SLTNode* newnode = BuySLTNode(x);//调用函数构造节点，返回首地址
	if (*pphead == NULL)
	{
		*pphead = newnode;
	}
	else
	{
		SLTNode* tail = *pphead;//tail是尾部的意思
		while (tail->next != NULL)//这里容易写成（tail!=NULL）
		{
			tail = tail->next;
		}//在最后一个节点停止，出循环后tail是最后节点的首地址（尾节点的next==NULL）
		tail->next = newnode;
		//newnode链接在表尾
	}
}

void SListPushFront(SLTNode** pphead, SLTDataType x)//头插,要么传二级指针，要么传指针引用
{
	SLTNode* newnode = BuySLTNode(x);//调用函数构造节点，返回首地址
	newnode->next = *pphead;
	*pphead = newnode;
}

void SListPopBack(SLTNode** pphead)//尾删
{
	//如果链表有没有或者只有一个节点要特别考虑
	if (*pphead == NULL)
	{
		return;
	}
	else if ((*pphead)->next == NULL)
	{
		free(*pphead);
		*pphead = NULL;
	}
	else
	{
		//用两个指针找到最后一个节点的前一个节点（双指针的玩法）
		SLTNode* prev = NULL;
		SLTNode* tail = *pphead;
		while (tail->next != NULL)
		{
			prev = tail;
			tail = tail->next;
		}
		free(tail);
		prev->next = NULL;
	}
}

void SListPopFront(SLTNode** pphead)//头删
{
	SLTNode* next = (*pphead)->next;
	//释放之前需要保存地址，否则整个链表全部丢失！
	//*和->都是解引用的意思，优先及相同需要加上括号，否组可能会报错
	//*解就是对不同类型解引用（取不同的字节数）
	free(*pphead);
	*pphead = next;
	//头指针指向下一个节点的首地址
}

SLTNode* SListFind(SLTNode* phead, SLTDataType x)//在链表中查找x元素
{
	SLTNode* cur = phead;
	while (cur) //cur非空即为真（简洁）
	{
		if (cur->Data == x)
		{
			return cur;
		}
		cur = cur->next;//但其实如果链表中有多个x会出现问题
	}
	return NULL;
    //没找到返回空
}

void SListInsert(SLTNode** pphead, SLTNode* pos, SLTDataType x)//插入元素
//在pos前面插入x，pos通常是函数查找链表数据返回的地址
{
	//如过pos刚好是首地址，相当于头插，要特殊考虑
	if (pos == *pphead)
	{
		SListPushFront(pphead, x);
	}
	else
	{
		SLTNode* prev = *pphead;
        //用一个指针变量保存头指针的值，切记不能直接对头指针操作，会改变头指针！
		while (prev->next != pos)
		{
			prev = prev->next;
		}
		SLTNode* newnode = BuySLTNode(x);
		prev->next = newnode;
		newnode->next = pos;
	}
}

void SListErase(SLTNode** pphead, SLTNode* pos)//删除pos位置元素
//pos通常是函数查找链表数据返回的地址
{
	//如过pos刚好是首地址，相当于头插，要特别考虑
	if (pos == *pphead)
	{
		SListPopFront(pphead);
	}
	else
	{
		SLTNode* prev = *pphead;
		while (prev->next != pos)
		{
			prev = prev->next;
		}
		prev->next = pos->next;
		free(pos);
	}
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88
  • 89
  • 90
  • 91
  • 92
  • 93
  • 94
  • 95
  • 96
  • 97
  • 98
  • 99
  • 100
  • 101
  • 102
  • 103
  • 104
  • 105
  • 106
  • 107
  • 108
  • 109
  • 110
  • 111
  • 112
  • 113
  • 114
  • 115
  • 116
  • 117
  • 118
  • 119
  • 120
  • 121
  • 122
  • 123
  • 124
  • 125
  • 126
  • 127
  • 128
  • 129
  • 130
  • 131
  • 132
  • 133
  • 134
  • 135
  • 136
  • 137
  • 138
  • 139
  • 140
  • 141
  • 142
  • 143
  • 144
  • mian函数测试
#include"SList.h"
void TestSList1()
{
	SLTNode* plist = NULL;
	//定义一个头指针，指向第一个节点
	//指针名字可以是plist或者phead(见名思意)
	SListPushBack(&plist, 11);
	SListPushBack(&plist, 22);
	SListPushBack(&plist, 33);
	SListPushBack(&plist, 44);
	SListPushBack(&plist, 55);//尾插测试
	SListPrint(plist);//打印
	SListPushFront(&plist, 11);
	SListPushFront(&plist, 22);
	SListPushFront(&plist, 33);
	SListPushFront(&plist, 44);
	SListPushFront(&plist, 55);//头插测试
	SListPrint(plist);//打印
	SListPopFront(&plist);//头删测试
	SListPrint(plist);//打印
	SListPopBack(&plist);//尾删测试
	SListPrint(plist);//打印
	SLTNode* pos=SListFind(plist, 33);//查找元素测试
	if (pos)//找到就改为999
	{
		SListInsert(&plist, pos, 999);
	}
	else
	{
		return;

	}
	SListPrint(plist);//打印
}
int main()
{
	TestSList1();
	return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39

结果如下：

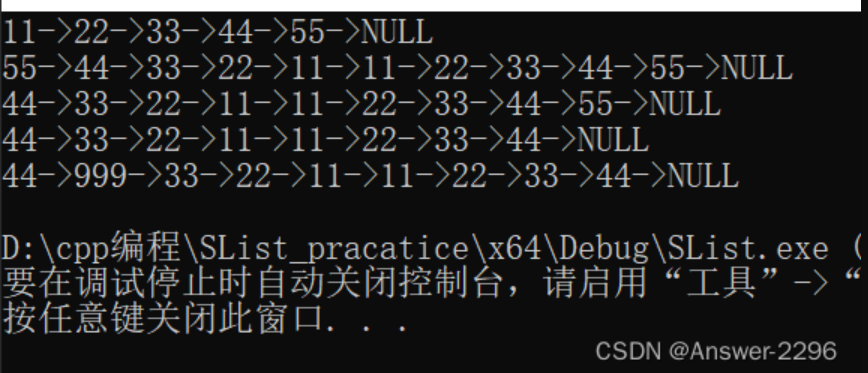
image-20220522160201819

4.3 易错点和重点总结

  1. 二级指针的使用：在头插，尾插，头删，尾删功能的函数实现上出现修改头指针的情况。这时的指针不能传值！（如：void SListPushBack(SLTNode* phead, SLTDataType x)；//尾插函数错误写法），传值传递的是副本，不会改变原来的指针。所以我么会用传地址或引用，如下：

    • void SListPushBack(SLTNode* pphead, SLTDataType x)；*//传地

    • void SListPushBack(SLTNode*& phead, SLTDataType x)；//传引用

    引用很好理解，引用即是别名，别名就是本身。这里解释传地址的方式：传地址由于传是指针的地址，所以用到了二级指针，为了方便理解，如下示图：pphead是指针变量的地址，pphead是pphead地址解引用一次，也就是指针值本身，而pphead里面存放的是结构体的地址，可通过*pphead访问结构体。

    image-20220522160252349

  2. 尾插：尾插函数在定义的时候需要考虑链表空表的情况，否则会bug（会看函数体自行体悟）尾删：需要考虑到空链表和指头一个链表的情况，否则会bug（会看函数体自行体悟）此外删除pos位置元素的函数和在pos（节点地址）前插入元素的函数都需要考虑pos是第一个节点的情况。当然这些问题时建立在上文的函数实现上的，不同函数实现注意点不同。最重要实现函数的时候需要考虑到特殊情况是否满足要求———即空链表是否满足？

  3. 可以发现尾插、头插、中间插函数实现，在参数传递方面没有直接传要插入的结点地址，传的是结点数据域内的数据，通过数据创建新的结点，将新的结点链接到链表中。这是有讲究的。当然函数实现参数传递可以直接传进来待插入结点的地址，插入时使用原来的存储空间固然好，但是当传进来的结点地址不是单独的结点，而是一个链表上的单个结点，这时候对该结点的操作很有可能会损毁链表。如果题目要求使用原来的存储空间，那就得具体题目具体分析了

  4. SLTNode* next = (*pphead)->next;
    *和->都是解引用的意思，优先及相同需要加上括号，否组会报错

5. 带头双向循环链表（List）：

5.1 结构及特点

  1. 带头双向循环链表结构及作用：

双向带头循环链表设计虽然复杂，但是功能实现很简单。双向链表区别域单向链表，循环终止条件由p->next == NULL转变为p->next == head(设置头指针的链表（如上图）)或p ==tail(设置尾指针的链表（如下图）)

image-20220918143335954

  1. 带头双向循环链表概述：

带头双向循环链表是由结点组成，第一个称为哨兵位的头节点head，（哨兵位其实是为了方便操作而引入的结点，不存储有效数据，在很多时候,我们处理某个节点需要用到它的前驱节点，比如删除链表的某个节点,对于没有哨兵的单链表，当待删除的节点为链表的第一个节点,，由于没有前驱,需要进行特殊处理.从而代码的复杂性增加.而如有哨兵节点,则第一个节点的处理方式与其他节点相同,可以统一进行处理。）带头双向循环链表后续就是由结点组成，结点中由有效数据成员和两个指向自身类型的结构体指针，两个指针分别叫做结点的前驱和后继，分别指向上一个结点和下一个结点。每个结点都是一前一后链接在链表上的，下面是结点的定义：

typedef int LTDataType;//提高维护性和平台无关性
struct ListNode
{
	ListNode* next;//后继，指向后一个指针
	ListNode* prev;//前驱，指向前一个结点
	LTDataType Data;//存储有效数据成员
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7

本部分思路为：先弄清楚带头双向循环链表的实现，接着介绍如何在10分钟内完整实现带头双向循环链表，老规矩！链表的增删查改功能请看头文件和源文件！代码精华会在后面详细解答！

5.2 主要操作及实现原理

  1. 插入数据

  • 将数据包装成结点

  • 链接到双向链表，由于是双向循环链表，会修改四个指针，分别是新节点和直接前趋和直接后继的指针链接，如下：

    image-20221011162023171

    但具体如果是头插问题可能会修改到双向链表的头指针，则需具体考虑

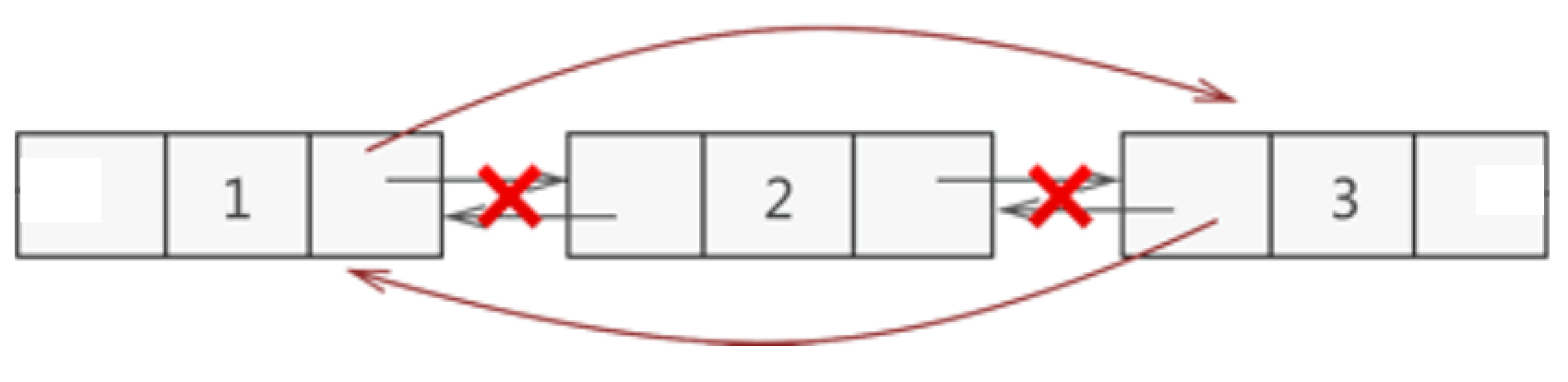
  1. 删除结点

  • 用指针存储目标删除结点

  • 将数据元素的直接前趋和直接后继链接起来。

  • 释放删除结点占用的内存空间。

image-20221011162618806

5.3 双向链表的代码实现

  • List.h头文件
#pragma once
#include<iostream>
#include<assert.h>
using namespace std;
typedef int LTDataType;//提高维护性和平台无关性
struct ListNode
{
	ListNode* next;//后继，指向后一个指针
	ListNode* prev;//前驱，指向前一个结点
	LTDataType Data;//存储有效数据成员
};
void ListInit(ListNode*& phead);//初始化

void ListPrint(ListNode*phead);//打印链表

void ListDestory(ListNode* phead);//消除数据

void ListPushBack(ListNode* phead, LTDataType x);//尾插

void ListPushFront(ListNode* phead, LTDataType x);//头插

void ListPopBack(ListNode* phead);//尾删

void ListPopFront(ListNode* phead);//头删

ListNode* ListFind(ListNode* phead, LTDataType x);//查找存有x的结点，并返回该节点地址

void ListInsert(ListNode* pos, LTDataType x);
//在pos位置前插入存有x的结点,pos一般是ListFind函数查找返回的地址

void ListErase(ListNode* pos);
//删除pos位置的结点，pos一般是ListFind函数查找返回的地址

bool ListEmpty(ListNode* phead);//判断空
int ListSize(ListNode* phead);//判断大小

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • List.cpp源文件

（注意想要在链表中存储数据，必须是要一节点的形式存储进去，所以在写链表的时候都会包装一个函数：实现将x包装成结点并返回结点地址的函数，如下第一个函数）

#include"List.h"
ListNode* BuyListNode(LTDataType x) //创造结点功能的函数包装
{
	ListNode* newnode = (ListNode*)malloc(sizeof(ListNode));
	newnode->Data = x;
	newnode->next = NULL;
	newnode->prev = NULL;
	return newnode;
}

void ListInit(ListNode*& phead)//初始化,改变指针用指针和引用均可，此处用引用
{
	phead = BuyListNode(0);//head哨兵位头节点，不存有效数据
	phead->next = phead;
	phead->prev = phead;
	//head哨兵位指针都是自己指向自己，很完美的设计，后面详解
}

void ListPrint(ListNode* phead)//打印链表
{
	assert(phead);//排除空指针闯传入
	ListNode* cur = phead->next;
	while (cur != phead)
	{
		//当cur=phead时说明刚好遍历一次或者该链表没有数据
		cout << cur->Data << " ";
		cur = cur->next;
	}
	cout << endl;
}

void ListIniDestory(ListNode* phead)//消除数据
{
	assert(phead);//排除空指针闯传入
	ListNode* cur = phead->next;
	while (cur != phead)
	{
		ListNode* next = cur->next;
		free(cur);
		cur = next;
	}//要每个指针都释放，而不是不负责的只释放phead
	free(phead);
	phead = NULL;
}

void ListPushBack(ListNode* phead, LTDataType x)//尾插
{
	//循环链表中哨兵位的prev指针指向的就是尾结点！
	assert(phead);//排除空指针闯传入
	ListNode* tail = phead->prev;//tail就是尾结点地址
	ListNode* newnode = BuyListNode(x);//将x包装成结点
	//三个结点之间链接！phead newnode tail
	tail->next = newnode;
	newnode->prev = tail;
	newnode->next = phead;
	phead->prev = newnode;
}

void ListPushFront(ListNode* phead, LTDataType x)//头插
{
	assert(phead);//排除空指针闯传入
	ListNode* newnode = BuyListNode(x);//将x包装成结点
	ListNode* first = phead->next;//first就是第一个结点地址
	//三个结点之间链接！phead,first,newnode
	phead->next = newnode;
	newnode->prev = phead;
	newnode->next = first;
	first->prev = newnode;
}

void ListPopBack(ListNode* phead)//尾删
{
	assert(phead);//排除空指针闯传入
	assert(phead->next != phead);//只有哨兵位头节点不能删
	ListNode* tail = phead->prev;//tail就是尾结点地址
	ListNode* prev = tail->prev;//prev是倒数第二个结点的地址
	prev->next = phead;
	phead->prev = prev;
	free(tail);
	tail = NULL;//别忘了释放指针并置空
}

void ListPopFront(ListNode* phead)//头删
{
	assert(phead);//排除空指针闯传入
	assert(phead->next != phead);//只有哨兵位头节点不能删
	ListNode* first = phead->next;//first就是第一个结点地址
	ListNode* second = first->next;//second就是第二个结点地址
	phead->next = second;
	second->prev = phead;
	free(first);
	first = NULL;//别忘了释放指针并置空
}

ListNode* ListFind(ListNode* phead, LTDataType x)//查找存x的结点,返回该结点的地址
{   //ListFind函数是可以修改结点有效数据的，对函数返回值解引用"->"可修改特定位置的数值
	assert(phead);//排除空指针闯传入
	ListNode* cur = phead->next;
	while (cur != phead)//cur=phead就遍历一次或者链表为空链表
	{
		if (cur->Data == x)
		{
			return cur;//找到x的结点返回结点地址
		}
		cur = cur->next;
	}return NULL;
}

//在pos位置前插入存有x的结点,pos一般是ListFind函数查找返回的地址
void ListInsert(ListNode* pos, LTDataType x)
{
	assert(pos);//排除空指针闯传入
	ListNode* prev = pos->prev;
	ListNode* newnode = BuyListNode(x);
	//三个结点之间链接！prev newnode pos
	prev->next = newnode;
	newnode->prev = prev;
	newnode->next = pos;
	pos->prev = newnode;
}

//删除pos位置的结点，pos一般是ListFind函数查找返回的地址
void ListErase(ListNode* pos)
{
	assert(pos);//排除空指针闯传入
	ListNode* prev = pos->prev;
	ListNode* next = pos->next;
	//找到pos的前一个prev，和后一个next，链接next和prev释放free
	prev->next = next;
	next->prev = prev;
	free(pos);
	pos = NULL;
}

bool ListEmpty(ListNode* phead)//判断空 空返回1，非空返回零
{
	assert(phead);
	return phead->next == phead;
}

int ListSize(ListNode* phead)//判断大小
{
	assert(phead);
	int Size = 0;
	ListNode* cur = phead;
	do
	{
		Size++;
		cur = cur->next;
	} while (cur != phead);
	return Size;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88
  • 89
  • 90
  • 91
  • 92
  • 93
  • 94
  • 95
  • 96
  • 97
  • 98
  • 99
  • 100
  • 101
  • 102
  • 103
  • 104
  • 105
  • 106
  • 107
  • 108
  • 109
  • 110
  • 111
  • 112
  • 113
  • 114
  • 115
  • 116
  • 117
  • 118
  • 119
  • 120
  • 121
  • 122
  • 123
  • 124
  • 125
  • 126
  • 127
  • 128
  • 129
  • 130
  • 131
  • 132
  • 133
  • 134
  • 135
  • 136
  • 137
  • 138
  • 139
  • 140
  • 141
  • 142
  • 143
  • 144
  • 145
  • 146
  • 147
  • 148
  • 149
  • 150
  • 151
  • 152
  • main函数测试
#include"List.h"
void ListTest()
{
	ListNode* A;
	ListInit(A);
	/*ListNode B;
	ListInit(&B);*/错误写法！
	ListPushBack(A, 1);
	ListPushBack(A, 2);
	ListPushBack(A, 3);//尾插测试
	ListPrint(A);
	ListPushFront(A, -1);
	ListPushFront(A, -2);
	ListPushFront(A, -3);//头插测试
	ListPrint(A);
	ListPopBack(A);//尾删测试
	ListPrint(A);
	ListPopFront(A);//头删测试
	ListPrint(A);
	ListNode* tmp = ListFind(A, 1);//查找元素测试
	ListInsert(tmp,666);//插入元素测试
	ListErase(tmp->next);//删除元素测试
	cout << "List NULL or not ?(NULL:1,not NULL:0) =" << ListEmpty(A) << endl;
	cout << "there is " << ListSize(A) << " nodes in the List" << endl;
}
int main()
{
	ListTest();
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29

结果：image-20220522155219457

5.4 精华和细节

  1. 一分钟之内完整实现带头双向循环链表：不难发现所谓头删，尾删，头插，尾插其实不过是最后两个再pos位置删除插入函数（ListInsert，ListErase）的特殊形式，所以实现带头双向循环链表的头删，尾删，头插，尾插函数只需要写两个再pos位置删除插入函数（ListInsert，ListErase）的函数其余就行啦！看cpp代码！
void ListPushBack(ListNode* phead, LTDataType x)//尾插
{
	assert(phead);//排除空指针闯传入
	ListInsert(phead->prev，x);
}

void ListPushFront(ListNode* phead, LTDataType x)//头插
{
	assert(phead);//排除空指针闯传入
	ListInsert(phead->next,x);
}

void ListPopBack(ListNode* phead)//尾删
{
	assert(phead);//排除空指针闯传入
	ListErase(phead->prev);
}

void ListPopFront(ListNode* phead)//头删
{
	assert(phead);//排除空指针闯传入
	ListErase(phead)一句化搞定上面所有，当然还是要断言以下的
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  1. 带头双向循环链表的结构完美性：任意位置都可以删除插入都是O(1),但查找还是O(N)。以后查找会用平衡搜索树（AVL树和红黑树），哈希表，B树，B+树系列，跳表，布隆过滤器，位图等。此外会发现在无头单向非循环链表中，头插尾插头删尾删等函数需要考虑链表的特殊情况，如链表只有一个结点或者空链表的情况都需要单独考虑，但在带头双向循环链表中是不需要考虑的（不信回试），**带头双向循环链表的代码实现满足一般情况也能满足特殊情况！**所以写代码的时候只需要按下面这个结构写：
image-20220522160524939
  1. 头插，尾插的代码实现最好的思路是，找到插入的结点newnode和前一个结点prev和后一个结点next，然后再对这三个结点newnode，prev，next进行链接，这样的链接方式不需要考虑链接顺序，思路清晰不会出错。直接插入的方式代码简单一丢丢，需要注意链接顺序，必须先链接后面再链接前面，否则会出现修改了前面的指针找不到后面的指针的情况，以头插为例子：
//正确写法：
void ListPushFront(ListNode* phead, LTDataType x)//头插
{
	assert(phead);//排除空指针闯传入
	ListNode* newnode = BuyListNode(x);//将x包装成结点
    newnode->next=phead->next;//先把后面链接
	phead->next->prev = newnode;//先把后面链接
	phead->next = newnode;//再链接前面
	newnode->prev = phead;//再链接前面
}

//错误写法：
void ListPushFront(ListNode* phead, LTDataType x)//头插
{
	assert(phead);//排除空指针闯传入
	ListNode* newnode = BuyListNode(x);//将x包装成结点
	phead->next = newnode;//先链接了前面
	newnode->prev = phead;//先链接了前面
    newnode->next=phead->next;//此处出现问题phead->next就是newnode本身！
	phead->next->prev = newnode;//phead->next->prev是phead
     //可以发现已经乱套了！
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  1. 哨兵位头节点中的哨兵位的头节点一定不要存有效数据！存了会在某些类型问题上出现问题：
typedef int LTDataType;
struct ListNode
{
	ListNode* next;
	LTDataType Data;
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6

不少人希望通过再哨兵位数据中存储数组中元素个数来达到遍历的方便，但在一些情况会出现问题，当这里LTDataType是int类型一般没有问题，但LTDataType是char类型的时候，当数组元素超过128时，再插入数据就会出现溢出现象，此外还有其他情况也可能出现问题，就不在此一一列举了。

  1. assert断言的好处，未来在大厂工作，代码少则都时万行，assert的好处在于程序出现问题，会告诉你出发了那个断点，当程序代码多时，告诉你错误的位置好处不言而喻，维护性大大提高。

6. 链表中常见算法

6.1 反转单链表的三种算法

如上，反转链表就是将链表的链接顺序，从尾链接到头，具体实现方法有四种：

6.1.1 迭代法反转链表（三指针反转链表）

该算法用到beg，mid，end三个指针。

beg是反转链表的头，开始指向NULL，mid指向原链表的头。

mid指针沿着链表向后遍历，直到空为止。逐个将结点头插到反转链表beg上，而end指针记录mid的下一个结点，供mid向后遍历，具体如下：

原链表：

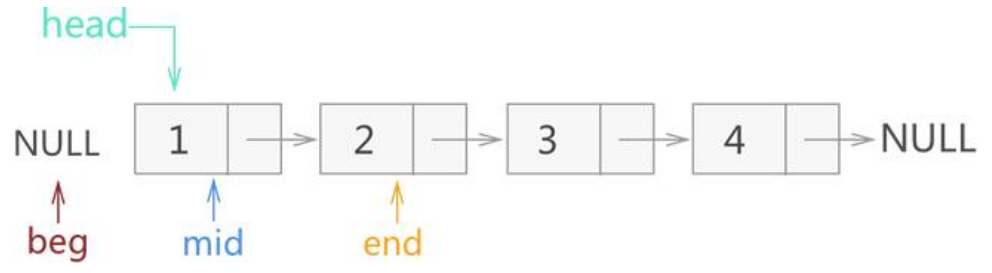
image-20221010235814064

将1号结点头插反转链表中，mid向后遍历：

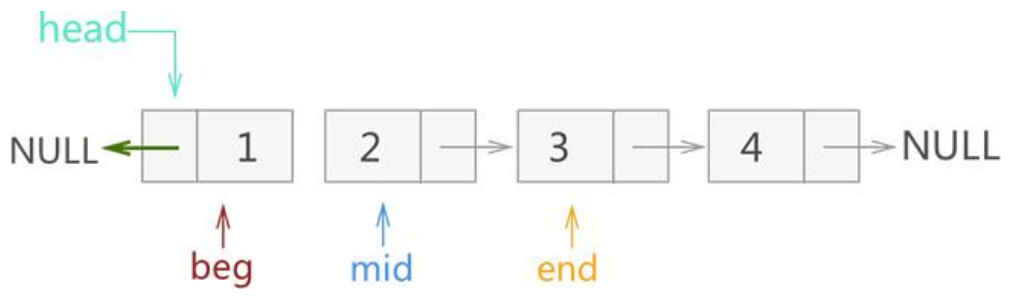
image-20221010235928217

接着将2号结点头插反转链表，mid向后遍历

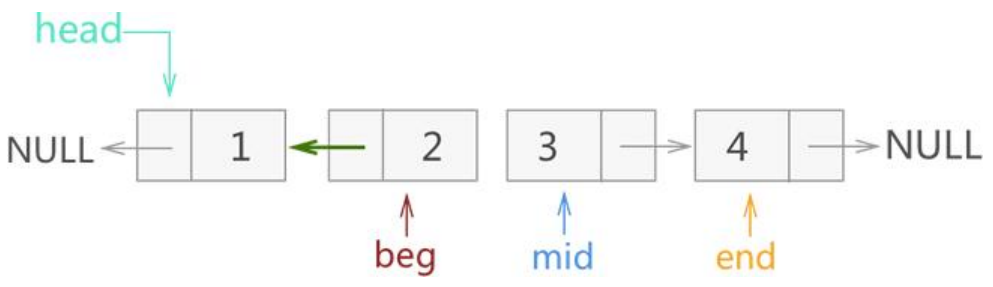
image-20221011000152251

接着将3号结点头插反转链表，mid向后遍历

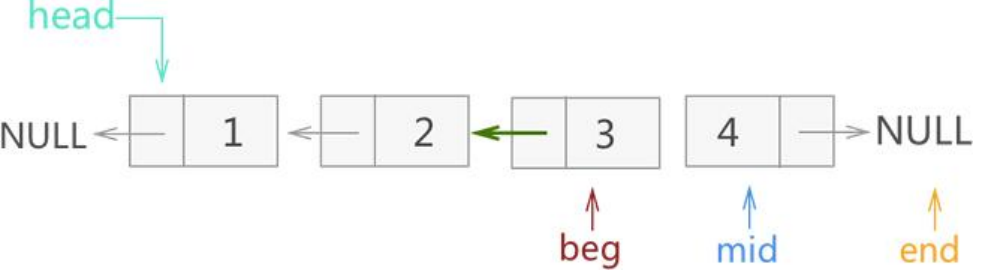
image-20221011000224629

接着将4号结点头插反转链表，mid向后遍历

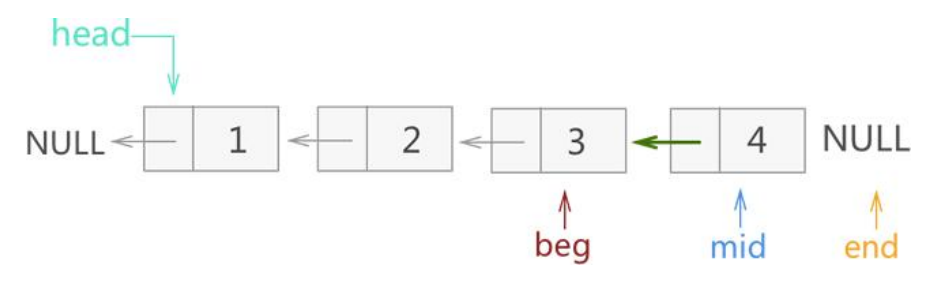
image-20221011000244642

再下一步，mid指向空，循环停止

代码实现：

//该链表是不带头节点的实现
SListNode* reversal(SListNode* s)
{
	if (!s)return s;
	SListNode* beg = NULL, * mid = s, * end = s->next;
	while (mid)
	{
		//头插反转链表
		mid->next = beg;
		beg = mid;
		//mid向后遍历
		mid = end;
		if (end != NULL)end = end->next;//赋值前判断，防止空指针出现
	}
	return beg;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16

6.1.2 递归反转链表

算法思路：从后往前依次链接结点，就实现了链表反转。返回最后结点的地址。这个思路的难点在于从后往前将结点依次链接需要得到每一个结点的地址，才能进行链接操作。但我们使用的单项链表只能从前往后寻址，如果每次寻址都定义变量存储当前接结点的地址，但我们并不知道该链表有多少个结点。

这里使用递归就能很好解决这个问题，因为每一层递归都能很好的记录下当前结点的地址，并且无需关心有多少个结点。

实现概述：用递归查找最后一个节点，而查找的过程，每一层递归栈区都依次记录了当前结点的地址，在当前层递归进行相邻结点的反向链接，依次退出递归，最终实现整个链表的反转。

代码实现：

SListNode* reversal(SListNode* s)
{
	if (s == NULL || s->next == NULL)return s;
	else
	{
		SListNode* newHead = reversal(s->next);
		//循环每次推出newHead均指向原链表的最后一个结点

		
		s->next->next = s;
		s->next = NULL;
		return newHead;
	}
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14

下图简述代码实现过程，沿着绿色箭头就是查找最后一个结点的过程，也是进入递归的过程，沿着蓝色箭头即为退出递归顺序，中间链接反转即为反转相邻两个结点

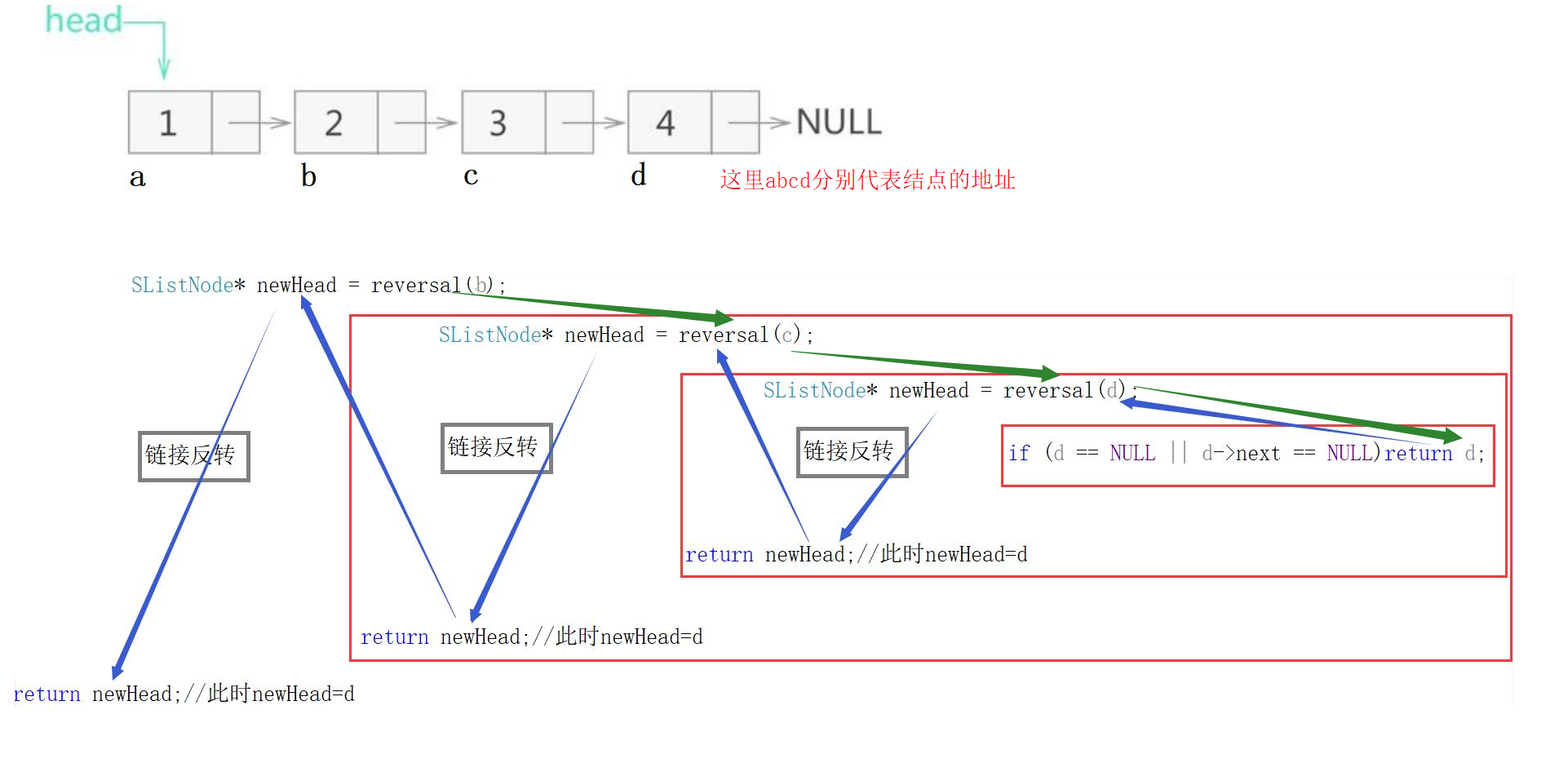
image-20221011134059347

从右向左，链接反转的逻辑，

第一次反转，也就是第三层递归

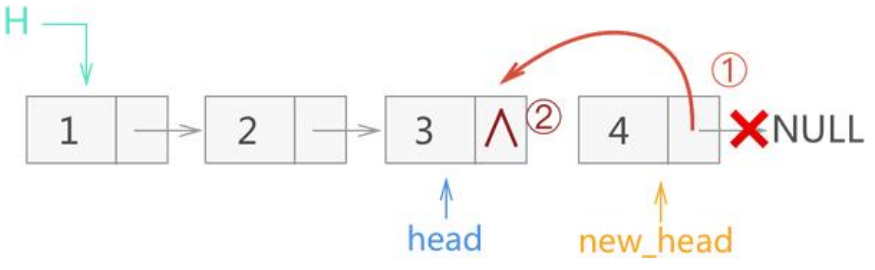
image-20221011133350657

第二次反转，也就是第二层递归

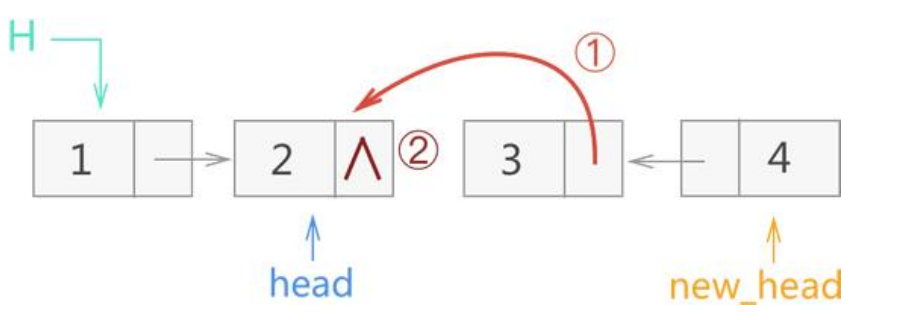
image-20221011133401489

第三次反转，也就是第一层递归

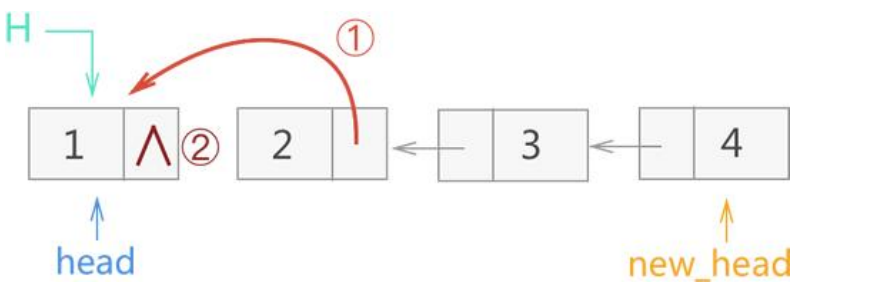
image-20221011133408210

6.1.3 头插法反转链表

算法思路：创建空链表newHead，将原链表每个结点依次头插在newHead链表上，实现头插函数实现前面基础部分有。代码实现简单不在此赘述

逻辑实现过程

  1. 创建空链表newHead

    image-20221011134907091

  2. 从原链表中摘除头部节点 1，并以头部插入的方式将该节点添加到新链表中

    image-20221011134957136

  3. 继续重复以上工作，直到头部节点为空。先后将节点 2、3、4 从原链表中摘除，并以头部插入的方式添加到新链表中

    image-20221011135202981

6.2 单链表是否相交问题

单链表相交问题值得注意的是，单链表只有一个指针域的特性决定了两个链表相交后不可能再再产生分支了。就是说不存在以下情况：

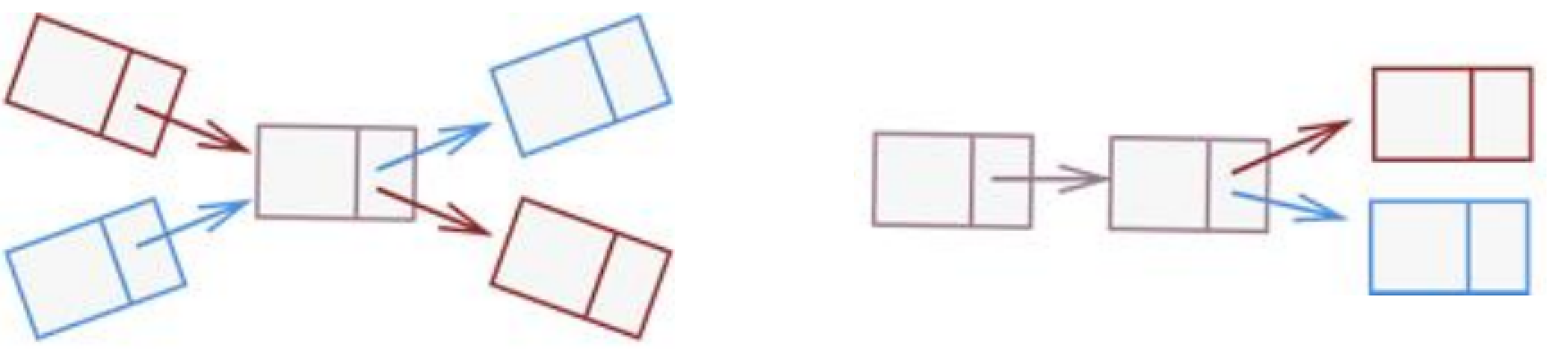
image-20221011150845719

而应该考虑如下情况：

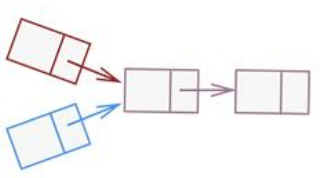
image-20221011150938276

实现方法一：非常的low

用遍历，比对结点的地址是否相同，但凡有一个地址相同，就return true。具体实现很简单，不在此赘述。时间复杂度为
O ( n 2 ) O(n^2) O(n2)

实现方法二：改进

前面说过，两个单链表的若相交，后面就一定不产生分支。所以只需要比对尾结点地址是否相等即可。时间复杂度为
O ( n ) O(n) O(n)

6.3 环形链表——快慢指针问题

141. 环形链表

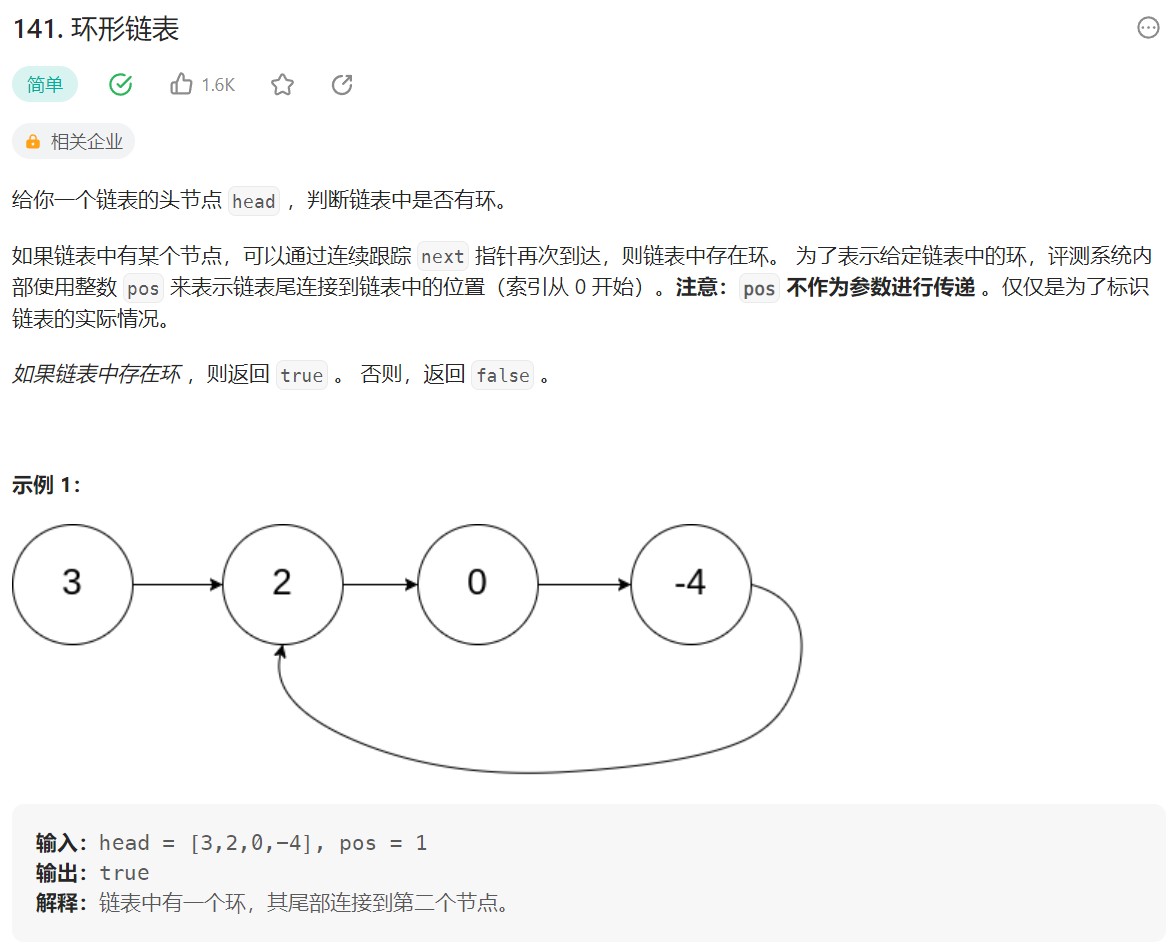
image-20221013234640322

  1. 题解——快慢指针

利用快慢指针在循环中追逐判断循环是否存在。其余的判断是否重复的方法均不可靠！

class Solution {
public:
    bool hasCycle(struct ListNode *head) {
        ListNode* slow = head;
        ListNode* fast = head;
        while(fast && fast->next)
        {
            slow = slow->next;
            fast = fast->next->next;
 
            if(slow == fast)
            return true;
        }
        return false;
}
};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  1. 深入——快慢指针一定能追上吗？

首先结论

  • 快指针和慢指针速度相差1，一定能追上。快指针和慢指针相差非1，就不一定了

对于这个问题我们用相对速度来解释，首先快指针是慢指针的两倍。

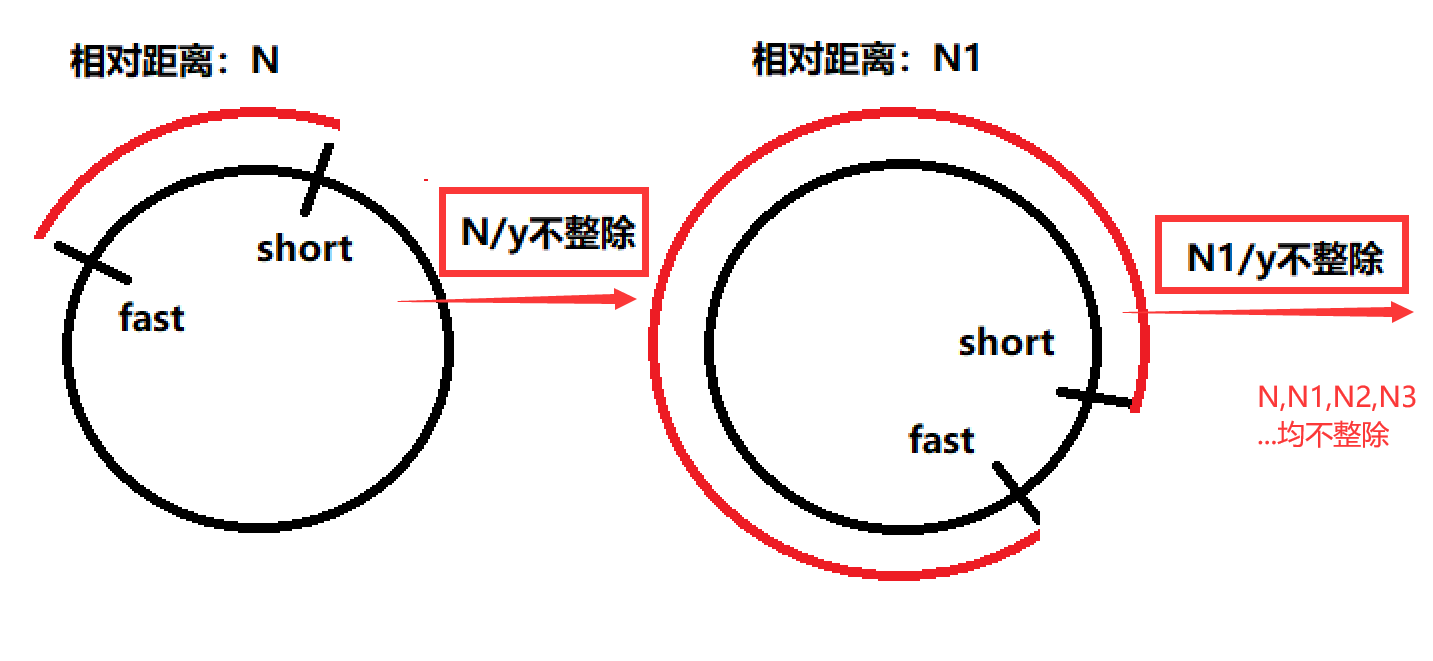
fast=x; slow=x-1;，那么快慢指针相对速度为fast-slow=1。而快慢指针进入循环刚开始开始追逐时，相对距离是N，根据高中物理经过N/1的时间，快慢指针一定会相遇！因为整除了！

但是对于快慢指针速度相差y（y!=1）,的情况相对速度是y，对于任意的初始相对距离N，N/y是未必整除的，不整除就意味着快指针从慢指针身上跳过，但没有相遇。并且沿着循环圈，开始新的一轮追逐，这次初始相对距离可能与上次不同，这里设为N1，如果N1/y任然不整除，那么就再次擦身而过。再次追逐，一次类推N2,N3…如果这些N,N1,N2,N3…都不能整除y，那么就永远也值不上了，懂了吧？（N,N1,N2,N3这些距离可能会出现循环）

image-20220728235056478

7. 顺序表和链表的比对

  • 顺序表优势体现在元素高效存储，频繁访问。缓存利用率高。

  • 链表优势体现在任意位置插入和删除频繁。缓存利用率低

从空间利用率来看

从空间利用率的角度上看，顺序表的空间利用率显然要比链表高。

这是因为，链表在存储数据时，每次只申请一个节点的空间，且空间的位置是随机的，如图 2 所示：

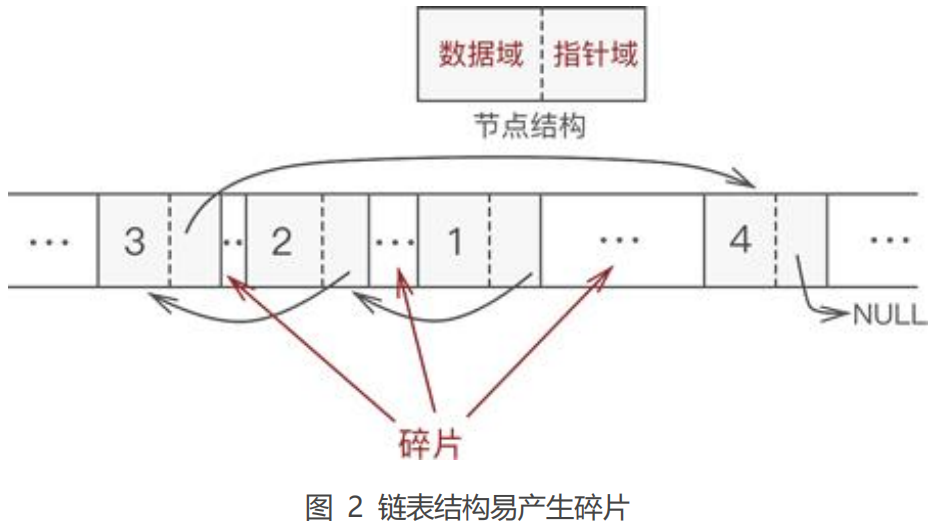
image-20221010102105723

这种申请存储空间的方式会产生很多空间碎片，一定程序上造成了空间浪费。不仅如此，由于链表中每个数据元素都必须携带至少一个指针，因此，链 表对所申请空间的利用率也没有顺序表高。

空间碎片:指的是某些容量很小（1KB 甚至更小）以致无法得到有效利用的物理空间。

从时间复杂度来看

访问数据来看：顺序表继承数组的优势，随机存储，访问任意位置的时间复杂度为O(1)，而在链表中访问数据元素，需要从表头依次遍历，直到找到指定节点，花费的时间复杂度为 O(n);

从插入删除来看：

链表插入或删除节点操作，只需改变相应节点的指针指向即可，无需大量移动元素，因此链表中插入、删除或移动数据所耗费的时间复杂度为 O(1)；而顺序表中，插入、删除和移动数据可能会牵涉 到大量元素的整体移动，因此时间复杂度至少为 O(n);

8. 存储结构和存取结构区别

存储结构，指的是数据在内存中真实的存储状态，具体可分为 2 类，即顺序存储结构和链式存储结构

存取结构，指的是存取数据的方式，具体也可以分为 2 类，分别为顺序存取结构和随机存取结构

线性表按存储结构分为：顺序存储的顺序表和链式存储的链表

顺序表是随机存取结构，按数组下标实现随机的存取数据。

链表是顺序存储结构，访问指定位置结点，只能从链表头开始向后遍历找到指定位置的地址，通过地址对结点数据进行存取。

线性表的顺序存储结构，又可以称为随机存取结构；而线性表的链式存储结构（栈和队列），又可以称为顺序存取结构。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/从前慢现在也慢/article/detail/550673
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号