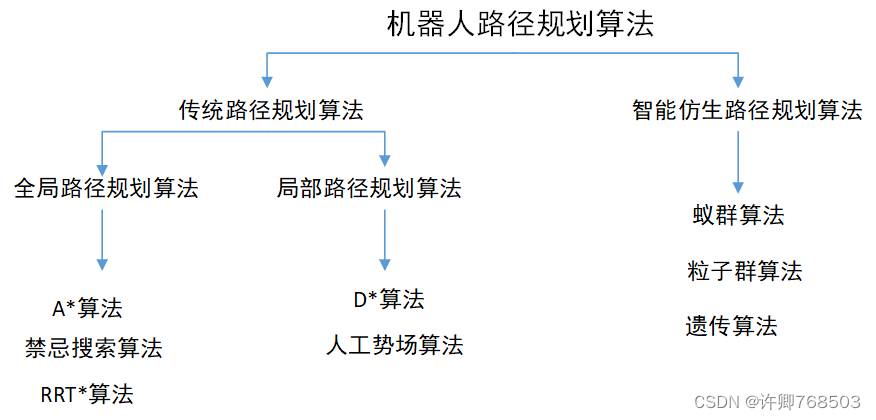
各类路径规划算法大全（一）_局部路径规划算法有哪些

       目前路径规划存在的问题主要为环境建模困难、算法收敛素速度慢、容易陷入局部最优解，此外传统的路径规划算法需要在建立全局地图的基础上进行路径规划，即在已知地图中进行，这种算法导致了感知和决策分离，难以应用到位置环境中，因此后来相关研究者将兴趣放到了智能算法的研究上。

一、全局路径规划算法分类——传统算法

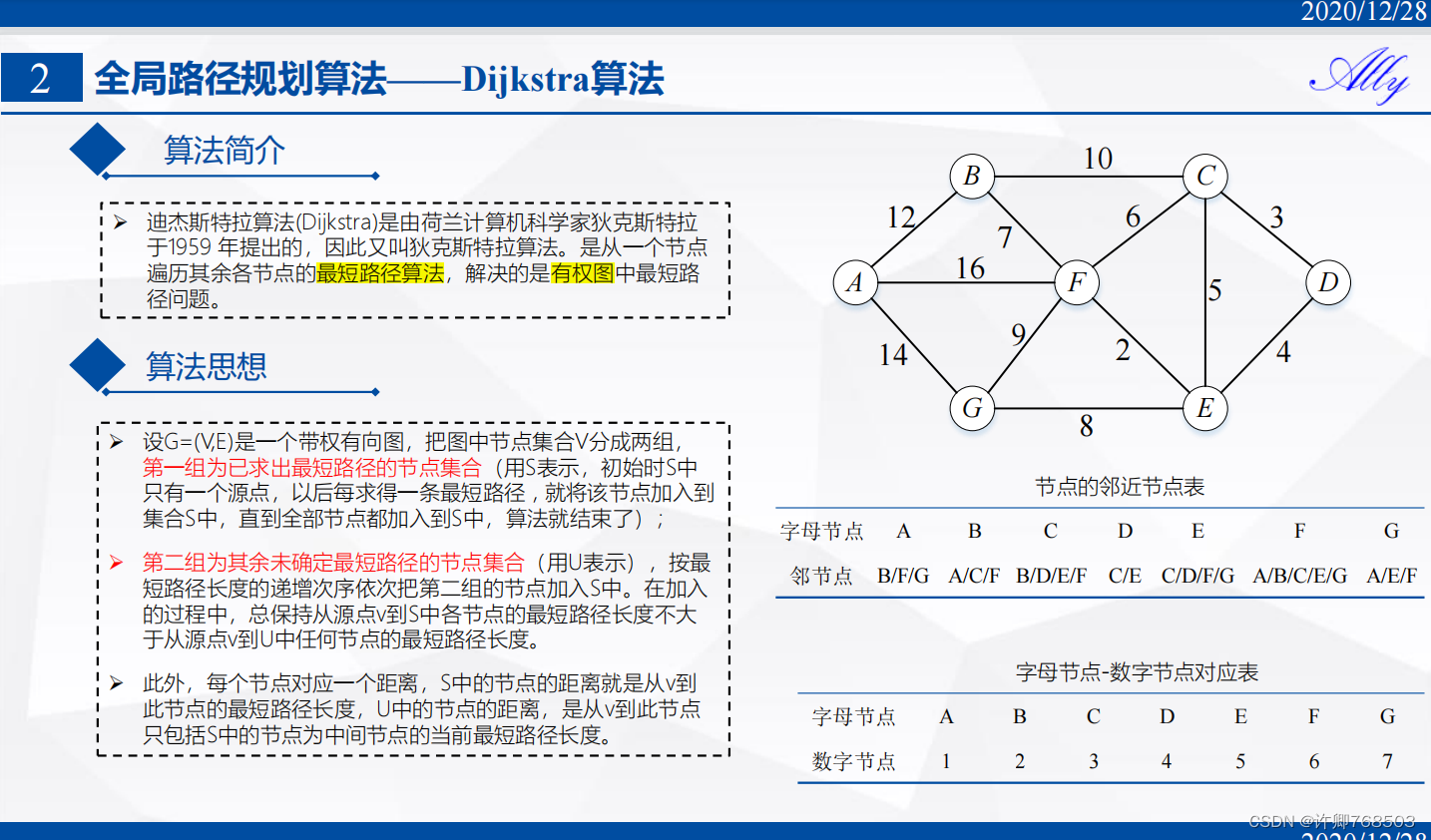
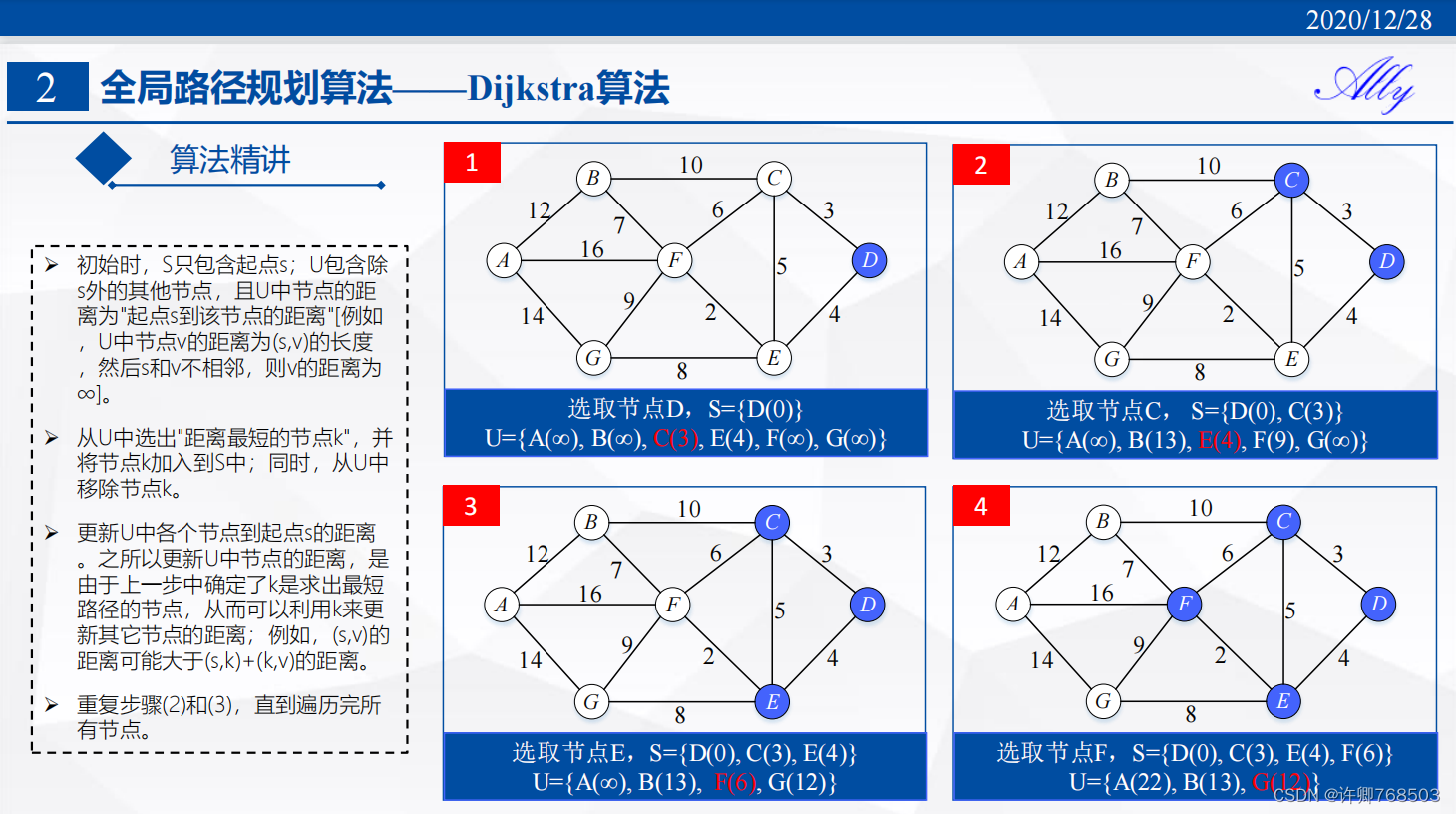
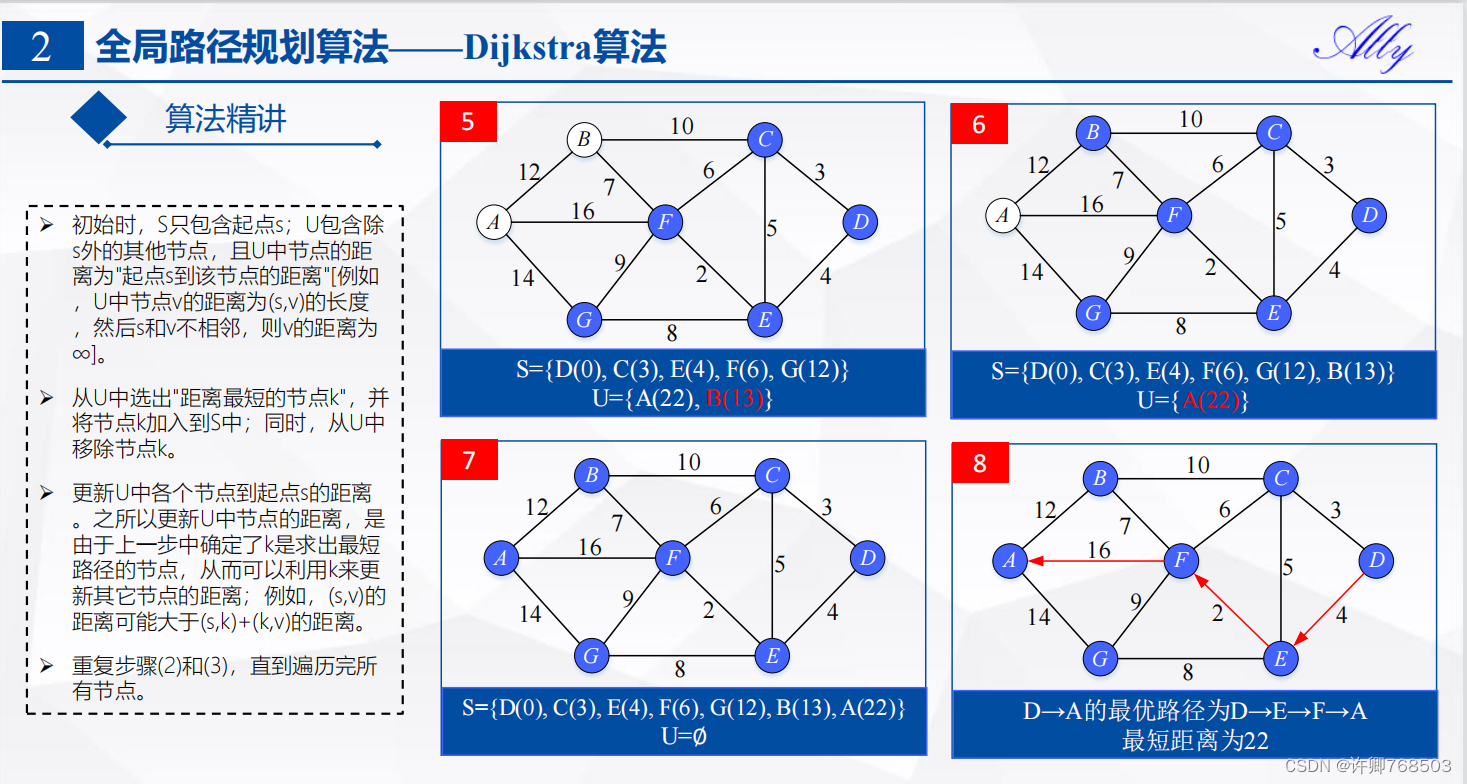
0、Dijkstra算法

• 是最经典的图搜索算法之一，属于广度优先算法，采用遍历的方式，计算起点到终点的所有路径，并选择成本最低的路径，因此可搜索最短路径。
• 广度优先搜索，能获得全局最优路径，耗时较长，遇到障碍物只能重复规划（replan）
• 贪心模式，其解决的是有向图中单个节点到另一节点的最短路径问题
• 静态规划
• 栅格地图

 

1、A*算法

• 启发式搜索算法，以此来衡量实时搜索位置和目标位置的距离关系，使搜索方向优先朝向目标点所处位置的方向，最终达到提高搜索效率的效果。
• 融合了贪心和启发思想，能快速搜索路径，路径并非全局最优，遇到障碍物只能重复规划（replan）
• 静态规划
• 栅格地图

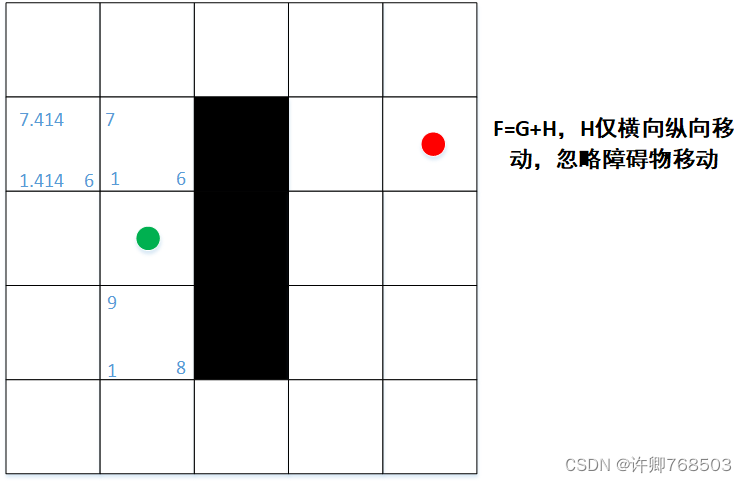
（1）开始搜索

       从起点开始，检查其相邻的方格，然后向四周扩展，直至找到目标。

       <1>. 从起点 A 开始，并把它就加入到一个由方格组成的 open list( 开放列表 ) 中。现在 open list 里只有一项，它就是起点 A ，后面会慢慢加入更多的项。 Open list 里的格子是路径可能会是沿途经过的，也有可能不经过。基本上 open list 是一个待检查的方格列表。

       <2>. 查看与起点 A 相邻的方格 ( 忽略其中墙壁所占领的方格) ，把其中可走的 (walkable) 或可到达的 (reachable) 方格也加入到 open list 中。把起点 A 设置为这些方格的父亲 (parent node 或 parent square) 。

       <3>. 把 A 从 open list 中移除，加入到 close list( 封闭列表 ) 中， close list 中的每个方格都是现在不需要再关注的。如下图所示，深绿色的方格为起点，它的外框是亮蓝色，表示该方格被加入到了 close list 。与它相邻的黑色方格是需要被检查的，他们的外框是亮绿色。每个黑方格都有一个灰色的指针指向他们的父节点，这里是起点 A 。

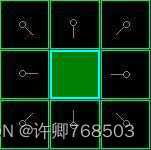
       <4>. 我们需要从 open list 中选一个与起点 A 相邻的方格，按下面描述的一样或多或少的重复前面的步骤。但是到底选择哪个方格好呢？选择具有最小 F 值的那个。

（2）继续搜索

       <5>. 为了继续搜索，我们从 open list 中选择 F 值最小的 ( 方格 ) 节点，然后对所选择的方格作如下操作:

        把它从 open list 里取出，放到 close list 中。

        检查所有与它相邻的方格，忽略其中在 close list 中或是不可走 (unwalkable) 的方格 ，如果方格不在open lsit 中，则把它们加入到 open list 中。把我们选定的方格设置为这些新加入的方格的父亲。

        如果某个相邻的方格已经在 open list 中，则检查这条路径是否更优，也就是说经由当前方格 ( 我们选中的方格 ) 到达那个方格是否具有更小的 G 值。如果没有，不做任何操作。相反，如果 G 值更小，则把那个方格的父亲设为当前方格 ( 我们选中的方格 ) ，然后重新计算那个方格的 F 值和 G 值。

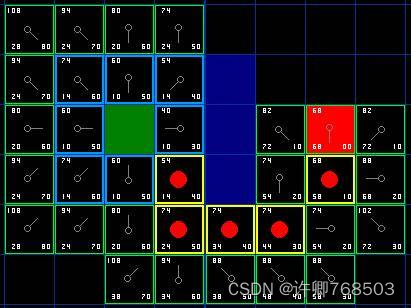
       <6>. 把终点加入到了 open list 中，此时路径已经找到了，或者查找终点失败，并且 open list 是空的，此时没有路径。

（3）优、缺点

其收敛速度比较快，稳定性较高。A*算法是一种启发式搜索算法，将广度优先搜索（BFS）和常规路径规划算法Dijkstra算法相结合。通过利用一个启发函数来改变其搜索性能，从而可以更快的找到路径，并且找到的一定是最短路径。A *算法计算量较大，运行时间较长等问题凸显。A*算法在Dijkstra算法基础之上改进而来。

2、Hybrid A*算法

       考虑到车辆初始方向和终点方向，以及每一次节点拓展都符合车辆的运动学。Hybrid A*规划的路径由两部分组成，第一部分是考虑了车辆运动学的探索结点连接而成的路径；第二部分是使用ReedSheeps曲线连接中间点位姿与目标位姿的路径。

（1）Hybrid A*的结点拓展：x,y方向的拓展，还考虑了Θ方向的探索。结点拓展是三维的。

（2）启发式约束：考虑航向角及其半径。结合车辆运动学约束。

3、RRT*算法

       

        RRT是一种在完全已知的环境中通过随机采样扩展搜索的算法

• 特点：RRT算法是概率完备的，如果规划时间足够长，如果确实存在一条可行的最优路径，RRT是可以找出这条路径的。但这里存在限制条件，如果规划时间不够长，迭代次数较少，有可能无法找出实际存在的路径。
• 优点：最主要的优点就是快，因此在多自由度机器人的规划问题中发挥着较大的作用，比如机械臂的规划算法基本都是以RRT为基础的。
• 缺点：规划的路径通常不最优、路径不平滑等。

        尽管RRT算法是一个相对高效率，同时可以较好的处理带有非完整约束的路径规划问题的算法，并且在很多方面有很大的优势，但是RRT算法并不能保证所得出的可行路径是相对优化的。因此许多关于RRT算法的改进也致力于解决路径优化的问题，RRT*算法就是其中一个。RRT*算法的主要特征是能快速的找出初始路径，之后随着采样点的增加，不断地进行优化直到找到目标点或者达到设定的最大循环次数。RRT*算法是渐进优化的，也就是随着迭代次数的增加，得出的路径是越来越优化的，而且永远不可能在有限的时间中得出最优的路径。因此换句话说，要想得出相对满意的优化路径，是需要一定的运算时间的。所以RRT*算法的收敛时间是一个比较突出的研究问题。但不可否认的是，RRT*算法计算出的路径的代价相比RRT来说减小了不少。RRT*算法与RRT算法的区别主要在于两个针对新节点的重计算过程，分别为：

• 重新为选择父节点的过程， 比起RRT多了一个rewire的过程。
• 重布线随机树的过程

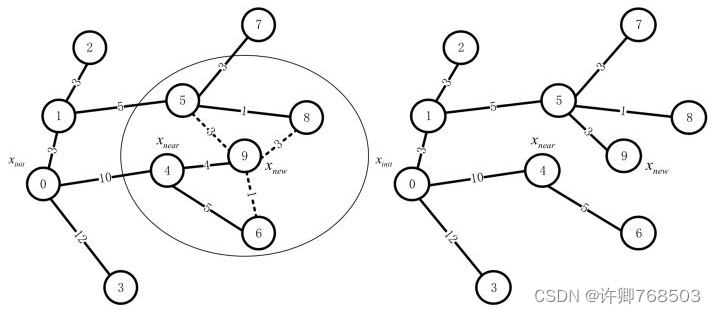
RRT*算法的基本步骤：

    <1>. 初始化：将起点添加到搜索树中。

    <2>. 循环：在搜索树中不断添加新节点，直到满足停止条件（例如找到目标点）为止。

               随机采样：从状态空间中随机采样一个点。

               最近邻节点：找到搜索树中距离采样点最近的节点。

               扩展：从最近邻节点沿着一定步长向采样点方向扩展，并检查路径是否与障碍物相交。

               连接：如果扩展后的路径不与障碍物相交，则将该节点添加到搜索树中，并更新与其相邻的节点。

     <3>. 优化路径：在建树完成后，对搜索树进行优化，尝试通过缩短路径长度或减少路径代价来改进路径质量。

              反向链接：从目标点开始，反向遍历搜索树，寻找到起点的最优路径。

             节点重新连接：在最优路径上尝试重新连接节点，使路径更直接或者更低代价。

      <4>. 返回结果：返回找到的最优路径。

           RRT*算法的优点是能够在保证快速搜索的同时，找到接近最优解的路径。然而，它的缺点是可能会受到采样点分布和步长选择的影响，导致搜索性能不稳定。

4、禁忌搜索算法

• 禁忌搜索算法是在贪婪思想的基础上发展的。贪婪算法最大的问题在于容易陷入局部最优，为了解决这个问题，研究人员引入了禁忌表，使其具有较强的全局搜索能力，禁忌表主要用于记录已经经过的点，其中内容是动态更新的，在这里的点在以后的搜索中将会直接跳过。
• 禁忌搜索算法要优于爬山启发式算法，爬山式启发算法局部搜索能力较强，收敛速度快但是容易陷入局部最优解，禁忌搜索算法在此基础上引入禁忌表后便可跳出局部最优解，转向寻找其他局部最优解，因此具备全局搜索能力。

5、动态规划（DP）算法

参考：https://blog.csdn.net/uytguytgf/article/details/119854809

 

 

 

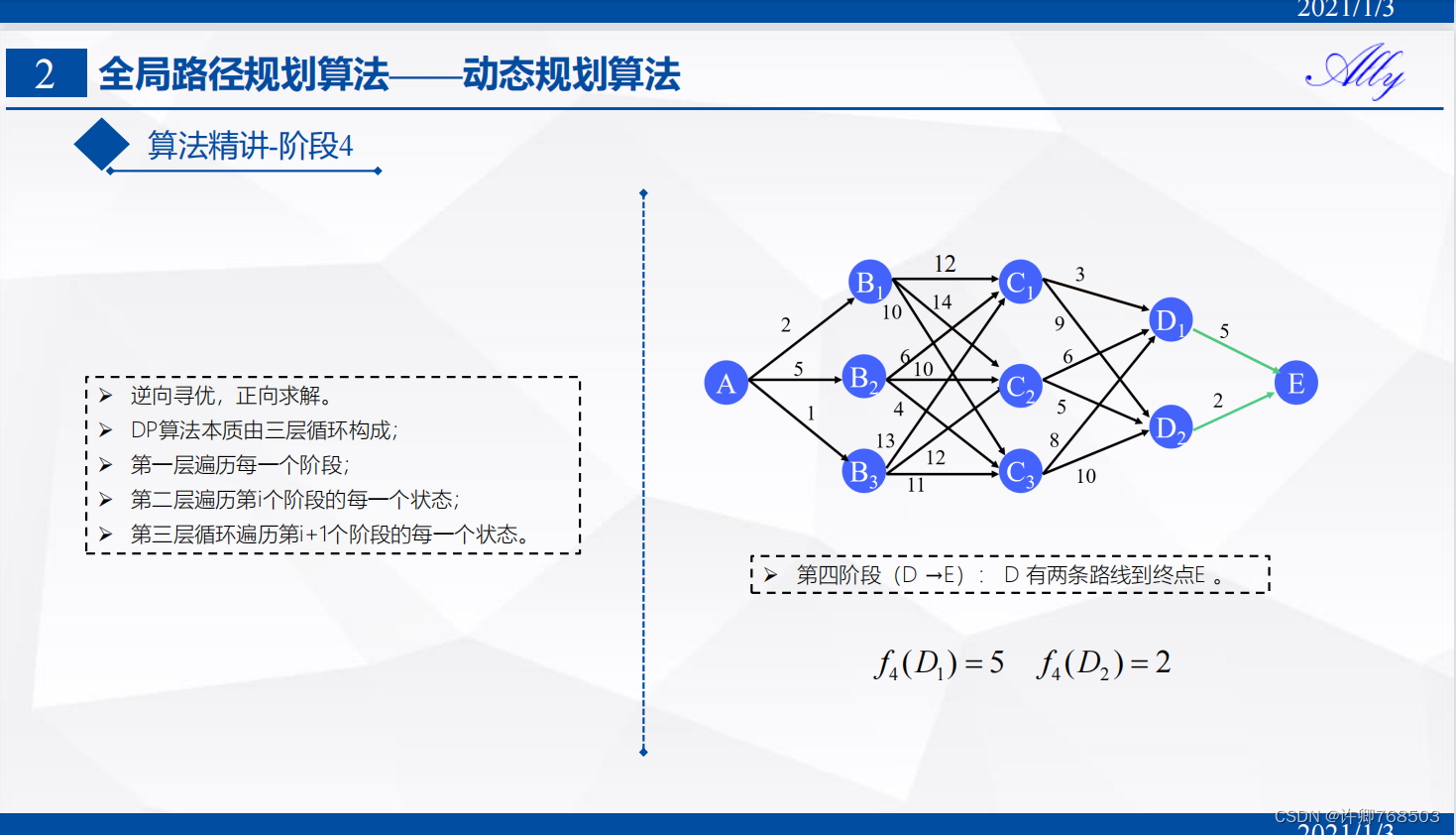
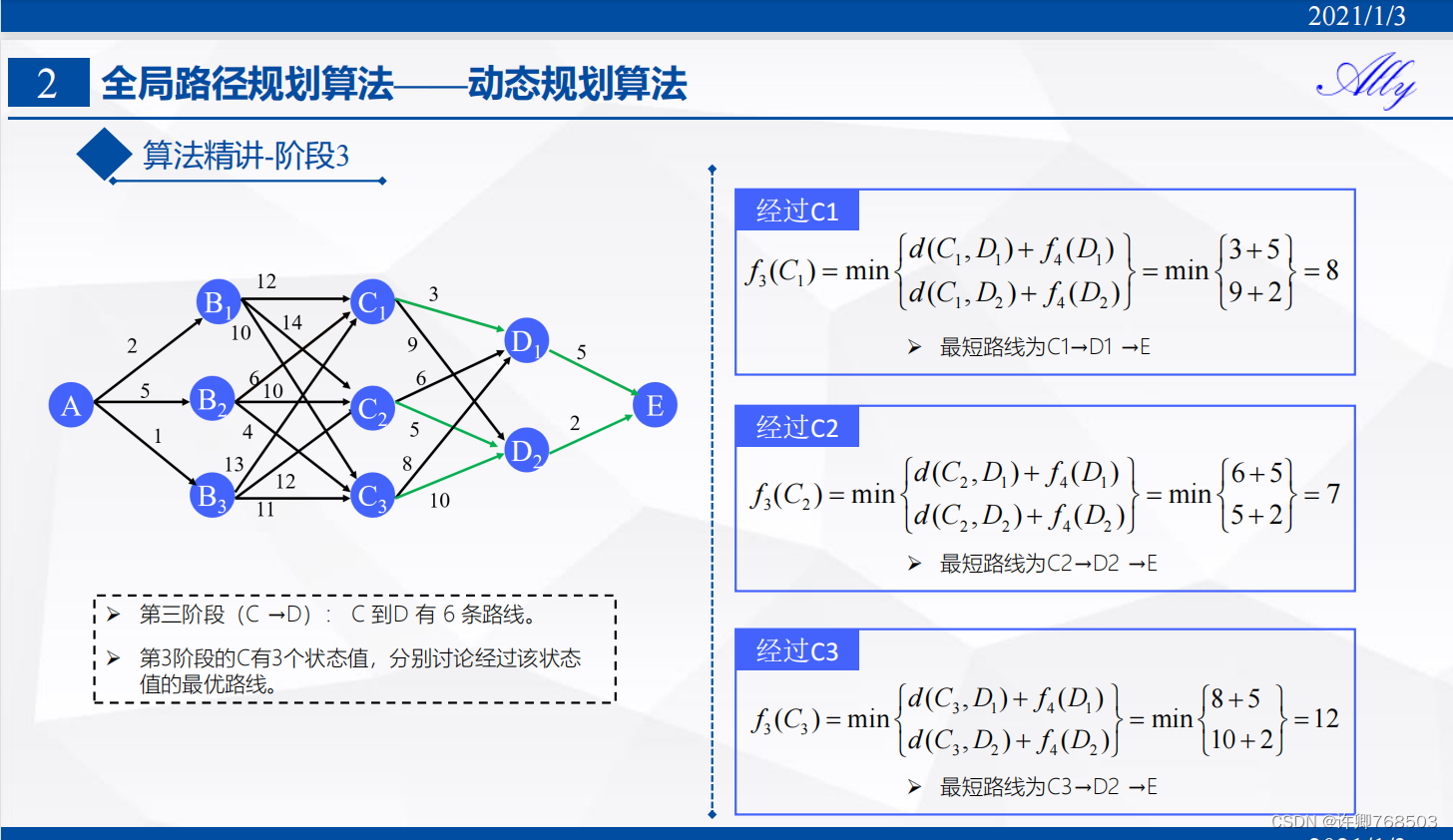
二、局部路径规划算法分类——传统算法

1、人工势场法——适用于静态环境下的路径规划

• 人工势场法是一种常用于局部路径规划的算法，通过将机器人视为带电荷的粒子，利用电荷之间的斥力和机器人与目标之间的引力来生成一种“势场”。

• 在人工势场中，障碍物被视为带有相同电荷的粒子，它们之间相互排斥。同时，目标点被视为带有相反电荷的粒子，吸引机器人朝着目标点移动。

• 机器人沿着势场梯度方向移动，直到达到目标点或者受到障碍物的斥力影响而停止。

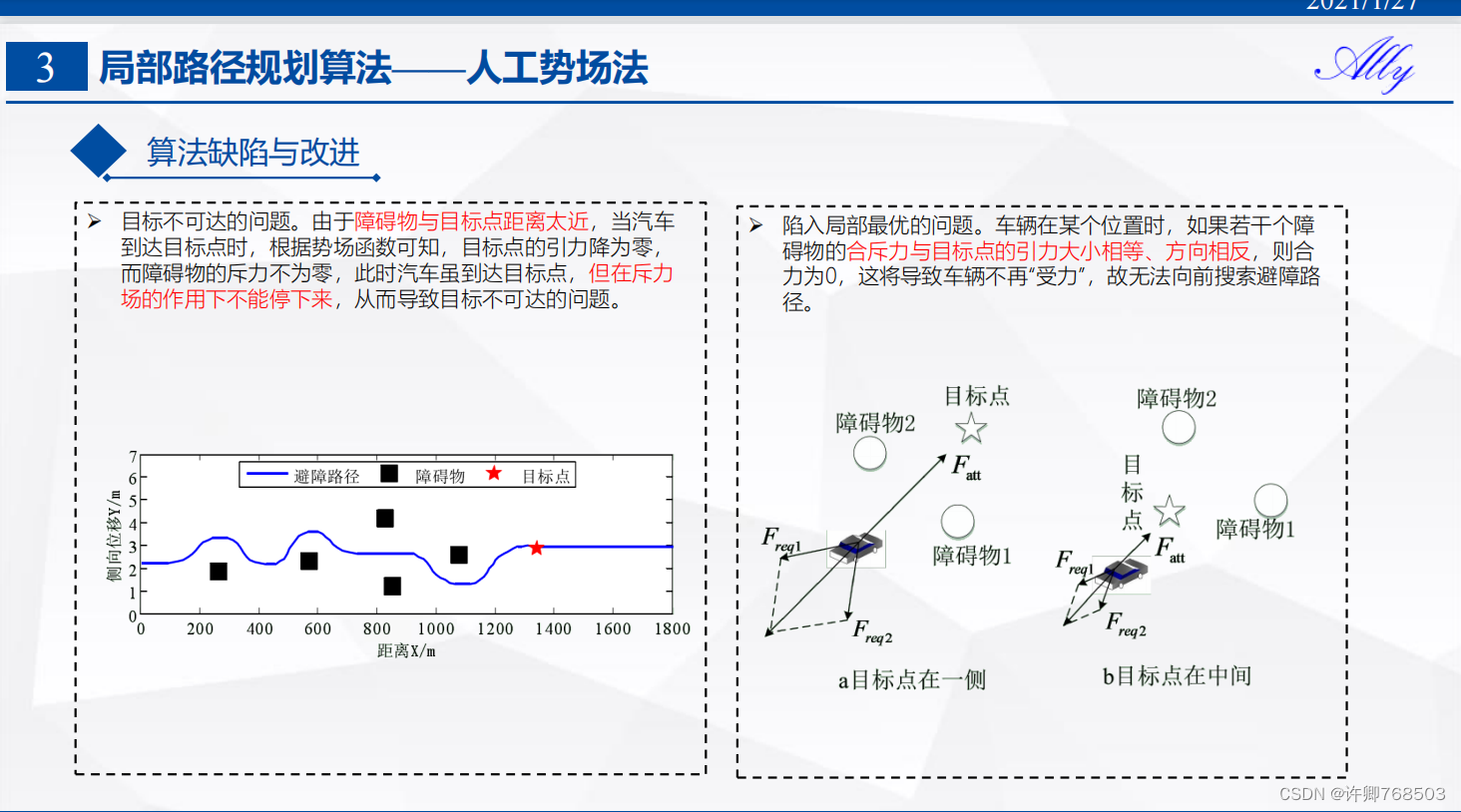
• 优点是简单易懂且易于实现，但存在局部最优解和对静态环境的依赖性的缺点。

• 由于障碍物与目标点距离太近，当汽车到达目标点时，根据势场函数可知，目标点的引力降为零，而障碍物的斥力不为零，此时汽车虽到达目标点， 但在斥力场的作用下不能停下来，从而导致目标不可达的问题。

 参考：https://blog.csdn.net/uytguytgf/article/details/119857711

 

2、 D*算法——适用于动态环境下的实时路径规划

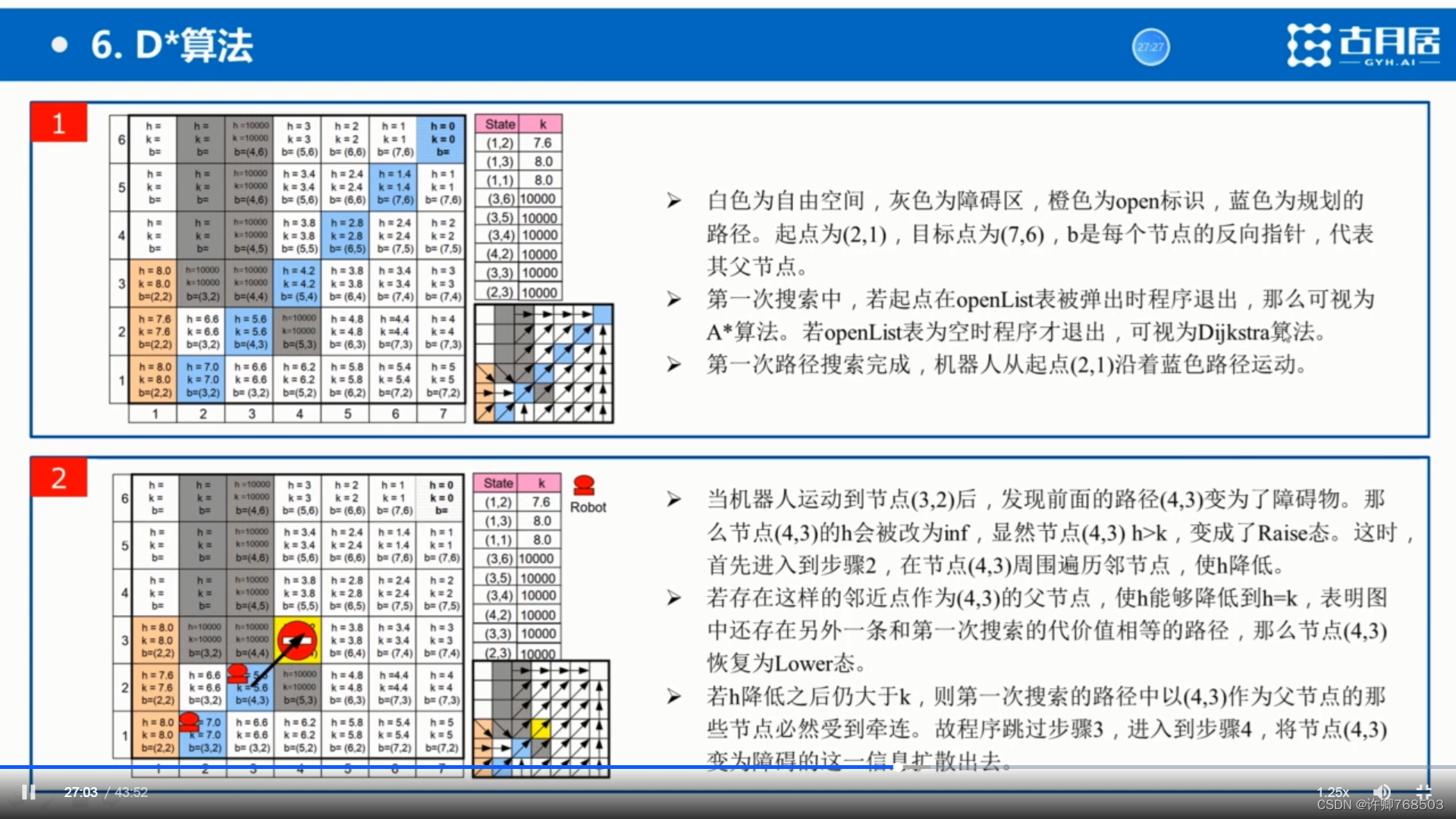
• D*算法是一种增量式局部路径规划算法，主要用于在动态环境中重新规划路径。
• 与传统的A算法不同，D算法在每次环境状态发生变化时，可以快速地更新路径规划而不需要重新从头开始搜索。
• D*算法基于状态空间图，使用反向搜索从目标点开始，通过局部代价更新来找到起点的最短路径。
• 当环境状态发生变化时，D*算法只需要根据变化的信息对受影响的路径进行局部更新，而不必重新计算整个路径。
• 优点是可以处理局部动态障碍，运算速度很快，适用于动态环境和实时路径规划，但需要对环境进行连续的状态更新和路径调整。
• 特点：反向增量式搜索算法

1. 1.反向：即算法从目标点开始向起点逐步搜索；
2. 2.增量式搜索：即算法在搜索过程中会计算每一个节点的距离度量信息H(x)，在动态环境中若出现障碍物无法继续沿预先路径搜索，算法会根据原先已经得到的每个点的距离度量信息在当前状态点进行路径再规划，无需从目标点进行重新规划。

• 利用了前一次的路径搜索信息，无需重复规划，提高了搜素效率
• 动态规划
• 栅格地图

 参考：https://blog.csdn.net/uytguytgf/article/details/128015530

3、 基于曲线拟合算法

• 圆弧与直线
• 多项式曲线
• 样条曲线
• 贝塞尔曲线
• 微分平坦

4、基于数值优化的算法

• 利用目标函数和约束对规划问题进行描述和求解。

5、LPA*算法

• 特点：正向增量式启发式
• Life Planning A*算法是一种基于A *算法的增量启发式搜索算法
• 搜索起始点为所设起点（正向搜索），按照Key值的大小作为搜索前进的原则，迭代到目标点为下一搜索点时完成规划；Key值中包含启发式函数h项作为启发原则来影响搜索方向；处于动态环境时，LPA*可以适应环境中障碍物的变化而无需重新计算整个环境，方法是在当前搜索期间二次利用先前搜索得到的g值，以便重新规划路径。
• 动态规划

6、D* lite算法

• 特点：反向增量式启发式
• 基于LPA_star 算法，D* lite与LPA*的主要区别在于搜索方向的不同，这就将Key[]定义中涉及到的目标点goal替换为起始点start的相应信息。
• D*_lite算法是先在给定的地图集中逆向搜索并找到一条最优路径。在其接近目标点的过程中，通过在局部范围的搜索去应对动态障碍点的出现。增量式算法的优势在于，各个点的路径搜索已经完成，在遇到障碍点无法继续按照原路径进行逼近时，通过增量搜索的数据再利用直接在受阻碍的当前位置重新规划出一条最优路径，然后继续前进。
• 动态规划

7、 DWA算法

• 动态窗口法是在速度（v,w）空间中采样多组速度，并模拟机器人在这些速度下一定时间（sim_period）内的轨迹，在得到多组轨迹以后，对这些轨迹进行评价，选取最优轨迹所对应的速度来驱动机器人运行。在评价过程中，会考虑到轨迹离障碍物的距离等。因此具备动态避障能力。
• 动作采样算法
• 运动学限制：1.小车速度的最大最小值 2.电机性能影响加速度3.预留刹车距离
• 全局路径规划出一条大致的路径，然后局部路径规划会把全局路径分割成很多段，大目标分成很多小目标，然后用DWA算法依次导航到每个小目标。

三、路径规划算法分类——智能算法

1、遗传算法——全局

• 遗传算法是一种搜索最优解的优化算法，通过模拟基因的选择、交叉、变异来进行仿真，在搜索过程中具备自我学习能力，能够自适应控制搜索过程来获取最优解。
• 选择是将父代个体的信息不做改变地复制传递给子代。每个个体对当前环境的适应度存在差异，在复制过程中，适应度高的个体被选中复制的概率大，经过不断迭代，群体中优秀个体比重越来越多，相应的路径也被不断优化。
• 交叉是将同一代不同个体间部分基因进行交换，产生新个体，产生的新个体将有可能生成更加优良的个体，相应的也会产生新的路径，从而提供更多选择。
• 变异是使个体基因发生突变，提供更多的基因组合，在小范围内寻找最优解，变异增加了基因种类，使得组合的时候有更多可能，算法寻优范围进一步扩大，变异操作对应于路径上可能是增删某个路径点或者移动路径点，这种操作具有不确定性，路径的适应值有提高或者降低的可能。
• 遗传算法具备较好地收敛性和全局搜索能力，但是局部搜索能力较差，并且容易陷入局部最优。

2、粒子群算法

• 粒子群算法是一种集群优化算法，其算法通过模拟群觅食行为相互合作机制寻求最优解。算法首先在空间中初始化粒子，然后粒子经过迭代寻找全局最优解。
• 粒子群算法结构简单、容易实现，但是算法比较容易陷入局部最优解，算法的收敛速度随着迭代次数和搜索范围增加不断变慢，甚至最终停滞，算法开始时参数设定比较依赖经验。

3、蚁群算法

• 蚁群算法是一种模拟蚂蚁觅食行为数学模型的一种正反馈算法，具有启发式思想，算法主要利用蚂蚁在觅食过程中释放信息素的原理，信息素浓度高的地方对蚂蚁有较大吸引力，最短路径上的蚂蚁信息素浓度最高，据此可以找到最优路径。
• 面对较为复杂的状态空间时，蚁群算法容易陷入局部最优，并且实时性难以保证，因此后来出现了很多蚁群算法与其他算法相结合的算法。