N皇后问题详解：回溯算法的应用与实践（dfs）_n皇后问题dfs

一.问题描述

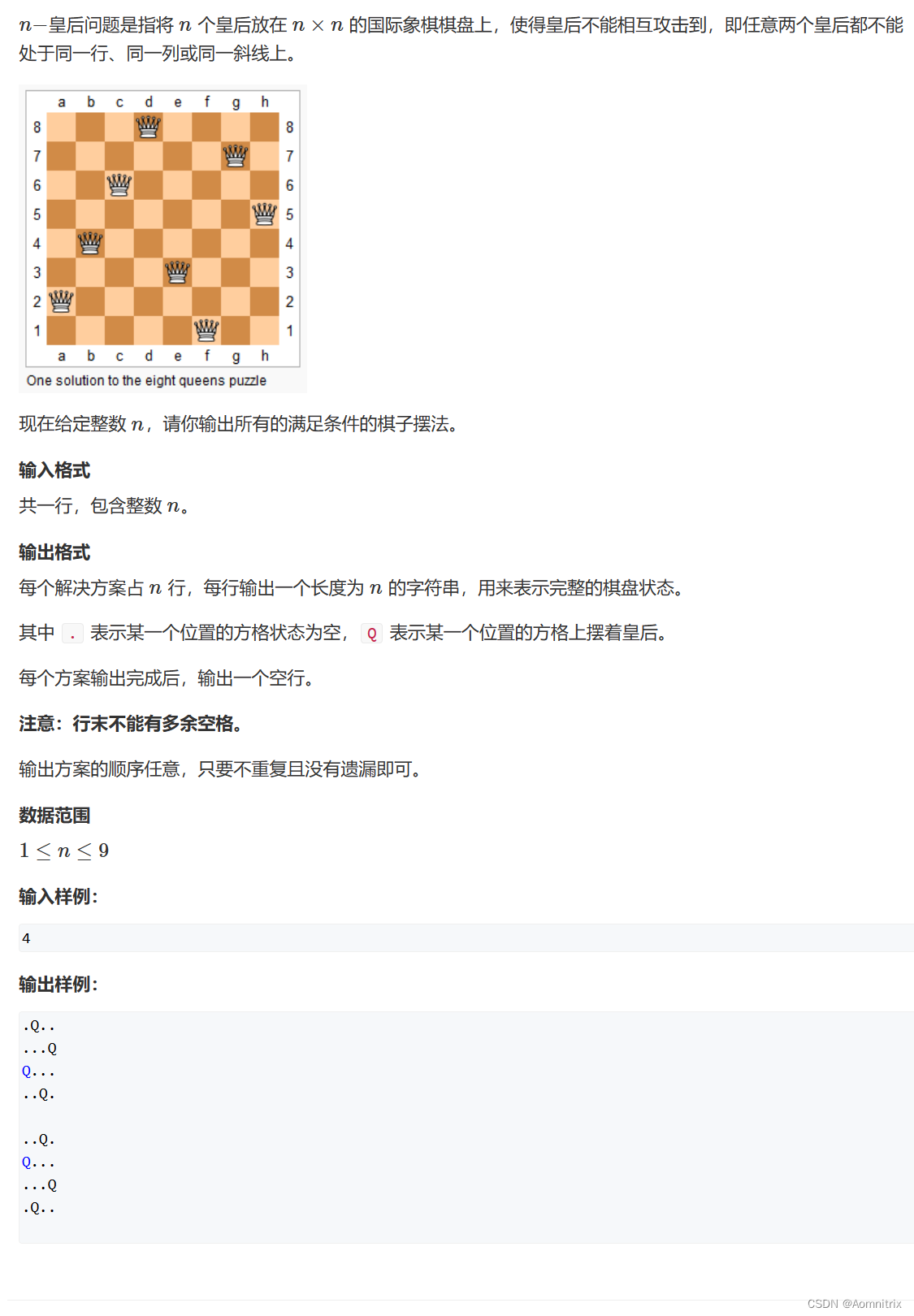
题目如上图所示，在一个n*n的国际象棋棋盘上怎么摆放能使得皇后互相攻击不到（也就是在任意一列、一行、一条对角线上都不存在两个皇后）

二.思路分析

1.DFS

想要解决这个问题，我们可以使用dfs也就是深度优先遍历，深度优先搜索的步骤为先递归到底再回溯上来，顾名思义，dfs是以深度为目标，一条路走到底，直到达到无路可走时，退回到上一步的状态，走其他路回溯上来。
这题我们就可以定义数组当做棋盘，遍历所有位置判断是否可以放置皇后（需要满足任意一列、一行、一条对角线上都不存在两个皇后），在遍历的过程中需要考虑剪枝的情况，减少解题时间复杂度。

三.代码实现与解析

1.分析

首先我们创建完数组模拟棋盘后，先要依据题意，将数组初始化为.

#include <iostream>
const int N = 20;
using namespace std;
char ret[N][N];

bool col[N], dg[N], udg[N];//标记列、对角线上是否已经有皇后

int n = 0;

void dfs(int u);

int main()
{
	cin >> n;
	for (int i = 0; i < n; i++)
		for (int m = 0; m < n; m++)
			ret[i][m] = '.';

	dfs(0);//dfs算法函数
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

紧接着就是dfs函数代码的实现逻辑：

void dfs(int u)
{
	if (u == n)
	{
		for (int i = 0; i < n; i++)
		{
			cout << ret[i] << endl;;
		}
		cout<< endl;
		return;
	}

	for (int i = 0; i < n; i++)
	{
		if (!col[i] && !dg[u + i] && !udg[n + i - u])
		{
			ret[u][i] = 'Q';
			col[i] = dg[u + i] = udg[n + i - u] = true;
			dfs(u + 1);
			ret[u][i] = '.';
			col[i] = dg[u + i] = udg[n + i - u] = false;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

需要重点理解的在for循环中i代表的是列数（遍历的是列），u代表的是层数，if判断当行、对角线均暂无皇后时，则可以在此放置皇后，并标识为已经放置，此时这一层的放置就结束了，所以接着就要递归下一层，之后就会分为两种情况：
1.递归到最后一层成功打印了这次的方案。接着就会向上回溯

ret[u][i] = '.';
col[i] = dg[u + i] = udg[n + i - u] = false;
1
2

执行恢复逻辑。
2.在后续层数遍历放置时，出现了不合法的情况（列数到达阈值依旧没有放置），此时就会剪枝，也是会回溯到上图代码进行恢复。

2.完整代码

#include <iostream>
const int N = 20;
using namespace std;
char ret[N][N];

bool col[N], dg[N], udg[N];

int n = 0;

void dfs(int u);

int main()
{
	cin >> n;
	for (int i = 0; i < n; i++)
		for (int m = 0; m < n; m++)
			ret[i][m] = '.';

	dfs(0);
	return 0;
}
void dfs(int u)
{
	if (u == n)
	{
		for (int i = 0; i < n; i++)
		{
			cout << ret[i] << endl;;
		}
		cout<< endl;
		return;
	}

	for (int i = 0; i < n; i++)
	{
		if (!col[i] && !dg[u + i] && !udg[n + i - u])
		{
			ret[u][i] = 'Q';
			col[i] = dg[u + i] = udg[n + i - u] = true;
			dfs(u + 1);
			ret[u][i] = '.';
			col[i] = dg[u + i] = udg[n + i - u] = false;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45