- 1软件测试,,30岁了,做了5年软件测试,只会功能测试怎么办?
- 2鸿蒙语言基础类库:【@ohos.convertxml (xml转换JavaScript)】
- 3计算机网络参考模型与5G协议
- 4营销广告电商行业如何实现降本提效?看这篇就够了!_降低电商营销成本
- 5如何参与github开源项目,成为contributor_github contributor
- 6命令行的艺术,命令行技巧总结_uconv命令
- 7Mac本地部署大模型-单机运行_mac 大模型 需要什么配置
- 82024年【非高危行业生产经营单位主要负责人及安全管理人员安全生产知识和管理能力】考试及非高危行业生产经营单位主要负责人及安全管理人员安全生产知识和管理能力考试题
- 9Vue与UnityWebGl交互通信(vue-unity-webgl的使用)
- 10在国产芯片上实现YOLOv5/v8图像AI识别-【1.4】YOLOv8的介绍及使用(训练、导出)更多内容见视频
(涛菜菜)c++及数据结构及算法经典题目总结_c++ 算法 数据结构题目
赞
踩
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
目录
一、链表相加(二)
假设链表中每一个节点的值都在 0 - 9 之间,那么链表整体就可以代表一个整数。
给定两个这种链表,请生成代表两个整数相加值的结果链表。
数据范围:0≤n,m≤10000000,链表任意值 0≤val≤9
要求:空间复杂度 O(n),时间复杂度 O(n)
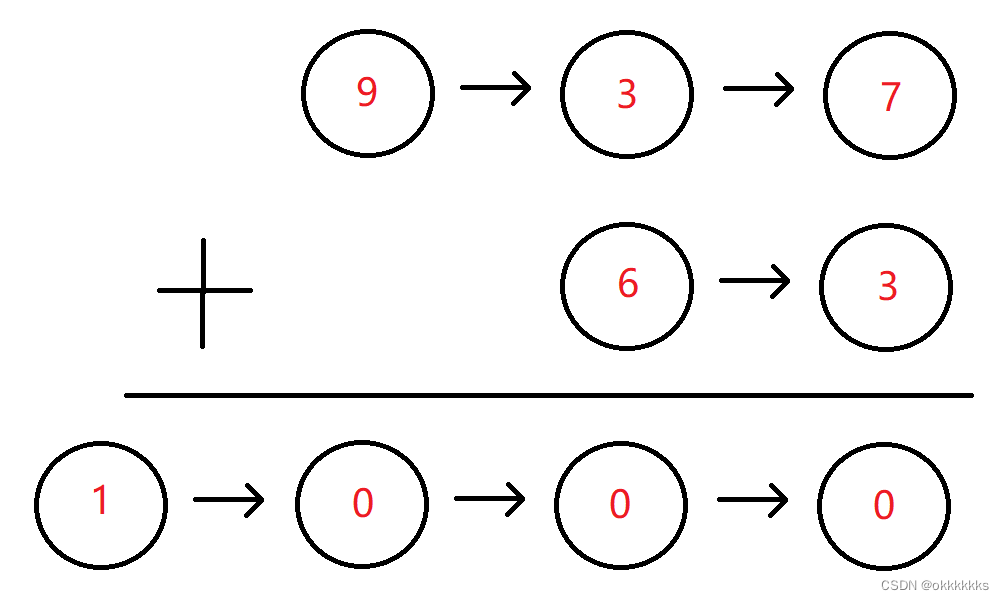
具体做法:
- step 1:任意一个链表为空,返回另一个链表就行了,因为链表为空相当于0,0加任何数为0,包括另一个加数为0的情况。
- step 2:相继反转两个待相加的链表,反转过程可以参考反转链表。
- step 3:设置返回链表的链表头,设置进位carry=0.
- step 4:从头开始遍历两个链表,直到两个链表节点都为空且carry也不为1. 每次取出不为空的链表节点值,为空就设置为0,将两个数字与carry相加,然后查看是否进位,将进位后的结果(对10取模)加入新的链表节点,连接在返回链表后面,并继续往后遍历。
- step 5:返回前将结果链表再反转回来
- class Solution {
- public:
- //反转链表
- ListNode* ReverseList(ListNode* pHead) {
- if(pHead == NULL)
- return NULL;
- ListNode* cur = pHead;
- ListNode* pre = NULL;
- while(cur != NULL){
- //断开链表,要记录后续一个
- ListNode* temp = cur->next;
- //当前的next指向前一个
- cur->next = pre;
- //前一个更新为当前
- pre = cur;
- //当前更新为刚刚记录的后一个
- cur = temp;
- }
- return pre;
- }
-
- ListNode* addInList(ListNode* head1, ListNode* head2) {
- //任意一个链表为空,返回另一个
- if(head1 == NULL)
- return head2;
- if(head2 == NULL)
- return head1;
- //反转两个链表
- head1 = ReverseList(head1);
- head2 = ReverseList(head2);
- //添加表头
- ListNode* res = new ListNode(-1);
- ListNode* head = res;
- //进位符号
- int carry = 0;
- //只要某个链表还有或者进位还有
- while(head1 != NULL || head2 != NULL || carry != 0){
- //链表不为空则取其值
- int val1 = head1 == NULL ? 0 : head1->val;
- int val2 = head2 == NULL ? 0 : head2->val;
- //相加
- int temp = val1 + val2 + carry;
- //获取进位
- carry = temp / 10;
- temp %= 10;
- //添加元素
- head->next = new ListNode(temp);
- head = head->next;
- //移动下一个
- if(head1 != NULL)
- head1 = head1->next;
- if(head2 != NULL)
- head2 = head2->next;
- }
- //结果反转回来
- return ReverseList(res->next);
- }
- };

二、反转链表
给定一个单链表的头结点pHead(该头节点是有值的,比如在下图,它的val是1),长度为n,反转该链表后,返回新链表的表头。
数据范围: 0≤n≤1000
要求:空间复杂度 O(1) ,时间复杂度 O(n) 。
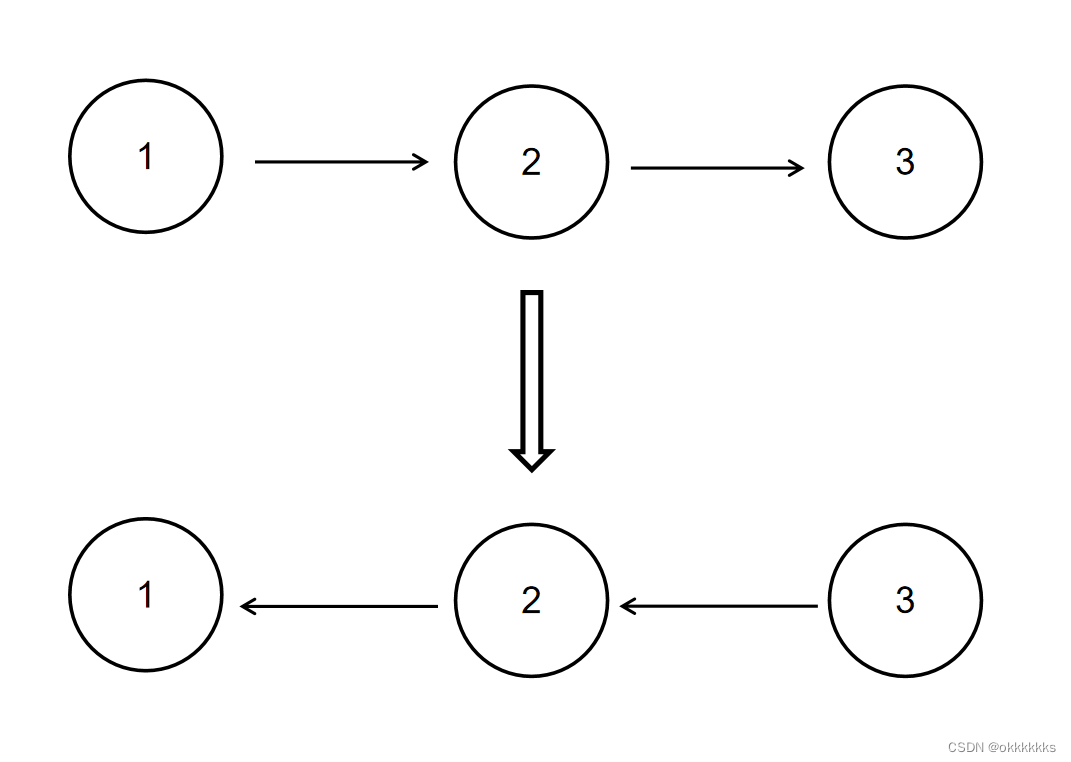
方法一: vector向量构造链表
可以先用一个vector将单链表的指针都存起来,然后再构造链表。
- class Solution {
- public:
- //1.使用栈解决
- //把节点链表一个一个入栈,全部入栈后再一个一个输出
- //2.构造链表
- //可以先用一个vector将单链表的指针都存起来,然后再构造链表。
- ListNode* ReverseList(ListNode* pHead) {
- if(!pHead)
- return nullptr;
- vector<ListNode*>v;
- while(pHead)
- {
- v.push_back(pHead);
- pHead=pHead->next;
- }
- reverse(v.begin(),v.end());//反转vector,也可以逆向遍历
- ListNode *head=v[0];
- ListNode *cur=head;
- for(int i=1;i<v.size();i++)//构造链表
- {
- cur->next=v[i];//当前节点的下一个指针指向下一个节点
- cur=cur->next;//当前节点后裔
- }
- cur->next=nullptr;//切记最后一个节点的下一个指针指向nullptr
- return head;
- }
- };

方法二:正规双向链表
- class Solution {
- public:
- //反转链表
- ListNode* ReverseList(ListNode* pHead) {
- if(pHead == NULL)
- return NULL;
- ListNode* cur = pHead;
- ListNode* pre = NULL;
- while(cur != NULL){
- //断开链表,要记录后续一个
- ListNode* temp = cur->next;
- //当前的next指向前一个
- cur->next = pre;
- //前一个更新为当前
- pre = cur;
- //当前更新为刚刚记录的后一个
- cur = temp;
- }
- return pre;
- }
- };

三,链表内指定区间反转
将一个节点数为 size 链表 m 位置到 n 位置之间的区间反转,要求时间复杂度 O(n),空间复杂度 O(1)。
数据范围: 链表长度 0<size≤1000,0<m≤n≤size,链表中每个节点的值满足∣val∣≤10000
给出的链表为 1→2→3→4→5→NULL, m=2,n=4,
返回 1→4→3→2→5→NULL.
方法一:栈
解题思路:
- 判断参数head是否为空,若空则直接返回;判断m是否等于n,相等则无需进行操作,直接返回;
- 由于题目给出的链表是不带头结点的,所以令i=1,work=head,首先用work指针,从链表头部开始进行遍历,遍历前m-1元素,最后一次遍历时,work指向第m个元素,同时以start指针记录work的当前位置以便下一次遍历时能够直接从第m个元素开始;
- 顺序遍历第m到第n位置的元素,并用栈进行存储;
- 再次从start出开始进行顺序遍历直到栈空,每遍历一个新结点时将栈顶元素赋值给当前结点,实现反转链表。
- ListNode* reverseBetween(ListNode* head, int m, int n)
- {
- if(!head || m == n)
- return head;
- ListNode *work = head;
- stack<int> stk;
- int i = 1;
- while(i <= m-1) { // 找到第m个结点
- work = work->next;
- ++i;
- }
- ListNode *start = work; // 记录第m个结点的指针
- while(i <= n) { // 记录第m到第n个结点的值
- stk.push(work->val);
- work = work->next;
- ++i;
- }
- work = start; // 从第m个结点开始遍历
- while(!stk.empty()) { // 赋值实现反转
- work->val = stk.top();
- stk.pop();
- work = work->next;
- }
- return head;
- }

四,合并两个排序的链表
输入两个递增的链表,单个链表的长度为n,合并这两个链表并使新链表中的节点仍然是递增排序的。
要求:空间复杂度 O(1),时间复杂度 O(n)

思路:
这道题既然两个链表已经是排好序的,都是从小到大的顺序,那我们要将其组合,可以使用归并排序的思想:每次比较两个头部,从中取出最小的元素,然后依次往后。这样两个链表依次往后,我们肯定需要两个指针同方向访问才能实现。
具体过程:
- step 1:判断空链表的情况,只要有一个链表为空,那答案必定就是另一个链表了,就算另一个链表也为空。
- step 2:新建一个空的表头后面连接两个链表排序后的节点,两个指针分别指向两链表头。
- step 3:遍历两个链表都不为空的情况,取较小值添加在新的链表后面,每次只把被添加的链表的指针后移。
- step 4:遍历到最后肯定有一个链表还有剩余的节点,它们的值将大于前面所有的,直接连在新的链表后面即可。
- class Solution {
- public:
- ListNode* Merge(ListNode* pHead1, ListNode* pHead2) {
- //一个已经为空了,直接返回另一个
- if(pHead1 == NULL)
- return pHead2;
- if(pHead2 == NULL)
- return pHead1;
- //加一个表头
- ListNode* head = new ListNode(0);
- ListNode* cur = head;
- //两个链表都要不为空
- while(pHead1 && pHead2){
- //取较小值的节点
- if(pHead1->val <= pHead2->val){
- cur->next = pHead1;
- //只移动取值的指针
- pHead1 = pHead1->next;
- }else{
- cur->next = pHead2;
- //只移动取值的指针
- pHead2 = pHead2->next;
- }
- //指针后移
- cur = cur->next;
- }
- //哪个链表还有剩,直接连在后面
- if(pHead1)
- cur->next = pHead1;
- else
- cur->next = pHead2;
- //返回值去掉表头
- return head->next;
- }
- };

五,字符串变形
对于一个长度为 n 字符串,我们需要对它做一些变形。
首这个字符串中包含着一些空格,就像"Hello World"一样,然后我们要做的是把这个字符串中由空格隔开的单词反序,同时反转每个字符的大小写。
比如"Hello World"变形后就变成了"wORLD hELLO"。
思路:
将单词位置的反转,那肯定前后都是逆序,不如我们先将整个字符串反转,这样是不是单词的位置也就随之反转了。但是单词里面的成分也反转了啊,既然如此我们再将单词里面的部分反转过来就行。
具体做法:
- step 1:遍历字符串,遇到小写字母,转换成大写,遇到大写字母,转换成小写,遇到空格正常不变。
- step 2:第一次反转整个字符串,这样基本的单词逆序就有了,但是每个单词的字符也是逆的。
- step 3:再次遍历字符串,以每个空间为界,将每个单词反转回正常。
- class Solution {
- public:
- string trans(string s, int n) {
- if(n==0)
- return s;
- string res;
- for(int i = 0; i < n; i++){
- //大小写转换
- if (s[i] <= 'Z' && s[i] >= 'A')
- res += s[i] - 'A' + 'a';
- else if(s[i] >= 'a' && s[i] <= 'z')
- res += s[i] - 'a' + 'A';
- else
- //空格直接复制
- res+=s[i];
- }
- //翻转整个字符串
- reverse(res.begin(), res.end());
- for (int i = 0; i < n; i++){
- int j = i;
- //以空格为界,二次翻转
- while(j < n && res[j] != ' ')
- j++;
- reverse(res.begin() + i, res.begin() + j);
- i = j;
- }
- return res;
- }
- };

六,二叉树的前序遍历(根左右)
具体做法:
- step 1:准备数组用来记录遍历到的节点值,C++可以直接用vector。
- step 2:从根节点开始进入递归,遇到空节点就返回,否则将该节点值加入数组。
- step 3:依次进入左右子树进行递归。
- class Solution {
- public:
- void preorder(vector<int>&res,TreeNode* root){
- //遇到空节点则返回
- if(root==NULL)
- return;
- //先遍历根节点
- res.push_back(root->val);
- //再去左子树
- preorder(res,root->left);
- //最后再去右子树
- preorder(res,root->right);
- }
- vector<int>preorderTraversal(TreeNode *root)
- {
- vector<int>res;
- //递归前序遍历
- preorder(res,root);
- return res;
- }
- };

七,二叉树的中序遍历(左根右)
具体做法:
- step 1:准备数组用来记录遍历到的节点值,C++可以直接用vector。
- step 2:从根节点开始进入递归,遇到空节点就返回,否则优先进入左子树进行递归访问。
- step 3:左子树访问完毕再回到根节点访问。
- step 4:最后进入根节点的右子树进行递归。
- class Solution {
- public:
- void inorder(vector<int>&res,TreeNode* root){
- //遇到空节点则返回
- if(root==NULL)
- return;
- //先遍历左子树
- inorder(res,root->left);
- //再遍历根节点
- res.push_back(root->val);
- //最后遍历右子树
- inorder(res,root->right);
- }
-
-
- vector<int> inorderTraversal(TreeNode* root) {
- vector<int>res;
- //递归中序遍历
- inorder(res,root);
- return res;
- }
- };

八. 二叉树的后序遍历(左右根)
- class Solution {
- public:
- void postorder(vector<int>&res,TreeNode*root){
- //遇到空节点则返回
- if(root==NULL)
- return;
- //先遍历左子树
- postorder(res,root->left);
- //再遍历右子树
- postorder(res,root->right);
- //最后遍历根节点
- res.push_back(root->val);
- }
- vector<int> postorderTraversal(TreeNode* root) {
- vector<int>res;
- //递归后续遍历
- postorder(res,root);
- return res;
- }
- };

九,二叉树的最大深度
具体做法:
- step 1:对于每个节点,若是不为空才能累计一次深度,若是为空,返回深度为0.
- step 2:递归分别计算左子树与右子树的深度。
- step 3:当前深度为两个子树深度较大值再加1。
- class Solution {
- public:
- int maxDepth(TreeNode* root) {
- //空节点没有深度
- if(root==NULL)
- return 0;
- //返回子树深度加1
- return max(maxDepth(root->left),maxDepth(root->right))+1;
- }
- };
十,二分查找
- class Solution {
- public:
- int search(vector<int>& nums, int target) {
- int l=0;
- int r=nums.size()-1;
- //从数组首尾开始,直到二者相遇
- while(l<=r){
- //每次检查中点的值
- int m=(l+r)/2;
- if(nums[m]==target)
- return m;
- if(nums[m]>target)
- r=m-1;
- else
- l=m+1;
- }
- return -1;
- }
- };

十一,最长公共前缀
给你一个大小为 n 的字符串数组 strs ,其中包含n个字符串 , 编写一个函数来查找字符串数组中的最长公共前缀,返回这个公共前缀。
进阶:空间复杂度 O(1),时间复杂度 O(n∗len)
方法:子串纵向查找
纵向遍历非常的直观,如下图所示,将每个字符串分别依次遍历每一列的元素,比较相同列上字符是否相同,若相同则比较下一个子串,若不同则最长公共前缀为上个遍历过的公共前缀。
- class Solution {
- public:
- //题目给出长度为n的子串,找出子串中最长的公共前缀。
- string longestCommonPrefix(vector<string>& strs) {
- if(!strs.size())//特判若子串为空则返回空值
- return "";
- for(int i=0;i<strs[0].size();i++)//枚举第一个子串的每个字符
- {
- for(int j=1;j<strs.size();j++)//枚举后面所有子串
- {
- if(strs[0][i]!=strs[j][i]||i==strs[j].size())
- {
- return strs[0].substr(0,i);
- }
- }
- }
- return strs[0];
- }
- };

十二,大数加法
以字符串的形式读入两个数字,编写一个函数计算它们的和,以字符串形式返回。
数据范围s.length,t.length≤100000,字符串仅由'0'~‘9’构成
思路:
字符串中就是从两个字符串的末尾开始相加。
step 1:若是其中一个字符串为空,直接返回另一个,不用加了。
step 2:交换两个字符串的位置,我们是s为较长的字符串,t为较短的字符串,结果也记录在较长的字符串中。
step 3:从后往前遍历字符串s,每次取出字符转数字,加上进位制,将下标转换为字符串t中从后往前相应的下标,如果下标为非负数则还需要加上字符串t中相应字符转化的数字。
step 4:整型除法取进位,取模算法去掉十位,将计算后的结果放入较长数组对应位置。
step 5:如果遍历结束,进位值还有,则需要直接在字符串s前增加一个字符‘1’。
- class Solution {
- public:
- string solve(string s, string t) {
- if(s.empty())
- return t;
- if(t.empty())
- return s;
- //让s为较长的,t为较短的
- if(s.length()<t.length())
- swap(s,t);
- //进位标志
- int carry=0;
- //从后往前遍历较长的字符串
- for(int i=s.length()-1;i>=0;i--)
- {
- //转数字加上进位
- int temp=s[i]-'0'+carry;
- //转较短的字符串相应的从后往前的下标
- int j=i-s.length()+t.length();//此处大数相加需要记住
- if(j>=0)
- temp+=t[j]-'0';
- carry=temp/10;
- temp=temp%10;
- s[i]=temp+'0';
- }
- if(carry==1)
- s='1'+s;
- return s;
- }
- };

十三,判断一个链表是否为回文结构
给定一个链表,请判断该链表是否为回文结构。
回文是指该字符串正序逆序完全一致。
数据范围: 链表节点数 0≤n≤105,链表中每个节点的值满足 ∣val∣≤107
具体做法:
- step 1:遍历一次链表,将元素取出放入辅助数组中。
- step 2:准备另一个辅助数组,录入第一个数组的全部元素,再将其反转。
- step 3:依次遍历原数组与反转后的数组,若是元素都相等则是回文结构,只要遇到一个不同的就不是回文结构。
- class Solution {
- public:
- bool isPail(ListNode* head) {
- vector<int>nums;
- //将链表元素取出一次放入数组
- while(head!=NULL) //需要记
- {
- nums.push_back(head->val);
- head=head->next;
- }
- vector<int>temp=nums; //对于向量赋值不需要一个一个数,直接就可以啦
- //准备一个数组继承翻转之后的数组
- reverse(temp.begin(),temp.end());
- for(int i=0;i<nums.size();i++)
- {
- //正向遍历和反向遍历是否相同
- if(nums[i]!=temp[i])
- return false;
- }
- return true;
- }
- };

十四,兑换零钱
给定数组arr,arr中所有的值都为正整数且不重复。每个值代表一种面值的货币,每种面值的货币可以使用任意张,再给定一个aim,代表要找的钱数,求组成aim的最少货币数。
如果无解,请返回-1.
数据范围:数组大小满足 0≤n≤10000 , 数组中每个数字都满足 0<val≤10000,0≤aim≤5000
具体做法:
- step 1:可以用dp[i]表示要凑出i元钱需要最小的货币数。
- step 2:一开始都设置为最大值aim+1,因此货币最小1元,即货币数不会超过aim.
- step 3:初始化dp[0]=0。
- step 4:后续遍历1元到aim元,枚举每种面值的货币都可能组成的情况,取每次的最小值即可,转移方程为dp[i]=min(dp[i],dp[i−arr[j]]+1).
- step 5:最后比较[aim]的值是否超过aim,如果超过说明无解,否则返回即可。
- class Solution {
- public:
- int minMoney(vector<int>& arr, int aim) {
- //小于1的都返回0
- if(aim<1)
- return 0;
- //dp[i]表示凑齐i元最小的货币数
- vector<int>dp(aim+1,aim+1);
- dp[0]=0;
- //遍历1~aim元
- for(int i=1;i<=aim;i++)
- {
- //每种面值货币都要枚举
- for(int j=0;j<arr.size();j++)
- {
- //如果面值不超过要凑的钱才可以用
- if(arr[j]<=i)
- {
- //维护最小值
- dp[i]=min(dp[i],dp[i-arr[j]]+1);
- }
- }
- }
- //如果最终答案大于aim代表无解
- return dp[aim]>aim?-1:dp[aim];
- }
- };

总结
珍惜当下的经历,生活就是一段段经历、修心,感受不同的经历,不要等到某个时候再去做什么事,人生没有过渡,你不能等到生活不再艰难了,才决定开始快乐。


