基于FPGA的数字图像处理- 图像分割【4.8】_fpga 图片画面拆分

10.4 基于FPGA的局部自适应分割

在本节中，我们将针对FPGA设计高斯局部自适应分割算法，并对 算法进行仿真验证。

10.4.1 算法转换

在10.3节中我们介绍了自适应分割的原理，这里不妨再把公式列 出来如下：

由公式可以看出，窗口的分割值是对图像进行开窗，并计算窗口 内的像素均值和标准差，分割值为像素均值和标准差的加权和。 在软件中，不考虑计算效率的情况下，这个计算是轻而易举的事 情。但是，我们注意到，在计算分割值的过程中，首先要计算窗口内 像素的方差，然后才能对方差进行开方计算标准差。在FPGA里面计算 开方是一件费时费力的工作，我们将尝试对不等式进行一个等价转 换。 为了便于理解，不妨假定目前的输入像素值为din，经算法处理后 的输出数据为dout，按照式（10-28），输出dout的计算方法如下：

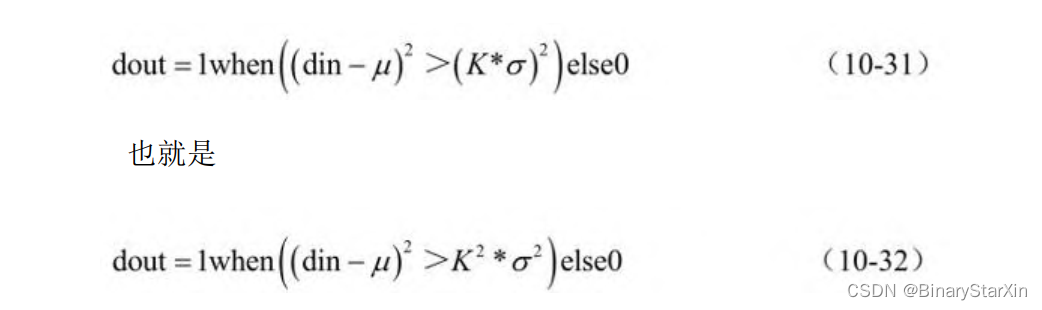
式（10-32）中，我们只需得到当前数据din，计算当前窗口内均 值和方差即可，这样就可避免了开方操作，简化了系统设计。 将式（10-27）代入式（10-32）中，则有

10.4.2 FPGA结构设计

同样，为充分利用FPGA的并行特性，我们采用流水线结构来实现 上述设计。由最终的算法等效表达式可知，FPGA需要完成以下计算工 作：

（1）计算当前窗口内的像素均值μ。 （2）计算当前窗口中心像素与均值之差的平方(din-μ)2 。 （3）将上式与225相乘，完成不等式左边的计算。 （4）计算当前窗口内225个所有像素值与均值之差的平方和，完 成不等式右边的计算。 （5）将第（3）步和第（4）步的结果进行比较，完成图像分割。 （6）完成行列对齐与边界处理。 根据以上设计步骤，我们给出FPGA的顶层设计框图如图10-13所 示。

        由图10-13可以看出，要完成图像的局部高斯分割工作，需要调用 一个均值计算模块mena_2d来计算当前窗口内的像素均值μ。 同时，为了在“同一时刻”计算出当前窗口内所有像素与窗口均 值的差平方，还必须要对以当前像素为中心的窗口的所有225个像素进 行缓存。对15×15个像素的缓存不是一件非常容易实现的事情，这里将指定尺寸的窗口缓存封装成一个模块，记为win_buf模块，把这个模 块的当前输出像素记为din_buf。 不等式左边的计算是非常简单的，窗口缓存的中间值即为当前像 素值，记为din_org，与均值做减法，求平方后再乘以225即可得到。 现在得到了窗口均值μ和当前窗口的像素队列225个din_buf，需 要做的是把窗口内225个din_buf分别与均值相减后计算平方。接下来 的工作就是把上面225个差平方的结果求和。同样，15×15个数的加法 运 算 也 是 非 常 麻 烦 的 ， 这 里 也 将 会 其 封 装 成 一 个 模 块 ， 记 为 add_tree。Add_tree的输出记为不等式右边结果。 将不等式进行比较，利用比较结果对原图像进行分割即可。

10.4.3 子模块设计

        在7.2节中，我们已经详细介绍了窗口均值的计算方法，在这里不 再详细介绍了。本节将详细介绍一个新的窗口缓存模块win_buf，以及 多数据累加模块add_tree。 1.窗口缓存模块win_buf 本模块不做任何算法上的处理，只是负责将当前输入像素的二维 窗口元素缓存并组成一个一维的向量输出。 模块的构建非常简单，对图像分别做行列方向的延迟即可。对于 行方向上的延迟，可以采用行缓冲来实现，对于列方向上的延迟，则 采用寄存器来实现。 设定需要缓存的窗口尺寸为KSZ，则需要KSZ-1个行缓存，以及 KSZ×KSZ个寄存器来实现。 我们将以7×7的窗口缓存模块为例来说明，其设计框图如图10-14 所示。

我们不难把这个电路扩展到尺寸为15×15的窗口中去，在图10-14 中也重点标注出了窗口中心像素点。这个中心像素点就代表当前处理 的像素中心，实际图中的7×7矩阵就是当前像素的开窗缓冲区。当然 也可以用此电路来实现图像的卷积运算，例如排序、Sobel算子、高斯 滤波，或者均值求取等。 2.数据累加模块add_tree 数据累加模块负责将窗口内所有元素与均值之差的平方相加，这 里还是采用之前的加法思路：每个加法器限制两个输入，这样，对于 225个数据，在第一个时钟，共有112对数据进行相加。同时把剩余的 一个数据进行缓存，第二个时钟有56对数据进行相加，同时将之前的 数据缓存，依此类推，如图10-15所示。

问题的关键在于如何描述这一个电路。当然可以采用最笨的方 法：将上述电路中所有的寄存器及加法器和中间信号均描述出来。这 样带来的工作量是非常大的，带来的问题还容易出错，代码可维护性 和可读性极差。 如果再仔细分析上述框图，就很容易发现规律：除了最后一个时 钟直接完成两个数的相加，在其他的每个时钟内，加法运算电路都是 相似的，不同的只是待加的数目不同。 为了总结出这个规律，我们列出几个时钟如下： 第1个时钟：需完成225个数据相加，共需112个加法器，113个寄 存器。 第2个时钟：需完成113个数据相加，共需56个加法器，57个寄存 器。 第3个时钟：需完成57个数据相加，共需28个加法器，29个寄存 器。

对应的C语言算法如下所示。
/*num 为数组的长度，a 为待求和的数组*/
/*递归结束条件为最后只剩两个元素相加*/
int sum(int num,int *a)
{
int y[100]; //缓存if (num==2)
{
return (a[0]+a[1]); //直到最后剩下两个数据相加作为最
后的和返回
}
else
{
int temp=num;
num=num/2;
for (int i=0;i＜num;i++)
{
y[i]=a[2*i]+a[2*i+1];
}
if (temp%2==0) //如果个数能被 2 整除，则没有单独剩余的
数据
{
sum(num,y); //对此新向量进行递归计算
}
else //否则就会剩一个数据无法配对，
{
y[num]=a[temp‐1]; //对单独的数据进行缓存
sum(num+ num %2,y); //将此数据和前面形成的向量组成一个
新向量
}
} }

读者需注意，到目前为止，我们所有的讨论都是基于图10-15所描 述的电路图，只是用了另外一种电路描述方式而已，我们将在后面详 细介绍递归求和的代码设计。 图10-16是递归求和的框图，可见，我们只是把图10-15后面的部 分重新封装起来了而已。

3.顶层模块gauss_segment_2d 有了以上几个模块，顶层的设计就十分简单了。需实例化一个均 值求取模块mean_2d，求取当前窗口的均值，实时实例化一个窗口缓存 模块win_buf。需要注意的是，均值求取模块需要一定的latency，需 要将输入数据预期延迟对齐后再进行窗口缓存。Winbuf输出中心像素与均值进行差平方运算后，再进行乘255运算计算不等式左边结果；输 出其他像素分别与均值进行差平方运算，将计算结果送入例化的 add_tree模块计算和，作为不等式右边结果，最后根据比较结果完成 图像分割。计算框图如图10-17所示。

10.4.4 Verilog代码设计

1.窗口缓存模块win_buf
模块定义如下：

module win_buf(
rst_n,
clk,
din_valid, //输入有效
din, //输入数据流
dout, //输出向量
dout_org, //输出中心像素值
vsync, //输入场同步
vsync_out, //输出场同步is_boarder, //边界信息
dout_valid //输出有效
);
parameter DW = 14; //数据位宽
parameter KSZ = 15; //处理窗口
parameter IH = 512; //图像高度
parameter IW = 640; //图像宽度
input rst_n;
input clk;
input din_valid;
input [DW-1:0]din;
output [DW*KSZ*KSZ-1:0]dout; //输出为KSZ*KSZ向量
output [DW-1:0]dout_org; //输出中心像素
input vsync;
output vsync_out;
output is_boarder;
output dout_valid;
localparam num_all = KSZ * KSZ; //窗口数据总数
//窗口寄存器
reg [DW-1:0]p[0:num_all-1];
//例化KSZ-1个行缓存
generate
begin : line_buf
genvar i;
for (i = 0; i ＜= KSZ - 2; i = i + 1)
begin : buf_inst
line_buffer #(DW,IW)line_buf_inst(
.rst(rst_all),
.clk(clk),
.din(line_din[i][DW - 1:0]),
.dout(line_dout[i][DW - 1:0]),
.wr_en(line_wren[i]),
.rd_en(line_rden[i]),
.empty(line_empty[i]),
.full(line_full[i]),
.count(line_count[i])
);
end
end
endgenerate
//将输入接入延时电路
if (valid == 1'b1)
p[0]＜= #1 din;
//列延迟电路
for (k = 0; k ＜= KSZ - 1; k = k + 1)
for (j = 1; j ＜= KSZ - 1; j = j + 1)
if ((line_valid[k * KSZ + j - 1]) == 1'b1)
p[k * KSZ + j]＜= #1 p[k * KSZ + j - 1];
//行延迟电路
for (k = 1; k ＜= KSZ - 1; k = k + 1)
if ((line_rden[k - 1]) == 1'b1)
p[k * KSZ]＜= #1 line_dout[k - 1];
//输出窗口缓存generate
begin : xhdl2
genvar i;
for (i = 1; i ＜= num_all; i = i + 1)
begin : out_dat_gen
assign dout[i * DW - 1:(i - 1) * DW]= p[i - 1];
end
end
endgenerate

//输出中心像素 

assign dout_org = p[med_idx]; 2.累加和模块add_tree 模块完成指定宽度的数据向量的加法运算，模块定义如下：

module add_tree(
rst_n,
clk,
din_valid,
din, //输入数据向量
dout, //输出和
dout_valid
);
parameter DW = 14; //本次递归的数据位宽
parameter KSZ = 225; //本次递归的尺寸
localparam KSZ_new = (((KSZ) >> 1) + (KSZ%2));//下次递
归的尺寸
localparam HALF_EVEN = (KSZ >> 1); //本次需做加法的数目
localparam DW_new = (DW + 1); //下次递归的数据位宽input rst_n;
input clk;
input din_valid;
input [KSZ*DW-1:0]din; //输入数据为KSZ的数据向量
output [2*DW-1:0]dout; //输出位宽定为2*DW，需注意不要溢
出
output dout_valid;
reg [DW:0]dout_r;
reg dout_valid_r;
reg dout_valid_tmp;
reg [DW:0]din_reg;
reg [KSZ_new*(DW+1)-1:0]dout_tmp;
wire [2*DW_new-1:0]dout_tmp2;
wire dout_valid_tmp2;
assign dout = dout_tmp2[DW * 2 - 1:0];
assign dout_valid = dout_valid_tmp2;
generate //最后一次递归调用 只剩最后两个数据 直接相加即可
if (KSZ == 2)
begin : xhdl2
always @(posedge clk)
begin
dout_r ＜= #1 ({1'b0,din[DW - 1:0]} + din[2 * DW -
1:DW]);
dout_valid_r ＜= #1 din_valid;
end
assign dout_tmp2[DW:0]= dout_r;
assign dout_tmp2[DW * 2 - 1:DW + 1]= {DW-1{1'b0}};assign dout_valid_tmp2 = dout_valid_r;
end
endgenerate
//中间递归调用
generate
if ((～(KSZ == 2)))
begin : xhdl3
begin : xhdl0
genvar i;
for (i = HALF_EVEN; i >= 1; i = i - 1)//两个两个进
行加法运算
begin : gen_add_pipe
always @(posedge clk)
begin
if(din_valid==1'b1)
dout_tmp[(i) * (DW + 1) - 1:(i - 1) * (DW
+ 1)]＜=
#1(({1'b0,din[(i * 2) * DW - 1:(i * 2)
* DW - DW]}) +
din[(i * 2 - 1) * DW - 1:(i * 2 - 1) *
DW - DW]);
end
end
end
always @(posedge clk)
dout_valid_tmp ＜= #1 din_valid;//输入尺寸为奇数 必然剩一个无法配对 需将其缓存 同时与加
法结果组成新的向量进行下一次递归运算
if (KSZ % 2 == 1)
begin : xhdl4
always @(posedge clk)
din_reg[DW:0]＜=#1({1'b0,din[KSZ*DW-1:(KSZ-
1)*DW]});
always @(din_reg)
dout_tmp[KSZ_new * (DW + 1) - 1:(KSZ_new - 1) *
(DW + 1)]
＜= din_reg;
end
//进行下一次递归运算
add_tree #(DW_new,KSZ_new)
addtree_inst(
.rst_n(rst_n),
.clk(clk),
.din_valid(dout_valid_tmp),
.din(dout_tmp[KSZ_new * (DW + 1) - 1:0]),
.dout(dout_tmp2),
.dout_valid(dout_valid_tmp2)
);
end
endgenerate
endmodule

3.顶层模块gauss_segment_2d
//模块定义如下：
 

module gauss_segment_2d(
rst_n,
clk,
din_valid, //输入有效
din, //输入数据
dout, //输出数据
vsync, //输入场同步
vsync_out, //输出场同步
dout_valid //输出有效
);
//首先进行均值运算
Mean_2D #(DW,KSZ,IH,IW)
mean(
.rst_n(rst_n),
.clk(clk),
.din(din),
.din_valid(din_valid),
.din_valid_delay(din_valid_delay),
.din_delay(din_delay),
.dout_valid(mean_valid),
.vsync(vsync),
.vsync_out(mean_vsync),
.is_boarder(is_boarder_mean),
.dout(dout_mean) //均值结果
);
//输入延时 等待均值运算结束
always @(posedge clk)begin
if (rst_all == 1'b1)
begin
din_valid_delay_r ＜= {mean_latency{1'b0}};
din_delay_r ＜= {mean_latency*DW-1+1{1'b0}};
end
else
begin
din_valid_delay_r ＜= #1
({din_valid_delay_r[mean_latency -
2:0],din_valid});
din_delay_r ＜= #1
({din_delay_r[(mean_latency - 1) * DW -
1:0],din});
end
end
//缓存当前窗口
win_buf #(DW,KSZ,IH,IW)
orignal_buf(
.rst_n(rst_n),
.clk(clk),
.din_valid(din_valid_delay_r[mean_latency -
1]),
.din(din_delay_r[mean_latency*DW-1:
(mean_latency-1)*DW]),
.dout(din_new),
.dout_org(din_org),.vsync(vsync),
.is_boarder(new_boarder),
.dout_valid(din_new_valid)
);
//计算窗口内所有像素的差平方
generate
begin : xhdl0
genvar i;
for (i = 0; i ＜= KSZ * KSZ - 1; i = i + 1)
begin : cal_square//首先计算差值
always @(*) diff_tmp[i]＜= ((({din_new[(i +
1) * DW - 1:(i)
* DW],4'b0000}) > ({dout_mean[DW +
2:0],1'b0}))) ?
(({din_new[(i + 1) * DW - 1:(i) *
DW],4'b0000}) -
({dout_mean[DW + 2:0],1'b0})) :
(({dout_mean[DW + 2:0],1'b0}) -
({din_new[(i + 1) * DW-
1:(i) * DW],4'b0000}));
assign #1 square_temp[i]=(diff[i]*
diff[i]);//接着计算平方值
always @(posedge clk)
begin
if (din_new_valid == 1'b1 & mean_valid ==
1'b1 & ((～
(is_boarder_mean))) == 1'b1)diff[i]＜= #1 diff_tmp[i];
if (mul_valid == 1'b1)
//将结果组成一个新的向量方便加法运算
square[(i + 1) * DW_SQR - 1:(i) * DW_SQR]＜
= #1
({square_temp[i],4'b0000});
end
end
end
endgenerate
//将窗口内平方差相加
add_tree #(DW_SQR,KSZ_SQR)
square_total(
.rst_n(rst_n),
.clk(clk),
.din_valid(mul_valid_r),
.din(square_all_input),
.dout(add_all),
.dout_valid(square_all_valid)
);
//不等式左边乘以225 = 128 + 64 + 32 + 1
always @(posedge clk)
begin
if (mul_valid_r == 1'b1)
begin
square_org1 ＜=
({8'b00000000,square_org_tmp}) + ({1'b0,square_org_tmp,7'b0000000});
square_org2 ＜=
({2'b00,square_org_tmp,6'b000000}) +
({3'b000,square_org_tmp,5'b00000});
end
if (mul_valid_r2 == 1'b1)
square_org ＜= square_org1 + square_org2;
square_org_r ＜= ({square_org_r[(latency - 1) *
DW_SQR_TOTAL -
1:0],square_org});
end
assign square_all_input = square[KSZ * KSZ * DW_SQR -
1:0];
//利用两边不等式结果做阈值分割
assign square_all = add_all[DW_SQR_TOTAL - 1:0];
assign square_tmp1 = ({4'b0000,square_all});
assign square_tmp2 = {DW_SQR_TOTAL+4{1'b0}};
assign square_tmp3 = {DW_SQR_TOTAL+4{1'b0}};
always @(posedge clk)
begin
if (square_all_valid == 1'b1)
begin
sigma_square1 ＜= square_tmp1 + square_tmp3;
sigma_square2 ＜= square_tmp2;
end
if (square_all_valid_r == 1'b1)
sigma_square ＜= sigma_square1 + sigma_square2;end
assign square_org_last = ({4'b0000,
square_org_r[latency *
DW_SQR_TOTAL - 1:(latency - 1) * DW_SQR_TOTAL]});
assign din_final = din_org_r[(sigma_latency) * DW - 1:
(sigma_latency
- 1) * DW];
//分割结果
assign dout_cmp = ((square_org_last >
sigma_square)) ? {DW{1'b0}} :{DW{1'b1}};
//边界处理
assign dout_no_board = (((board_r[sigma_latency -
1] | ( ～ (valid_r[sigma_latency - 1]))) == 1'b1)) ?
{DW{1'b0}} : dout_cmp;
//输出数据
always @(posedge clk)
begin
if (rst_all == 1'b1)
dout ＜= {DW{1'b0}};
else
dout ＜= #1 dout_no_board;
end