龙格库塔（Runge-Kutta）法求四元数微分方程_四元数微分方程+龙格库塔法

一、背景知识

陀螺仪是一种测量角运动的装置，在导航、运动检测、姿态检测等方面有着非常广泛的应用。在惯性测量单元（IMU）中，陀螺仪起主要作用，加速度计往往用来辅助，通过滤波算法和融合算法可以由IMU输出的数据得到物体的姿态。事实上，如果陀螺仪的性能足够好，就可以只通过对陀螺仪得到准确的姿态了。这篇文章要解决的问题就是如何用陀螺仪的数据得到物体的姿态。

1. 坐标系

陀螺仪输出的是角速度，那么对角速度积分是不是就能得到物体在空间中的姿态呢？事实上并非如此，在这里需要理解三个坐标系：世界坐标系、载体坐标系和惯性坐标系。
世界坐标系又称作宇宙坐标系或者全局坐标系，是其他坐标系的参考系，我们可以在世界坐标系下去描述其他坐标系或者物体的位置和姿态。
载体坐标系，又称作机体坐标系、物体坐标系等，顾名思义，这个坐标系是物体上的坐标系，会跟随物体的运动而运动。以手机为例，一般会在手机上建立如下所示的右手坐标系，这个坐标系就是一个载体坐标系。陀螺仪安装在手机上，如果忽略芯片本身和安装带来的非正交误差的话，可以认为陀螺仪的坐标系和手机的坐标系是同一个坐标系。所以，陀螺仪输出的角速度实际上是手机载体坐标系的角速度，直接对陀螺仪角速度积分得到的不是我们从世界坐标系看到的手机的姿态角度。需要将陀螺仪角速度转换到惯性坐标系，然后再积分才能得到物体的姿态。

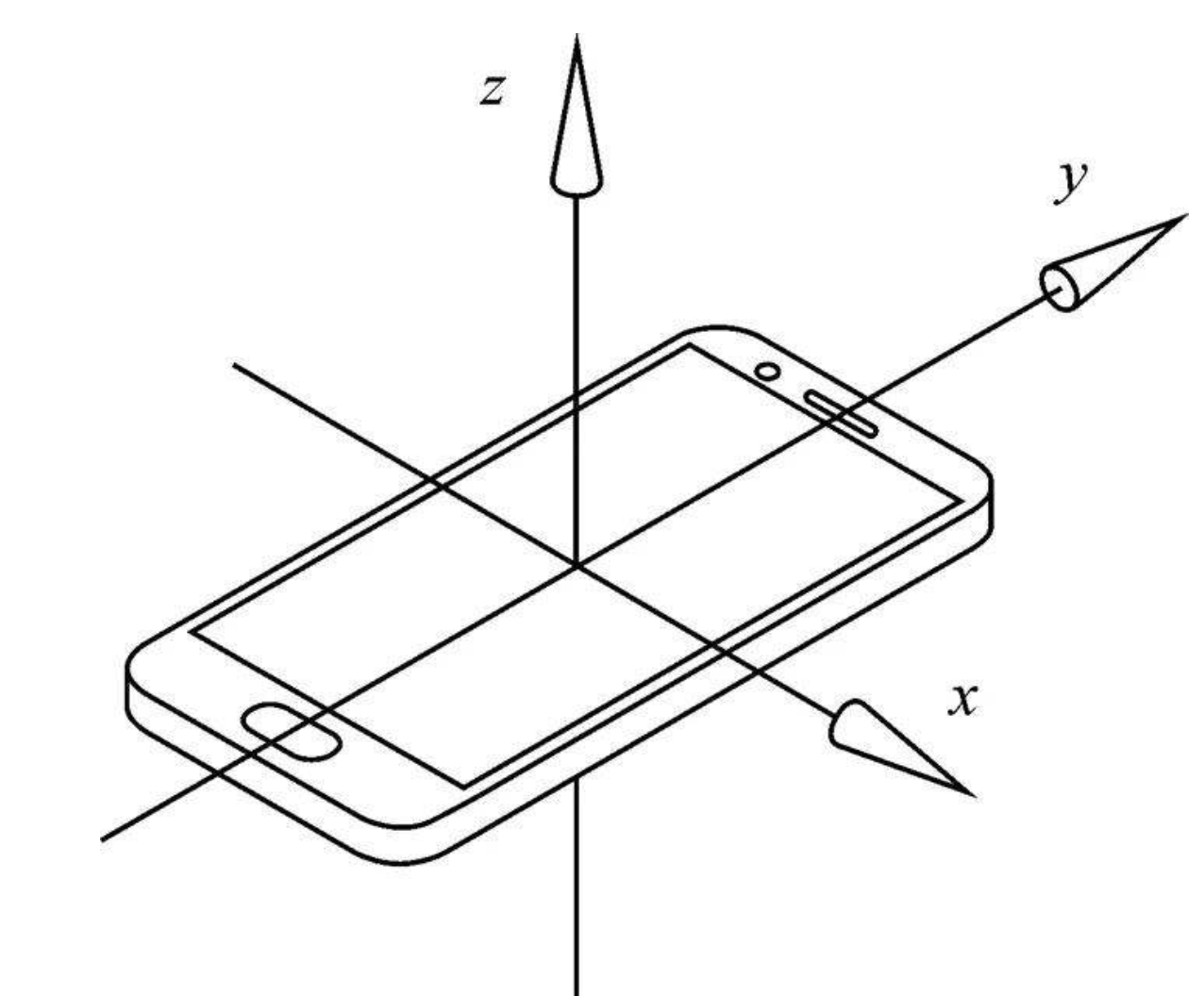
惯性坐标系是为了简化世界坐标系和载体坐标系的转化而产生的。两个直角坐标系的关系包括旋转和位移。惯性坐标系的原点和载体坐标系的原点是同一个，所以通过旋转关系，两个坐标系就能够重合。而惯性坐标系通过位移就能够和世界坐标系重合。

2. 四元数

表示一个物体的姿态有很多种方法，最主流的方法有欧拉角、旋转矩阵、轴角，以及四元数。这些表示方法各有优缺点，但综合来说，四元数是一种非常适合在工程上表示姿态的方法。四元数可以理解成复数的扩展，它有一个实部和三个虚部，表示成$q=w+x\ast i+y\ast j+z\ast k$，其中$i\ast i=-1,j\ast j=-1,k\ast k=-1,i\ast j\ast k=-1$。四元数有自己一套运算法则和性质，后面在其他文章具体阐述，这里介绍几个重要的点。

四元数的矩阵形式

类似复数，四元数也有模长或者称为2-范数，即 ∥ q ∥ = w 2 + x 2 + y 2 + z 2

$$\begin{Vmatrix}q\end{Vmatrix}$$ =\sqrt {w^2+x^2+y^2+z^2} ∥∥​q​∥∥​=w2+x2+y2+z2 ​，如果$\Vert \begin{array}{c}q\end{array}\Vert =1$，则称这个四元数位单位四元数，单位四元数有如下性质：$q^{-1}=q^{\ast }$。
假设两个四元数相乘$q_1{q}_2$，其中$q_1=a+b\ast i+c\ast j+d\ast k$，$q_2=e+f\ast i+g\ast j+h\ast k$，则
$$\begin{array}{rl}{q}_1\ast q_2=& ae+af\ast i+ag\ast j+ah\ast k+\\ & be\ast i-bf+bg\ast k-bh\ast j+\\ & ce\ast j-cf\ast k-cg+ch\ast i+\\ & dek+df\ast j-dg\ast i-dh\\ =& (ae-bf-cg-dh)+\\ & (be+af-dg+ch)\ast i\\ & (ce+df+ag-bh)\ast j\\ & (de-cf+bg+ah)\ast k\end{array}$$
上面的结果可以写成一个方阵和一个列矩阵相乘：
$$q_1\ast q_2=\left|\begin{array}{cccc}a& -b& -c& -d\\ b& a& -d& c\\ c& d& a& -b\\ d& -c& b& a\end{array}\right|\left|\begin{array}{c}e\\ f\\ g\\ h\end{array}\right|$$
如果矩阵$q_2=1+0\ast i+0\ast j+0\ast k$，则$q_1\ast q_2=q_1$

四元数与旋转的关系

四元数可以表示三维空间中物体的旋转或姿态，从$q=w+x\ast i+y\ast j+z\ast k$很难想象出来，但是如果换成$q=[\cos \frac{\theta }{2},\sin \frac{\theta }{2}\ast \hat{n}]$就好理解多了，这个四元数表示一个绕轴$\hat{n}$旋转$\theta$度的旋转动作。对一个向量（或者坐标系）进行旋转可以表示为$v^{{}^{\prime }}=q^{\ast }vq$。

二、数学模型

为了用陀螺仪数据求出物体的姿态，我们需要将物理原理抽象成数学模型，然后用数学方法求解。假设惯性坐标系位$E$，载体坐标系位$b$，陀螺仪输出的角速度记作${\omega }_{Eb}^b$，物体在惯性坐标系的角速度记作${\omega }_{Eb}^E$，通过坐标系旋转$q$将载体坐标系下的角速度转换为惯性坐标系下的角速度，即$q^{\ast }{\overrightarrow{\omega }}_{Eb}^{b}q={\overrightarrow{\omega }}_{Eb}^E$。只要求出$q$就能知道物体相对的姿态变化情况。

1. 四元数微分方程

令$Q=[\cos \frac{\theta }{2},\hat{n}\sin \frac{\theta }{2}]$，则$Q$对时间$t$的微分方程为：
Q ˙ = − 1 2 sin ⁡ θ 2 d θ d t + d n ^ d t sin ⁡ θ 2 + 1 2 n ^ cos ⁡ θ 2 d θ d t = 1 2 d θ d t ( cos ⁡ θ 2 n ^ − sin ⁡ θ 2 ) , because  d n ^ d t = 0 = 1 2 n ^ d θ d t ( cos ⁡ θ 2 + n ^ sin ⁡ θ 2 ) , because  n ^ ∗ n ^ = − 1 = 1 2 n ^ ω → E b E ( cos ⁡ θ 2 + n ^ sin ⁡ θ 2 ) = 1 2 n ^ ω → E b E Q = 1 2 n ^ Q ω → E b b , because  ω → E b b = Q ∗ ω → E b E Q , Q ∗ Q = 1 = 1 2 ( q 0 + q 1 i + q 2 j + q 3 k ) ( 0 + ω x i + ω y i + ω z k )

$$\begin{aligned} \dot{Q} & = - \frac{1}{2}\sin{\frac{\theta}{2}} \frac{ {\rm d}\theta}{ {\rm d}t} + \frac{ {\rm d}\hat{n}}{ {\rm d}t} \sin{\frac{\theta}{2}} + \frac{1}{2}\hat{n}\cos{\frac{\theta}{2}}\frac{ {\rm d}\theta}{ {\rm d}t} \\ & = \frac{1}{2}\frac{ {\rm d}\theta}{ {\rm d}t}(\cos{\frac{\theta}{2}}\hat{n}-\sin{\frac{\theta}{2}}),& \text{because }\frac{ {\rm d}\hat{n}}{ {\rm d}t}=0 \\ & = \frac{1}{2}\hat{n}\frac{ {\rm d}\theta}{ {\rm d}t}(\cos{\frac{\theta}{2}}+\hat{n}\sin{\frac{\theta}{2}}), &\text{because }\hat{n}\ast\hat{n}=-1 \\ & = \frac{1}{2}\hat{n}\overrightarrow\omega_{Eb}^{E}(\cos{\frac{\theta}{2}}+\hat{n}\sin{\frac{\theta}{2}}) \\ & = \frac{1}{2}\hat{n}\overrightarrow\omega_{Eb}^{E}Q \\ & = \frac{1}{2}\hat{n}Q\overrightarrow\omega_{Eb}^{b}, & \text{because }\overrightarrow\omega_{Eb}^{b}=Q^{\ast}\overrightarrow\omega_{Eb}^{E}Q,Q^{\ast}Q=1 \\ & = \frac{1}{2}(q_0+q_1i+q_2j+q_3k)(0+\omega_xi+\omega_yi+\omega_zk) \end{aligned}$$ Q˙​​=−21​sin2θ​dtdθ​+dtdn^​sin2θ​+21​n^cos2θ​dtdθ​=21​dtdθ​(cos2θ​n^−sin2θ​),=21​n^dtdθ​(cos2θ​+n^sin2θ​),=21​n^ω EbE​(cos2θ​+n^sin2θ​)=21​n^ω EbE​Q=21​n^Qω Ebb​,=21​(q0​+q1​i+q2​j+q3​k)(0+ωx​i+ωy​i+ωz​k)​because dtdn^​=0because n^∗n^=−1because ω Ebb​=Q∗ω EbE​Q,Q∗Q=1​

2. 四元数微分方程的矩阵形式

根据两个四元数相乘的矩阵形式，上式改写为：
Q ˙ = 1 2 ∣ q 0 − q 1 − q 2 − q 3 q 1 q 0 − q 3 q 2 q 2 q 3 q 0 − q 3 q 3 − q 2 q 1 q 0 ∣ ∣ 0 ω x ω y ω z ∣ = 1 2 ∣ 0 − ω x − ω y − ω z ω x 0 − ω z − ω y ω y − ω z 0 ω x ω z ω y − ω x 0 ∣ ∣ q 0 q 1 q 2 q 3 ∣

$$\begin{aligned} \dot{Q} = & \frac{1}{2}\begin{vmatrix}q_0&-q_1&-q_2&-q_3\\q_1&q_0&-q_3&q_2\\q_2&q_3&q_0&-q_3\\q_3&-q_2&q_1&q_0\end{vmatrix} \begin{vmatrix}0\\\omega_x\\\omega_y\\\omega_z\end{vmatrix} \\ = & \frac{1}{2}\begin{vmatrix}0&-\omega_x&-\omega_y&-\omega_z\\\omega_x&0&-\omega_z&-\omega_y\\\omega_y&-\omega_z&0&\omega_x\\\omega_z&\omega_y&-\omega_x&0\end{vmatrix}\begin{vmatrix}q_0\\q_1\\q_2\\q_3\end{vmatrix} \end{aligned}$$ Q˙​==​21​∣∣∣∣∣∣∣∣​q0​q1​q2​q3​​−q1​q0​q3​−q2​​−q2​−q3​q0​q1​​−q3​q2​−q3​q0​​∣∣∣∣∣∣∣∣​∣∣∣∣∣∣∣∣​0ωx​ωy​ωz​​∣∣∣∣∣∣∣∣​21​∣∣∣∣∣∣∣∣​0ωx​ωy​ωz​​−ωx​0−ωz​ωy​​−ωy​−ωz​0−ωx​​−ωz​−ωy​ωx​0​∣∣∣∣∣∣∣∣​∣∣∣∣∣∣∣∣​q0​q1​q2​q3​​∣∣∣∣∣∣∣∣​​

三、常微分方程的初值问题

工程上很多问题建成数学模型时都是微分方程的形式，而ordinary differential equation（ODE），即常微分方程是微分方程中较为简单的一类，常微分方程初值问题则是常微分方程理论研究和实际应用的一种基本定解问题，可以描述为以下形式：
{ y ′ = f ( t , y ) y ( 0 ) = y 0 t ∈ [ a , b ]

$$\begin{cases} y^{'}=f(t,y) \\ y(0)=y_0 \\ t\in{[a,b]} \end{cases}$$ ⎩⎪⎨⎪⎧​y′=f(t,y)y(0)=y0​t∈[a,b]​
直接求解常微分方程难度较大，所以伟大的数学家们想出了各种近似求法，能够在一定误差范围内求出方程（组）的解。粗略来说，这些近似求解法的基本思想是已知上一个值求下一个值，下一个值等于上一个值加上一个增量，而增量约等于步长乘以斜率。本文讲到的求解方法基本上都是在“斜率”上做文章，也有在步长上改进算法的，如“可变步长法”。

1. 欧拉法

欧拉法是很多求解方法的基础，它表示为：
{ ω 0 = y 0 ω i + 1 = ω i + h f ( t i , ω i )

$$\begin{cases} \omega_0=y_0 \\ \omega_{i+1}=\omega_i+hf(t_i,\omega_i) \end{cases}$$ {ω0​=y0​ωi+1​=ωi​+hf(ti​,ωi​)​
其中$y_0$为初值，$h$为时间$t$轴上的步长，$f(t_i,{\omega }_i)$为该点的斜率。从${\omega }_0$开始不断迭代就能够求出点$t_i$处的近似解${\omega }_i$。
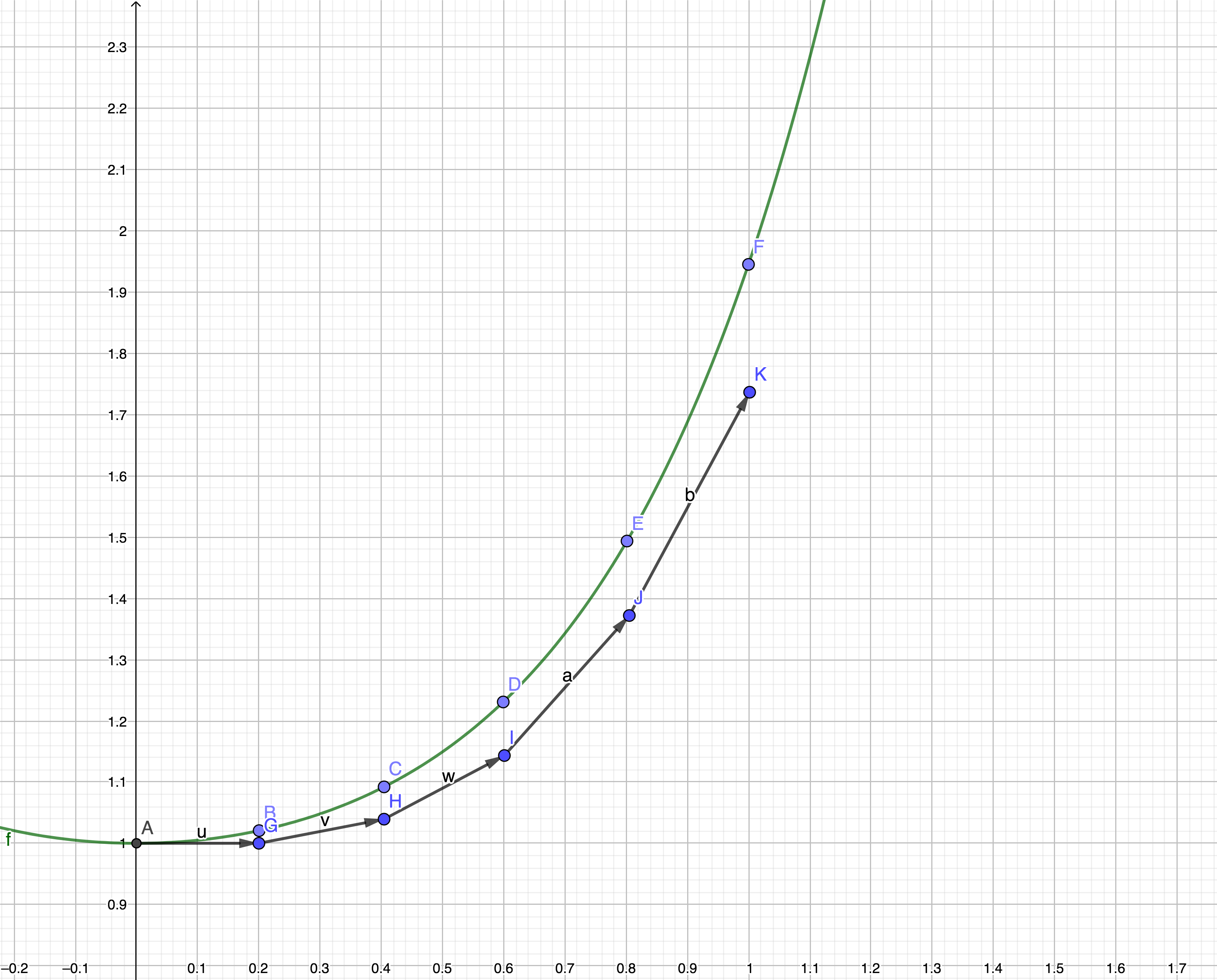
以下函数为例：$$f(x)=3e^{\frac{x^2}{2}}-x^2-2$$。初值为0，步进值为0.2，使用欧拉法，取区间左端点斜率为变化方向。由图中可以看到绿色的线是真实值的曲线，而黑色的线是估计值的曲线。估计值和真实值之间存在一定的误差。如果我们把步进值改成0.1甚至更小，那么估计值就会越靠近真实值，不过也因此会带来更大的计算量。

2. 显式梯形法

对于常微分方程求解法，工程上一般需要考虑截断误差、时间复杂度和空间复杂度（在后续文章中介绍），综合这些指标选择最合适的算法。欧拉法能够求出近似解，而且计算量比较小，但是误差比较大。显式梯形法是对欧拉法的一种改进，它由以下公式推导：
{ ω 0 = y 0 ω i + 1 = ω i + h f ( t i , ω i ) ω i + 1 = ω i + h f ( t i + h , ω i + 1 ) = ω i + h f ( t i + h , ω i + h f ( t i , ω i ) )

$$\begin{cases} \omega_0=y_0 \\ \omega_{i+1}=\omega_{i}+hf(t_i,\omega_i) \\ \omega_{i+1}=\omega_{i}+hf(t_i+h,\omega_{i+1})=\omega_{i}+hf(t_i+h,\omega_i+hf(t_i,\omega_i)) \end{cases}$$ ⎩⎪⎨⎪⎧​ω0​=y0​ωi+1​=ωi​+hf(ti​,ωi​)ωi+1​=ωi​+hf(ti​+h,ωi+1​)=ωi​+hf(ti​+h,ωi​+hf(ti​,ωi​))​
将上面两个式子相加除以二则可以得到下列式子，即显式梯形法：
$$\{\begin{array}{l}{\omega }_0=y_0\\ {\omega }_{i+1}={\omega }_i+\frac{h}{2}(f(t_i,{\omega }_i)+f(t_i+h,{\omega }_i+hf(t_i,{\omega }_i)))\end{array}$$
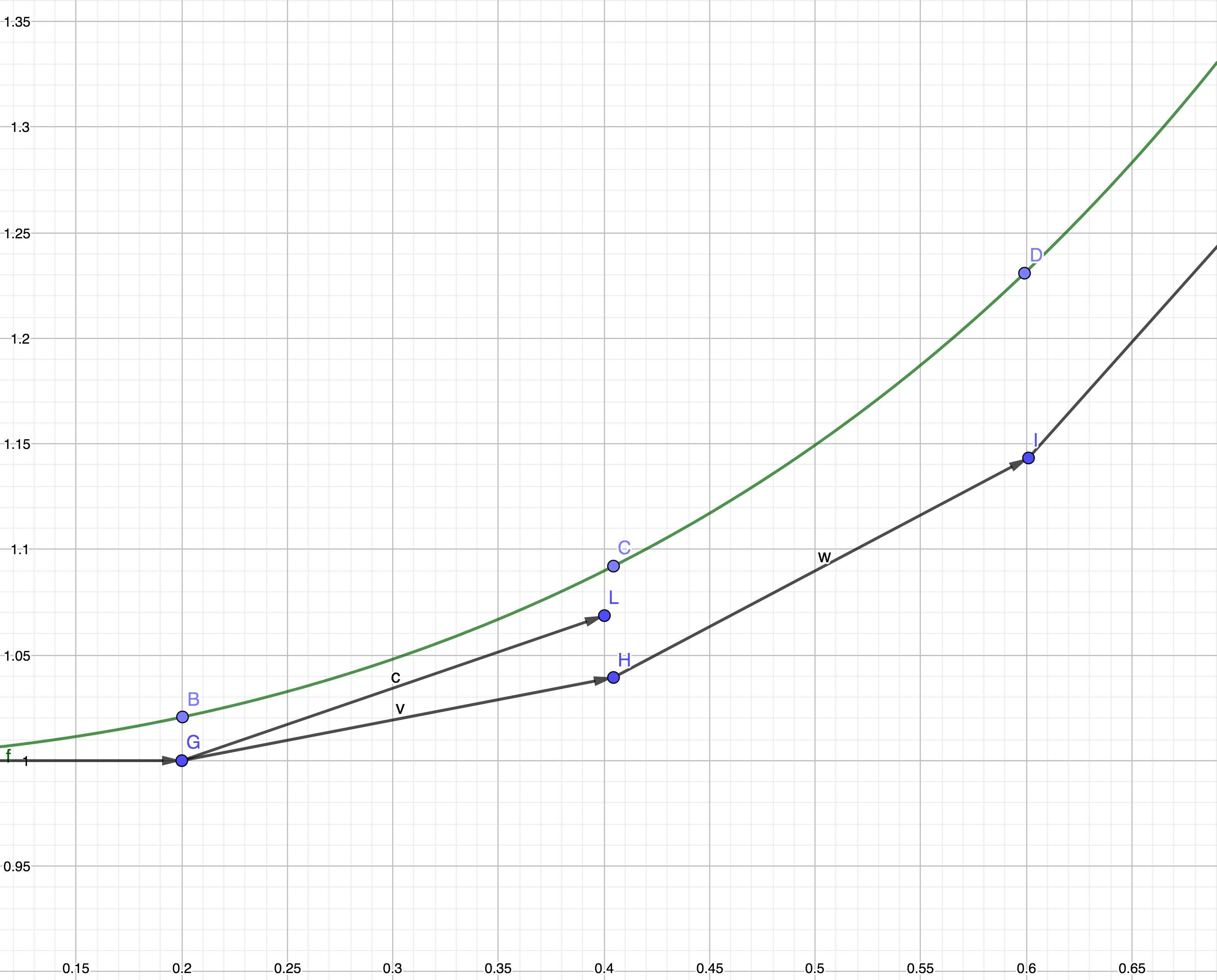
显式梯形法使用了两次欧拉法，用区间左端点和区间右端点斜率的均值当步进方向，相比于欧拉法，显式梯形法提高了精度，但增加了一倍计算量。
如下图所示，在计算$t=0.4$对应的估计值$C^{{}^{\prime }}$时，欧拉法区间左端点斜率可以用向量$\overrightarrow{v}$表示，区间右端点斜率可以用向量$\overrightarrow{w}$表示，两者的均值向量$\overrightarrow{c}$就是显式梯形法的斜率。可以直观地看出显式梯形法估计出来的值会比欧拉法更靠近真实值。事实上也是如此，欧拉法是一种一阶方法，而显式梯形法是一种二阶方法，精度比欧拉法高。

3. 中点法

中点法也是欧拉法的一种改进方法，顾名思义，中点法采用了区间中点的斜率为步进方向，它表示为：
{ ω 0 = y 0 ω i + 1 = ω i + h f ( t i + h 2 , f ( t i , ω i + h 2 f ( t i , ω i ) ) )

$$\begin{cases} \omega_0=y_0 \\ \omega_{i+1}=\omega_i+hf(t_i+\frac{h}{2},f(t_i, \omega_i+\frac{h}{2}f(t_i,\omega_i))) \end{cases}$$ {ω0​=y0​ωi+1​=ωi​+hf(ti​+2h​,f(ti​,ωi​+2h​f(ti​,ωi​)))​
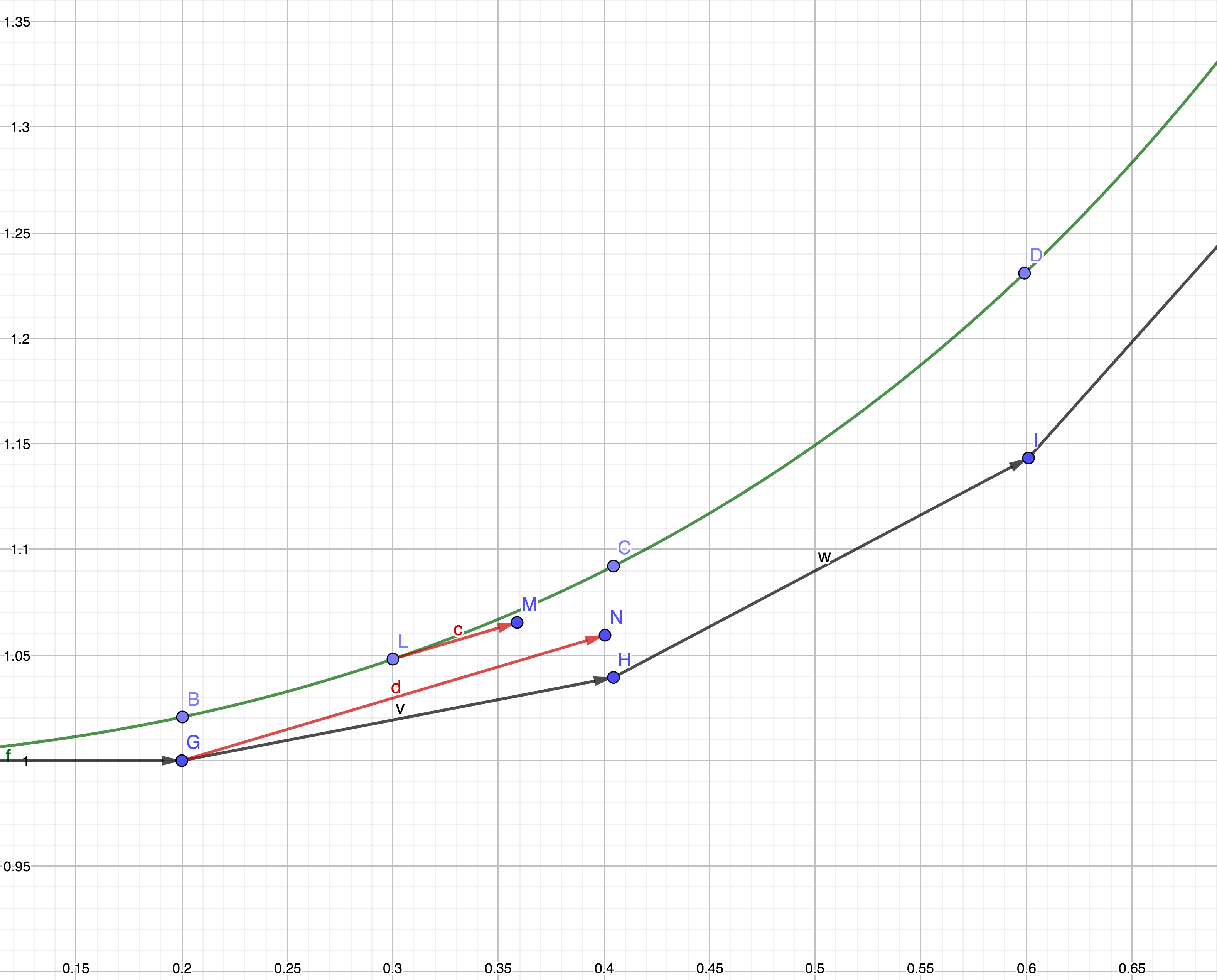
如下图所示，向量$\overrightarrow{c}$是区间中点的斜率，向量$\overrightarrow{d}$与$\overrightarrow{c}$平行，向量$\overrightarrow{d}$明显比向量$\overrightarrow{v}$更靠近点$C$的真实值。中点法跟显式梯形法一样是一种二阶方法，比欧拉法的精度更高一些。

4. 泰勒法

高等数学学过泰勒展开式，如果一个函数$y(t)$是一个$k+1$阶连续可微的函数，那么对于给定的点$(t,y(t))$处，在区间$[t,t+h]$可以进行泰勒展开得到：
$$y(t+h)=y(t)+hy(t{)}^{{}^{\prime }}+\frac{h^2}{2}y(t{)}^{{}^{\prime \prime }}+\cdots +\frac{h^k}{k!}{y}^{(k)}(t)+\frac{h^{k+1}}{(k+1)!}{y}^{(k+1)}(c)$$
最后一项为余项，$c\in (t,t+h)$。由此引申出k阶泰勒法如下：
{ ω 0 = y 0 ω i + 1 = ω i + h f ( t i , ω i ) + h 2 2 f ′ ( t i , ω i ) + ⋯ + h k k ! f ( k − 1 ) ( t i , ω i )

$$\begin{cases} \omega_{0}=y_0 \\ \omega_{i+1}=\omega_{i}+hf(t_i,\omega_i)+\frac{h^2}{2}f^{'}(t_{i},\omega_{i})+\cdots+\frac{h^k}{k!}f^{(k-1)}(t_i,\omega_i) \end{cases}$$ {ω0​=y0​ωi+1​=ωi​+hf(ti​,ωi​)+2h2​f′(ti​,ωi​)+⋯+k!hk​f(k−1)(ti​,ωi​)​
其中，$f(t_i,{\omega }_i)$表示关于$t$的全导数。注意到，欧拉法是泰勒法取前两项的结果。
从泰勒法我们可以看出，理论上可以推出任意阶（$y(t)$可微）的求解常微分方程的方法，不过因为泰勒法需要求解全导数，计算量相对较大，所以泰勒法在实际应用中较少出现。

5. 龙格库塔法

龙格库塔法（Runge-Kutta，简称RK法）是一组常微分方程求解器，它可以根据要求调整阶数，输出误差级别不一样的结果。龙格库塔法的基本思想囊括了以上讲到的欧拉法、显式梯形法、中点法和泰勒法，是一种使用广泛的求解方法。

龙格库塔法的一般形式

泰勒法理论上可以求出任意阶的结果，但是因为求解高阶导数非常麻烦，龙格库塔法通过在区间内取多个点的斜率，然后进行线性组合，从而得到不用计算高阶导数的n阶方法。它的一般形式如下：
{ ω 0 = y 0 ω i + 1 = ω i + h ∑ i = 1 L λ i K i K 1 = f ( x i , ω i ) K i = f ( x n + c i h , ω i + c i h ∑ j = 1 i − 1 a i j K j ) , i = 2 , 3 ⋯   , L

$$\begin{cases} \omega_0=y_0 \\ \omega_{i+1}=\omega_i+h\sum_{i=1}^{L}\lambda_iK_i \\ K_1=f(x_i,\omega_i) \\ K_i=f(x_n+c_ih,\omega_i+c_ih\sum_{j=1}^{i-1}a_{ij}K_j),i=2,3\cdots,L \end{cases}$$ ⎩⎪⎪⎪⎨⎪⎪⎪⎧​ω0​=y0​ωi+1​=ωi​+h∑i=1L​λi​Ki​K1​=f(xi​,ωi​)Ki​=f(xn​+ci​h,ωi​+ci​h∑j=1i−1​aij​Kj​),i=2,3⋯,L​
其中，$c_i\le 1$，${\sum }_{i=1}^L{\lambda }_i=1$，${\sum }_{j=1}^{i-1}{a}_{ij}=1$。
上文提到的中点法是一种二阶龙格库塔法。

四阶龙格库塔法

四阶龙格库塔法是最经典的龙格库塔法，它的截断误差、时间复杂度和空间复杂度都非常适合在工程上应用，常用于工程上求解常微分方程问题，它的形式为：
{ ω 0 = y 0 ω i + 1 = ω i + h 6 ( s 1 + 2 s 2 + 2 s 3 + s 4 ) s 1 = f ( t i , ω i ) s 2 = f ( t i + 1 2 h , ω i + h 2 s 1 ) s 3 = f ( t i + 1 2 h , ω i + h 2 s 2 ) s 4 = f ( t i + h , ω i + h s 3 )

$$\begin{cases} \omega_0=y_0 \\ \omega_{i+1}=\omega_i+\frac{h}{6}(s_1+2s_2+2s_3+s_4) \\ s_1=f(t_i,\omega_i) \\ s_2=f(t_i+\frac{1}{2}h,\omega_i+\frac{h}{2}s_1) \\ s_3=f(t_i+\frac{1}{2}h,\omega_i+\frac{h}{2}s_2) \\ s_4=f(t_i+h,\omega_i+hs_3) \end{cases}$$ ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧​ω0​=y0​ωi+1​=ωi​+6h​(s1​+2s2​+2s3​+s4​)s1​=f(ti​,ωi​)s2​=f(ti​+21​h,ωi​+2h​s1​)s3​=f(ti​+21​h,ωi​+2h​s2​)s4​=f(ti​+h,ωi​+hs3​)​
通过上式可以看到四阶龙格库塔法用到了四个斜率，分别是区间左端点斜率，区间中点斜率，近似的区间中点斜率以及近似的区间右端点斜率，并给了四个斜率不同的权重。龙格库塔法通过这种对区间中多个斜率的线性组合的方式，使得求解出来的估计值比欧拉法、显式梯形法和中点法更加接近真实值，而且虽然龙格库塔法需要进行四次函数计算，但是不需要求解高阶导数。

四、龙格库塔法求解四元数微分方程

我们已经知道四元数表示的微分方程：
Q ˙ = 1 2 ∣ 0 − ω x − ω y − ω z ω x 0 − ω z − ω y ω y − ω z 0 ω x ω z ω y − ω x 0 ∣ ∣ q 0 q 1 q 2 q 3 ∣ ， \dot{Q} = \frac{1}{2}

$$\begin{vmatrix}0&-\omega_x&-\omega_y&-\omega_z\\\omega_x&0&-\omega_z&-\omega_y\\\omega_y&-\omega_z&0&\omega_x\\\omega_z&\omega_y&-\omega_x&0\end{vmatrix}$$ $$\begin{vmatrix}q_0\\q_1\\q_2\\q_3\end{vmatrix}$$ ， Q˙​=21​∣∣∣∣∣∣∣∣​0ωx​ωy​ωz​​−ωx​0−ωz​ωy​​−ωy​−ωz​0−ωx​​−ωz​−ωy​ωx​0​∣∣∣∣∣∣∣∣​∣∣∣∣∣∣∣∣​q0​q1​q2​q3​​∣∣∣∣∣∣∣∣​，
同时也知道了四阶龙格库塔法的公式，那么就可以将四元数微分方程带入四阶龙格库塔公式进行求解。需要注意的是初值条件，一般会设初始角度$\theta$为0，则$Q_0=\left|\begin{array}{cccc}1& 0& 0& 0\end{array}\right|$。具体求解过程如下：
$q_i$为$i$时刻的四元数，${\Omega }_i$为$i$时刻的角速度矩阵，$\Delta t$为时间间隔，则：
$$s_1=\dot{Q_i}=\frac{1}{2}{\Omega }_i{q}_i=\frac{1}{2}\left|\begin{array}{cccc}0& -{\omega }_{xi}& -{\omega }_{yi}& -{\omega }_{zi}\\ {\omega }_{xi}& 0& -{\omega }_{zi}& -{\omega }_{yi}\\ {\omega }_{yi}& -{\omega }_{zi}& 0& {\omega }_{xi}\\ {\omega }_{zi}& {\omega }_{yi}& -{\omega }_{xi}& 0\end{array}\right|\left|\begin{array}{c}{q}_0\\ q_1\\ q_2\\ q_3\end{array}\right|$$
$$s_2=\frac{1}{2}{\Omega }_{i+\frac{1}{2}\Delta t}(q_i+\frac{\Delta t}{2}{s}_1)=\frac{1}{2}\left|\begin{array}{cccc}0& \frac{-({\omega }_{xi}+{\omega }_{xi+1})}{2}& \frac{-({\omega }_{yi}+{\omega }_{yi+1})}{2}& \frac{-({\omega }_{zi}+{\omega }_{zi+1})}{2}\\ \frac{{\omega }_{xi}+{\omega }_{xi+1}}{2}& 0& \frac{-({\omega }_{zi}+{\omega }_{zi+1})}{2}& \frac{-({\omega }_{yi}+{\omega }_{yi+1})}{2}\\ \frac{{\omega }_{yi}+{\omega }_{yi+1}}{2}& \frac{-({\omega }_{zi}+{\omega }_{zi+1})}{2}& 0& \frac{{\omega }_{xi}+{\omega }_{xi+1}}{2}\\ \frac{{\omega }_{zi}+{\omega }_{zi+1}}{2}& \frac{{\omega }_{yi}+{\omega }_{yi+1}}{2}& \frac{-({\omega }_{xi}+{\omega }_{xi+1})}{2}& 0\end{array}\right|\left|\begin{array}{c}{q}_0+\frac{1}{2}\Delta t{s}_1\\ q_1+\frac{1}{2}\Delta t{s}_1\\ q_2+\frac{1}{2}\Delta t{s}_1\\ q_3+\frac{1}{2}\Delta t{s}_1\end{array}\right|$$
$$s_3=\frac{1}{2}{\Omega }_{i+\frac{1}{2}\Delta t}(q_i+\frac{\Delta t}{2}{s}_2)=\frac{1}{2}\left|\begin{array}{cccc}0& \frac{-({\omega }_{xi}+{\omega }_{xi+1})}{2}& \frac{-({\omega }_{yi}+{\omega }_{yi+1})}{2}& \frac{-({\omega }_{zi}+{\omega }_{zi+1})}{2}\\ \frac{{\omega }_{xi}+{\omega }_{xi+1}}{2}& 0& \frac{-({\omega }_{zi}+{\omega }_{zi+1})}{2}& \frac{-({\omega }_{yi}+{\omega }_{yi+1})}{2}\\ \frac{{\omega }_{yi}+{\omega }_{yi+1}}{2}& \frac{-({\omega }_{zi}+{\omega }_{zi+1})}{2}& 0& \frac{{\omega }_{xi}+{\omega }_{xi+1}}{2}\\ \frac{{\omega }_{zi}+{\omega }_{zi+1}}{2}& \frac{{\omega }_{yi}+{\omega }_{yi+1}}{2}& \frac{-({\omega }_{xi}+{\omega }_{xi+1})}{2}& 0\end{array}\right|\left|\begin{array}{c}{q}_0+\frac{1}{2}\Delta t{s}_2\\ q_1+\frac{1}{2}\Delta t{s}_2\\ q_2+\frac{1}{2}\Delta t{s}_2\\ q_3+\frac{1}{2}\Delta t{s}_2\end{array}\right|$$
$$s_4=\frac{1}{2}{\Omega }_{i+\Delta t}(q_i+\Delta t{s}_3)=\frac{1}{2}\left|\begin{array}{cccc}0& -{\omega }_{xi+1}& -{\omega }_{yi+1}& -{\omega }_{zi+1}\\ {\omega }_{xi+1}& 0& -{\omega }_{zi+1}& -{\omega }_{yi+1}\\ {\omega }_{yi+1}& -{\omega }_{zi+1}& 0& {\omega }_{xi+1}\\ {\omega }_{zi+1}& {\omega }_{yi+1}& -{\omega }_{xi+1}& 0\end{array}\right|\left|\begin{array}{c}{q}_0+\Delta t{s}_3\\ q_1+\Delta t{s}_3\\ q_2+\Delta t{s}_3\\ q_3+\Delta t{s}_3\end{array}\right|$$
$$Q_{i+1}=Q_i+\frac{h}{6}(s_1+2s_2+2s_3+s_4)$$
通过以上方法不断迭代就能求出$i$时刻的四元数。

五、四元数转欧拉角

以上求解可以得到一个表示$i$时刻旋转状态的四元数$Q_i$，再通过四元数和欧拉角的转换关系即可得到物体旋转后的姿态。
欧拉角和四元数没有直接的转换关系，需要先转换成旋转矩阵。而且欧拉角的表示跟坐标系的选择和旋转顺序有关，具体在其他文章详细介绍。