基于深度强化学习的路径规划笔记_基于强化学习的路径规划

感谢知乎搬砖的旺财博主；此方法同源借鉴于ICIA一篇强化学习paper
源码github地址：https://github.com/a7b23/Autonomous-MazePathFinder-using-DQN

该程序将由几个封锁（由块颜色表示）组成的图像作为输入，起始点由蓝色表示，目的地由绿色表示。 它输出一个由输入到输出的可能路径之一组成的图像。 下面显示的是程序的输入和输出。

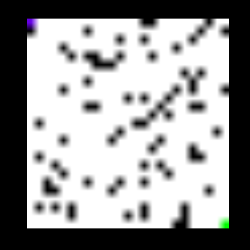
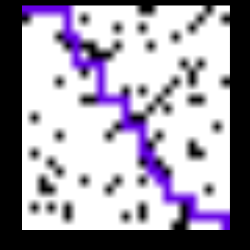
输入图像被馈送到由2个conv和2个fc层组成的模型，其输出对应于底部和右侧动作的Q值。 代理根据哪个Q值更大而向右或向下移动，并且使用代理的新位置生成的相应新图像再次被馈送到模型。获得输出状态并反馈新图像的过程保持重复 直到代理到达到达目的地的终端阶段。

总体思路：

• 获取image（map）
• Agent处理image
• Mobile Robot得到向前还是向右的指令
• 实现了对无人车end-to-end的路径规划。

Data Generation

代码DataGeneration.py为任务生成必需的数据。 它在25X25大小的图像中随机分配1X1像素大小的块。同时生成对应于每个不同起始位置的所有625个图像并将其存储在文件夹中。具有变化的阻塞位置的200个不同的这样的游戏的图像是 生成，因此总训练图像达250 * 625。 还生成与每个不同状态（图像）相关联的分数并将其存储在txt文件中，其中起始点与阻塞碰撞的状态获得-100的分数，当起始点与目的地碰撞时，其获得分数 100和所有剩余的状态得分为0。

Training

InitialisingTarget.py生成与每个训练图像相关联的初始Q值，并将它们存储在txt文件-Targets200_New.txt中。生成的Q值只不过是随机初始化模型的输出。 training2.py开始训练模型。从trainig数据中选择随机批量大小的图像集并将其馈送到模型。根据损失更新模型权重，该损失是输出Q值和预期Q值之间的平方差异。预期的Q（s，a）= r（s，a）+ gamma * max（Q1（s1，a）），其中max取2个动作。这里Q1对应于存储在’Targets200_New.txt’文件中的q值。奖励r也是下一个州和当前州之间得分的差异。几个训练Q1值的时期再次更新并存储在相同的txt文件中，输出来自训练模型。新的Q1值再次用于训练模型。生成目标Q值和训练模型的步骤重复几个步骤，直到模型学习所需特征。

Testing

就像DataGeneration.py一样，TestDataCollection.py也以相同的格式生成图像，除了它不是200个游戏，而是在单独的文件夹中生成仅对应20个游戏的图像。 对于20个游戏中的每个游戏，testing.py获取对应于代理位于0,0位置的图像，并将单个最终路径的图像输出到单独的文件夹中的目的地。 对于由于与阻塞冲突而无法找到路径的游戏，不会生成图像。

initialisingtarget.py生成每个训练图像对应的初始Q值，保存在TXT文件targets200_new中，产生的Q值只是随机初始化模型的输出。

一、定义函数

定义一个函数，用于初始化所有的权值W

def weight_variable(shape):
    initial = tf.truncated_normal(shape, stddev=0.05)
    return tf.Variable(initial)
1
2
3

定义一个函数，用于初始化所有的偏置项b

def bias_variable(shape):
    initial = tf.constant(0.05, shape=shape)
    return tf.Variable(initial)
1
2
3

定义一个函数，用于构建卷积层

def conv2d(x, W):
    return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')
1
2

x为input，[batch, in_height, in_width, in_channels] ，[训练时一个batch的图片数量, 图片高度, 图片宽度, 图像通道数]；
W为卷积核，它要求是一个Tensor，[filter_height, filter_width, in_channels, out_channels]，[卷积核的高度，卷积核的宽度，图像通道数，卷积核个数]，要求类型与参数input 相同，有一个地方需要注意，第三维 in_channels，就是参数input的第四维；
strides，卷积时在图像每一维的步长；
padding：string 类型的量，只能是"SAME" , “VALID” 其中之一，这个值决定了不同的卷积方式。

二、网络

2.1 input layer

x = tf.placeholder(tf.float32, shape=[None, imageSize[0], imageSize[1], imageSize[2]])
1

shape=[None, imageSize[0], imageSize[1], imageSize[2]]
shape转换成了4D tensor，第二与第三维度对应的是照片的宽度与高度，最后一个维度是颜色通道数
2. tf.placeholder(dtype, shape=None, name=None)

dtype：数据类型。常用的是tf.float32 , tf.float64 等数值类型；
shape：数据形状。默认是None，就是一维值，也可以是多维，比如[2,3] , [None, 3] 表示列是3，行不定；
name：名称。

2.2 卷积层

2.2.1 卷积神经网络之训练算法

同一般机器学习算法，先定义Loss function，衡量和实际结果之间差距
找到最小化损失函数的w和b，CNN中用的算法是SGD（随机梯度下降）
卷积运算是为了提取输入的不同特征，第一层可能只能提取到一些简单的特征，例如边缘，层数越高提取的特征越复杂。

卷积层有两个关键操作:

局部关联。每个神经元看做一个滤波器(filter)
窗口(receptive field)滑动，filter对局部数据计算

由于卷积层的神经元也是三维的，所以也具有深度
卷积层的参数包含一系列过滤器，每个过滤器训练一个深度，有几个过滤器输出单元就具有多少深度
对于输出单元不同深度的同一位置，与输入图片连接的区域是相同的，但是参数（过滤器）不同

2.2.2 卷积神经网络之优缺点

优点
共享卷积核，对高维数据处理无压力
无需手动选取特征，训练好权重，即得特征分类效果好
2. 缺点
需要调参，需要大样本量，训练最好要GPU
物理含义不明确（也就说，我们并不知道每个卷积层到底提取到的是什么特征，而且神经网络本身就是一种难以解释的“黑箱模型”）

2.2.3 第1个卷积层

如下图所示，展示了一个3×3的卷积核在5×5的图像上做卷积的过程。每个卷积都是一种特征提取方式，就像一个筛子，将图像中符合条件（激活值越大越符合条件）的部分筛选出来。

# network weights
# 第1、2个参数是窗口的大小，第3个参数是channel的数量，第4个参数定义了我们想使用多少个特征
W_conv1 = weight_variable([2, 2, 3, 10])
b_conv1 = bias_variable([10]) 

# hidden layers
h_conv1 = tf.nn.relu(conv2d(x, W_conv1) + b_conv1)
1
2
3
4
5
6
7

分析程序的第一个卷积层，可以发现输入照片大小为25 * 25，窗口为2 * 2，会产生第一层隐藏层中25 * 25排列的神经元，这是因为我们需要从上到下移动窗口25次，从左到右移动窗口25 次来覆盖整个输入图片。在这里是假设窗口每次只移动一个像素，所以新窗口与上次的窗口会有重叠。

padding=‘SAME’
输入矩阵W×W，W = 25；
filter矩阵F×F，卷积核，F = 2；
stride值S，步长，S = 1；
1.计算：

new_height = new_width = W / S = 25 / 1 = 25 #结果向上取整
1

含义：new_height为输出矩阵的高度
说明：对W/S的结果向上取整得到W"包含"多少个S
2. pad_needed_height = (new_height – 1) × S + F - W = （25-1）X 1 + 2 - 25 = 1

含义：pad_needed_height为输入矩阵需要补充的高度
说明：因为new_height是向上取整的结果，所以先-1得到W可以完全包裹住S的块数，之后乘以S得到这些块数的像素点总和，再加上filer的F并减去W，即得到在高度上需要对W补充多少个像素点才能满足new_height的需求
3. pad_top = pad_needed_height / 2 = 1 / 2 = 0 #结果取整

含义：pad_top为输入矩阵上方需要添加的高度
说明：将上一步得到的pad_needed_height除以2 作为矩阵上方需要扩充0的像素点数
4. pad_bottom = pad_needed_height - pad_top = 1 - 0 =1

含义：pad_bottom为输入矩阵下方需要添加的高度
说明：pad_needed_height减去pad_top的剩余部分补充到矩阵下方
同理：

pad_needed_width = (new_width – 1) × S + F - W = （25-1）X 1 + 2 - 25 = 1
pad_left = pad_needed_width / 2 = 0
pad_right = pad_needed_width – pad_left = 1

基于我们研究的样例，我们需要1个bias b与1个2*2的矩阵W来连接输入层与隐藏层的神经元。

CNN的一个关键特性是这个权重矩阵W与bias b是隐藏层中所有神经元间共享的。

本程序中是24 * 24 (576) 个神经元。你将会发现与全连接的神经网络相比，这会大大减少权重参数的数量。具体来说，由于共享了权重矩阵W，参数数量会从2304(2 * 2 * 24 * 24) 降到4(2 * 2)。

这个共享的矩阵W与bias b在CNN中经常被叫作kernel或filter。这些filters与图像处理程序中润色图片的那些是类似的，此处是用来找出有鉴别性的feature。

一个矩阵与bias定义了一个kernel。一个kernel仅仅只检测图像中一个特定相关的feature，所以建议使用多个kernels，每个想检测的特征一个kernel。这就意味着CNN中一个完整的卷积层包含了很多kernels。描述这些kernels的一个常用方法如下：

隐藏层的第一层包含了多个kernels。此处，我使用了10 个kernels，每一个定义了2*2的权重矩阵W和bias b，这两个参数也是隐藏层间共享的。

ReLU（Rectified Linear unit）激活函数最近变成了神经网络中隐藏层的默认激活函数。这个简单的函数包含了返回max(0,x)，所以对于负值，它会返回0，其它返回x。

代码中首先对输入图像x(image) 计算卷积，计算得到的结果保存在2D tensor W_conv1中，然后与bias求和，接下来应用ReLU激活函数。

2.2.4 第2个卷积层

# network weights
W_conv2 = weight_variable([2, 2, 10, 20])
b_conv2 = bias_variable([20])

# hidden layers
h_conv2 = tf.nn.relu(conv2d(h_conv1, W_conv2) + b_conv2)
1
2
3
4
5
6

分析程序的第二个卷积层，窗口为2 * 2，20个filters，此时我们会需传递10个channels，因为这是前一层的输出结果。

2.2.5 卷积神经网络的时间复杂度分析

2.2.5.1 单个卷积层的时间复杂度

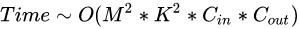
M：每个卷积核输出特征图的边长
K：每个卷积核的边长
C_{in} ：每个卷积核的通道数，也即输入通道数，也即上一层的输出通道数
C_{out} ：本卷积层具有的卷积核个数，也即输出通道数
注：严格来讲每层应该还包含1个Bias参数，这里为了简洁就省略了。


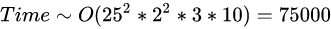
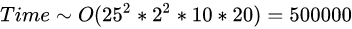
2.2.5.2 卷积神经网络整体的时间复杂度

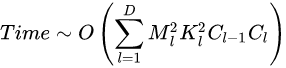
D ：神经网络所具有的卷积层数，也即网络的深度。
l ：神经网络第 l 个卷积层。
C_l ：神经网络第 l 个卷积层的输出通道数 C_{out} ，也即该层的卷积核个数。对于第 l 个卷积层而言，其输入通道数 C_{in} 就是第 l-1 个卷积层的输出通道数。

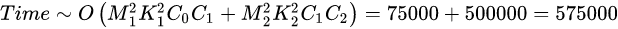
2.2.5.3 时间复杂度对模型的影响
时间复杂度决定了模型的训练/预测时间。如果复杂度过高，则会导致模型训练和预测耗费大量时间，既无法快速的验证想法和改善模型，也无法做到快速的预测。

2.2.6 卷积神经网络的空间复杂度分析

空间复杂度包括模型的参数数量（模型本身的体积）和每层输出的特征图大小（会影响模型运行时的内存占用情况）。

2.2.6.1 空间复杂度

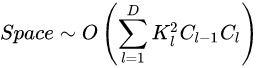
可见，网络的参数量只与卷积核的尺寸K、通道数C、网络的深度D相关。而与输入数据的大小无关。当我们需要裁剪模型时，由于卷积核的尺寸通常已经很小，而网络的深度又与模型的能力紧密相关，不宜过多削减，因此模型裁剪通常最先下手的地方就是通道数。



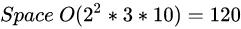
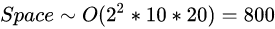
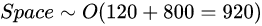
2.2.6.2 空间复杂度对模型的影响
空间复杂度决定了模型的参数数量。由于维度诅咒的限制，模型的参数越多，训练模型所需的数据量就越大，而现实生活中的数据集通常不会太大，这会导致模型的训练更容易过拟合。

2.2.7 神经元的运算

以conv1为例：

卷积核实际上有2X2个神经元，每个神经元的厚度为3，所以1个卷积核有2X2X3个w参数，由于共有10个卷积核，所以共有2X2X3X10个w参数和10个b参数。连接数量为((2X2+1)X10)X25X25=31250。

卷积核输出组成一个25×25的矩阵，称为特征图。

第一个神经元连接到图像的第一个2×2的局部，第二个神经元则连接到第二个局部。（注意，有重叠！就跟你的目光扫视时也是连续扫视一样）如果应用参数共享的话，实际上每一层计算的操作就是输入层和权重的卷积。

下面展示2（输出层的厚度）个3X3X3（卷积核的厚度）的卷积核在7X7X3（输入层的深度）的输入层上做卷积的过程，求出对应输出层的第一个元素（注意有厚度）：




注释： \bullet 代表矩阵做内积。

2.2.8 卷积神经网络的参数共享

给一张输入图片，用一个filter去扫这张图，filter里面的数就叫权重，这张图每个位置是被同样的filter扫的，所以权重是一样的，也就是共享。

对于一张输入图片，大小为WH，如果使用全连接网络，生成一张XY的feature map，需要WHX*Y个参数，如果原图长宽是 10^2 级别的，而且XY大小和WH差不多的话，那么这样一层网络需要的参数个数是 10^8 ~ 10^{12} 级别。

这么多参数肯定是不行的，对于输出层feature map上的每一个像素，他与原图片的每一个像素都有连接，每一个连接都需要一个参数。但注意到图像一般都是局部相关的，那么如果输出层的每一个像素只和输入层图片的一个局部相连，那么需要参数的个数就会大大减少。

假设输出层每个像素只与输入图片上FF的一个小方块有连接，也就是说输出层的这个像素值，只是通过原图的这个FF的小方形中的像素值计算而来，那么对于输出层的每个像素，需要的参数个数就从原来的WH减小到了FF。

如果对于原图片的每一个FF的方框都需要计算这样一个输出值，那么需要的参数只是WHFF，如果原图长宽是 10^2 级别，而F在10以内的话，那么需要的参数的个数只有10^5 ~ 10{6}级别，相比于原来的108 ~ 10^{12}小了很多很多。这还不够。

图片还有另外一个特性：图片的底层特征是与特征在图片中的位置无关的。比如说边缘，无论是在图片中间的边缘特征，还是在图片边角处的边缘特征，都可以用过类似于微分的特称提取器提取。那么对于主要用于提取底层特称的前几层网络，把上述局部全连接层中每一个FF方形对应的权值共享，就可以进一步减少网络中参数的个数。也就是说，输出层的每一个像素，是由输入层对应位置的FF的局部图片，与相同的一组FF的参数（或称权值）做内积，再经过非线性单元计算而来的。这样的话无论图片原大小如何，只用FF个参数就够了，也就是几个几十个的样子。当然一组F*F的参数只能得到一张feature map，一般会有多组参数，分别经过卷积后就可以有好几层feature map。

高级特征一般是与位置有关的，比如一张人脸图片，眼睛和嘴位置不同，那么处理到高层，不同位置就需要用不同的神经网络权重，这时候卷积层就不能胜任了，就需要用局部全连接层和全连接层。

网上找的一张图，示意了局部连接，每一个W只与输入的一部分连接，如果W1和W2是相同的，那么就是卷积层，这时参数W1和W2相同，因此说共享。

2.3 全连接层

全连接层的每一个结点都与上一层的所有结点相连，用来把前边提取到的特征综合起来。在前向计算过程，也就是一个线性的加权求和的过程，全连接层的每一个输出都可以看成前一层的每一个结点乘以一个权重系数W，最后加上一个偏置值b得到。

2.3.1 第1个全连接层

我们使用包含100个神经元的一层来处理整个图片。权重与bias的tensor如下：
network weights
W_fc1 = weight_variable([25 * 25 * 20, 100])
b_fc1 = bias_variable([100])
tensor的第一维度表示第二层卷积层的输出，大小为25*25带有20个filters，第二个参数是层中的神经元数量，我们可自由设置。

那么，全连接层fc1，输入有252520=12500个神经元结点，输出有100个结点，则一共需要252520*100=1250000个权值参数W和100个偏置参数b。


接下来，我们将tensor打平到vector中。通过打平后的vector乘以权重矩阵W_fc1，再加上bias b_fc1，最后应用ReLU激活函数后就能实现

# hidden layers
h_conv2_flat = tf.reshape(h_conv2, [-1, 25 * 25 * 20])
h_fc1 = tf.nn.relu(tf.matmul(h_conv2_flat, W_fc1) + b_fc1)
# tf.matmul(a, b) 将矩阵a乘于矩阵b
1
2
3
4

2.3.2 第2 个全连接层

我们使用包含2个神经元的一层来处理整个图片。权重与bias的tensor如下：

# network weights
W_fc2 = weight_variable([100, 2])
b_fc2 = bias_variable([2])

# Q Value layer
y_out = tf.matmul(h_fc1, W_fc2) + b_fc2
1
2
3
4
5
6

2.4 网络结构

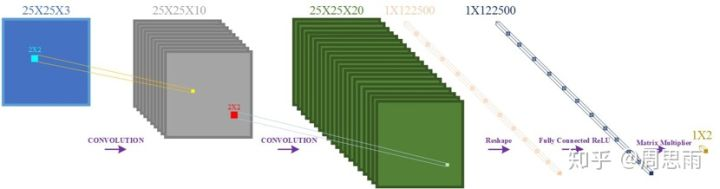
三、读取图像

inputs = np.zeros([totalImages, imageSize[0], imageSize[1], imageSize[2]])
print('reading inputs')
for i in range(totalImages):
    temp = imageSize[0] * imageSize[1]
    inputs[i] = cv2.imread('trainImages/image_' + str(int(i / temp)) + '_' + str(i % temp) + '.png')
print('inputs read')
1
2
3
4
5
6

四、获取Q值

4.1 iterations

imageSize = [25, 25, 3]
batchSize = 100
games = 200
totalImages = games * imageSize[0] * imageSize[1]

iterations = int(totalImages / batchSize)
1
2
3
4
5
6

images一共是25 * 25 * 200 = 125000，然后125000 / 100 = 1250，输出：

number of iterations is 1250
1

4.2 getBatchInput

每次读取一个batchSize的inputs：

batchInput, start = getBatchInput(inputs, start, batchSize) 

def getBatchInput(inputs, start, batchSize):
    first = start
    start = start + batchSize
    end = start
    return inputs[first:end], start
1
2
3
4
5
6
7

4.3 batchOutput

batchOutput = sess.run(y_out, feed_dict={x: batchInput})
1

其中feed_dict也即把batchInput一个一个赋给x，

然后把x feed给我们搭好的网络。

最后把batchOutput赋值给initialTarget：

for j in range(batchSize):
    initialTarget.append(batchOutput[j])
1
2

五、指数衰减

首先使用较大学习率(目的：为快速得到一个比较优的解)；
然后通过迭代逐步减小学习率(目的：为使模型在训练后期更加稳定)。

learningRate = 0.001  # 事先设定的初始学习率；
lr_decay_rate = 0.9  # 衰减系数
lr_decay_step = 2000  # 衰减速度
1
2
3

生成学习率：

lr = tf.train.exponential_decay(learningRate,
  global_step,
  lr_decay_step,
  lr_decay_rate,
  staircase=True)
1
2
3
4
5

每隔lr_decay_step步，learningRate要乘以lr_decay_rate；
staircase = True，每decay_steps次计算学习速率变化，更新原始学习速率。

六、损失函数

loss = tf.reduce_mean(tf.square(y_out), 1)  # tf.reduce_mean(x, 1)指定第二个参数为1，则第二维的元素取平均值，即每一行求平均值

avg_loss = tf.reduce_mean(loss)  # tf.reduce_mean(x)如果不指定第二个参数，那么就在所有的元素中取平均值 
1
2
3

七、训练模型

我们已经定义好模型和训练用的损失函数，那么用TensorFlow进行训练就很简单了。因为TensorFlow知道整个计算图，它可以使用自动微分法找到对于各个变量的损失的梯度值。TensorFlow有大量内置的优化算法。我们用Adam优化算法让avg_loss下降，步长为lr。

train_step = tf.train.AdamOptimizer(lr).minimize(avg_loss)
1

这一行代码实际上是用来往计算图上添加一个新操作，其中包括计算梯度，计算每个参数的步长变化，并且计算出新的参数值。

返回的train_step操作对象，在运行时会使用梯度下降来更新参数。因此，整个模型的训练可以通过反复地运行train_step来完成。

八、运行TensorFlow的InteractiveSession

sess = tf.InteractiveSession()
1

Tensorflow依赖于一个高效的C++后端来进行计算。与后端的这个连接叫做session。一般而言，使用TensorFlow程序的流程是先创建一个图，然后在session中启动它。

这里，我们使用更加方便的InteractiveSession类。通过它，你可以更加灵活地构建你的代码。它能让你在运行图的时候，插入一些计算图，这些计算图是由某些操作(operations)构成的。这对于工作在交互式环境中的人们来说非常便利，比如使用IPython。如果你没有使用InteractiveSession，那么你需要在启动session之前构建整个计算图，然后启动该计算图。

九、记录信息

运行整个程序，在程序中定义的summary node就会将要记录的信息全部保存在指定的logdir 路径中了，训练的记录会存一份文件，测试的记录会存一份文件。

checkpointFile = 'NewCheckpoints/Checkpoint3.ckpt'

saver = tf.train.Saver()  # 生成saver
sess.run(tf.initialize_all_variables())  # 先对模型初始化
1
2
3
4

训练完以后，使用saver.save来保存

sess.run(tf.initialize_all_variables())
1