【二叉树——数据结构】

1.二叉树

1.基本概念.

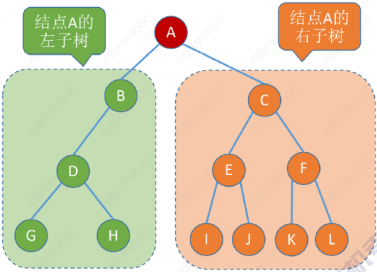
二叉树是n(n>=0)个结点的有限集合
或者为空二叉树，即n=0
或者由一个根结点和两个互不相交的被称作根的左子树和右子树组成。
每个结点至多只有两棵子树
左右子树不能颠倒(二叉树是有序树)
二叉树是递归定义的数据结构
树转化为二叉树:左孩子，右兄弟

几种特殊的二叉树

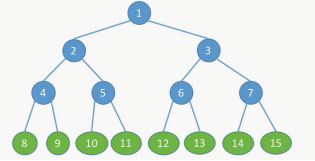
1.满二叉树


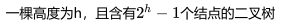
特点

1. 只有最后一层有叶子结点
2. 不存在度为1的结点
3. 按层序从1开始编号，结点i的左孩子为2i,右孩子为2i+1;结点i的父节点为i/2 (如果存在的话)

2.完全二叉树
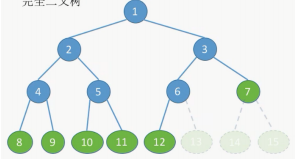当且仅当其每个结点都与高度为h的满二叉树中编号为1-n的结点一-对应, 称为
完全二叉树
特点

1. 只有最后两层可能有叶子结点
2. 最多只有一 个度为1的结点
3. 按层序从1开始编号，结点i的左孩子为2i,右孩子为2i+1;结点i的父节点为[i/2] (如果存在的话)
4. i<=n/2为分支结点，i≥n/2为叶子结点
5. 如果某个节点只有一个孩子， 那这个孩子一定是左孩子

3. 二叉排序树

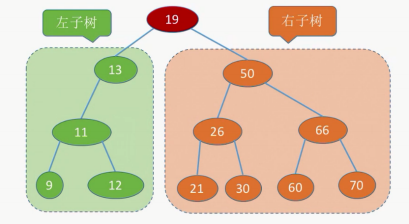
左子树上所有结点的关键字均小于根节点的关键字;右节点上所有结点的关键字均大于根节点的关键字，左子树和右子树又各是一棵二叉排序树。
用于元素的排序，搜索
4.平衡二叉树

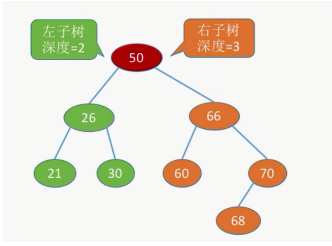
树上任一结点的左子树和右子树的深度之差不超过1
平衡二叉树能有更高的搜索效率

2.考点

1. 设非空二叉树中度为0、1和2的结点个数分别为n0,n1和n2, 则n0 = n2+ 1
   (叶子结点比二分支结点多一个)
2. 二叉树第i层至多有2^(i-1)个结点(i≥1)
3. 高度为h的二叉树至多有2^h - 1个结点(满二叉树)
4. 具有n个(n> 0)个结点的完全二叉树的高度h为[log(n + 1)]或[log n]+1
   编号为i的结点所在层次为[log(i + 1)]或[log i]+1
5. 对于完全二叉树，可以由结点数推出度为0, 1和2的结点个数为n0,n1和n2
6. 若完全二叉树有2k个(偶数)个结点，则必有n1=1， n0=k， n2= k-1
   若完全二叉树有2k-1个(奇数)个结点，则必有n1=0，n0=k， n2= k-1

3.二叉树的存储结构

顺序存储

#define MaxSize 100
struct TreeNode {
	ElemType value; //结点中的数据元素
	bool isEmpty; //结点是否为空
};
TreeNode t [MaxSize] ;
1
2
3
4
5
6

只适合存储完全二叉树

链式存储

//二又树的结点(壁式存储)
typedef struct BiTNode(
	ELemType data;//数据域
	struct BiTNode *lchld,rchild;//左、右孩子指针
}BiTNode,*BTree;
1
2
3
4
5

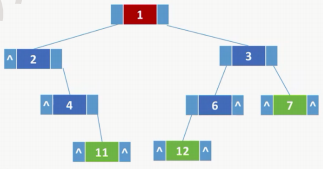
n个结点的二叉链表共有n+ 1个空链域

4.二叉树的遍历

按照某种次序把所有节点都访问一遍

先序遍历——O(n)
根左右
得到前缀表达式

中序遍历——O(n)
左根右
得到中缀表达式(未加界限符)

后序遍历——O(n)
左右根
得到后缀表达式

求树的深度

int treeDepth(BiTree T){
	if (T == NULL) {
		return 0;
	}
	else {
		int 1 = treeDepth(T->lchild);
		int r = treeDepth(T->rchild);
		//树的深度=Max(左子树深度，右子树深度)+1
		return l>r ? 1+1 : r+1;
	}
}
1
2
3
4
5
6
7
8
9
10
11

层次遍历

1. 初始化一个辅助队列
2. 根节点入队
3. 若队列非空,则队头结点出队，访问该结点，并将其左右孩子插入队尾(如果有的话)
4. 重复上一步直至队列为空

//层序遍历
void Levelorder(BiTree T){
	LinkQueue Q;
	InitQueue(Q) ;	//初始化辅助队列
	BiTree p;
	EnQueue(Q,T);	//将根结点入队
	while( !IsEmpty(Q)){	//队列不空则循环
		DeQueue(Q，p);	//队头结点出队
		visit(p);	//访问出队结点
		if(p- >lchild!=NULL)
			EnQueue(Q, p- >lchild); //左孩子入队
		if(p->rchild!=NULL)
			EnQueue(Q,p >rchild); //右孩子入队
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

//二叉树的结点(链式存储)
typedef struct BiTNode{
	char data;
	struct BiTNode *lchild, 电rchild;
}BiTNode, *BiTree;
//链式队列结点
typedef struct LinkNode{
	BiTNode * data;
	struct LinkNode *next;
}LinkNode;
typedef struct{
	LinkNode *front, *rear; //队头队尾
}LinkQueue;
1
2
3
4
5
6
7
8
9
10
11
12
13

由遍历序列构造二叉树
若只给出-一个二叉树的前/中/后/层序遍历队列中的一-种，不能唯- -确定-棵二叉树
前序+中序遍历队列
后序+中序遍历队列
层序+中序遍历队列

前序、后序、层序
序列的两两组合无法唯一
确定一棵二叉树

5.线索二叉树

线索二叉树的作用——方便从一个指定结点出发,找到其前驱、后继;方便遍历线索二叉树的存储结构

//线索二叉树结点
typedef struct ThreadNode{
	ElemType data;
	struct ThreadNode *lchild, *rchild; 
	int ltag, rtag; //左、 右线索标志
}ThreadNode ,*ThreadTree ;
//*Ichild | Itag | data | rtag  |*rchild
//tag==0，表示指针指向孩子
//tag==1，表示指针是"线索"
1
2
3
4
5
6
7
8
9

三种线索二叉树

1. 先序线索二叉树——线索指向、 先序前驱、先序后继
   

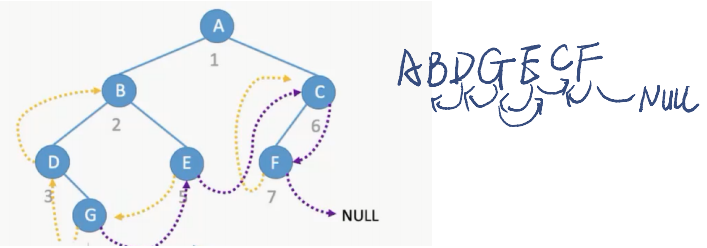
2. 中序线索二叉树——线索指向、中序前驱、中序后继
   

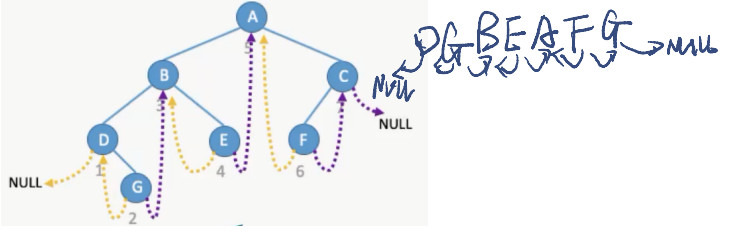
3. 后序线索二叉树——线索指向、后序前驱、后序后继
   
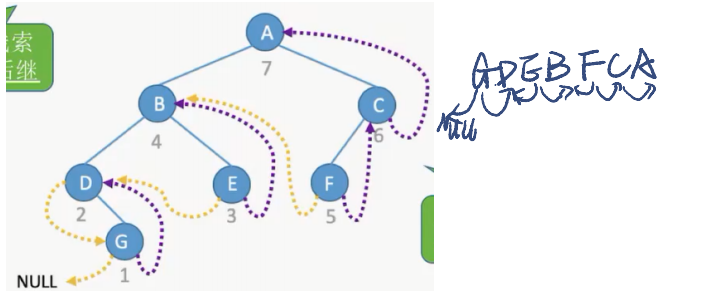
   二叉树的线索化
   中序线索化得到中序线索二叉树
   先序线索化-得到先序线索二叉树
   后序线索化得到后序线索二叉树
   核心
   中序/先序/后序遍历算法的改造，当访问一个结点时，连接该结点与前驱结点的线索信息
   用一个指针pre记录当前访问结点的前驱结点