Nvidia Modulus仿真开发入门

本教程逐步介绍了使用 NVIDIA Modulus 为 Lid Driven Cavity Flow(顶盖驱动方腔流) 生成 2D 流模拟的过程。在本教程中，我们将学习：

1. 如何使用 Modulus 中的几何模块生成 2D 几何。
2. 如何设置边界条件。
3. 如何选择要求解的流动方程。
4. 如何解释不同的损失和调整网络。
5. 如何使用 Modulus 进行一些基本的后处理。

1、问题背景

该问题的几何结构如图 所示。几何体的所有边界都是静止的壁，顶壁在 x 方向上以 1 m/s的速度移动. 基于空腔高度的雷诺数（Reynold Number）选择为 10。

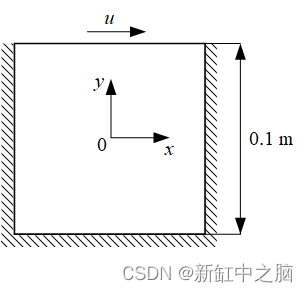
总结关键概念（我们将在下面的理论部分深入讨论）以及它与 Modulus 特征的关系很有帮助。求解任何由微分方程定义的物理仿真，我们都需要有关问题域及其控制方程/边界条件的信息。有了这些数据，就可以使用求解器求解问题域上的方程以获得解。在 Modulus 中，对问题定义、解决方案、监控和后处理的每个阶段都提供了一些模块/功能来支持。可以使用 Modulus 的构造实体几何 (CSG) 模块、STL 模块或来自外部源（如 CSV/numpy/HDF5DataFile 等）的任何一般数据来定义域。对于 PINN（物理信息神经网络），一旦我们有了这个几何/点云，就可以对边界上的点进行二次采样以满足边界条件；也可以利用内部区域以最小化 PDE/ODE 残差。

从 v22.03 开始​​，Modulus 将支持 新的API 和架构，以仅使用数据、仅物理和两者的混合来解决问题。Modulus 现在还使用 PyTorch 作为后端框架（发行说明）。用于生成神经网络、生成和采样几何图形的主要 API 保持不变，但是这些东西组合在一起以解决问题的方式发生了变化。

我们将使用完全物理驱动的方法解决了盖子驱动的腔体流动问题。

2、创建PDE/神经网络节点

在添加任何代码之前，让我们导入创建几何体、网络和绘制结果所需的包：

from sympy import Symbol, Eq, Abs

import modulus
from modulus.hydra import to_absolute_path, to_yaml, instantiate_arch
from modulus.hydra.config import ModulusConfig
from modulus.csv_utils.csv_rw import csv_to_dict
from modulus.continuous.solvers.solver import Solver
from modulus.continuous.domain.domain import Domain
from modulus.geometry.csg.csg_2d import Rectangle

from modulus.continuous.constraints.constraint import (
    PointwiseBoundaryConstraint,
    PointwiseInteriorConstraint,
)
from modulus.continuous.validator.validator import PointwiseValidator
from modulus.continuous.inferencer.inferencer import PointwiseInferencer
from modulus.key import Key
from modulus.PDES.navier_stokes import NavierStokes
from modulus.tensorboard_utils.plotter import ValidatorPlotter, InferencerPlotter
from modulus.architecture import layers
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

对于 LDC 流，需要求解 2d 中的稳态不可压缩 Navier-stokes 方程。因此问题的自变量是 x和y， 要解决的变量是u、v 和p。 为了表示这个问题的解决方案，创建一个神经网络在给定方程和边界条件下来给出这些变量的近似解。该网络将x、y作为输入，u、v、p作为输出。这个问题需要的偏微分方程是x和y方向的连续性和动量方程， 如下图所示：

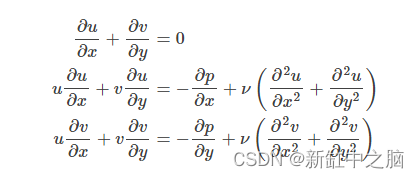
在 Modulus 中，可以使用 NavierStokes PDE 并通过为 time 和 dim 指定适当的参数来 定义这些方程。由于这是一个二维问题稳态问题，设置 time=False 和 dim=2 。同时还将问题的运动粘度（kinematic）和密度（density）分别定义0.01和0.1。

instantiate_arch() 函数的 cfg.arch参数可用于为问题创建神经网络。默认的 FullyConnectedArch 代表一个 6 层 MLP（多层感知器）架构，每层包含 512 个节点并使用 swish 激活函数。所有这些参数都是用户可配置的，但对于这个问题，默认值应该可以工作。一旦定义了所有的偏微分方程和架构，创建一个节点列表，以传如你希望该问题满足的不同约束（即方程残差、边界条件等）。

下面就是创建神经网络节点的代码：

   # make list of nodes to unroll graph on
    ns = NavierStokes(nu=0.01, rho=1.0, dim=2, time=False)
    flow_net = instantiate_arch(
        input_keys=[Key("x"), Key("y")],
        output_keys=[Key("u"), Key("v"), Key("p")],
        cfg=cfg.arch.fully_connected,
    )
    nodes = ns.make_nodes() + [flow_net.make_node(name="flow_network", jit=cfg.jit)]
1
2
3
4
5
6
7
8

使用 Modulus 的核心是 Hydra 配置文件，本示例的配置文件位于下面显示的代码中。使用 hydra 可以使用高度可定制但用户友好的方法来配置 Modulus 的大部分功能。更多信息可以在Modulus Configuration中找到。

defaults :
  - modulus_default
  - arch:
      - fully_connected
  - scheduler: tf_exponential_lr
  - optimizer: adam
  - loss: sum
  - _self_
jit: false
scheduler:
  decay_rate: 0.95
  decay_steps: 4000

training:
  rec_validation_freq: 1000
  rec_inference_freq: 2000
  rec_monitor_freq: 1000
  rec_constraint_freq: 2000
  max_steps : 10000

batch_size:
  TopWall: 1000
  NoSlip: 1000
  Interior: 4000
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

3、创建LDC几何

现在已经定义了 PDE 和架构，可以使用 Modulus 中的 CSG 模块生成 LDC 几何。CSG 模块支持多种基元，如 2D 中的矩形、圆形、三角形、无限通道、线和 3D 中的球体、圆锥体、长方体、无限通道、平面、圆柱体、圆环、四面体和三棱柱。其他复杂的几何图形可以使用这些图元通过执行加、减、相交等操作来构建。请参阅源代码文档以获取有关每个形状的定义模式以及新添加几何图形的更新的更多详细信息。

首先定义几何所需的符号变量，然后使用Rectangle几何对象生成 2D 方形几何。符号变量将用于稍后对几何进行子采样以创建不同的边界、内部区域等，同时定义约束。

在 Modulus 中，Rectangle使用两个相对角点的坐标来定义 a。下面的代码显示了在 Modulus 中生成简单几何图形的过程：

   # make geometry
    height = 0.1
    width = 0.1
    x, y = Symbol("x"), Symbol("y")
    rec = Rectangle((-width / 2, -height / 2), (width / 2, height / 2))
1
2
3
4
5

要可视化几何，可以在边界或几何内部进行采样。下面显示了一种这样的方法，其中 sample_boundary 方法对几何边界上的点进行采样。 sample_boundary 可以替换为 sample_interior 以便在几何内部采样。

var_to_polyvtk 函数将为几何图形生成一个 .vtp 点云文件，可以使用 ParaView 或任何其他点云绘图软件等工具进行查看。

samples = geo.sample_boundary(1000)
var_to_polyvtk(samples, './geo')
1
2

几何模块还提供类似 translate和rotate生成任意方向形状的功能。这些方法的使用将在后续教程中介绍。

4、添加约束条件

在开始定义问题的约束之前，让我们设置问题域。

使用Solver类 时，Domain和配置将作为输入传入。除了约束之外，你还可以向Domain中添加各种其他实用程序，例如监视器、验证数据、要对其进行推理的点等。本示例及后续示例中将详细介绍这些内容：

    # make ldc domain
    ldc_domain = Domain()
1
2

现在让我们看看如何向这个域添加约束。这可以被认为是为神经网络优化添加特定的约束。对于这个物理驱动的问题，这些约束是边界条件和方程残差。目标是完全满足边界条件，理想情况下 PDE 残差为 0。这些约束可以在 Modulus 中使用 PointwiseBoundaryConstrant和 PointwiseInteriorConstraint等类来指定。然后从这些约束构造一个 L2 损失（默认并且可以修改），优化器使用这些约束来进行最小化。以这种方式指定约束称为软约束。以下是如何指定这些约束。

4.1 边界约束

为了在 Modulus 中生成边界条件，对几何体所需边界/表面上的点进行采样，指定要在这些点上展开（评估）的节点，然后为它们分配你想要的真实值。

可以使用PointwiseBoundaryConstraint 对边界进行采样，这将对你在geometry参数中指定的几何图形的整个边界进行采样。在这种情况下，一旦你设置了 geometry=rec，矩形的所有边都被采样。通过criteria参数，可以使用特定标准对几何的特定边界进行二次采样。条件可以是使用 sympy库定义的任何符号函数。例如，要对顶壁进行采样，可以将标准设置为criteria=Eq(y,height/2)。

边界条件的所需值在outvar参数中列为字典。

使用batch_size参数指定每个边界上要采样的点数 。

注意：

• criteria参数是可选的。如果没有criteria，几何体中的所有边界都会被采样。
• 网络目录将仅显示单批采样的点。然而，训练中使用的总点数可以通过将批大小进一步乘以 batch_per_epoch 参数来计算。其默认值设置为 1000。在上面的示例中，在 Top BC 上采样的总点数将为 1000 X 1000 = 1000000。

对于 LDC 问题，将顶壁的速度u定义为+ve x方向速度为 1 m/s，而所有其他壁都是静止的（u,v = 0）。从下图 可以看出，这会产生明显的不连续性，其中速度u从0抖变至1.0。如理论部分的空间加权（SDF 加权）中所述，可以通过指定此边界的权重以使损失的权重在边界上为 0 来避免这种情况。可以使用函数 1.0 - 20.0|x| ，如下图所示 。与方程加权损失的优点类似，消除这种不连续性可以加快收敛速度​​并获得更好的精度：

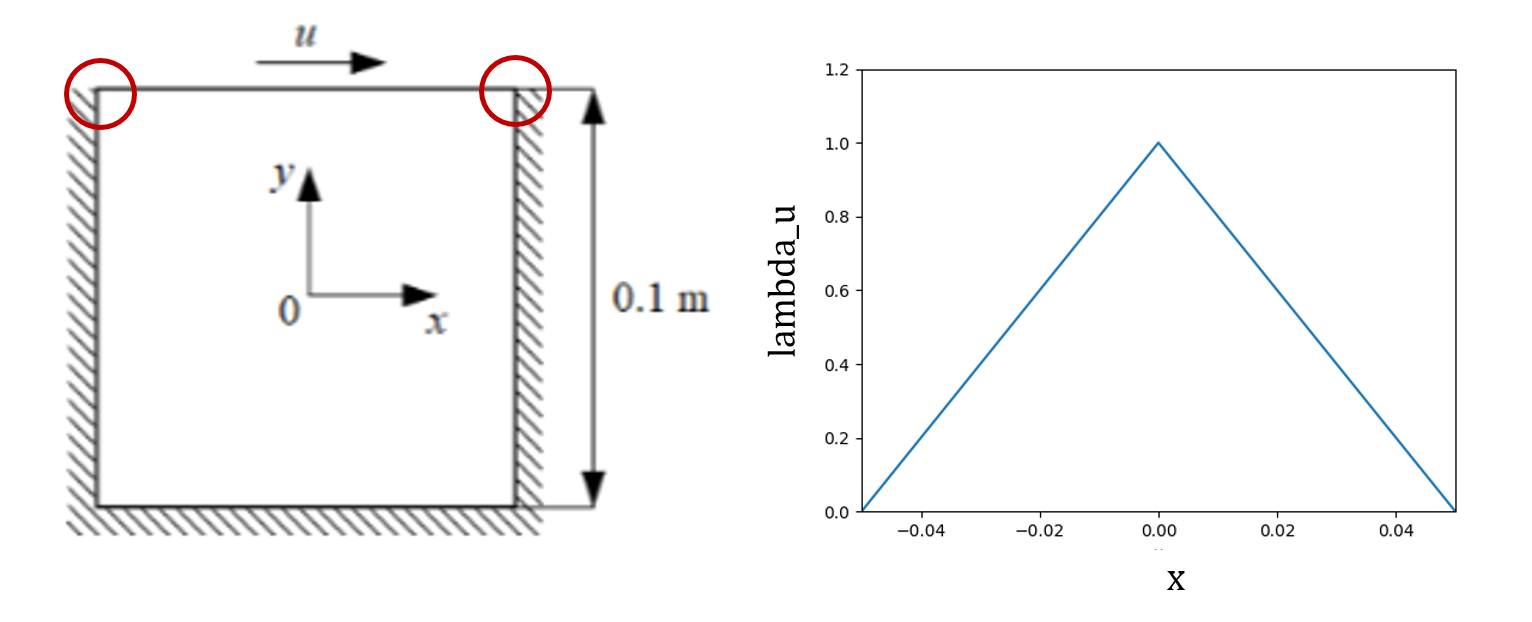
4.2 PDE约束

前面定义的问题的 PDE 需要在几何内部的所有点上强制执行，以实现所需的解决方案。为此，需要对所需几何图形内的点进行采样，指定要在这些点上展开（评估）的节点，然后为它们分配想要的真实值。

与采样边界类似，用于PointwiseInteriorConstraint对几何内部的点进行采样。要求解的方程被指定为outvar参数的字典输入。

对于 2D LDC 情况，需要 x 和 y 方向的连续性方程和动量方程。因此需要为 ‘continuity’ 、‘momentum_x’和’momentum_y’ 指定值。将值 0 分配给这些键。这表示这些键在所选点（在这种情况下是 ldc 几何结构的所有内部）的所需残差。可以为这些键指定任何值，这就像添加自定义强制/源项一样。更多示例可以在后续教程中找到，但通常，如果要添加任何源条目，可以将值 0 替换为源值。要查看方程式键是如何定义的，可以参考 Modulus 源代码 ( modulus/PDES/navier_stokes.py)。

例如，'continuity’这里给出了 的定义。

    # set equations
    self.equations = {}
    self.equations['continuity'] = rho.diff(t) + (rho*u).diff(x) + (rho*v).diff(y) + (rho*w).diff(z)
1
2
3

所产生的损失现在按以下等式表示：

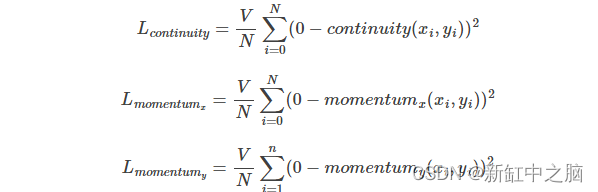
参数bounds确定对变量 x 和 y 的值进行采样的范围。lambda参数用于确定不同损失的权重。在这个问题中，我们使用几何体的有符号距离场 (SDF) 对每个点的每个方程与边界的距离进行加权。这意味着远离边界的点的权重高于靠近边界的点。这种类型的损失函数加权导致更快的收敛，因为它避免了边界处的不连续性。

lambda参数是可选的。如果未指定，则每个方程/边界变量在每个点的损失均等加权。

现在让我们看看这是如何在代码中完成的：

# top wall
    top_wall = PointwiseBoundaryConstraint(
        nodes=nodes,
        geometry=rec,
        outvar={"u": 1.0, "v": 0},
        batch_size=cfg.batch_size.TopWall,
        lambda_weighting={"u": 1.0 - 20 * Abs(x), "v": 1.0},  # weight edges to be zero
        criteria=Eq(y, height / 2),
    )
    ldc_domain.add_constraint(top_wall, "top_wall")

    # no slip
    no_slip = PointwiseBoundaryConstraint(
        nodes=nodes,
        geometry=rec,
        outvar={"u": 0, "v": 0},
        batch_size=cfg.batch_size.NoSlip,
        criteria=y < height / 2,
    )
    ldc_domain.add_constraint(no_slip, "no_slip")

    # interior
    interior = PointwiseInteriorConstraint(
        nodes=nodes,
        geometry=rec,
        outvar={"continuity": 0, "momentum_x": 0, "momentum_y": 0},
        batch_size=cfg.batch_size.Interior,
        bounds={x: (-width / 2, width / 2), y: (-height / 2, height / 2)},
        lambda_weighting={
            "continuity": rec.sdf,
            "momentum_x": rec.sdf,
            "momentum_y": rec.sdf,
        },
    )
    ldc_domain.add_constraint(interior, "interior")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

4.3 添加验证节点

你可以添加 CFD 数据或来自任何其他 PDE 求解器的数据，并使用它与 Modulus 的结果进行比较。本节介绍如何在 Modulus 中设置这样的验证域。这里使用开源 CFD 求解器 OpenFOAM 的结果进行比较。结果可以作为.csv文件（或任何其他数据格式，如 .npz , vtk 等）导入 Modulus 。需要将数据转换为用于输入和输出的 numpy 变量字典，以便在 Modulus 中使用它们。对于 csv 文件，这可以使用 csv_to_dict函数来完成。

然后使用PointwiseValidator将验证数据添加到域中。为输入和输出变量生成的 numpy 数组字典用作输入：

    # add validator
    mapping = {"Points:0": "x", "Points:1": "y", "U:0": "u", "U:1": "v", "p": "p"}
    openfoam_var = csv_to_dict(
        to_absolute_path("openfoam/cavity_uniformVel0.csv"), mapping
    )
    openfoam_var["x"] += -width / 2  # center OpenFoam data
    openfoam_var["y"] += -height / 2  # center OpenFoam data
    openfoam_invar_numpy = {
        key: value for key, value in openfoam_var.items() if key in ["x", "y"]
    }
    openfoam_outvar_numpy = {
        key: value for key, value in openfoam_var.items() if key in ["u", "v"]
    }
    openfoam_validator = PointwiseValidator(
        openfoam_invar_numpy,
        openfoam_outvar_numpy,
        nodes,
        batch_size=1024,
        plotter=ValidatorPlotter(),
    )
    ldc_domain.add_validator(openfoam_validator)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

5、训练

使用刚刚创建的域以及定义优化器选择的其他配置创建一个求解器，使用 Modulus 的Solver类设置（即conf）。然后可以使用 solve方法执行求解器：

    # make solver
    slv = Solver(cfg, ldc_domain)

    # start solver
    slv.solve()


if __name__ == "__main__":
    run()
1
2
3
4
5
6
7
8
9

为 Modulus 设置的文件现已完成。现在已准备好使用 Modulus 的神经网络求解器来求解 CFD 模拟。

6、训练模型

现在可以通过执行 python 脚本简单地开始训练：

python ldc_2d.py
1

控制台应该在每一步打印损失。但是，很难通过命令窗口监控收敛，可以改用 Tensorboard，以图形方式监控训练过程中的损失。

8、结果和后处理

Tensorboard是机器学习实验可视化的绝佳工具。为了可视化各种训练和验证损失，张量板可以设置如下：

1、在单独的终端窗口中，导航到示例的工作目录examples/ldc/
2、在命令行中输入以下命令：
···
tensorboard --logdir=./ --port=7007
···

指定要使用的端口。此示例使用 7007. 运行后，命令提示符会显示结果的 url。

3、要查看结果，请打开 Web 浏览器并转到命令提示符中提到的 url。例如： http://localhost:7007/#scalars ，将在浏览器窗口中打开一个窗口。

Tensorboard 窗口显示训练期间每个步骤的各种损失。AdamOptimizer 损失是网络计算的总损失。 “loss_L2continuity”、 “loss_L2momentum_x” 和 “loss_L2momentum_y” 分别确定在 x 和 y 方向上为连续性和 Navier Stokes 方程计算的 L2 损失。“loss_L2u”和“loss_L2v”确定边界条件的满足程度（软约束）。

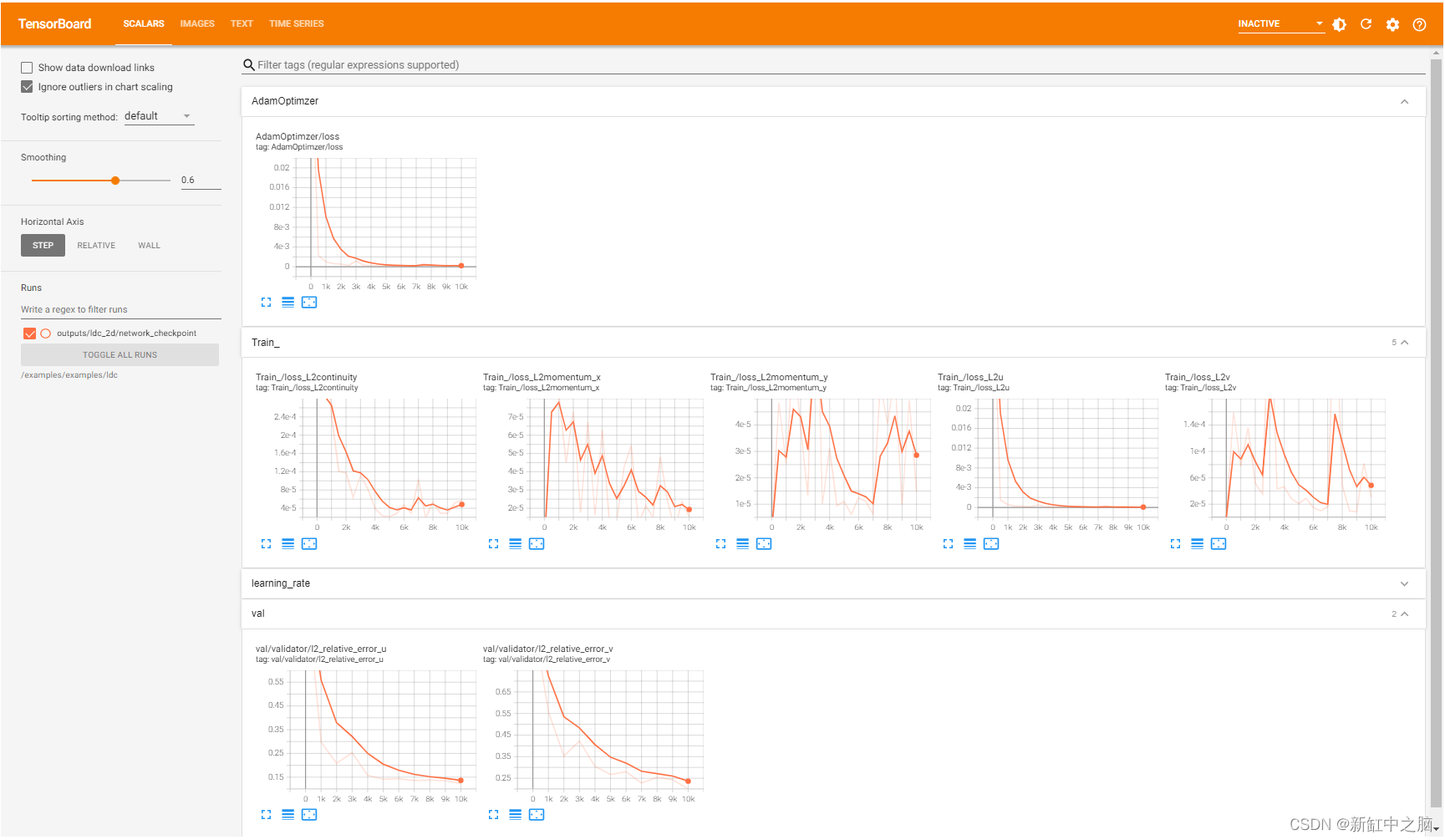
8.1 输出文件

根据’rec_results_freq’ 中指定的频率保存检查点目录。 网络目录文件夹’outputs/'包含以下重要文件/目录。

• optim_checkpoint.pth, flow_network.pth: 优化器检查点和训练期间保存的流网络。
• constraints：此目录包含使用add_constraint()添加到域中的点计算的数据。数据以 .vtp 文件的形式存在。可以使用 Paraview 等可视化工具查看 .vtp 文件。你将看到传递给 nodes约束参数的所有节点的真实值和预测值。例如， ./constraints/Interior.vtp将具有代表网络预测的变量pred_continuity和true_continuity 为 设置的真实值continuity。下图显示了真实连续性和计算连续性之间的比较。该目录有助于查看边界条件和方程在采样点处的满足程度：
  

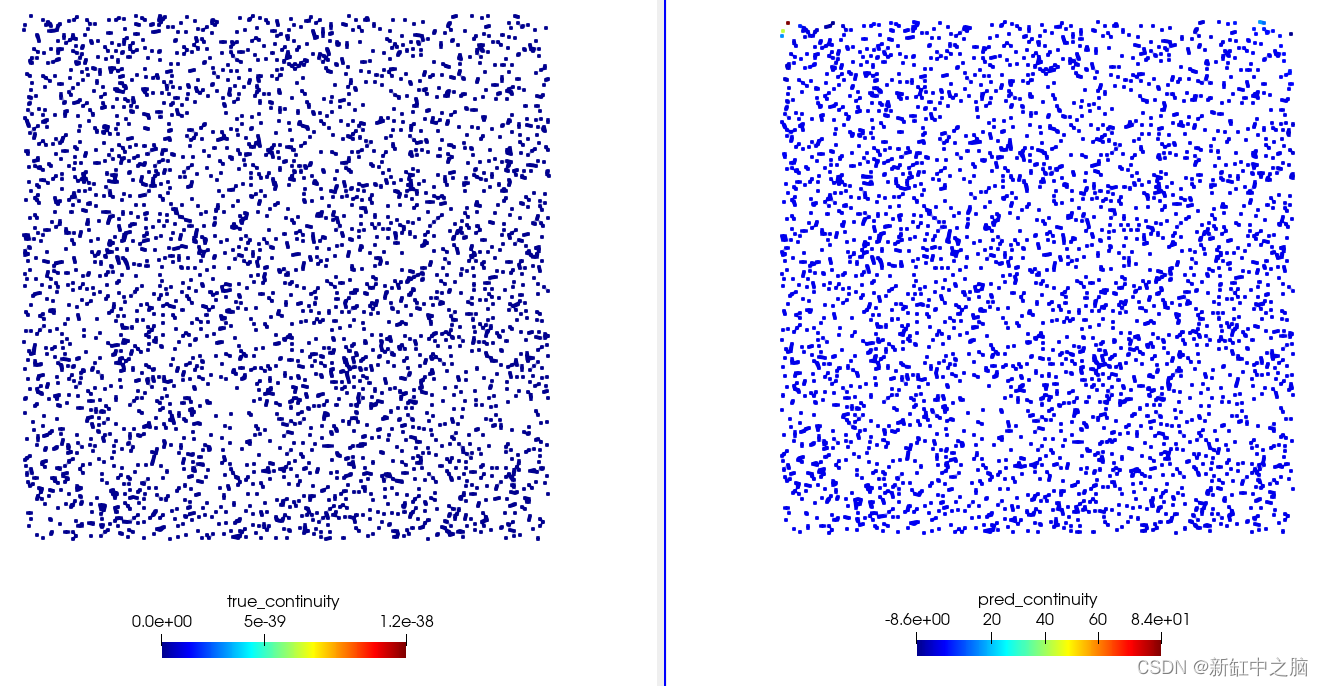
使用 Paraview 进行可视化。左：域定义中指定的连续性。右图：训练后的计算连续性

• validators:此目录包含使用add_validator()在域中添加的点计算的数据。此域对于验证参考解决方案的数据更有用。数据采用 .vtp 和 .npz 文件的形式（基于save_filetypesin 配置）。可以使用 Paraview 等可视化工具查看 .vtp 文件。此目录中的 .vtp/.npz 文件将报告所选点的预测、真实（验证数据）、预测（模型推断）。例如，./validators/validator.vtp 包含true_u、true_v、true_p和pred_u、等变量pred_v，pred_p 它们对应于“u”、“v”和“p”等变量的真实值和网络预测值。下图显示了这些变量的真实值和模量预测值之间的比较：

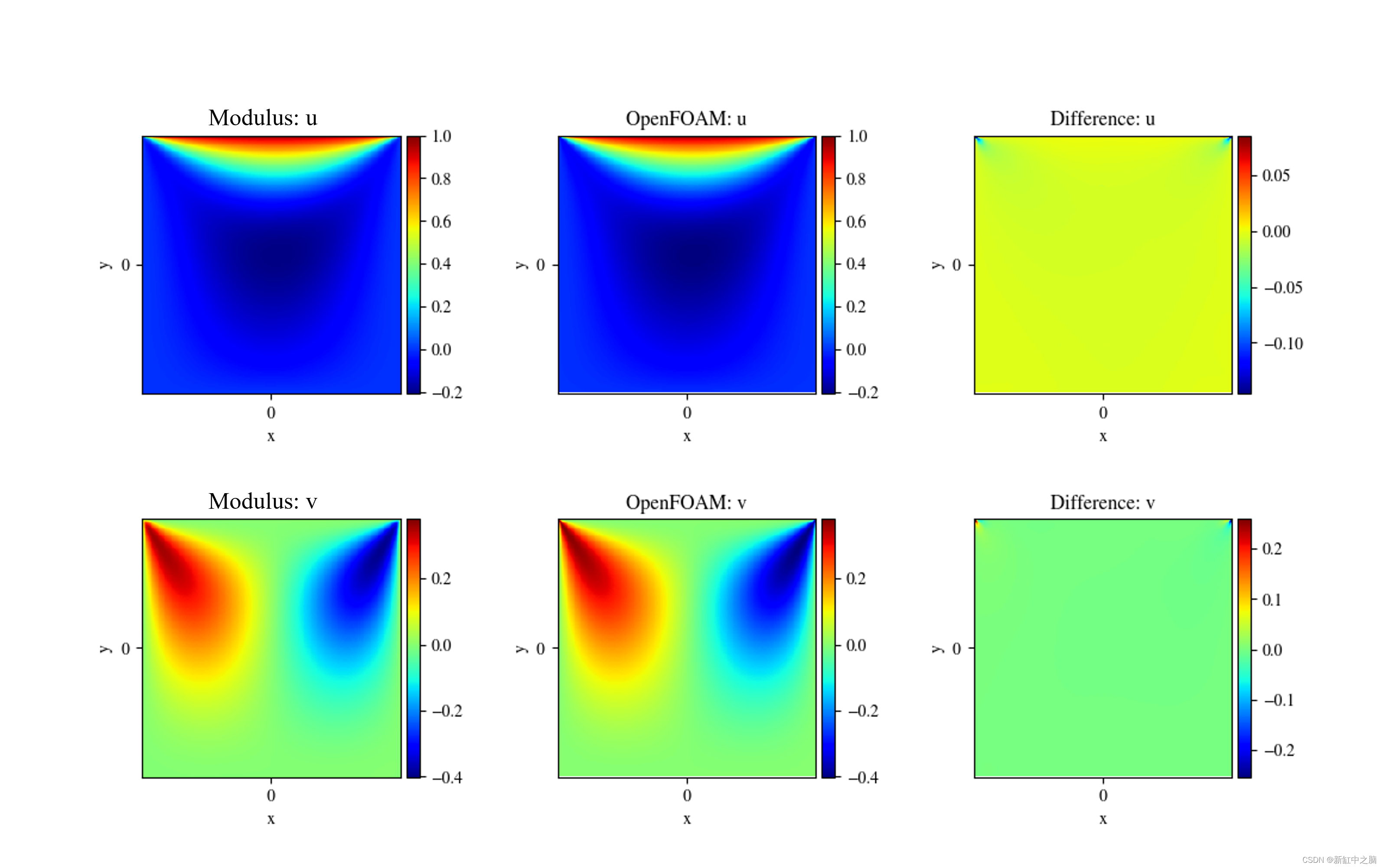
与 OpenFOAM 结果的比较

8.2 监控节点

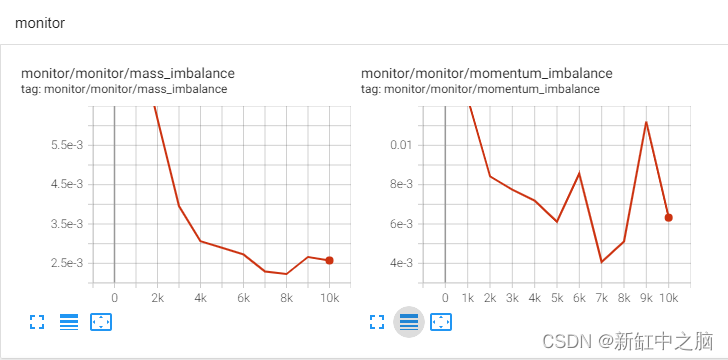
Modulus 允许你通过随着模拟的进行在 Tensorboard 中每隔固定次数的迭代绘制所需的量来监控所需的量，并根据监控量的相对变化分析收敛性。PointwiseMonitor可用于创建这样的特征。此类量的示例可以是变量的点值、表面平均值、体积平均值或可以使用正在求解的变量形成的任何导出量。

流变量可用作 PyTorch 张量。可以执行张量操作来创建你选择的任何所需的派生变量。在下面的代码中，我们创建了内部连续性和动量不平衡的监视器。

可以以与我们指定一些内部约束类似的方式选择要采样的点。

...
     # add monitors
     global_monitor = PointwiseMonitor(
         rec.sample_interior(4000, bounds={x: (-width/2, width/2), y: (-height/2, height/2)}),
         output_names=["continuity", "momentum_x", "momentum_y"],
         metrics={
             "mass_imbalance": lambda var: torch.sum(
                 var["area"] * torch.abs(var["continuity"])
             ),
             "momentum_imbalance": lambda var: torch.sum(
                 var["area"]
                 * (torch.abs(var["momentum_x"]) + torch.abs(var["momentum_y"]))
             ),
         },
         nodes=nodes,
     )
     ldc_domain.add_monitor(global_monitor)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

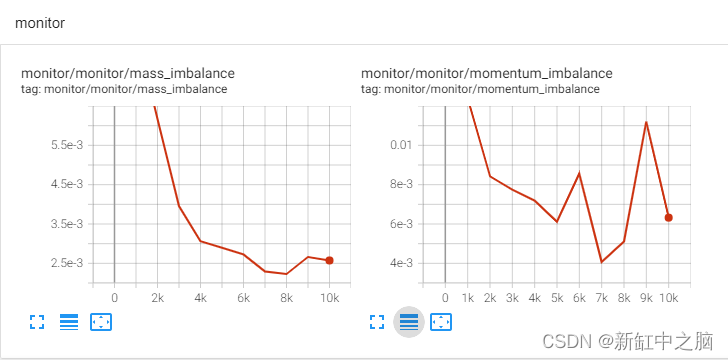
Tensorboard 中的 LDC 监视器

8.3 推理节点

Modulus 还允许你在任意域上绘制结果。然后，你可以在 ParaView 或 Tensorboard 本身中监控这些域。有关如何将 Modulus 内容添加到 Tensorboard 的更多详细信息，请参见Modulus 中的 TensorBoard。下面的代码显示了PointwiseInferencer 的使用方法。

Tensorboard 中的 LDC 推理

---

原文链接：Nvidia Modulus仿真入门 — BimAnt