Python——LSTM、GRU 时间序列股票数据预测（文末完整代码）_python股票预测代码

GRU 是在 LSTM 基础上的简化，将 LSTM 内部的三个闸门简化成两个，往往 GRU 的计算效果会优于 LSTM

目录

1. 导入工具包

2. 获取数据集

3. 数据预处理

4. 时间序列滑窗

5. 数据集划分

6. 构造网络模型

7. 网络训练

8. 查看训练过程信息

9. 预测阶段

10. 对比 LSTM 和 GRU

11.源代码

1. 导入工具包

如果没有电脑没有GPU的话就把下面那段调用GPU加速计算的代码删了

import tensorflow as tf

from tensorflow import keras

from tensorflow.keras import layers

import matplotlib.pyplot as plt

# 调用GPU加速

gpus = tf.config.experimental.list_physical_devices(device_type='GPU')

for gpu in gpus:

        tf.config.experimental.set_memory_growth(gpu, True)

2. 获取数据集

首先，安装一下 pandas_datareader 这个能远程获取金融数据的工具包。接下来使用 web.DataReader() 指定在哪个平台获取哪个公司的股票信息。具体的函数参数请看知乎专栏：【Python搞量化】pandas_datareader 经济和金融数据读取API介绍 - 知乎

本次我们获取谷歌在2000年到2021年的股票信息，把原始数据读入进来后的一定要删除数据中的空缺值，避免对后续数据处理的影响。为了方便循环神经网络的学习，需要将数据按照从旧到新的顺序排列。

本节是通过一个序列来预测10天后的股票收盘价格。在数据表格中新添 'label' 列保存每个序列的标签值。是对一个时间点的预测。

# pip install pandas_datareader

import pandas_datareader.data as web

import datetime  # datetime是Python处理日期和时间的标准库。

# 设置获取股票的时间范围的数据

start = datetime.datetime(2000,1,1)  # 设置开始时间

end = datetime.datetime(2021,9,1)  # 设置结束时间

# 在stooq数据源上获取googl在2000-2021年的股票数据

df = web.DataReader('GOOGL', 'stooq', start, end)

# 查看股票信息, 时间, 开盘价, 最高价, 最低价, 收盘价, 交易量

print(df)

df.dropna(inplace=True)  # 删除表格中的空值

# 根据数据的索引（时间）从小到大排序

df.sort_index(inplace=True)  # 排序完成后替换原来的df

print(df)

# 获取标签，预测10天后的收盘价

pre_days = 10

# 添加一个新的列存放标签, 相当于通过2004-08-19的特征来预测2004-08-29的收盘价

df['label'] = df['Close'].shift(-pre_days)

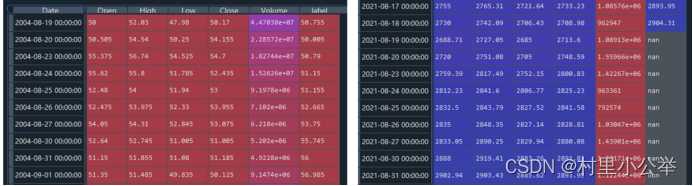
print(df)

 由于 'label' 列是将 'Close' 列集体向上移动10行，因此，'label' 列最后的10行会出现空缺值nan，这里要注意，后续会处理。

3. 数据预处理

导入 sklearn 标准化方法，对所有的特征数据进行标准化处理，对标签数据 'label' 列不做处理。标准化后能够避免偏差过大的数据对训练结果的影响。

from sklearn.preprocessing import StandardScaler  # 导入数据标准化方法

scaler = StandardScaler()  # 接收数据标准化方法

# 对所有的特征数据进行标准化，最后一列是标签值

sca_x = scaler.fit_transform(df.iloc[:,:-1])

# 查看标准化后的特征数据

print(sca_x)

五个特征列分别对应：开盘价，最高价，最低价，收盘价，交易量

4. 时间序列滑窗

这里使用一个很方便的队列deque，指定这个队列的最大长度maxlen=20，就代表一个时间序列的长度为20，如果队列deq的长度超过20就将第1个特征删除，将第21个特征追加到第20个特征后面，就能一直保持队列的长度是20。那么每一个时间序列的shape=[20,5]，代表20行数据5列特征。

完成对所有数据的时间序列分组之后，由于特征数据sca_x最后10行是没有对应的标签值的。因此需要把最后10组时间序列删除。每一个序列对应一个标签，标签和序列的长度是相同的。

import numpy as np

from collections import deque  # 相当于一个列表，可以在两头增删元素

men_his_days = 20  # 用20天的特征数据来预测

# 创建一个队列, 长度等于记忆的天数，时间序列滑窗大小=20

deq = deque(maxlen=men_his_days)

# 创建一个特征列表，保存每个时间序列的特征

x = []

# 遍历每一行特征数据

for i in sca_x:

    # 将每行特征保存进队列

    deq.append(list(i))  # array类型转为list类型

    # 如果队列的长度等于记忆的天数（时间滑窗的的长度）就证明特征组成了一个时间序列

    # 如果队列长度大于记忆天数，队列会自动将头端的那个特征删除，将新输入追加到队列尾部

    if len(deq) == men_his_days:

        # 将这一组序列保存下来

        x.append(list(deq))  # array类型转为list类型

# 由于原特征中最后10条数据没有标签值, 在x特征数据中将最后10个序列删除

x = x[:-pre_days]

# 查看有多少个序列

print(len(x))  # 4260

# 数据表格df中最后一列代表标签值, 把所有标签取出来

# 例如使用[0,1,2,3,4]天的特征预测第20天的收盘价, 使用[1,2,3,4,5]天的特征预测第21天的收盘价

# 而表格中索引4对应的标签就是该序列的标签

y = df['label'].values[men_his_days-1: -pre_days]

print(len(y))  # 序列x和标签y的长度应该一样

# 将特征和标签变成numpy类型

x, y = np.array(x), np.array(y)

5. 数据集划分

我们已经获得了处理后的时间序列和对应的标签，接下来就按比例划分训练集、验证集、测试集即可。对于训练集需要使用 .shuffle() 随机打乱数据行排列顺序，避免偶然性。设置迭代器 iter()，结合 next() 函数从训练集中取出一个batch的数据

total_num = len(x)  # 一共多少组序列和标签

train_num = int(total_num*0.8)  # 80%的数据用于训练

val_num = int(total_num*0.9)  # 80-90%的数据用于验证

# 剩余的数据用于测试

x_train, y_train = x[:train_num], y[:train_num]  # 训练集

x_val, y_val = x[train_num:val_num], y[train_num:val_num]  # 验证集

x_test, y_test = x[val_num:], y[val_num:]  # 测试集

# 转为tensor类型

batch_size = 128  # 每个step训练多少组序列数据

# 训练集

train_ds = tf.data.Dataset.from_tensor_slices((x_train, y_train))

train_ds = train_ds.batch(batch_size).shuffle(10000)  # 随机打乱

# 验证集

val_ds = tf.data.Dataset.from_tensor_slices((x_val, y_val))

val_ds = val_ds.batch(batch_size)

# 测试集

test_ds = tf.data.Dataset.from_tensor_slices((x_test, y_test))

test_ds = test_ds.batch(batch_size)

# 查看数据集信息

sample = next(iter(train_ds))  # 取出一个batch的数据

print('x_train.shape:', sample[0].shape)  # (128, 20, 5)

print('y_train.shape:', sample[1].shape)  # (128,)

6. 构造网络模型

这里以 GRU 网络为例，LSTM 只需要将下面代码中的 layers.GRU() 换成 layers.LSTM() 即可。

要注意参数 return_sequences，代表返回输出序列中的最后一个值，还是所有值。默认False。一般是下一层还是 LSTM 的时候才用 return_sequences=True

input_shape = sample[0].shape[-2:]  # [20,5] 输入维度不需要写batch维度

# 构造输入层

inputs = keras.Input(shape=input_shape)  # [None,20,5]

# 第一个GRU层, 如果下一层还是LSTM层就需要return_sequences=True, 否则就是False

x = layers.GRU(8, activation='relu', return_sequences=True, kernel_regularizer=keras.regularizers.l2(0.01))(inputs)

x = layers.Dropout(0.2)(x)  # 随机杀死神经元防止过拟合

# 第二个GRU层

x = layers.GRU(16, activation='relu', return_sequences=True, kernel_regularizer=keras.regularizers.l2(0.01))(x)

x = layers.Dropout(0.2)(x)  

# 第三个GRU层

x = layers.GRU(32, activation='relu')(x)

x = layers.Dropout(0.2)(x)  

# 全连接层, 随机权重初始化, l2正则化

x = layers.Dense(16, activation='relu', kernel_initializer='random_normal', kernel_regularizer=keras.regularizers.l2(0.01))(x)

x = layers.Dropout(0.2)(x)  

# 输出层, 输入序列的10天后的股票，是时间点。保证输出层神经元个数和y_train.shape[-1]相同

outputs = layers.Dense(1)(x)

# 构造网络

model = keras.Model(inputs, outputs)

# 查看网络结构

model.summary()

查看网络结构

Model: "model_3"

_________________________________________________________________

Layer (type)                 Output Shape              Param #   

=================================================================

input_4 (InputLayer)         [(None, 20, 5)]           0         

_________________________________________________________________

gru_3 (GRU)                  (None, 20, 8)             360       

_________________________________________________________________

dropout_12 (Dropout)         (None, 20, 8)             0         

_________________________________________________________________

gru_4 (GRU)                  (None, 20, 16)            1248      

_________________________________________________________________

dropout_13 (Dropout)         (None, 20, 16)            0         

_________________________________________________________________

gru_5 (GRU)                  (None, 32)                4800      

_________________________________________________________________

dropout_14 (Dropout)         (None, 32)                0         

_________________________________________________________________

dense_6 (Dense)              (None, 16)                528       

_________________________________________________________________

dropout_15 (Dropout)         (None, 16)                0         

_________________________________________________________________

dense_7 (Dense)              (None, 1)                 17        

=================================================================

Total params: 6,953

Trainable params: 6,953

Non-trainable params: 0

7. 网络训练

使用预测值和标签值之间的平均绝对误差mae作为损失函数，使用均方对数误差msle作为网络的监控指标。history中保存训练时的每次迭代的mae损失和msle指标

# 网络编译

model.compile(optimizer = keras.optimizers.Adam(0.001),  # adam优化器学习率0.001

              loss = tf.keras.losses.MeanAbsoluteError(),  # 标签和预测之间绝对差异的平均值

              metrics = tf.keras.losses.MeanSquaredLogarithmicError())  # 计算标签和预测之间的对数误差均方值。

epochs = 10  # 网络迭代次数

# 网络训练

history = model.fit(train_ds, epochs=epochs, validation_data=val_ds)

训练过程如下

Epoch 1/10

27/27 [==============================] - 8s 214ms/step - loss: 395.9859 - mean_squared_logarithmic_error: 32.9226 - val_loss: 1164.5131 - val_mean_squared_logarithmic_error: 46.3883

Epoch 2/10

27/27 [==============================] - 5s 198ms/step - loss: 404.5123 - mean_squared_logarithmic_error: 28.0247 - val_loss: 1153.9086 - val_mean_squared_logarithmic_error: 20.9722

----------------------------------------------------

----------------------------------------------------

Epoch 9/10

27/27 [==============================] - 5s 200ms/step - loss: 111.9984 - mean_squared_logarithmic_error: 0.1729 - val_loss: 174.2481 - val_mean_squared_logarithmic_error: 0.0213

Epoch 10/10

27/27 [==============================] - 5s 199ms/step - loss: 101.5161 - mean_squared_logarithmic_error: 0.1041 - val_loss: 54.0906 - val_mean_squared_logarithmic_error: 0.0028

8. 查看训练过程信息

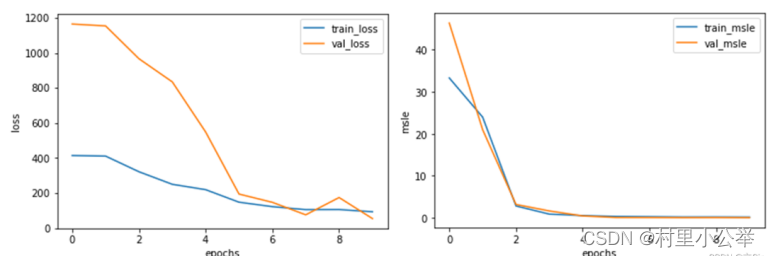
绘制每次迭代的训练集损失和验证机损失、训练集监控指标和验证集监控指标

#（10）查看训练信息

history_dict = history.history  # 获取训练的数据字典

train_loss = history_dict['loss']  # 训练集损失

val_loss = history_dict['val_loss']  # 验证集损失

train_msle = history_dict['mean_squared_logarithmic_error']  # 训练集的百分比误差

val_msle = history_dict['val_mean_squared_logarithmic_error']  # 验证集的百分比误差

#（11）绘制训练损失和验证损失

plt.figure()

plt.plot(range(epochs), train_loss, label='train_loss')  # 训练集损失

plt.plot(range(epochs), val_loss, label='val_loss')  # 验证集损失

plt.legend()  # 显示标签

plt.xlabel('epochs')

plt.ylabel('loss')

plt.show()

#（12）绘制训练百分比误差和验证百分比误差

plt.figure()

plt.plot(range(epochs), train_msle, label='train_msle')  # 训练集损失

plt.plot(range(epochs), val_msle, label='val_msle')  # 验证集损失

plt.legend()  # 显示标签

plt.xlabel('epochs')

plt.ylabel('msle')

plt.show()

9. 预测阶段

使用 evaluate() 函数对整个测试集计算损失和监控指标，获取每个真实值的时间刻度

#（13）测试集评价, 计算损失和监控指标

model.evaluate(test_ds)

# 预测

y_pred = model.predict(x_test)

# 获取标签值对应的时间

df_time = df.index[-len(y_test):]

# 绘制对比曲线

fig = plt.figure(figsize=(10,5))  # 画板大小

axes = fig.add_subplot(111)  # 画板上添加一张图

# 真实值, date_test是对应的时间

axes.plot(df_time, y_test, 'b-', label='actual')

# 预测值，红色散点

axes.plot(df_time, y_pred, 'r--', label='predict')

# 设置横坐标刻度

axes.set_xticks(df_time[::50])

axes.set_xticklabels(df_time[::50], rotation=45)

plt.legend()  # 注释

plt.grid()  # 网格

plt.show()

绘制真实值和预测值之间的对比曲线

10. 对比 LSTM 和 GRU

使用相同方法训练的LSTM和GRU的预测曲线图如下，两种方法差别不大，如果有实际需要时可对比使用。

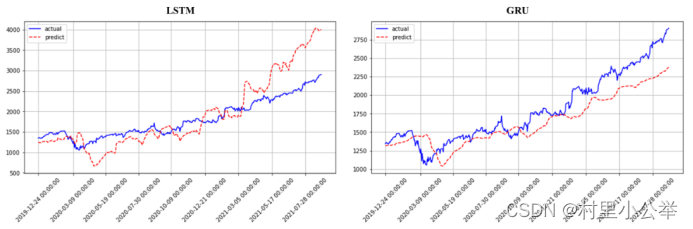
训练过程比较图

11.源代码

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
import matplotlib.pyplot as plt
 
# 调用GPU加速
gpus = tf.config.experimental.list_physical_devices(device_type='GPU')
for gpu in gpus:
    tf.config.experimental.set_memory_growth(gpu, True)
    # pip install pandas_datareader
import pandas_datareader.data as web
import datetime  # datetime是Python处理日期和时间的标准库。
 
# 设置获取股票的时间范围的数据
start = datetime.datetime(2000,1,1)  # 设置开始时间
end = datetime.datetime(2021,9,1)  # 设置结束时间
 
# 在stooq数据源上获取googl在2000-2021年的股票数据
df = web.DataReader('GOOGL', 'stooq', start, end)
# 查看股票信息, 时间, 开盘价, 最高价, 最低价, 收盘价, 交易量
print(df)
 
df.dropna(inplace=True)  # 删除表格中的空值
 
# 根据数据的索引（时间）从小到大排序
df.sort_index(inplace=True)  # 排序完成后替换原来的df
print(df)
 
# 获取标签，预测10天后的收盘价
pre_days = 10
# 添加一个新的列存放标签, 相当于通过2004-08-19的特征来预测2004-08-29的收盘价
df['label'] = df['Close'].shift(-pre_days)
print(df)
 
from sklearn.preprocessing import StandardScaler  # 导入数据标准化方法
 
scaler = StandardScaler()  # 接收数据标准化方法
# 对所有的特征数据进行标准化，最后一列是标签值
sca_x = scaler.fit_transform(df.iloc[:,:-1])
# 查看标准化后的特征数据
print(sca_x)
 
import numpy as np
from collections import deque  # 相当于一个列表，可以在两头增删元素
 
men_his_days = 20  # 用20天的特征数据来预测
# 创建一个队列, 长度等于记忆的天数，时间序列滑窗大小=20
deq = deque(maxlen=men_his_days)
 
# 创建一个特征列表，保存每个时间序列的特征
x = []
# 遍历每一行特征数据
for i in sca_x:
    # 将每行特征保存进队列
    deq.append(list(i))  # array类型转为list类型
    # 如果队列的长度等于记忆的天数（时间滑窗的的长度）就证明特征组成了一个时间序列
    # 如果队列长度大于记忆天数，队列会自动将头端的那个特征删除，将新输入追加到队列尾部
    if len(deq) == men_his_days:
        # 将这一组序列保存下来
        x.append(list(deq))  # array类型转为list类型
 
# 由于原特征中最后10条数据没有标签值, 在x特征数据中将最后10个序列删除
x = x[:-pre_days]
# 查看有多少个序列
print(len(x))  # 4260
 
# 数据表格df中最后一列代表标签值, 把所有标签取出来
# 例如使用[0,1,2,3,4]天的特征预测第20天的收盘价, 使用[1,2,3,4,5]天的特征预测第21天的收盘价
# 而表格中索引4对应的标签就是该序列的标签
y = df['label'].values[men_his_days-1: -pre_days]
print(len(y))  # 序列x和标签y的长度应该一样
 
# 将特征和标签变成numpy类型
x, y = np.array(x), np.array(y)
 
total_num = len(x)  # 一共多少组序列和标签
train_num = int(total_num*0.8)  # 80%的数据用于训练
val_num = int(total_num*0.9)  # 80-90%的数据用于验证
# 剩余的数据用于测试
 
x_train, y_train = x[:train_num], y[:train_num]  # 训练集
x_val, y_val = x[train_num:val_num], y[train_num:val_num]  # 验证集
x_test, y_test = x[val_num:], y[val_num:]  # 测试集
 
# 转为tensor类型
batch_size = 128  # 每个step训练多少组序列数据
# 训练集
train_ds = tf.data.Dataset.from_tensor_slices((x_train, y_train))
train_ds = train_ds.batch(batch_size).shuffle(10000)  # 随机打乱
# 验证集
val_ds = tf.data.Dataset.from_tensor_slices((x_val, y_val))
val_ds = val_ds.batch(batch_size)
# 测试集
test_ds = tf.data.Dataset.from_tensor_slices((x_test, y_test))
test_ds = test_ds.batch(batch_size)
 
# 查看数据集信息
sample = next(iter(train_ds))  # 取出一个batch的数据
print('x_train.shape:', sample[0].shape)  # (128, 20, 5)
print('y_train.shape:', sample[1].shape)  # (128,)
 
input_shape = sample[0].shape[-2:]  # [20,5] 输入维度不需要写batch维度
 
# 构造输入层
inputs = keras.Input(shape=input_shape)  # [None,20,5]
 
# 第一个GRU层, 如果下一层还是LSTM层就需要return_sequences=True, 否则就是False
x = layers.GRU(8, activation='relu', return_sequences=True, kernel_regularizer=keras.regularizers.l2(0.01))(inputs)
x = layers.Dropout(0.2)(x)  # 随机杀死神经元防止过拟合
 
# 第二个GRU层
x = layers.GRU(16, activation='relu', return_sequences=True, kernel_regularizer=keras.regularizers.l2(0.01))(x)
x = layers.Dropout(0.2)(x)  
 
# 第三个GRU层
x = layers.GRU(32, activation='relu')(x)
x = layers.Dropout(0.2)(x)  
 
# 全连接层, 随机权重初始化, l2正则化
x = layers.Dense(16, activation='relu', kernel_initializer='random_normal', kernel_regularizer=keras.regularizers.l2(0.01))(x)
x = layers.Dropout(0.2)(x)  
 
# 输出层, 输入序列的10天后的股票，是时间点。保证输出层神经元个数和y_train.shape[-1]相同
outputs = layers.Dense(1)(x)
 
# 构造网络
model = keras.Model(inputs, outputs)
 
# 查看网络结构
model.summary()
 
# 网络编译
model.compile(optimizer = keras.optimizers.Adam(0.001),  # adam优化器学习率0.001
              loss = tf.keras.losses.MeanAbsoluteError(),  # 标签和预测之间绝对差异的平均值
              metrics = tf.keras.losses.MeanSquaredLogarithmicError())  # 计算标签和预测之间的对数误差均方值。
 
epochs = 10  # 网络迭代次数
 
# 网络训练
history = model.fit(train_ds, epochs=epochs, validation_data=val_ds)
 
#（10）查看训练信息
history_dict = history.history  # 获取训练的数据字典
train_loss = history_dict['loss']  # 训练集损失
val_loss = history_dict['val_loss']  # 验证集损失
train_msle = history_dict['mean_squared_logarithmic_error']  # 训练集的百分比误差
val_msle = history_dict['val_mean_squared_logarithmic_error']  # 验证集的百分比误差
 
#（11）绘制训练损失和验证损失
plt.figure()
plt.plot(range(epochs), train_loss, label='train_loss')  # 训练集损失
plt.plot(range(epochs), val_loss, label='val_loss')  # 验证集损失
plt.legend()  # 显示标签
plt.xlabel('epochs')
plt.ylabel('loss')
plt.show()
 
#（12）绘制训练百分比误差和验证百分比误差
plt.figure()
plt.plot(range(epochs), train_msle, label='train_msle')  # 训练集损失
plt.plot(range(epochs), val_msle, label='val_msle')  # 验证集损失
plt.legend()  # 显示标签
plt.xlabel('epochs')
plt.ylabel('msle')
plt.show()
 
#（13）测试集评价, 计算损失和监控指标
model.evaluate(test_ds)
 
# 预测
y_pred = model.predict(x_test)
 
# 获取标签值对应的时间
df_time = df.index[-len(y_test):]
 
# 绘制对比曲线
fig = plt.figure(figsize=(10,5))  # 画板大小
axes = fig.add_subplot(111)  # 画板上添加一张图
# 真实值, date_test是对应的时间
axes.plot(df_time, y_test, 'b-', label='actual')
# 预测值，红色散点
axes.plot(df_time, y_pred, 'r--', label='predict')
# 设置横坐标刻度
axes.set_xticks(df_time[::50])
axes.set_xticklabels(df_time[::50], rotation=45)
 
plt.legend()  # 注释
plt.grid()  # 网格
plt.show()