类神经网络训练——Loss降不下来_gpt-2训练loss降不下去

Loss函数降不下来

原因与原理

在Loss没有卡住之前，我们是根据gradient（梯度）下降的方向寻找更优的函数，是的loss更小，但是，因为此时gradient为零，怎样对他求导的结果都是零，随意这时候已经找不到梯度下降的方向了。而gradient为0的情况分两种，不一定都是进入了局部最优点，还有可能是进入了鞍点，所以要判断到底是进入了那一个情况，才可以采取下一步计划，调整训练方向。

• 陷入局部最优或者陷入鞍点（所以，不一定是陷入局部最优，也有可能是陷入鞍点）

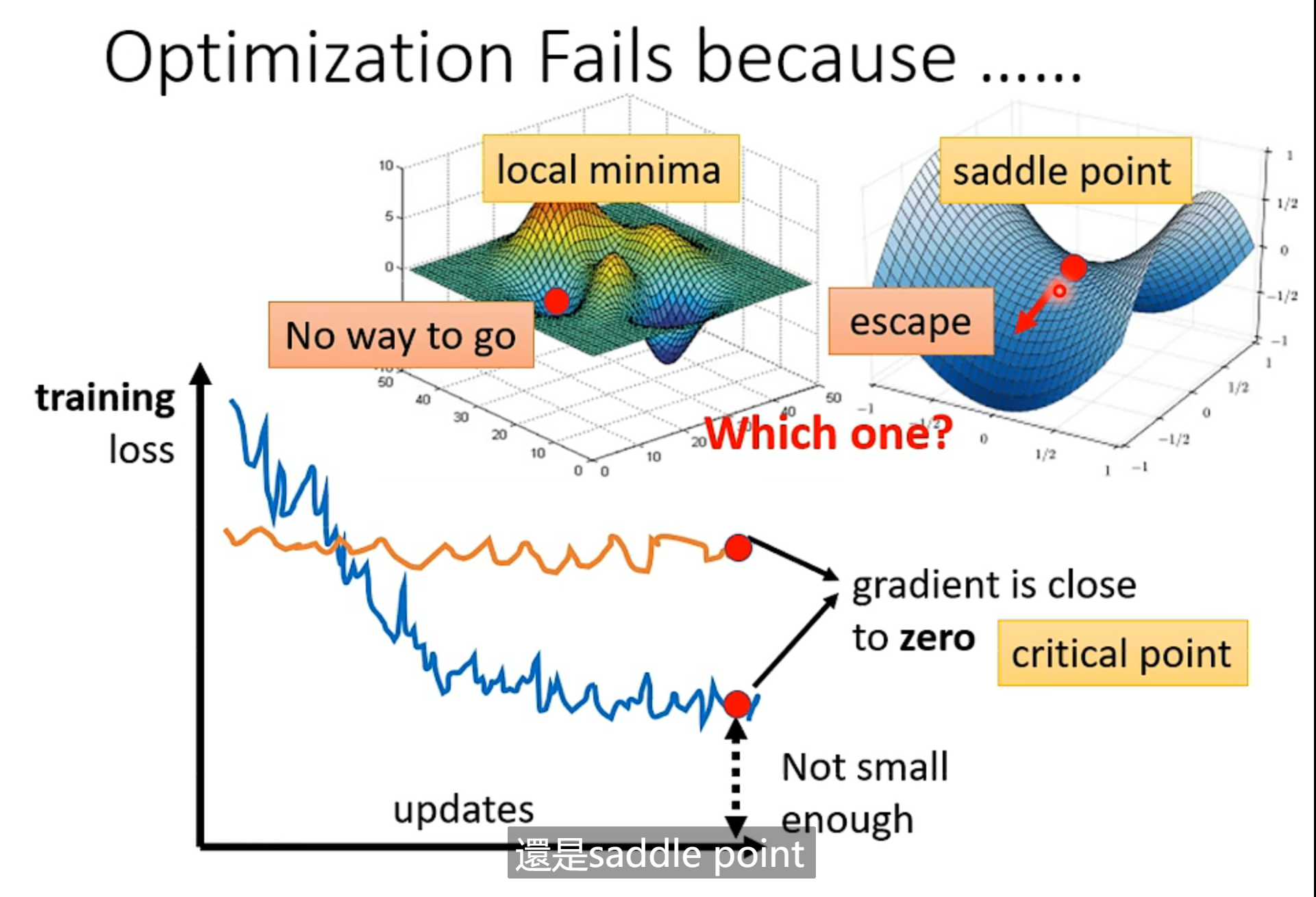
怎样判断？——海森矩阵（Hessian Matrix）

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HYiqPYm1-1656426296264)(https://s2.loli.net/2022/06/28/zn7YvVKcPNwGhyd.png)]

• 计算海森矩阵
• 计算海森矩阵的特征值
• 海森矩阵特征值全为正，陷入局部最小；海森矩阵特征值全为负，陷入局部最大；海森矩阵特征值有正有负，陷入鞍点

陷入鞍点（saddle point）的情况下

如上图所示，陷入鞍点的情况下，还是比较容易解决的。只需要找到海森矩阵的负的特征值（eigen value) $\mu$ 以及对应的特征向量（eigen vector）$H$

然后新的点$\theta$ 就等于$\theta$’+$H$（ppt中应该是写错了）

这个新的点$\theta$ 就会有更小的loss

常用解决方案

一般来说，在训练过程中遇到鞍点或者局部最值时，不会计算海森矩阵，开销太大，而是用下面的方法

momentum方法

momentum-动量

图示：滚球的时候因为有动量的存在所以球一般不会卡在鞍点或者局部最小点

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2PQPoXVj-1656426296265)(https://s2.loli.net/2022/06/28/B1vWpOkHJMKfZhw.png)]

在一般的梯度下降法中，是通过计算gradient

根据公式

$\theta^1$=$\theta^0$-n$g^0$

更新方向是梯度gradient的反方向，如图

而momentum技术是不仅考虑梯度计算指示 的方向，还要同时考虑前一步的移动方向

下一步的移动方向=上一步的移动方向+梯度指示的方向

如图：

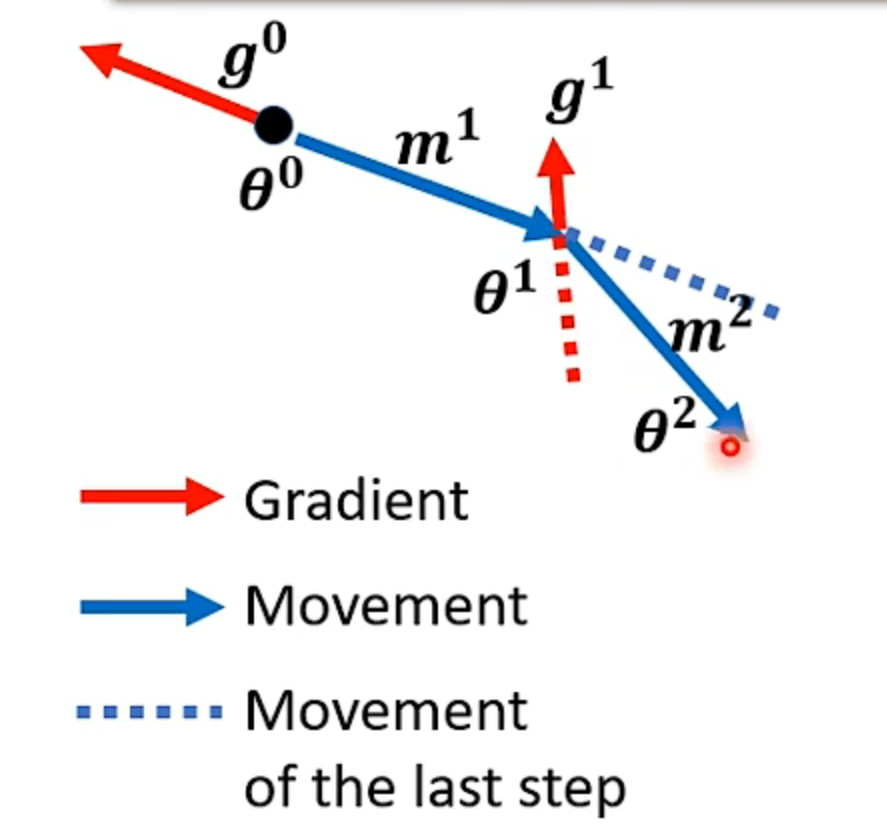
而且在计算移动方向的公式中可以将移动方向化简消去，因为上一步的移动方向实际上是根据上一步的上一步移动方向与上一步的梯度计算出来的，在最开始的时候的移动方向是0，所以可以地推计算每一步的移动方向，从而可以只根据梯度计算移动方向

如图：

我们可以发现在加入了momentum技术之后下一步的移动方向$m^i$像是前几步梯度的加权平均一样，不仅仅只考虑本步计算出的梯度，还将前几步计算出的所有梯度都考虑进去。

#######

图源李宏毅2021ML教程

侵必删

#######