视觉slam学习|基础篇01_slam入门

系列文章目录

SLAM基础篇01
SLAM基础篇02

前言

最近在看高翔和张涛写的《视觉SLAM十四讲》，记录一下学习的内容，方便以后复习。这一系列文章更像是这本书的读书笔记，所以结构脉络都与该书相似；更推荐有时间的同学去看原书，写的更加详细易懂。欢迎大家一起探讨学习视觉SLAM相关的知识。

SLAM是干什么的？

SLAM(simultaneous localization and mapping)全称即时定位与地图构建或并发建图与定位),顾名思义可以解决“定位”和“建图“两件事情。 SLAM 问题的本质：对运动主体自身和周围环境空间不确定性的估计。主流的slam技术应用有两种，分别是激光slam(基于激光雷达lidar 来建图导航)和视觉slam(vslam,基于单/双目摄像头视觉建图导航)。

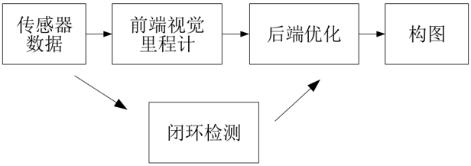
经典的视觉 SLAM 框架是过去十几年内，研究者们总结的成果。这个框架本身，以及它所包含的算法已经基本定型，并且在许多视觉程序库和机器人程序库中已经提供。依靠这些算法，我们能够构建一个视觉 SLAM 系统，使之在正常的工作环境里实时进行定位与建图。如上图所示，我们八视觉slam分为几步：

1. 传感器信息读取。在视觉 SLAM 中主要为相机图像信息的读取和预处理。如果在机器人中，还可能有码盘、惯性传感器等信息的读取和同步。
2. 视觉里程计 (Visual Odometry, VO)。视觉里程计任务是估算相邻图像间相机的运动，以及局部地图的样子。VO 又称为前端（Front End）。过视觉里程计来估计轨迹，将不可避免地出现累计漂移（Accumulating Drift）。这是由于视觉里程计（在最简单的情况下）只估计两个图像间运动造成的。我们知道，每次估计都带有一定的误差，而由于里程计的工作方式，先前时刻的误差将会传递到下一时刻，导致经过一段时间之后，估计的轨迹将不再准确。为了解决漂移问题，我们还需要两种技术：后端优化和回环检测。回环检测负责把“机器人回到原始位置”的事情检测出来，而后端优化则根据该信息，校正整个轨迹的形状。
3. 后端优化（Optimization）。后端接受不同时刻视觉里程计测量的相机位姿，以及回环检测的信息，对它们进行优化，得到全局一致的轨迹和地图。由于接在 VO 之后，又称为后端（Back End）。。后端优化要考虑的问题，
   就是如何从这些带有噪声的数据中，估计整个系统的状态，以及这个状态估计的不确定性有多大——这称为最大后验概率估计（Maximum-a-Posteriori，MAP）。
4. 回环检测（Loop Closing）。回环检测判断机器人是否曾经到达过先前的位置。如果检测到回环，它会把信息提供给后端进行处理。通
5. 建图（Mapping）。它根据估计的轨迹，建立与任务要求对应的地图。地图的形式随SLAM的应用场合而定。大体上讲，它们可以分为度量地图与拓扑地图两种。度量地图强调精确地表示地图中物体的位置关系，通常我们用稀疏（Sparse）与稠密（Dense）对它们进行分类。相比于度量地图的精确性，拓扑地图则更强调地图元素之间的关系。拓扑地图是一个图（Graph），由节点和边组成，只考虑节点间的连通性，例如A，B点是连通的，而不考虑如何从A点到达B点的过程。

SLAM的数学建模

由于相机通常是在某些时刻采集数据的，所以我们也只关心这些时刻的位置和地图。这就把一段连续时间的运动变成了离散时刻 t = 1, . . . , K 当中发生的事情。在这些时刻，用 $\mathbf{x}$ 表示小萝卜自身的位置。于是各时刻的位置就记为 x1, . . . , xK，它们构成了机器人的轨迹。地图方面，我们设地图是由许多个路标（Landmark）组成的，而每个时刻，传感器会测量到一部分路标点，得到它们的观测数据。不妨设路标点一共有 N 个，用 y1, . . . , yN表示它们。
机器人的运动方程可用下式表示：
$${\mathbf{x}}_k=f\left({\mathbf{x}}_{k-1},{\mathbf{u}}_k,{\mathbf{w}}_k\right)$$
其中，$u_k$是运动传感器的读数，$w_k$为噪声。
机器人的观测方程可用下式表示：
$${\mathbf{z}}_{k,j}=h\left({\mathbf{y}}_j,{\mathbf{x}}_k,{\mathbf{v}}_{k,j}\right)$$
这里，$v_{k,j}$是这次观测的噪声。

这两个方程描述了最基本的 SLAM 问题：当我们知道运动测量的读数 u，以及传感器的读数 z 时，如何求解定位问题（估计 x）和建图问题（估计 y）？这时，我们把 SLAM问题建模成了一个状态估计问题：如何通过带有噪声的测量数据，估计内部的、隐藏着的状态变量？

机器人学基础

齐次矩阵

在机器人学中，我们习惯用一个坐标系来表达一个刚体的位姿，机器人的位置和姿态，其实就是机器人坐标系在世界坐标系的表达。我们使用齐次矩阵T来表达两个坐标系的变换关系，很显然其次矩阵T应该包括旋转和平移两个部分。
对于刚体的旋转，我们使用旋转矩阵$\mathbf{R}$表示，她是一个行列式为1的正交矩阵。
我们可以吧旋转矩阵的的集合定义如下：
$$SO(n)=\left\{R\in {\mathbb{R}}^{n\times n}\mid R{R}^T=I,\det (R)=1\right\}.$$

$SO(n)$ 是特殊正交群 (Special Orthogonal Group) 的意思。“群” 的内容等会儿还会再说。这个集合由 $n$ 维空间的旋转矩阵组成, 特别的, $SO(3)$ 就是三维空间的旋转 了。通过旋转矩阵, 我们可以直接谈论两个坐标系之间的旋转变换, 而不用再从基开始谈 起了。换句话说, 旋转矩阵可以描述刚体的旋转。

对于刚体的平移，我们可以用一个平移向量$\mathbf{t}$来表示。那么把向量$\mathbf{a}$移动到${\mathbf{a}}^{\prime }$,可以表达为：
$$a^{\prime }=Ra+t$$

对于上面的这个式子，我们用矩阵的形式表达出来就是：
[ a ′ 1 ] = [ R t 0 T 1 ] [ a 1 ] ≜ T [ a 1 ] \left[

$$\begin{array}{l}a^{\prime} \\ 1\end{array}$$ \right]=\left[ $$\begin{array}{ll}R & t \\ 0^{T} & 1\end{array}$$ \right]\left[ $$\begin{array}{l}a \\ 1\end{array}$$ \right] \triangleq T\left[ $$\begin{array}{l}a \\ 1\end{array}$$ \right] [a′1​]=[R0T​t1​][a1​]≜T[a1​]
这里把我们向量的末尾加了一个“1”，变成了四维齐次坐标。这个T就是所谓的齐次变换矩阵，它有比较特殊的结构：左上为旋转矩阵，右侧为平移向量。左下为向量，右下为1。这种矩阵又称为特殊欧式群(Special Euclidean Group)

S E ( 3 ) = { T = [ R t 0 T 1 ] ∈ R 4 × 4 ∣ R ∈ S O ( 3 ) , t ∈ R 3 } . S E(3)=\left\{T=\left[

$$\begin{array}{cc} R & t \\ 0^{T} & 1 \end{array}$$ \right] \in \mathbb{R}^{4 \times 4} \mid R \in S O(3), t \in \mathbb{R}^{3}\right\} . SE(3)={T=[R0T​t1​]∈R4×4∣R∈SO(3),t∈R3}.
与 $SO(3)$ 一样, 求解该矩阵的逆表示一个反向的变换:
$$T^{-1}=\left[\begin{array}{cc}{R}^T& -R^{T}t\\ 0^T& 1\end{array}\right].$$

这里额外补充一点向量外积的知识：对于向量$\mathbf{a},\mathbf{b}\in {\mathbb{R}}^3$,外积可以表达为：
a × b = [ i j k a 1 a 2 a 3 b 1 b 2 b 3 ] = [ a 2 b 3 − a 3 b 2 a 3 b 1 − a 1 b 3 a 1 b 2 − a 2 b 1 ] = [ 0 − a 3 a 2 a 3 0 − a 1 − a 2 a 1 0 ] b ≜ a ∧ b . a \times b=\left[

$$\begin{array}{ccc}i & j & k \\ a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3}\end{array}$$ \right]=\left[ $$\begin{array}{c}a_{2} b_{3}-a_{3} b_{2} \\ a_{3} b_{1}-a_{1} b_{3} \\ a_{1} b_{2}-a_{2} b_{1}\end{array}$$ \right]=\left[ $$\begin{array}{ccc}0 & -a_{3} & a_{2} \\ a_{3} & 0 & -a_{1} \\ -a_{2} & a_{1} & 0\end{array}$$ \right] b \triangleq a^{\wedge} b . a×b=⎣ ⎡​ia1​b1​​ja2​b2​​ka3​b3​​⎦ ⎤​=⎣ ⎡​a2​b3​−a3​b2​a3​b1​−a1​b3​a1​b2​−a2​b1​​⎦ ⎤​=⎣ ⎡​0a3​−a2​​−a3​0a1​​a2​−a1​0​⎦ ⎤​b≜a∧b.
$$\mathbf{a}\times \mathbf{b}=\Vert \mathbf{a}\Vert \Vert \mathbf{b}\Vert \sin (\theta )\mathbf{n}$$
外积的方向垂直于这两个向量, 大小为 $|a||b|\sin ⟨a,b⟩$, 是两个向量张成的四边形的 有向面积。对于外积, 我们引入了 $\wedge$ 符号, 把 $a$ 㝍成一个矩阵。事实上是一个反对称矩阵 (Skew-symmetric), 你可以将 ${}^{\wedge }$ 记成一个反对称符号。这样就把外积 $a\times b$, 写成了矩阵 与向量的乘法 $a^{\wedge }b$, 把它变成了线件运算。这个符号将在后文经常用到, 请记住它。
外积只对三维向量存在定义, 我们还能用外积表示向量的旋转。根据右手法则，从向量a转到向量b，转动轴的方向其实就是a和b外积的方向，大小由a和b的夹角决定。

关于旋转的表示：旋转向量、欧拉角、四元数

关于刚体旋转的表示，除了上面介绍的旋转矩阵，但是旋转矩阵用9个量来表示一个三自由度的旋转，显然有些冗余，其次旋转矩阵自身带有约束，必须是行列式为1的旋转矩阵，这对我们以后的估计和优化会带来非常大的麻烦。因此有必要介绍其他的表示方法。
旋转向量
之前在介绍外积的时候提到说外积可以表示向量间的旋转。其实任意的旋转都可以用一个旋转轴和一个旋转角表示。因此我们定义一个旋转向量，其方向与旋转轴一致，长度等于旋转角。这里的旋转向量其实就是下面要接杀的李代数。对于一个旋转轴为 $\mathbf{n}$, 角度为 $\theta$ 的旋转, 显然, 它对应的旋转向 量为 $\theta \mathbf{n}$ 。由旋转向量到旋转矩阵的过程由罗德里格斯公式 (Rodrigues’s Formula) 表明, 由于推导过程比较复杂, 我们不作描述, 只给出转换的结果
$$\mathbf{R}=\cos \theta \mathbf{I}+(1-\cos \theta )\mathbf{n}{\mathbf{n}}^T+\sin \theta {\mathbf{n}}^{\wedge }.$$
这里，符号 ${}^{\wedge }$ 是向量到反对称的转换符，前面介绍向量外积的时候有提到。
当然我们也可以从旋转矩阵计算旋转向量和转角：
$$\theta =\arccos \left(\frac{\mathrm{tr}(\mathbf{R})-1}{2}\right).$$
$$\mathbf{R}\mathbf{n}=\mathbf{n}$$
转轴$\mathbf{n}$是矩阵R特征值1对应的特征向量。求解此方程，再归一化就可得到旋转轴。
欧拉角
欧拉角当中比较常用的一种，便是用“偏航-俯仰-滚转”（yaw-pitch-roll）三个角度来描述一个旋转的。由于它等价于 ZY X 轴的旋转，我们就以 ZY X 为例。
假设一个刚体的前方（朝向我们的方向）为X 轴，右侧为 Y 轴，上方为 Z 轴，见下图 。那么，ZY X 转角相当于把任意旋转分解成以下三个轴上的转角：

1. 绕物体的 Z 轴旋转，得到偏航角 yaw；
2. 绕旋转之后的 Y 轴旋转，得到俯仰角 pitch；
3. 绕旋转之后的 X 轴旋转，得到滚转角 roll。
   

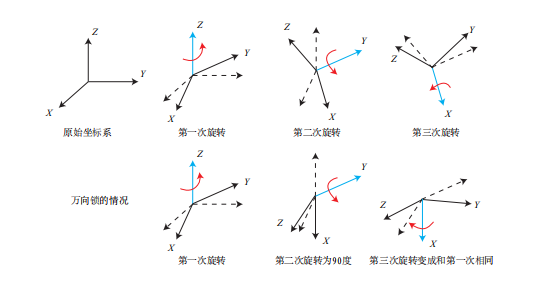
此时，我们可以使用 [r, p, y]T 这样一个三维的向量描述任意旋转。这个向量十分的直观，我们可以从这个向量想象出旋转的过程。但是欧拉角的一个重大缺点是会碰到著名的万向锁问题（Gimbal Lock①）：在俯仰角为±90◦ 时，第一次旋转与第三次旋转将使用同一个轴，使得系统丢失了一个自由度（由三次旋转变成了两次旋转）。这被称为奇异性问题，理论上可以证明，只要我们想用三个实数来表达三维旋转时，都会不可避免地碰到奇异性问题。由于这种原理，欧拉角不适于插值和迭代，往往只用于人机交互中。

四元数
事实上，我们找不到不带奇异性的三维向量描述方式 。这有点类似于，当我们想用两个坐标表示地球表面时（如经度和纬度），必定存在奇异性（纬度为 ±90◦ 时经度无意义）。三维旋转是一个三维流形，想要无奇异性地表达它，用三个量是不够的。
回忆我们以前学习过的复数。我们用复数集 $\mathbb{C}$ 表示复平面上的向量，而复数的乘法则能表示复平面上的旋转：例如，乘上复数 i 相当于逆时针把一个复向量旋转 90 度。类似的，在表达三维空间旋转时，也有一种类似于复数的代数：四元数（Quaternion）。四元数是 Hamilton 找到的一种扩展的复数. 它既是紧凑的，也没有奇异性。
一个四元数 $q$ 拥有一个实部和三个虚部, 像这样:
$$q=q_0+q_{1}i+q_{2}j+q_{3}k,$$
其中 $i,j,k$ 为四元数的三个虚部。这三个虚部满足关系式:
{ i 2 = j 2 = k 2 = − 1 i j = k , j i = − k j k = i , k j = − i k i = j , i k = − j \left\{

$$\begin{array}{l} i^{2}=j^{2}=k^{2}=-1 \\ i j=k, j i=-k \\ j k=i, k j=-i \\ k i=j, i k=-j \end{array}$$ \right. ⎩ ⎨ ⎧​i2=j2=k2=−1ij=k,ji=−kjk=i,kj=−iki=j,ik=−j​
由于它的这种特殊表示形式，有时人们也用一个标量和一个向量来表达四元数:
$$q=[s,v],s=q_0\in \mathbb{R},v={\left[q_1,q_2,q_3\right]}^T\in {\mathbb{R}}^3,$$
这里, $s$ 称为四元数的实部, 而 $v$ 称为它的虚部。如果一个四元数虚部为 0 , 称之为实四 元数。反之, 若它的实部为 0 , 称之为虚四元数。
我们可以用四元数表达对一个点的旋转。假设一个空间三维点 $\mathbf{p}=[x,y,z]\in {\mathbb{R}}^3$, 以 及一个由轴角 $\mathbf{n},\theta$ 指定的旋转。三维点 $\mathbf{p}$ 经过旋转之后变成为 ${\mathbf{p}}^{\prime }$ 。如果使用矩阵描述, 则为${\mathbf{p}}^{\prime }=\mathbf{R}\mathbf{p}$
如果用四元数来描述,首先把三维空间点用一个虚四元数来描述:
$$\mathbf{p}=[0,x,y,z]=[0,\mathbf{v}].$$
这相当于我们把四元数的三个虚部与空间中的三个轴相对应。然后,用四 元数 $\mathbf{q}$ 表示这个旋转:
$$\mathbf{q}=\left[\cos \frac{\theta }{2},\mathbf{n}\sin \frac{\theta }{2}\right].$$
反之，我们亦可从单位四元数中计算出对应旋转轴与夹角：
$$\{\begin{array}{l}\theta =2\arccos q_0\\ {\left[n_x,n_y,n_z\right]}^T={\left[q_1,q_2,q_3\right]}^T/\sin \frac{\theta }{2}\end{array}$$
对上式的 θ 加上 2π，我们得到一个相同的旋转，但此时对应的四元数变成了 −q。因此，在四元数中，任意的旋转都可以由两个互为相反数的四元数表示。同理，取 θ 为 0，则得到一个没有任何旋转的实四元数。

回到正题, 旋转后的点 ${\mathbf{p}}^{\prime }$ 即可表示为这样的乘积:
$${\mathbf{p}}^{\prime }=\mathbf{q}\mathbf{p}{\mathbf{q}}^{-1}$$
计算结果的实部为 0 , 故为纯虚四元数。其虚部的三个分量表 示旋转后 $3\mathrm{D}$ 点的坐标。

设四元数 $\mathbf{q}=q_0+q_{1}i+q_{2}j+q_{3}k$, 对应的旋转矩阵 $\mathbf{R}$ 为:
R = [ 1 − 2 q 2 2 − 2 q 3 2 2 q 1 q 2 + 2 q 0 q 3 2 q 1 q 3 − 2 q 0 q 2 2 q 1 q 2 − 2 q 0 q 3 1 − 2 q 1 2 − 2 q 3 2 2 q 2 q 3 + 2 q 0 q 1 2 q 1 q 3 + 2 q 0 q 2 2 q 2 q 3 − 2 q 0 q 1 1 − 2 q 1 2 − 2 q 2 2 ] \boldsymbol{R}=\left[

$$\begin{array}{lll} 1-2 q_{2}^{2}-2 q_{3}^{2} & 2 q_{1} q_{2}+2 q_{0} q_{3} & 2 q_{1} q_{3}-2 q_{0} q_{2} \\ 2 q_{1} q_{2}-2 q_{0} q_{3} & 1-2 q_{1}^{2}-2 q_{3}^{2} & 2 q_{2} q_{3}+2 q_{0} q_{1} \\ 2 q_{1} q_{3}+2 q_{0} q_{2} & 2 q_{2} q_{3}-2 q_{0} q_{1} & 1-2 q_{1}^{2}-2 q_{2}^{2} \end{array}$$ \right] R=⎣ ⎡​1−2q22​−2q32​2q1​q2​−2q0​q3​2q1​q3​+2q0​q2​​2q1​q2​+2q0​q3​1−2q12​−2q32​2q2​q3​−2q0​q1​​2q1​q3​−2q0​q2​2q2​q3​+2q0​q1​1−2q12​−2q22​​⎦ ⎤​
反之, 由旋转矩阵到四元数的转换如下。假设矩阵为 R = { m i j } , i , j ∈ [ 1 , 2 , 3 ] \boldsymbol R=\left\{m_{i j}\right\}, i, j \in[1,2,3] R={mij​},i,j∈[1,2,3], 其对 应的四元数 $q$ 由下式给出:
$$q_0=\frac{\sqrt{\mathrm{tr}(R)+1}}{2},q_1=\frac{m_{23}-m_{32}}{4q_0},q_2=\frac{m_{31}-m_{13}}{4q_0},q_3=\frac{m_{12}-m_{21}}{4q_0}.$$
值得一提的是, 由于 $\mathbf{q}$ 和 $-\mathbf{q}$ 表示同一个旋转, 事实上一个 $\mathbf{R}$ 对应的四元数表示并 不是惟一的。同时, 除了上面给出的转换方式之外, 还存在其他几种计算方法, 而本书都 省略了。实际編程中| 当 $q_0$ 接近 0 时, 其余三个分量会非常大, 导致解不稳定, 此时我们] 再考虑使用其他的方式进行转换。

李群和李代数基础

李群

前面介绍过，三位旋转矩阵构成了特殊正交群SO(3)，而变换矩阵构成了特殊欧式群SE(3)。我们可以观察到这两个"群"对于加法不封闭，二对于乘法封闭，换句话说就是：
$$R_1+R_2\notin SO(3)，R_1{R}_2\in SO(3),$$
我们首先介绍群（Group）的概念：是一种集合加上一种运算的代数结构。我们把集合记作 $A$, 运算记作 . , 那么群可以记作 $G=(A,\cdot )$ 。群要求这个运算满足以下几个条件:

1. 封闭性: $\forall a_1,a_2\in A,a_1\cdot a_2\in A$.
2. 结合律： $\forall a_1,a_2,a_3\in A,\left(a_1\cdot a_2\right)\cdot a_3=a_1\cdot \left(a_2\cdot a_3\right)$.
3. 么元: $\exists a_0\in A$, s.t. $\forall a\in A,a_0\cdot a=\alpha \cdot a_0=\alpha$.
4. 逆: $\forall a\in A,\exists a^{-1}\in A$, s.t. $a\cdot a^{-1}=a_0$.

矩阵中常见的群有：

• 一般线性群 GL(n) 指 n × n 的可逆矩阵，它们对矩阵乘法成群。
• 特殊正交群 SO(n) 也就是所谓的旋转矩阵群，其中 SO(2) 和SO(3) 最为常见。
• 特殊欧氏群 SE(n) 也就是前面提到的 n 维欧氏变换，如 SE(2) 和 SE(3)。
  李群是指具有连续（光滑）性质的群。像整数群 Z 那样离散的群没有连续性质，所以不是李群。而 SO(n) 和 SE(n)，它们在实数空间上是连续的。我们能够直观地想象一个刚体能够连续地在空间中运动，所以它们都是李群。

李代数

考虑任意旋转矩阵R，有

$$R{R}^T=I.$$
在等式两边对时间求导, 得到:
$$\dot{\mathbf{R}}(t)\mathbf{R}(t{)}^T+\mathbf{R}(t)\dot{\mathbf{R}}(t{)}^T=0.$$
整理得:
$$\dot{\mathbf{R}}(t)\mathbf{R}(t{)}^T=-{\left(\dot{\mathbf{R}}(t)\mathbf{R}(t{)}^T\right)}^T.$$
这里我们引入符号${}^{\vee }$，它与符号${}^{\wedge }$正相反，可以将反对称矩阵变成与之对应的向量。即
a ∧ = A = [ 0 − a 3 a 2 a 3 0 − a 1 − a 2 a 1 0 ] , A ∨ = a . \boldsymbol{a}^{\wedge}=\boldsymbol{A}=\left[

$$\begin{array}{ccc} 0 & -a_{3} & a_{2} \\ a_{3} & 0 & -a_{1} \\ -a_{2} & a_{1} & 0 \end{array}$$ \right], \quad \boldsymbol{A}^{\vee}=\boldsymbol{a} . a∧=A=⎣ ⎡​0a3​−a2​​−a3​0a1​​a2​−a1​0​⎦ ⎤​,A∨=a.
于是, 由于 $\dot{R}(t)\mathbf{R}(t{)}^T$ 是一个反对称矩阵, 我们可以找到一个三维向量 $\varphi (t)\in {\mathbb{R}}^3$ 与 之对应。于是有：
$$\dot{\mathbf{R}}(t)\mathbf{R}(t{)}^T=\varphi (t{)}^{\wedge }.$$
等式两边右乘 $R(t)$, 由于 $R$ 为正交阵, 有:
$$\dot{\mathbf{R}}(t)=\varphi (t{)}^{\wedge }\mathbf{R}(t)=\left[\begin{array}{ccc}0& -{\varphi }_3& {\varphi }_2\\ {\varphi }_3& 0& -{\varphi }_1\\ -{\varphi }_2& {\varphi }_1& 0\end{array}\right]\mathbf{R}(t).$$
可以看到, 每对旋转矩阵求一次导数, 只需左乘一个 ${\varphi }^{\wedge }(t)$ 矩阵即可。为方便讨论, 我 们设 $t_0=0$, 并设此时旋转矩阵为 $\mathbf{R}(0)=\mathbf{I}$ 。按照导数定义, 可以把 $\mathbf{R}(t)$ 在 0 附近进行 一阶泰勒展开:
$$\begin{array}{rl}\mathbf{R}(t)& \approx \mathbf{R}\left(t_0\right)+\dot{R}\left(t_0\right)\left(t-t_0\right)\\ & =\mathbf{I}+\varphi {\left(t_0\right)}^{\wedge }(t).\end{array}$$
我们看到 $\varphi$ 反应了 $\mathbf{R}$ 的导数性质, 故称它在 $SO(3)$ 原点附近的正切空间 (Tangent Space) 上。同时在 $t_0$ 附近, 设 $\varphi$ 保持为常数 $\varphi \left(t_0\right)={\varphi }_0$ 。则有
$$\dot{R}(t)=\varphi {\left(t_0\right)}^{\wedge }\mathbf{R}(t)={\varphi }_0^{\wedge }\mathbf{R}(t).$$
上式是一个关于 $R$ 的微分方程, 而且我们知道初始值 $R(0)=I$, 解之, 得:
$$R(t)=\exp \left({\varphi }_0^{\wedge }t\right).$$
每个李群都有与之对应的李代数。李代数描述了李群的局部性质。通用的李代数的定 义如下:
李代数由一个集合 $\mathbb{V}$, 一个数域 $\mathbb{F}$ 和一个二元运算 [,] 组成。如果它们满足以下几条 性质, 称 $(\mathbb{V},\mathbb{F},[,]$, 为一个李代数, 记作 $\mathfrak{g}$ 。

1. 尌闭性 $\forall X,Y\in \mathbb{V},[X,Y]\in \mathbb{V}$.
2. 双线性 $\forall \mathbf{X},\mathbf{Y},\mathbf{Z}\in \mathbb{V},a,b\in \mathbb{F}$, 有:
   $$[a\mathbf{X}+b\mathbf{Y},\mathbf{Z}]=a[\mathbf{X},\mathbf{Z}]+b[\mathbf{Y},\mathbf{Z}],[\mathbf{Z},a\mathbf{X}+b\mathbf{Y}]=a[\mathbf{Z},\mathbf{X}]+b[\mathbf{Z},\mathbf{Y}]$$
3. 自反性 $\forall X\in \mathbb{V},[X,X]=0$.
4. 雅可比等价 $\forall X,Y,Z\in \mathbb{V},[X,[Y,Z]]+[Z,[Y,X]]+[Y,[Z,X]]=0$.

其中二元运算被称为李括号。从表面上来看, 李代数所需要的性质还是拴多的。相比于群中的较为简单的二元运算, 李括号表达了两个元素的差异。它不要求结合律, 而要求 元素和自己做李括号之后为零的性质。作为例子, 三维向量 ${\mathbb{R}}^3$ 上定义的叉积 $\times$ 是一种李 括号, 因此 $\mathfrak{g}=\left({\mathbb{R}}^3,\mathbb{R},\times \right)$ 构成了一个李代数。读者可以尝试将叉积的性质代入到上面四 条性质中。

李代数 $\mathfrak{so}(3)$和 $\mathfrak{se}(3)$

之前提到的 $\varphi$，事实上是一种李代数。SO(3) 对应的李代数是定义在 R3上的向量，我们记作 $\varphi$。根据前面的推导，每个 $\varphi$都可以生成一个反对称矩阵
Φ = ϕ ∧ = [ 0 − ϕ 3 ϕ 2 ϕ 3 0 − ϕ 1 − ϕ 2 ϕ 1 0 ] ∈ R 3 × 3 \Phi=\phi^{\wedge}=\left[

$$\begin{array}{ccc} 0 & -\phi_{3} & \phi_{2} \\ \phi_{3} & 0 & -\phi_{1} \\ -\phi_{2} & \phi_{1} & 0 \end{array}$$ \right] \in \mathbb{R}^{3 \times 3} Φ=ϕ∧=⎣ ⎡​0ϕ3​−ϕ2​​−ϕ3​0ϕ1​​ϕ2​−ϕ1​0​⎦ ⎤​∈R3×3
在此定义下, 两个向量 ${\varphi }_1,{\varphi }_2$ 的李括号为:
$$\left[{\varphi }_1,{\varphi }_2\right]={\left({\Phi }_1{\Phi }_2-{\Phi }_2{\Phi }_1\right)}^{\vee }.$$
读者可以去验证该定义下的李括号满足上面的几条性质。由于 $\varphi$ 与反对称矩阵关系很 紧密, 在不引起歧义的情况下, 就说 $\mathfrak{so}(3)$的元素是 3 维向量或者 3 维反对称矩阵, 不加 区别:
$$s0(3)=\left\{\varphi \in {\mathbb{R}}^3,\Phi ={\varphi }^{\wedge }\in {\mathbb{R}}^{3\times 3}\right\}.$$
至此, 我们已消楚了 $\mathfrak{so}(3)$的内容。它们是一个由三维向量组成的集合, 每个向量对 应到一个反对称矩阵, 可以表达旋转矩阵的导数。它与 $SO(3)$ 的关系由指数映射给定:
$$\mathbf{R}=\exp \left({\varphi }^{\wedge }\right).$$
对于SE(3),他也有对应的李代数 $\mathfrak{se}(3)$：
$$\mathfrak{se}(3)=\left\{\xi =\left[\begin{array}{c}\rho \\ \varphi \end{array}\right]\in {\mathbb{R}}^6,\rho \in {\mathbb{R}}^3,\varphi \in \mathfrak{so}(3),{\xi }^{\wedge }=\left[\begin{array}{cc}{\varphi }^{\wedge }& \rho \\ 0^T& 0\end{array}\right]\in {\mathbb{R}}^{4\times 4}\right\}$$
我们把每个 $\mathfrak{se}(3)$ 元素记作 $\xi$, 它是一个六维向量。前三维为平移, 记作 $\rho$ : 后三维为 旋转, 记作 $\varphi$, 实质上是 $\mathfrak{so}(3)$ 元素。同时, 我们拓展了 ${}^{\wedge }$ 符号的含义。在 $\mathfrak{se}(3)$ 中, 同 样使用 $\wedge$ 符号, 将一个六维向量转换成四维矩阵, 但这里不再表示反对称。

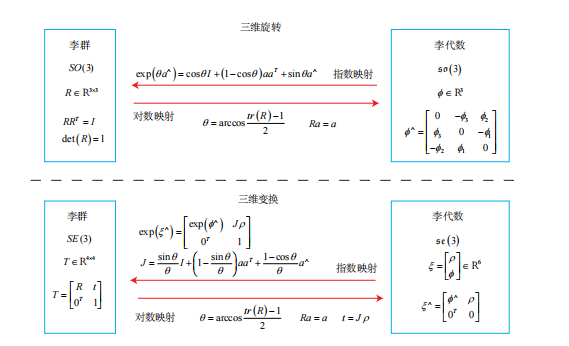
指数和对数映射

上文提到了指数矩阵$exp({\varphi }^{\wedge })$，在李群和李代数中又称为指数映射。那它到底该如何计算呢？这里我们直接给出结果：
$$\exp \left(\theta a^{\wedge }\right)=\cos \theta \mathbf{I}+(1-\cos \theta )\mathbf{a}{\mathbf{a}}^{\mathbf{T}}+\sin \theta {\mathbf{a}}^{\wedge }.$$
回忆前一讲内容, 它和罗德里格斯公式, 如出一辑。这表明, $\mathfrak{so}(3)$实际 上就是由所谓的旋转向量组成的空间, 而指数映射即罗德里格斯公式。通过它们, 我们把 $\mathfrak{se}(3)$中任意一个向量对应到了一个位于 $SO(3)$ 中的旋转矩阵。反之, 如果定义对数映射, 我们也能把 $SO(3)$ 中的元素对应到$\mathfrak{so}(3)$ 中:
$$\varphi =\ln (\mathbf{R}{)}^{\vee }={\left(\sum _{n=0}^{\infty }\frac{(-1{)}^n}{n+1}(\mathbf{R}-\mathbf{I}{)}^{n+1}\right)}^{\vee }.$$
不过我们通常不按照泰勒展开去计算对数映射。在介绍旋转的表示中，我们已经介绍过如何根据旋转矩阵计算对应的李代数，即利用迹的性质分别求解转角和转轴，采用那种方式更加省事一些。
同理，$\mathfrak{se}(3)$ 的指数映射形式如下：

BCH公式

虽然我们已经清楚了 SO(3) 和 SE(3)上的李群与李代数关系，但是，当我们在 SO(3) 中完成两个矩阵乘法时，李代数中 $s0(3)$ 上发生了什么改变呢？反过来说，当$s0(3)$ 上做两个李代数的加法时，SO(3) 上是否对应着两个矩阵的乘积？如果成立的话，相当于：
$$\ln (\exp (A)\exp (B))=A+B?$$
遗憾的是，这个式子对于A,B为标量时成立，但A,B若是矩阵，则不成立。两个李代数指数映射乘积的完整形式，由 Baker-Campbell-Hausdorff 公式（BCH 公式）给出。由于它完整的形式较复杂，我们给出它展开式的前几项：
$$\ln (\exp (A)\exp (B))=A+B+\frac{1}{2}[A,B]+\frac{1}{12}[A,[A,B]]-\frac{1}{12}[B,[A,B]]+\cdots$$
其中[]为李括号。 $\mathrm{BCH}$ 公式告诉我们, 当处理两个矩阵指数之积时, 它们会产生一些由 李括号组成的余项。特别地, 考虑 $SO(3)$ 上的李代数 $\ln {\left(\exp \left({\varphi }_1^{\wedge }\right)\exp \left({\varphi }_2^{\wedge }\right)\right)}^{\vee }$, 当 ${\varphi }_1$ 或 ${\varphi }_2$ 为小量时, 小量二次以上的项都可以被忽略掉。此时, $\mathrm{BCH}$ 拥有线性近似表达:
ln ⁡ ( exp ⁡ ( ϕ 1 ∧ ) exp ⁡ ( ϕ 2 ∧ ) ) ∨ ≈ { J 1 ( ϕ 2 ) − 1 ϕ 1 + ϕ 2  if  ϕ 1  is small,  J r ( ϕ 1 ) − 1 ϕ 2 + ϕ 1  if  ϕ 2  is small.  \ln \left(\exp \left(\phi_{1}^{\wedge}\right) \exp \left(\phi_{2}^{\wedge}\right)\right)^{\vee} \approx

$$\begin{cases}J_{1}\left(\phi_{2}\right)^{-1} \phi_{1}+\phi_{2} & \text { if } \phi_{1} \text { is small, } \\ J_{r}\left(\phi_{1}\right)^{-1} \phi_{2}+\phi_{1} & \text { if } \phi_{2} \text { is small. }\end{cases}$$ ln(exp(ϕ1∧​)exp(ϕ2∧​))∨≈{J1​(ϕ2​)−1ϕ1​+ϕ2​Jr​(ϕ1​)−1ϕ2​+ϕ1​​ if ϕ1​ is small,  if ϕ2​ is small. ​
以第一个近似为例。该式告诉我们，当对一个旋转矩阵 $R_2$ （李代数为 ${\varphi }_2$ ）左乘一个 微小旋转矩脌 $R_1$ (李代数为 ${\varphi }_1$ ）时，可以近似地看作，在原在的李代数 ${\varphi }_2$ 上, 加上了一 项 $J_l{\left({\varphi }_2\right)}^{-1}{\varphi }_1$ 。同理, 第二个近似描述了右乘一个微小位移的情况。于是, 李代数在 $\mathrm{BCH}$ 近似下，分成了左乘近似和右乘近似两种, 在使用时我们须加注意, 使用的是左乘模型还 是右韭模型。
本书以左乘为例。左乘 $\mathrm{BCH}$ 近似雅可比:
$$J_l=J=\frac{\sin \theta }{\theta }I+\left(1-\frac{\sin \theta }{\theta }\right)a{a}^T+\frac{1-\cos \theta }{\theta }{a}^{\wedge }.$$
它的逆为:
$$J_l^{-1}=\frac{\theta }{2}\cot \frac{\theta }{2}I+\left(1-\frac{\theta }{2}\cot \frac{\theta }{2}\right)a{a}^T-\frac{\theta }{2}{a}^{\wedge }.$$
而右乘雅可比仅需要对自变量取负号即可:
$$J_r(\varphi )=J_I(-\varphi ).$$
这样，我们就可以谈论李群乘法与李代数加法的关系了。假定对某个旋转 R，对应的李代数为 ϕ。我们给它左乘一个微小旋转，记作 ∆R，对应的李代数为 ∆ϕ。那么，在李群上，得到的结果就是 ∆R · R，而在李代数上，根据 BCH近似，为：Jl−1(ϕ)∆ϕ + ϕ。合并起来，可以简单地写成：
$$\exp \left(\Delta {\varphi }^{\wedge }\right)\exp \left({\varphi }^{\wedge }\right)=\exp \left({\left(\varphi +J_l^{-1}(\varphi )\Delta \varphi \right)}^{\wedge }\right)$$
反之, 如果我们在李代数上进行加法, 让一个 $\varphi$ 加上 $\Delta \varphi$, 那么可以近似为李群上带 左右雅可比的乘法:
$$\exp \left((\varphi +\Delta \varphi {)}^{\wedge }\right)=\exp \left({\left(J_l\Delta \varphi \right)}^{\wedge }\right)\exp \left({\varphi }^{\wedge }\right)=\exp \left({\varphi }^{\wedge }\right)\exp \left({\left({\mathbf{J}}_r\Delta \varphi \right)}^{\wedge }\right)$$
这将为之后李代数上的做微积分提供了理论基础。同样的, 对于 $SE(3)$, 亦有类似的 $\mathrm{BCH}$ 近似公式:
$$\begin{array}{rl}& \exp \left(\Delta {\xi }^{\wedge }\right)\exp \left({\xi }^{\wedge }\right)\approx \exp \left({\left({\mathcal{J}}_l^{-1}\Delta \xi +\xi \right)}^{\wedge }\right)\\ & \exp \left({\xi }^{\wedge }\right)\exp \left(\Delta {\xi }^{\wedge }\right)\approx \exp \left({\left({\mathcal{J}}_r^{-1}\Delta \xi +\xi \right)}^{\wedge }\right).\end{array}$$
这里 ${\mathcal{J}}_l$ 形式比较复杂, 它是一个 $6\times 6$ 的矩阵, 读者可以参考 [6] 中式 $(7.82)$ 和 (7.83) 内容。由于我们在计算中不用到该雅可比, 故这里略去它的实际形式。

李代数求导

在SLAM中，我们经常会构建与位姿有关的函数，然后讨论该函数关于
位姿的导数，以调整当前的估计值。所以讨论李代数的求导非常的重要，但是SO(3),SE(3)上没有良好定义的加法，他们只是群。如果我们把T当成一个普通矩阵来优化处理，那就必须对它加以约束，那就必须对它加以约束。而李代数是由向量组成的，具有良好的加法运算。因此使用李代数解决求导问题的思路分为两种：

• 用李代数表示姿态，然后对根据李代数加法来对李代数求导
• 对李群左乘或右乘微小扰动，然后对该扰动求导，成为左扰动和右扰动模型。

首先，考虑SO(3)的情况，假设对空间点p进行额旋转，得到Rp。宣布在要就算旋转后的点的坐标相对于旋转的导数，我们不严谨的记为：

$$\frac{\partial (\mathbf{R}\mathbf{p})}{\partial \mathbf{R}}$$
由于 $SO(3)$ 没有加法, 所以该导数无法按照导数的定义进行计算。设 $R$ 对应的李代数为 $\varphi$, 我们转而计算:
$$\frac{\partial \left(\exp \left({\varphi }^{\wedge }\right)p\right)}{\partial \varphi }$$
这里同样省略推到过程给出化简后的结果：
$$\frac{\partial (\mathbf{R}\mathbf{p})}{\partial \varphi }=(-\mathbf{R}\mathbf{p}{)}^{\wedge }{\mathbf{J}}_l.$$
不过，由于这里仍然含有形式比较复杂的 $J_l$，我们不太希望计算它。而下面要讲的扰动模型则提供了更简单的导数计算方式。

扰动模型

另一种求导方式, 是对 $\mathbf{R}$ 进行一次扰动 $\Delta \mathbf{R}$ 。这个扰动可以乘在左边也可以乘在右 边, 最后结果会有一点儿微小的差异, 我们以左扰动为例。设左扰动 $\Delta \mathbf{R}$ 对应的李代数为 $\phi$ 。然后, 对 $\phi$ 求导, 即:
$$\frac{\partial (\mathbf{Rp})}{\partial \phi }=\underset{\phi \to 0}{\lim }\frac{\exp \left({\phi }^{\wedge }\right)\exp \left({\varphi }^{\wedge }\right)p-\exp \left({\varphi }^{\wedge }\right)p}{\phi }.$$
该式的求导比上面更为简单:
∂ ( R p ) ∂ φ = lim ⁡ φ → 0 exp ⁡ ( φ ∧ ) exp ⁡ ( ϕ ∧ ) p − exp ⁡ ( ϕ ∧ ) p φ ≈ lim ⁡ φ → 0 ( 1 + φ ∧ ) exp ⁡ ( ϕ ∧ ) p − exp ⁡ ( ϕ ∧ ) p φ = lim ⁡ φ → 0 φ ∧ R p φ = lim ⁡ φ → 0 − ( R p ) ∧ φ φ = − ( R p ) ∧ .

$$\begin{aligned} \frac{\partial(R p)}{\partial \varphi} &=\lim _{\varphi \rightarrow 0} \frac{\exp \left(\varphi^{\wedge}\right) \exp \left(\phi^{\wedge}\right) p-\exp \left(\phi^{\wedge}\right) p}{\varphi} \\ & \approx \lim _{\varphi \rightarrow 0} \frac{\left(1+\varphi^{\wedge}\right) \exp \left(\phi^{\wedge}\right) p-\exp \left(\phi^{\wedge}\right) p}{\varphi} \\ &=\lim _{\varphi \rightarrow 0} \frac{\varphi^{\wedge} R p}{\varphi}=\lim _{\varphi \rightarrow 0} \frac{-(\boldsymbol{R} p)^{\wedge} \varphi}{\varphi}=-(\boldsymbol{R} p)^{\wedge} . \end{aligned}$$ ∂φ∂(Rp)​​=φ→0lim​φexp(φ∧)exp(ϕ∧)p−exp(ϕ∧)p​≈φ→0lim​φ(1+φ∧)exp(ϕ∧)p−exp(ϕ∧)p​=φ→0lim​φφ∧Rp​=φ→0lim​φ−(Rp)∧φ​=−(Rp)∧.​
可见, 扰动模型相比于直接对李代数求导, 省去了一个雅可比 $J_l$ 的计算。这使得扰动 模型更为实用。请读者务必理解这里的求导运算, 这在位姿估计当中具有重要的意义。
最后, 我们给出 $SE(3)$ 上的扰动模型, 而直接李代数上的求导就不再介绍了。假设 某空间点 $p$ 经过一次变换 $T$ (对应李代数为 $\xi$ ), 得到 $Tp$。现在, 给 $T$ 左乘一个扰动 $\Delta \mathbf{T}=\exp \left(\delta {\mathbf{\xi }}^{\wedge }\right)$, 我们设扰动项的李代数为 $\delta \xi =[\delta \rho ,\delta \varphi {]}^T$, 那么:
$\frac{\partial (\mathbf{T}\mathbf{p})}{\partial \delta \mathbf{\xi }}={\lim }_{\delta \mathbf{\xi }\to 0}\frac{\exp \left(\delta {\mathbf{\xi }}^{\wedge }\right)\exp \left({\mathbf{\xi }}^{\wedge }\right)p-\exp \left({\mathbf{\xi }}^{\wedge }\right)p}{\delta \mathbf{\xi }}$
$\approx {\lim }_{\delta \mathbf{\xi }\to 0}\frac{\left(\mathbf{I}+\delta {\mathbf{\xi }}^{\wedge }\right)\exp \left({\mathbf{\xi }}^{\wedge }\right)p-\exp \left({\mathbf{\xi }}^{\wedge }\right)\mathbf{p}}{\delta \mathbf{\xi }}$
$={\lim }_{\delta \mathbf{\xi }\to 0}\frac{\delta {\xi }^{\wedge }\exp \left({\xi }^{\wedge }\right)\mathbf{p}}{\delta \mathbf{\xi }}$
$={\lim }_{\delta \xi \to 0}\frac{\left[\begin{array}{cc}\delta {\varphi }^{\wedge }& \delta \rho \\ 0^T& 0\end{array}\right]\left[\begin{array}{c}\mathbf{Rp}+\mathbf{t}\\ 1\end{array}\right]}{\delta \xi }$
$={\lim }_{\delta \xi \to 0}\frac{\left[\begin{array}{c}\delta {\varphi }^{\wedge }(\mathbf{R}p+\mathbf{t})+\delta \mathbf{\rho }\\ 0\end{array}\right]}{\delta \xi }=\left[\begin{array}{cc}\mathbf{I}& -(\mathbf{R}p+\mathbf{t}{)}^{\wedge }\\ 0^T& 0^T\end{array}\right]\triangleq (\mathbf{T}\mathbf{p}{)}^{\odot }.$
我们把最后的结果定义成一个算符 $\odot$ 2), 它把一个齐次坐标的空间点变换成一个 $4\times 6$ 的矩阵。