一、推荐算法概述

对于推荐系统(Recommend System, RS)，从广义上的理解为：为用户(User)推荐相关的商品(Items)。常用的推荐算法主要有：

• 基于内容的推荐(Content-Based Recommendation)
• 协同过滤的推荐(Collaborative Filtering Recommendation)
• 基于关联规则的推荐(Association Rule-Based Recommendation)
• 基于效用的推荐(Utility-Based Recommendation)
• 基于知识的推荐(Knowledge-Based Recommendation)
• 组合推荐(Hybrid Recommendation)

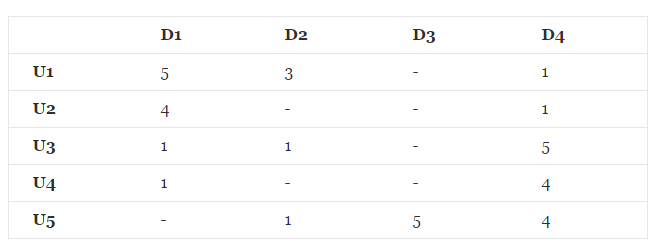
在推荐系统中，最重要的数据是用户对商品的打分数据，数据形式如下所示：

其中，$U_1\cdots U_5$表示的是$5$个不同的用户，$D_1\cdots D_4$表示的是$4$个不同的商品，这样便构成了用户-商品矩阵，在该矩阵中，有用户对每一件商品的打分，其中“-”表示的是用户未对该商品进行打分。

在推荐系统中有一类问题是对未打分的商品进行评分的预测。

二、基于矩阵分解的推荐算法

2.1、矩阵分解的一般形式

矩阵分解是指将一个矩阵分解成两个或者多个矩阵的乘积。对于上述的用户-商品矩阵(评分矩阵)，记为$R_{m\times n}$。可以将其分解成两个或者多个矩阵的乘积，假设分解成两个矩阵$P_{m\times k}$和$Q_{k\times n}$，我们要使得矩阵$P_{m\times k}$和$Q_{k\times n}$的乘积能够还原原始的矩阵$R_{m\times n}$：

$$R_{m\times n}\approx P_{m\times k}\times Q_{k\times n}=\hat{R}_{m\times n}$$

其中，矩阵$P_{m\times k}$表示的是$m$个用户与$k$个主题之间的关系，而矩阵$Q_{k\times n}$表示的是$k$个主题与$n$个商品之间的关系。

2.2、利用矩阵分解进行预测

在上述的矩阵分解的过程中，将原始的评分矩阵$R_{m\times n}$分解成两个矩阵$P_{m\times k}$和$Q_{k\times n}$的乘积：

$$R_{m\times n}\approx P_{m\times k}\times Q_{k\times n}=\hat{R}_{m\times n}$$

那么接下来的问题是如何求解矩阵$P_{m\times k}$和$Q_{k\times n}$的每一个元素，可以将这个问题转化成机器学习中的回归问题进行求解。

2.2.1、损失函数

可以使用原始的评分矩阵$R_{m\times n}$与重新构建的评分矩阵$\hat{R}_{m\times n}$之间的误差的平方作为损失函数，即：

$$e_{i,j}^2=\left ( r_{i,j}-\hat{r}_{i,j} \right )^2=\left (r_{i,j}-\sum_{k=1}^{K}p_{i,k}q_{k,j} \right )^2$$

最终，需要求解所有的非“-”项的损失之和的最小值：

$$min\; loss= \sum_{r_{i,j}\neq -}e_{i,j}^2$$

2.2.2、损失函数的求解

对于上述的平方损失函数，可以通过梯度下降法求解，梯度下降法的核心步骤是

• 求解损失函数的负梯度：

$$\frac{\partial }{\partial p_{i,k}}e_{i,j}^2=-2\left ( r_{i,j}-\sum_{k=1}^{K}p_{i,k}q_{k,j} \right )q_{k,j}=-2e_{i,j}q_{k,j}$$

$$\frac{\partial }{\partial q_{k,j}}e_{i,j}^2=-2\left ( r_{i,j}-\sum_{k=1}^{K}p_{i,k}q_{k,j} \right )p_{i,k}=-2e_{i,j}p_{i,k}$$

• 根据负梯度的方向更新变量：

$${p_{i,k}}'=p_{i,k}-\alpha \frac{\partial }{\partial p_{i,k}}e_{i,j}^2=p_{i,k}+2\alpha e_{i,j}q_{k,j}$$

$${q_{k,j}}'=q_{k,j}-\alpha \frac{\partial }{\partial q_{k,j}}e_{i,j}^2=q_{k,j}+2\alpha e_{i,j}p_{i,k}$$

通过迭代，直到算法最终收敛。

2.2.3、加入正则项的损失函数即求解方法

通常在求解的过程中，为了能够有较好的泛化能力，会在损失函数中加入正则项，以对参数进行约束，加入$L_2$正则的损失函数为：

$$E_{i,j}^2=\left (r_{i,j}-\sum_{k=1}^{K}p_{i,k}q_{k,j} \right )^2+\frac{\beta }{2}\sum_{k=1}^{K}\left ( p_{i,k}^2+q_{k,j}^2 \right )$$

利用梯度下降法的求解过程为：

• 求解损失函数的负梯度：

$$\frac{\partial }{\partial p_{i,k}}E_{i,j}^2=-2\left ( r_{i,j}-\sum_{k=1}^{K}p_{i,k}q_{k,j} \right )q_{k,j}+\beta p_{i,k}=-2e_{i,j}q_{k,j}+\beta p_{i,k}$$

$$\frac{\partial }{\partial q_{k,j}}E_{i,j}^2=-2\left ( r_{i,j}-\sum_{k=1}^{K}p_{i,k}q_{k,j} \right )p_{i,k}+\beta q_{k,j}=-2e_{i,j}p_{i,k}+\beta q_{k,j}$$

• 根据负梯度的方向更新变量：

$${p_{i,k}}'=p_{i,k}-\alpha \left ( \frac{\partial }{\partial p_{i,k}}e_{i,j}^2+\beta p_{i,k} \right )=p_{i,k}+\alpha \left ( 2e_{i,j}q_{k,j}-\beta p_{i,k} \right )$$

$${q_{k,j}}'=q_{k,j}-\alpha \left ( \frac{\partial }{\partial q_{k,j}}e_{i,j}^2+\beta q_{k,j} \right )=q_{k,j}+\alpha \left ( 2e_{i,j}p_{i,k}-\beta q_{k,j} \right )$$

通过迭代，直到算法最终收敛。

2.2.4、预测

利用上述的过程，我们可以得到矩阵$P_{m\times k}$和$Q_{k\times n}$，这样便可以为用户$i$对商品$j$进行打分：

$$\sum_{k=1}^{K}p_{i,k}q_{k,j}$$

2.3、程序实现

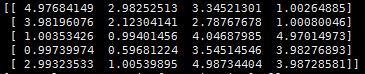
对于上述的评分矩阵，通过矩阵分解的方法对其未打分项进行预测，最终的结果为：

程序代码如下：

#!/bin/python
'''
Date:20160411
@author: zhaozhiyong
'''
from numpy import *

def load_data(path):
    f = open(path)
    data = []
    for line in f.readlines():
        arr = []
        lines = line.strip().split("\t")
        for x in lines:
            if x != "-":
                arr.append(float(x))
            else:
                arr.append(float(0))
        #print arr
        data.append(arr)
    #print data
    return data

def gradAscent(data, K):
    dataMat = mat(data)
    print dataMat
    m, n = shape(dataMat)
    p = mat(random.random((m, K)))
    q = mat(random.random((K, n)))

    alpha = 0.0002
    beta = 0.02
    maxCycles = 10000

    for step in xrange(maxCycles):
        for i in xrange(m):
            for j in xrange(n):
                if dataMat[i,j] > 0:
                    #print dataMat[i,j]
                    error = dataMat[i,j]
                    for k in xrange(K):
                        error = error - p[i,k]*q[k,j]
                    for k in xrange(K):
                        p[i,k] = p[i,k] + alpha * (2 * error * q[k,j] - beta * p[i,k])
                        q[k,j] = q[k,j] + alpha * (2 * error * p[i,k] - beta * q[k,j])

        loss = 0.0
        for i in xrange(m):
            for j in xrange(n):
                if dataMat[i,j] > 0:
                    error = 0.0
                    for k in xrange(K):
                        error = error + p[i,k]*q[k,j]
                    loss = (dataMat[i,j] - error) * (dataMat[i,j] - error)
                    for k in xrange(K):
                        loss = loss + beta * (p[i,k] * p[i,k] + q[k,j] * q[k,j]) / 2

        if loss < 0.001:
            break
        #print step
        if step % 1000 == 0:
            print loss

    return p, q


if __name__ == "__main__":
    dataMatrix = load_data("./data")

    p, q = gradAscent(dataMatrix, 5)
    '''
    p = mat(ones((4,10)))
    print p
    q = mat(ones((10,5)))
    '''
    result = p * q
    #print p
    #print q

    print result
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80

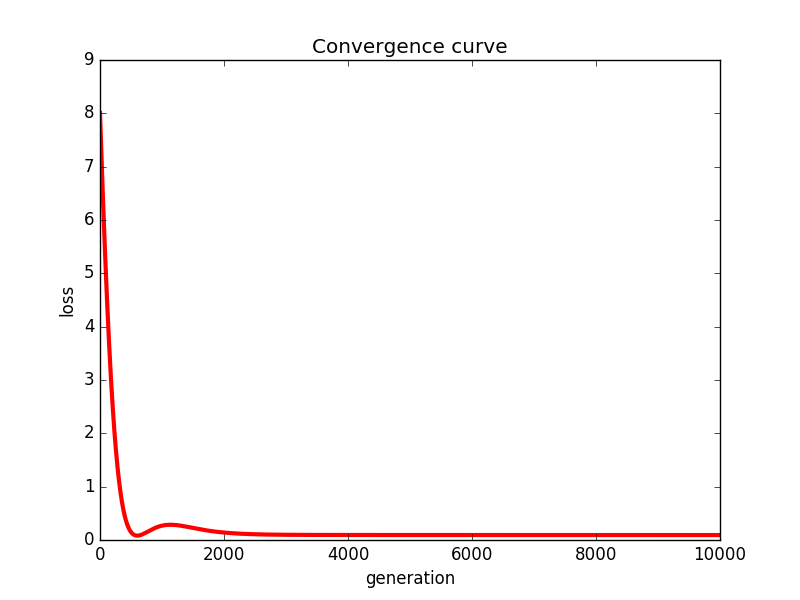
其中，利用梯度下降法进行矩阵分解的过程中的收敛曲线如下所示：

'''
Date:20160411
@author: zhaozhiyong
'''

from pylab import *
from numpy import *

data = []

f = open("result")
for line in f.readlines():
    lines = line.strip()
    data.append(lines)

n = len(data)
x = range(n)
plot(x, data, color='r',linewidth=3)
plt.title('Convergence curve')
plt.xlabel('generation')
plt.ylabel('loss')
show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

参考文献

• 《大数据智能》
• Matrix Factorization: A Simple Tutorial and Implementation in Python