损失函数：BCE Loss（二元交叉熵损失函数）、Dice Loss（Dice相似系数损失函数）

前言

• 由于本人水平有限，难免出现错漏，敬请批评改正。
• 更多精彩内容，可点击进入人工智能知识点专栏、Python日常小操作专栏、OpenCV-Python小应用专栏、YOLO系列专栏、自然语言处理专栏或我的个人主页查看
• 基于DETR的人脸伪装检测
• YOLOv7训练自己的数据集（口罩检测）
• YOLOv8训练自己的数据集（足球检测）
• YOLOv5：TensorRT加速YOLOv5模型推理
• YOLOv5：IoU、GIoU、DIoU、CIoU、EIoU
• 玩转Jetson Nano（五）：TensorRT加速YOLOv5目标检测
• YOLOv5：添加SE、CBAM、CoordAtt、ECA注意力机制
• YOLOv5：yolov5s.yaml配置文件解读、增加小目标检测层
• Python将COCO格式实例分割数据集转换为YOLO格式实例分割数据集
• YOLOv5：使用7.0版本训练自己的实例分割模型（车辆、行人、路标、车道线等实例分割）
• 使用Kaggle GPU资源免费体验Stable Diffusion开源项目

相关介绍

损失函数（Loss Function）在机器学习和深度学习中扮演着至关重要的角色，它是一个评估模型预测输出与真实标签之间差异程度的函数。损失函数量化了模型预测错误的程度，并在训练过程中作为优化的目标，模型通过不断地调整内部参数以最小化损失函数的值，从而实现更好的拟合数据和泛化能力。

主要特性与作用：

1. 量化误差：损失函数将模型预测值与实际目标值之间的差异转化为数值，这样就可以通过数值大小直观地衡量模型的预测效果。

2. 优化导向：在训练神经网络时，优化算法（如梯度下降法）会根据损失函数的梯度来更新模型参数，使损失函数朝着最小化方向移动。

3. 种类多样：根据不同的任务和需求，有多种不同的损失函数可供选择。例如，在二分类任务中常用的有二元交叉熵损失函数（Binary Cross-Entropy Loss/BCE Loss），在多分类任务中有softmax交叉熵损失函数，在回归任务中常见的是均方误差（Mean Squared Error/MSE）和绝对误差（Mean Absolute Error/MAE）等。

常见的损失函数包括：

• 二元交叉熵损失（Binary Cross-Entropy Loss / BCE Loss）：适用于二分类问题，衡量的是sigmoid函数输出的概率与真实标签间的距离。

• 多分类交叉熵损失（Categorical Cross-Entropy Loss）：对于多分类问题，每个样本可能属于多个类别之一，使用softmax函数和交叉熵损失。

• 均方误差（Mean Squared Error / MSE）：在回归问题中常用，计算预测值与真实值之差的平方平均。

• 均方根误差（Root Mean Squared Error / RMSE）：MSE的平方根，也是回归任务中的损失函数。

• Huber损失：一种既能兼顾均方误差又能容忍较大误差的混合损失函数，常用于回归问题中。

• Dice系数损失（Dice Loss）：在图像分割任务中广泛使用，衡量的是预测分割区域与真实分割区域的重叠程度。

• IoU（Intersection over Union）损失：也是在图像分割领域常用的损失函数，计算的是预测区域与真实区域交集与其并集的比例。

• Focal Loss：在目标检测中应对类别不平衡问题的损失函数，对易分类的样本给予较小的权重，强调难分类样本的训练。

每种损失函数都有其适用的情境和优缺点，选择合适的损失函数是优化模型性能的关键因素之一。

交叉熵（Cross-Entropy）之所以能够用于分类问题，是因为它能够很好地衡量模型预测的概率分布与实际标签分布之间的相似度，而且它拥有几个非常适合分类任务的重要特性：

1. 信息论基础：交叉熵源于信息论中的概念，表示一个概率分布 (p) 与另一个概率分布 (q) 的差异。在分类问题中，我们可以把 (p) 视为真实数据的标签分布，(q)视为模型预测的概率分布。交叉熵可以衡量模型预测概率与实际类别标签之间的信息差异。

2. 最大似然估计的自然延伸：在机器学习中，我们通常倾向于最大化模型对数据的似然性，即模型预测给定数据标签的概率。交叉熵损失函数实际上是负对数似然函数在多项式分布（对于多分类问题）或伯努利分布（对于二分类问题）下的特殊情况，通过最小化交叉熵损失，相当于最大化数据的对数似然性。

3. 梯度稳定性：交叉熵损失函数是连续且可微的，其梯度容易计算且对于大多数情况是有意义的。这意味着在训练过程中，模型可以根据损失函数的梯度进行有效的参数更新。

4. 稀疏性惩罚：对于多分类问题，softmax函数与交叉熵损失组合使用时，不仅鼓励模型正确预测每个样本的类别，同时也通过归一化机制惩罚了预测概率分布的不均匀性，即模型不能过于肯定任何一个错误类别。

5. 处理多类别和二类别问题：交叉熵既可以用于处理二分类问题（通过二元交叉熵，Binary Cross-Entropy），也可以处理多分类问题（通过多类别交叉熵，Multiclass
   Cross-Entropy）。在二分类问题中，通常搭配Sigmoid函数输出概率；在多分类问题中，通常配合Softmax函数生成类别概率分布。

总的来说，交叉熵损失函数因其良好的理论基础、优化目标清晰以及在实践中的优秀表现，成为了分类问题中最常用的损失函数之一。

BCE Loss（二元交叉熵损失函数）

Binary Cross-Entropy Loss，简称BCE Loss，是用于二分类问题的损失函数，特别适用于概率输出且标签只有两类（通常标记为0和1）的情况。在机器学习和深度学习中，当我们训练模型去预测一个事件发生的概率时，BCE Loss可以帮助我们衡量模型预测的概率分布与实际观测标签之间的差距，并以此作为优化模型的依据。

数学公式

对于单个样本，假设其真实标签 ( y ) 是一个二值变量，取值为0或1，而模型预测的概率 ( p )
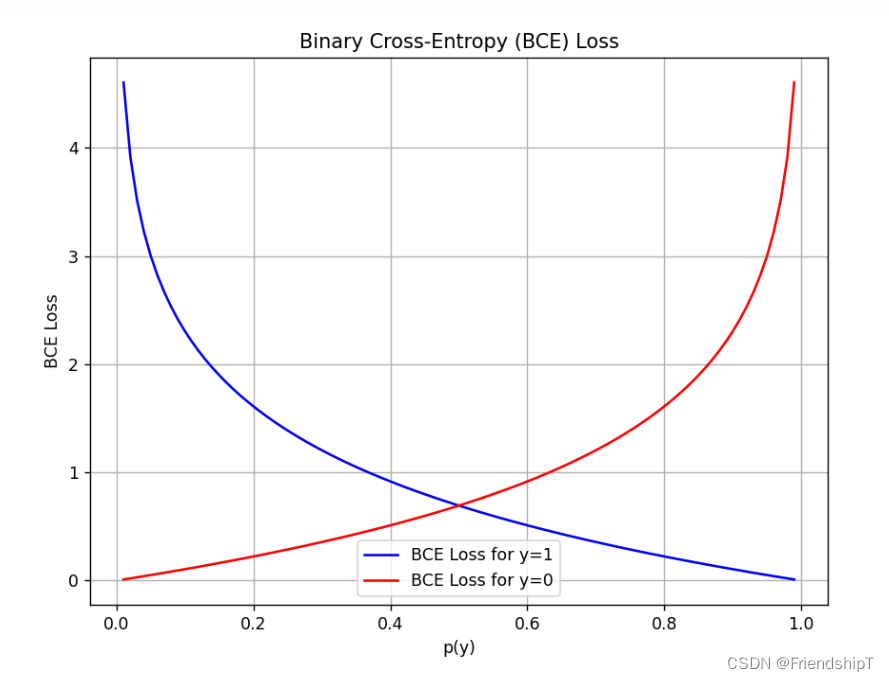
介于0和1之间，那么针对这一个样本的BCE Loss可以表示为：

$BCE(p,y)=-[y\log (p)+(1-y)\log (1-p)]$

• 当 ( y = 1 ) 时，真实标签表示事件发生，我们希望模型预测的概率 ( p ) 尽可能接近1，损失函数会惩罚 ( p ) 值偏低的情况。
• 当 ( y = 0 ) 时，真实标签表示事件未发生，我们希望模型预测的概率 ( p ) 尽可能接近0，损失函数会惩罚 ( p ) 值偏高的情况。

批量计算

对于一批样本，BCE Loss通常是对所有样本的BCE损失求和后除以样本数量（即平均损失）：

$BCE=-\frac{1}{N}{\sum }_{i=1}^N[y_i\log (p_i)+(1-y_i)\log (1-p_i)]$

这里的 ( N ) 是样本数量，( y_i ) 是第 ( i ) 个样本的真实标签，( p_i ) 是模型预测的第 ( i ) 个样本为正类的概率。

应用场景

BCE Loss广泛应用于各类二分类任务，如文本情感分析（积极/消极）、垃圾邮件检测（垃圾邮件/非垃圾邮件）、病患诊断（患病/未患病）等。在多标签分类任务中，如果每个样本的每个标签都可以独立看作一个二分类问题，那么也可以对每个标签分别计算BCE Loss，最终将所有标签的BCE Loss加权或相加得出总体损失。

特点

• BCE Loss能够很好地度量概率预测的准确性，当预测概率越接近真实标签值时，损失越小。
• 它能够促使模型对正负样本做出区分，并通过梯度下降等优化算法调整模型参数，使预测概率更加贴合实际标签。
  

代码实例

直接计算

import torch
from torch import autograd
input = autograd.Variable(torch.tensor([[ 1.9072,  1.1079,  1.4906],
                                                                                    [-0.6584, -0.0512,  0.7608],
                                                                                    [-0.0614,  0.6583,  0.1095]]), requires_grad=True)
from torch import nn
m = nn.Sigmoid()
target = torch.FloatTensor([[0, 1, 1], [1, 1, 1], [0, 0, 0]])

import math

r11 = 0 * math.log(0.8707) + (1-0) * math.log((1 - 0.8707))
r12 = 1 * math.log(0.7517) + (1-1) * math.log((1 - 0.7517))
r13 = 1 * math.log(0.8162) + (1-1) * math.log((1 - 0.8162))

r21 = 1 * math.log(0.3411) + (1-1) * math.log((1 - 0.3411))
r22 = 1 * math.log(0.4872) + (1-1) * math.log((1 - 0.4872))
r23 = 1 * math.log(0.6815) + (1-1) * math.log((1 - 0.6815))

r31 = 0 * math.log(0.4847) + (1-0) * math.log((1 - 0.4847))
r32 = 0 * math.log(0.6589) + (1-0) * math.log((1 - 0.6589))
r33 = 0 * math.log(0.5273) + (1-0) * math.log((1 - 0.5273))

r1 = -(r11 + r12 + r13) / 3
#0.8447112733378236
r2 = -(r21 + r22 + r23) / 3
#0.7260397266631787
r3 = -(r31 + r32 + r33) / 3
#0.8292933181294807
bceloss = (r1 + r2 + r3) / 3 
print(bceloss) # 0.8000147727101611
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

函数计算

import torch
from torch import autograd
input = autograd.Variable(torch.tensor([[ 1.9072,  1.1079,  1.4906],
                                                                                    [-0.6584, -0.0512,  0.7608],
                                                                                    [-0.0614,  0.6583,  0.1095]]), requires_grad=True)
from torch import nn
m = nn.Sigmoid()

target = torch.FloatTensor([[0, 1, 1], [1, 1, 1], [0, 0, 0]])

loss = nn.BCELoss()
print(loss(m(input), target)) # tensor(0.8000, grad_fn=<BinaryCrossEntropyBackward0>)

# WithLogits 就是先将输出结果经过sigmoid，再交叉熵
loss = nn.BCEWithLogitsLoss()
print(loss(input, target)) # tensor(0.8000, grad_fn=<BinaryCrossEntropyWithLogitsBackward0>)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

Dice Loss（Dice相似系数损失函数）

Dice Loss（Dice Coefficient Loss）是一种在图像分割任务中广泛使用的损失函数，特别适用于像素级别的二分类或多分类任务，如医疗图像分割。Dice系数原本是衡量两个集合相似度的一种指标，其值范围在0到1之间，值越接近1表示重叠程度越高，反之则表示重叠程度越低。

在深度学习图像分割任务中，Dice Loss是对Dice系数的负数进行最大化（因为优化目标通常是要最小化损失函数），使其能够更好地反映模型预测结果与真实标签之间的相似度。

数学公式

假设我们的模型预测结果为 ( P )（二维或三维张量，每个像素点对应一个预测类别概率），真实标签为 ( G
)（同样是二维或三维张量，每个像素点对应一个类别标签，通常为0或1）。对于二分类问题，Dice Loss的一般形式为：

$DiceLoss=1-\frac{2\times |P\cap G|}{|P|+|G|}$

这里，$|P\cap G|$表示预测结果与真实标签交集的像素数量，$|P|$ 和$|G|$分别表示预测结果和真实标签各自的像素数量。

为了便于计算，Dice Loss通常转换为更易于梯度传播的形式：

$DiceLoss=1-\frac{2{\sum }_i{P}_i{G}_i}{{\sum }_i(P_i^2+G_i)}$

其中，( P_{i} ) 和 ( G_{i} ) 分别表示预测结果和真实标签在第 ( i ) 个像素点上的值。

特点

• Dice Loss关注的是预测区域和真实区域之间的重叠面积，对分割边界附近的像素点敏感，有助于提高模型对边界位置的预测准确性。
• 相比于其他损失函数如交叉熵损失（Cross Entropy Loss），Dice Loss在数据不平衡（比如前景和背景像素极度不均衡）的情况下表现更好，因为它直接比较的是两个集合的相似度，而非像素级别的错误率。

总之，Dice Loss作为一种评价分割任务好坏的指标转化而成的损失函数，能够有效地引导模型优化分割结果，使之更贴近真实的标注区域。

代码实例

import numpy as np
import torch
import torch.nn.functional as F

def dice_coef(output, target):
    smooth = 1e-5

    output = torch.sigmoid(output).view(-1).data.cpu().numpy()
    target = target.view(-1).data.cpu().numpy()
    intersection = (output * target).sum()

    return (2. * intersection + smooth) / \
        (output.sum() + target.sum() + smooth)
　
if __name__=="__main__":
    input = torch.tensor([[ 1.9072,  1.1079,  1.4906],
                                                [-0.6584, -0.0512,  0.7608],
                                                [-0.0614,  0.6583,  0.1095]])
    target = torch.tensor([[0., 1., 1.],
                                                 [1., 1., 1.],
                                                 [0., 0., 0.]])
    

    dice = dice_coef(input, target)
    print(dice) # 0.5796486165541632
    dice_loss = 1 - dice
    print(dice_loss) # 0.4203513834458368
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

• 由于本人水平有限，难免出现错漏，敬请批评改正。
• 更多精彩内容，可点击进入人工智能知识点专栏、Python日常小操作专栏、OpenCV-Python小应用专栏、YOLO系列专栏、自然语言处理专栏或我的个人主页查看
• 基于DETR的人脸伪装检测
• YOLOv7训练自己的数据集（口罩检测）
• YOLOv8训练自己的数据集（足球检测）
• YOLOv5：TensorRT加速YOLOv5模型推理
• YOLOv5：IoU、GIoU、DIoU、CIoU、EIoU
• 玩转Jetson Nano（五）：TensorRT加速YOLOv5目标检测
• YOLOv5：添加SE、CBAM、CoordAtt、ECA注意力机制
• YOLOv5：yolov5s.yaml配置文件解读、增加小目标检测层
• Python将COCO格式实例分割数据集转换为YOLO格式实例分割数据集
• YOLOv5：使用7.0版本训练自己的实例分割模型（车辆、行人、路标、车道线等实例分割）
• 使用Kaggle GPU资源免费体验Stable Diffusion开源项目