【数据结构】08排序

1. 冒泡排序（BubbleSort）

冒泡排序是一种交换排序，基本思想是：两两比较相邻记录的关键字，如果反序则交换，直到没有反序为止。

1.1 循环嵌套实现

// 循环嵌套实现
// len是元素个数
void BubbleSort1(int* arr, int len)
{
	for (int i = len - 1; i > 0; i--) // 比较len-1趟
	{
		// 每趟比较n-1个数据
		for (int j = 0; j < i; j++) // 只需要比较0,1,2,..,i之间的数据i之后的元素是已经排好序了
		{
			if (arr[j] > arr[j + 1])
			{
				int tmp = arr[j + 1];
				arr[j + 1] = arr[j];
				arr[j] = tmp;
			}
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

1.2 递归实现

每层递归中比较前n-1个元素，一共递归n趟

// 递归实现
void BubbleSort2(int* arr, int len)
{
	if (len < 2) // 元素为1个或0个不需要排序
	{
		return;
	}
	for (int i = 0; i < len - 1; i++)// 每趟比较0,1,...,n-1
	{
		if (arr[i] > arr[i + 1])
		{
			int tmp = arr[i + 1];
			arr[i + 1] = arr[i];
			arr[i] = tmp;
		}
	}
	BubbleSort2(arr, --len); // 下一趟
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

2. 选择排序

从头到尾扫描序列，找出最小的一个元素，和第一个元素做交换，接着从剩下的元素中继续这种选择和交换的方式，最终得到一个有序序列。

2.1 嵌套循环实现

// 循环嵌套实现选择排序
void SelectSort1(int* arr, int len)
{
	int i ;
	for (i = 0; i < len - 1; i++) // 一共需要len-1趟比较
	{
		int index =i; 
		for (int j = i + 1; j < len; j++) // 每趟需要比较i+1,i+2,....,len-1之间的元素，i之前的元素是排序好的
		{
			if (arr[j] < arr[index])  //记录最小值的位置
			{
				index = j;
			}
		}
		// 找到最小值,如不过不是第一个元素，则交换第一个元素和最小值
		if (index != i)
		{
			int tmp = arr[index];
			arr[index] = arr[i];
			arr[i] = tmp;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

2.2 递归实现

// 递归实现选择排序
void SelectSort2(int* arr, int len)
{
	if (len < 2) // 1个或两个元素不需要排序
	{
		return;
	}
	// 每趟循环需要找出最小值位置
	int index = 0;
	for (int i = 1; i < len; i++)
	{
		if (arr[i] < arr[index]) // 记录最小值位置
		{
			index = i;
		}
	}
	if (index != 0) // 交换首个元素和最小值
	{
		int tmp = arr[index];
		arr[index] = arr[0];
		arr[0] = tmp;
	}
	SelectSort2(arr + 1, --len);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

3. 插入排序

插入排序原理：通过构建有序序列，对未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

// 插入排序
void InsertSort(int* arr, int len)
{
	int i,j = 0;

	for (i = 1; i < len; i++)// 对第一个数不需要排序,从第二个数开始，从后向前比较
	{
		int tmp = arr[i]; // 待排序元素,已经排序元素为arr[0]~arr[i-1]
		for (j = i - 1; j >= 0; j--) // 从已经排序好的元素的最右边开始，从后向前遍历
		{
			if (arr[j] <=tmp) // 找到小于当前元素则不需要再后移了，此时需要插入到小于当前元素之后的一位
			{
				break;
			}
			// 把大于当前待排序元素的元素后移
			arr[j + 1] = arr[j];
		}
		// 插入当前元素
		arr[j + 1] = tmp;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

4. 希尔排序

希尔排序（Shell）是插入排序的一种，它是针对直接插入排序算法的改进。希尔排序的基本思想：把待排序的数列分成多个组，然后对每个组进行插入排序，先让数列整体大致有序，然后多次调整分组方式，使数列更加有序，最后再使用一次插入排序，整个数列将全部有序。
流程：

• 初始
  
• 分组
• 对每个组进行插入排序
  
• 调整元素间隔，重新分组，并对每组进行插入排序
  
• 调整元素间隔，重新分组，并对每组进行插入排序
  
  希尔排序的核心思想是化远为近：1）查找次数减少；2）移动元素次数减少

4.1 代码实现

希尔排序是在插入排序的基础上，每次取固定步长的间隔组成的分组，在其中进行插入排序。具体代码实现

// 间隔step执行插入排序
// start_pos每组的起始位置
// step 每组每个元素之间间隔的步长
void GroupSort(int* arr, int len, int start_pos, int step)
{
	int i=0, j=0;
	for (i = start_pos + step; i < len; i += step) // arr[start_pos]是第一个元素，跳过，从第二个开始即start_pos+step
	{
		int tmp = arr[i];//待排序袁旭，其中 arr[start_pos]，...,arr[start_pos+step*(i-1)]是排序好的
		for (j = i - step; j >= 0; j -= step)// 从后往前组内进行插入排序
		{
			if (arr[j] <= tmp)
			{
				break;
			}
			arr[j + step] = arr[j]; // 组内右移元素
		}
		// 插入当前元素
		arr[j + step] = tmp;
	}
}

void ShellSort(int* arr, int len)
{
	// step是步长，每次都为原来的一半取整数，最后一次必定为1
	for (int step = len / 2; step > 0; step = step / 2)
	{
		// 此时分为了step个组，对step个组内进行间隔step之间的元素插入排序
		for (int j = 0; j < step; j++)
		{
			GroupSort(arr, len, j, step);
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

5. 快速排序

快速排序的基本思想是：

1. 先从数列中取出一个元素作为基准数
2. 扫描数列，将比基准数小的元素放在它的左边，大于或等于基准数的元素全部放到它的右边，得到左右两个区间
3. 再对左右区间重复第1，2步，直到各个区间小于两个元素
   流程：挖坑填数+分治思想

• 初始化
  

• 这里以左指针指向的第一个为基准数，以右指针指向的第一个数开始扫描数组：1<4，将它插入到4左指针指向的位置；移动左指针
  
  

• 3<4，继续移动左指针；5>4，将5填入到右指针指向的位置；移动右指针，7>4，继续移动右指针，指向2
  

• 2<4 将2填入到左指针指向位置，移动左指针，左指针指向6,6>4，将6填入到右指针指向的位置，移动右指针
  
  

• 此时左指针和右指针重叠，把基准元素插入到左右指针指向的位置。

• 下一次比较从当前基准数的左区间和右区间分别开始迭代。
  

可以看到快速排序算法需要维护左指针，右指针，维护基准数。

5.1 代码实现

具体的代码实现如下：

void QuickSort(int* arr, int len)
{
	if (len < 2)
	{
		return;
	}

	int tmp = arr[0];	// 选取最左边的数作为基准数
	int left = 0; // 左下标
	int right = len - 1; // 右下标
	int moving_flag = 2; // 移动左下标还是右下标标志
	while (left < right)
	{
		if (moving_flag == 2) // 移动右下标
		{
			if (arr[right] >= tmp) // 大于基准数,则继续移动右下标
			{
				right--;
				continue;
			}	

			// 小于基准数，把它填入到左下标对应的坑中
			arr[left] = arr[right];
			// 左下标移动
			left++;
			// 下次将继续移动左下标
			moving_flag = 1;
			continue;
		}
		if (moving_flag == 1) // 移动左下标
		{
			if (arr[left] < tmp) // 小于基准数,则继续移动左下标
			{
				left++;
				continue;
			}
			// 大于基准数，把它填入到右下标对应的坑中
			arr[right] = arr[left];
			// 移动右下标
			right--;
			moving_flag = 2;// 下次移动右下标
			continue;
		}
	}
	// 循环结束，左右下标重合，填入基准数的值
	arr[left] = tmp;
	// 对基准数左边区间进行排序
	QuickSort(arr, left);
	// 对基准数右边区间进行排序
	QuickSort(arr + left + 1, len - left - 1);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

6. 归并排序

归并排序（Merge Sort）就是将已经有序的子数列合并得到另一个有序的数列。
归是归并的归，不是递归，归并排序就是合并排序。
流程：

• 初始化
  
  

• 归并排序
  

• 继续归并
  

• 最终结果
  

6.1 递归实现

流程：

代码

// 利用递归实现归并排序
// arr是待排序数组
// arr_tmp是用于排序的临时数组的首地址
// start是排序区间第一个元素的位置
// end是排序区间最后一个元素的位置
void _mergeSort(int* arr,int* arr_tmp, int start,int end)
{
	if (start >= end) // 表示该区间的元素少于两个，递归终止
	{
		return;
	}
	int mid = (start + end) / 2; // 计算排序区中间的位置

	int start1 = start, end1 = mid; // 左区间
	int start2 = mid + 1, end2 = end;// 右区间

	_mergeSort(arr, arr_tmp, start1, end1); // 对左边区间进行递归拆分
	_mergeSort(arr, arr_tmp, start2, end2); // 对右边区间进行递归拆分

	// 对区间内的元素进行合并排序
	// 把区间左右两边合并到已经排序数组arr_tmp中
	// 从arr_tmp的start开始
	int i = start;
	while (start1 <= end1 && start2 <= end2)
	{
		arr_tmp[i++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];
	}
	while (start1 <= end1) // 把左边剩下的追加到arr_tmp;
	{
		arr_tmp[i++] = arr[start1++];
	}
	while (start2 <= end2) // 把右边剩下的追加到arr_tmp
	{
		arr_tmp[i++] = arr[start2++];
	}
	// 把已经排序好的数组，复制到arr中
	memcpy(arr+start, arr_tmp+start, sizeof(int) * (end - start + 1));
}


void MergeSort(int* arr, int len)
{
	// 创建临时数组
	int* arr_tmp = new int[len];
	memset(arr_tmp, 0, sizeof(int) * len);
	_mergeSort(arr, arr_tmp, 0, len - 1);
	delete[]arr_tmp;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

6.2 循环实现

// 利用循环实现归并排序
void mergeSort(int* arr, int len)
{
	// 创建临时数组，用于存放已排序元素
	int* arr_tmp = new int[len];
	memset(arr_tmp, 0, sizeof(int) * len);

	for (int i = 1; i < len; i = i * 2) // 每趟选取i个元素作为左右区间
	{
		for (int j = 0; j < len; j = j + i * 2) // 把len长度按照i*2 拆分
		{
			int start = j; // 起始
			int mid = min(start + i, len); // 中间 ，考虑分配不均
			int end = min(start + i * 2, len); // 结尾，考虑分配不均的情况

			int k = start;
			int start1 = start, end1 = mid;
			int start2 = mid, end2 = end;
			while (start1 < end1 && start2 < end2)
			{
				arr_tmp[k++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];
			}
			// 把左边剩余元素追加
			while (start1 < end1)
			{
				arr_tmp[k++] = arr[start1++];
			}
			// 把右边剩余元素追加
			while (start2 < end2)
			{
				arr_tmp[k++] = arr[start2++];
			}
		}
		int* ptr_tmp = arr;
		arr = arr_tmp;
		arr_tmp = ptr_tmp;
	}

	if (arr!=arr_tmp)
	{
		memcpy(arr, arr_tmp, sizeof(int) * len);
	}
	delete [] arr_tmp;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

7. 堆排序

堆排序是利用堆这种数据结构而设计的一种排序算法，堆具备以下的特点：

• 完全二叉树（从上到下，从左到右都是满的，最后一层的结点都连续集中在最左边），对于用数组存储的完全二叉树有：N[i]的左子结点N[2i+1]，右子结点N[2i+2]，父结点N[(i-1)/2]
• 二叉树每个结点的值都大于等于其左右子树结点的值称为大顶堆；或者每个结点的值都小于等于其左右子树结点的值称为小顶堆。
  

7.1 构建大顶堆

流程：
首先利用heapify即元素下沉的方法，从最后一个元素的父结点开始，不断下沉小元素，构建一个大顶堆

• 比较结点的两个子结点，如果结点值都大于两个子结点，则不交换。不断向前
  
• 比较两个子结点，如果结点值小于子结点，取子结点最大值的那个结点与结点交换。并对交换后的结点进行同样的操作。
  如图中所示，结点0的左子结点和右子结点都大于0，取最大的那个结点即6，与0交换。此时0没有左子结点和右子结点则完成。
  
• 比较两个子结点，如果结点值小于子结点，取子结点最大值的那个结点与结点交换。并对交换后的结点进行同样的操作。
  如图中所示，结点1小于结点8，交换两个结点。之后继续比较结点的左子结点和右子节点，此时两个子结点都大于1，取最大的子结点7，交换。
  

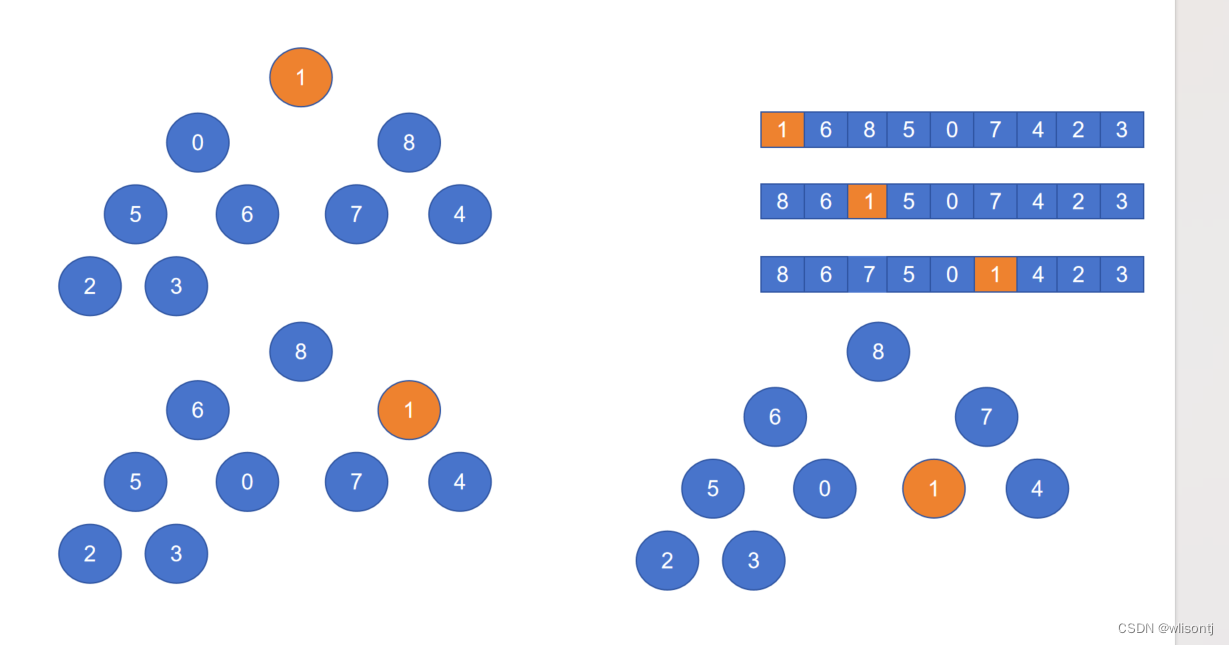
此时已经完成了所有结点的比较，构建出了一个大顶堆。可以看到8>6,8>7,6>5,6>0,7>1,7>4,5>2,5>3。

用循环实现heapify操作

void Swap(int* elem1, int* elem2)
{
	int tmp = *elem2;
	*elem2 = *elem1;
	*elem1 = tmp;
}
// 元素下沉
// 待排序数组地址，start-待下沉元素结点的下标，end待排序数组最后一个元素的下标
void heapify(int* arr, int start, int end)
{
	// 确定下沉结点和左子结点位置
	int parent = start;
	int son = 2 * start + 1; // 先比较左子结点

	while (son <= end)// 下标不越界
	{
		// 比较两个子结点的大小
		if ((son+1 <= end) && (arr[son] < arr[son+1])) // 右子结点存在 且 左子结点小于右子结点
		{
			son++; // 两个子节点中大的是右子节点
		}
		if (arr[parent] > arr[son]) // 比左右子结点都大，则不需要交换元素
		{
			return;
		}

		Swap(&arr[parent], &arr[son]); // 交换父子结点内容
		
		parent = son; // 继续向下
		son = 2 * parent + 1; // 左子结点
	}
}

void HeapSort(int* arr, int len)
{
	// 从最后一个元素的父结点开始初始化堆
	for (int i = (len - 1) / 2; i >= 0; i--)
	{
		heapify(arr, i, len - 1);
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

用递归实现heapify操作

// 递归实现heapify
void heapify2(int* arr, int start, int end)
{
	// 确定下沉结点和左子结点位置
	int parent = start;
	int son = 2 * start + 1;
	
	if (son > end)
	{
		return;
	}
	if ((son + 1 <= end) && arr[son] < arr[son + 1]) // 选择左右子结点最大的
	{
		son = son + 1;
	}

	if (arr[parent] > arr[son]) // 待下沉结点比左右子结点都大，无需下沉
	{
		return;
	}

	// 交换父结点与大的子结点
	Swap(&arr[parent], &arr[son]);
	// 对子结点进行heapify
	heapify2(arr, son, end);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

7.2 堆排序

在将数组初始化为大顶堆之后，交换首个元素与待排序数组的最后一个元素的位置（此时带排序数组的最后一个元素一定是最大的元素），并从交换后的首个元素进行下沉操作，除掉交换后的最后一个元素，构建大顶堆，如此循环。

7.3 代码实现

void Swap(int* elem1, int* elem2)
{
	int tmp = *elem2;
	*elem2 = *elem1;
	*elem1 = tmp;
}

// 元素下沉
// 待排序数组地址，start-待下沉元素结点的下标，end待排序数组最后一个元素的下标
void heapify(int* arr, int start, int end)
{
	// 确定下沉结点和左子结点位置
	int parent = start;
	int son = 2 * start + 1;

	while (son <= end)// 下标不越界
	{
		// 比较两个子结点的大小
		if ((son+1 <= end) && (arr[son] < arr[son+1])) // 右子结点存在 且 左子结点小于右子结点
		{
			son++; // 两个子节点中大的是右子节点
		}
		if (arr[parent] > arr[son]) // 比左右子结点都大，调整完毕
		{
			return;
		}

		Swap(&arr[parent], &arr[son]); // 否则交换父子结点内容
		
		parent = son; // 继续向下
		son = 2 * parent + 1;
	}
}


// 堆排序
void HeapSort(int* arr, int len)
{
	// 从最后一个元素的父结点开始初始化堆
	for (int i = (len - 1) / 2; i >= 0; i--)
	{
		heapify(arr, i, len - 1);
	}
	for (int i = 0; i < len; i++)
	{
		cout << arr[i] << " ";
	}
	cout << endl;
	// 把待排序数组第一个元素和最后一个元素交换，并从第一个元素开始进行下沉操作
	for (int i = len - 1; i > 0; i--)
	{
		Swap(&arr[0], &arr[i]);
		heapify(arr, 0, i - 1);
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

8. 计数排序

计数排序原理很简单，申请一个计数数组，遍历待排序数组，对每个出现的数据元素在计数数组的对应下标进行计数。遍历完成后，根据计数数组计数个数，对数据进行还原。
代码实现：

// 获取数组中最大元素的值
int array_max(int* arr, int len)
{
	int max_elem = arr[0];
	for (int i = 1; i < len; i++)
	{
		if (arr[i] > max_elem)
			max_elem = arr[i];
	}
	return max_elem;
}

void CountSort(int* arr, int len)
{
	int max_elem = array_max(arr, len);
	int* arr_tmp = new int[max_elem + 1];
	memset(arr_tmp, 0, sizeof(int) * (max_elem + 1));

	// 计数
	for (int i = 0; i < len; i++)
	{
		arr_tmp[arr[i]]++;// arr_tmp[arr[i]]的计数值++
	}
	
	// 重新填充
	int ii = 0;
	for (int j = 0; j < max_elem + 1; j++) // 遍历arr_tmp，下标对应的就是原数组的元素
	{
		for (int k = 0; k < arr_tmp[j]; k++) // 填充arr_tmp[jj]个
		{
			arr[ii++] = j;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

9. 桶排序

桶排序（BucketSort）的原理：假设输入数据服从均匀分布，将数据分到有限数量的桶里，然后再对每个桶分别排序(可以使用冒泡排序，快速排序等排序方法)，最后把全部桶的数据合并。

void BubbleSort(int* arr, int len)
{
	for (int i = len - 1; i > 0; i--) // 比较len-1趟
	{
		// 每趟比较n-1个数据
		for (int j = 0; j < i; j++) // 只需要比较0,1,2,..,i之间的数据i之后的元素是已经排好序了
		{
			if (arr[j] > arr[j + 1])
			{
				int tmp = arr[j + 1];
				arr[j + 1] = arr[j];
				arr[j] = tmp;
			}
		}
	}
}

void BucketSort(int* arr, int len)
{
	int bucket[5][5];  // 分配5个桶，实际按照数据大小调整，每个桶最多五个元素
	int bucketsize[5]; // 每个桶中的元素个数计数

	memset(bucket, 0, sizeof(bucket));
	memset(bucketsize, 0, sizeof(bucketsize));

	// 把数据arr放入桶中
	for (int i = 0; i < len; i++)
	{
		bucket[arr[i] / 10][bucketsize[arr[i] / 10]++] = arr[i];
	}
	// 对每个桶中的数据进行快速排序
	for (int i = 0; i < 5; i++)
	{
		BubbleSort(bucket[i], bucketsize[i]);
	}
	// 再把每个桶中的数据填充到arr中
	int k = 0;
	for (int i = 0; i < 5; i++)
	{
		for (int j = 0; j < bucketsize[i]; j++)
		{
			arr[k++] = bucket[i][j];
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

10. 基数排序

基数排序（Radix Sort）是桶排序的扩展，它的基本思想是：将整数按位数切割成不同的数字，然后按每个位数分别比较。
具体做法是：将所有带比较数字统一为一样的数位长度，数位较短的数前面补零。然后从最低位开始，依次进行一次排序。这样从最低位排序一直到最高位排序完成以后，就变成了一个有序数列。

• 第一次分配和收集
  
• 第二次分配和收集
  
• 第三次分配和收集
  

10.1 代码实现

// 获取最大元素
int getMax(int* arr, int len)
{
	int max_elem = arr[0];
	for (int i = 1; i < len; i++)
	{
		if (arr[i] > max_elem)
		{
			max_elem = arr[i];
		}
	}
	return max_elem;
}

// 按base位进行分配
void _radixsort(int* arr, int len, int base)
{
	int* arr_tmp = new int[len];
	memset(arr_tmp, 0, sizeof(int) * len);
	int bucket[10] = { 0 }; // 初始化桶0，1，2，...，9
	for (int i = 0; i < len; i++) // 按位数计数
	{
		bucket[arr[i] / base % 10] ++;
	}
	// 累加bucket
	for (int i = 1; i < 10; i++)
	{
		bucket[i] = bucket[i] + bucket[i - 1];
	}
	// 存放
	for (int i = len - 1; i >= 0; i--)
	{
		arr_tmp[bucket[arr[i] / base % 10] - 1] = arr[i];
		bucket[arr[i] / base % 10]--;
	}
	memcpy(arr, arr_tmp, sizeof(int) * len);
	delete[] arr_tmp;
}

void RadixSort(int* arr, int len)
{
	// 获取最大数值,决定分配收集的次数
	int max_elem = getMax(arr, len);
	int base = 1; // 从个位开始
	while (max_elem / base != 0)
	{
		_radixsort(arr, len, base);
		base = base * 10; // 向前一位
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50