【自然语言处理】【细粒度情感分析】细粒度情感分析：了解文本情感的What、How、Why

细粒度情感分析：了解文本情感的What、How、Why Knowing What,How and Way：A Near Complete Solution for Aspect-based Sentiment Analysis

论文地址：https://arxiv.org/pdf/1911.01616.pdf

一、细粒度情感分析

​ 细粒度情感分析任务ABSA(Aspect Based Sentiment Analysis)的目标是解决各类情感分析任务，其包括任务ATE(Aspect Term Extraction)、OTE(Opinion Term Extraction)和ATC(Aspect Term Sentiment Classification)。举例说明一下这些任务。给定一个例句
$$\text{Waiters are very friendly and the pasta is simply average.}$$
ATE的目标是抽取$\text{Waiters}$和$\text{pasta}$，ATC的目标是为ATE抽取出的aspect进行情感分类，OTE是抽取导致情感极性的词$\text{friendly}$和$\text{average}$。

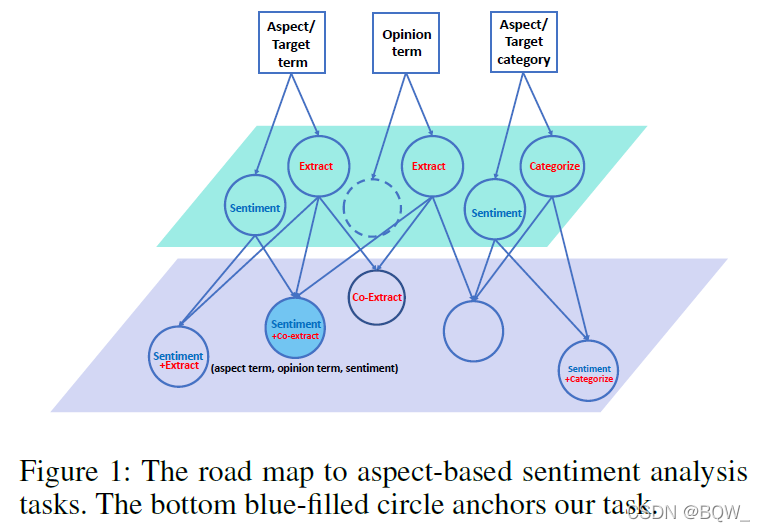
​ 虽然这几个任务看起来容易混淆，但是任务边界其实十分清晰。如下图所示，顶上的三个正方形表示ABSA的三个目标，其中aspect term表示需要句子中要目前讨论的目标(waiter)，opinion term表示评论观点的术语或者短语(friendly)，aspect category表示将aspect分类到预先定义的类别，例如“服务”或者“食物”。

​ 中间层的圆圈表示具体的子任务。研究人员认为独立去解决这些子任务是不够的，提出了两两成对解决这些子任务。但是，这样仍然不足以完成的描绘出整个情感的状态。例如，先前的例子中，能够确定$\text{waiters}$是正向情感，但是无法给出为什么是正向的线索，只有确定了$\text{friendly}$，才能真正理解导致情感正向的原因。Fan等人提出给定aspect，抽取对应opinion term的任务，该任务并不会预测情感。联合抽取aspect和opinion的任务也并不能解决二者间配对的问题。aspect抽取和情感分类联合任务中不能为aspect抽取opinion term。综合分析这些子任务的缺陷，论文提出了新的子任务ASTE(Aspect Sentiment Triplet Extraction)，其在所有子任务中的位置如下图中的实心圆。

二、方法简介

​ 新子任务ASTE，该任务的目标是从句子中抽取三元组(What,How,Why)，其中What表示aspect，How表示情感极性，Why表示为什么具有这样的情感极性。例如从句子“Waiters are very friendly and the pasta is simply average”中抽取三元组(Waiters, positive, friendly)。

​ 论文针对任务ASTE，提出了一种两阶段框架的解决方案。第一阶段，提取aspect term、opinion term以及判断情感极性。这个阶段会将任务转换为两个序列标注任务，一个序列标注任务用来确定aspect term及其情感极性，另一个序列标注则是用来确定opinion term。第二阶段，将aspect和opinion进行配对。

三、问题的形式化

​ 给定一个长度为$T$的句子 X = { x 1 , … , x T } X=\{x_1,\dots,x_T\} X={x1​,…,xT​}，ASTE的任务是抽取情感三元组。

​ 首先，会将aspect抽取及情感极性判断转换为一个统一的序列标注任务，标注的标签为${\mathcal{Y}}^{\mathcal{T}\mathcal{S}}=${B-POS, I-POS, E-POS, S-POS, B-NEG, I-NEG, E-NEG, S-NEG, B-NEU, I-NEU, E-NEU, S-NEU, O}。句子$X$在这个统一的序列标注任务中会得到预测标签 Y T S = { y 1 T S , … , y T T S } , y i T S ∈ Y T S Y^{\mathcal{TS}}=\{y_1^{\mathcal{TS}},\dots,y_T^{\mathcal{TS}}\},y_i^{\mathcal{TS}}\in\mathcal{Y}^{\mathcal{TS}} YTS={y1TS​,…,yTTS​},yiTS​∈YTS。

​ 其次，opinion抽取也会转换为序列标注任务，标注标签为 Y O P T = { B,I,E,S } ∪ { O } \mathcal{Y}^{\mathcal{OPT}}=\{\text{B,I,E,S}\}\cup\{O\} YOPT={B,I,E,S}∪{O}，对应于句子$X$的预测标签为 Y O P T = { y 1 O P T , … , y T O P T } , y i O P T ∈ Y O P T Y^{\mathcal{OPT}}=\{y_1^{\mathcal{OPT}},\dots,y_T^{\mathcal{OPT}}\},y_i^{\mathcal{OPT}}\in\mathcal{Y}^{\mathcal{OPT}} YOPT={y1OPT​,…,yTOPT​},yiOPT​∈YOPT。

​ 最后，前面2个序列标注任务会得到aspect集合 { T 1 , T 2 , … , T n } \{T_1,T_2,\dots,T_n\} {T1​,T2​,…,Tn​}和opinion集合 { O 1 , O 2 , . . . , O m } \{O_1,O_2,...,O_m\} {O1​,O2​,...,Om​}。然后，两两配对得到aspect-opinion对集合 { ( T 1 , O 1 ) , ( T 1 , O 2 ) , . . . , ( T n , T m ) } \{(T_1,O_1),(T_1,O_2),...,(T_n,T_m)\} {(T1​,O1​),(T1​,O2​),...,(Tn​,Tm​)}，然后从中选出正确的aspect-opinion对。

1. 抽取apsect并判断情感；2. 抽opinion；3. 判断aspect-opinion对

四、模型概览

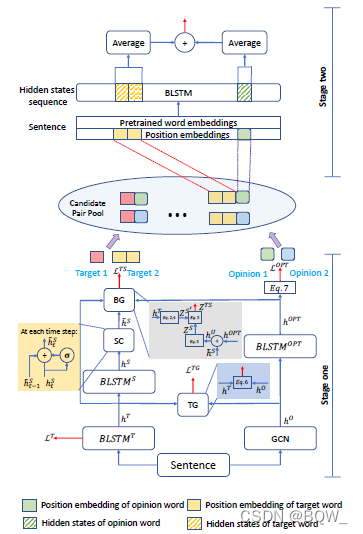
​ 上图是整个模型的结构，其是一个两阶段的框架。第一阶段会预测两种类型的标签，分别是apsect边界和情感极性的统一标签${\mathcal{Y}}^{\mathcal{T}\mathcal{S}}$和opinion边界标签${\mathcal{Y}}^{\mathcal{O}\mathcal{P}\mathcal{T}}$。具体来说，左边的模型包含两个堆叠的BiLSTM，用于预测${\mathcal{Y}}^{\mathcal{T}\mathcal{S}}$。下面的BiLSTM用于执行一个预测apsect的辅助任务，并将产生的辅助信号传递给上面的BiLSTM，上面的BiLSTM用于保证情感的连接性，并最终使用BG组件将所有的信息进行汇合后来预测统一标签。第一阶段右边的模型用于预测opinion的边界，即${\mathcal{Y}}^{\mathcal{O}\mathcal{P}\mathcal{T}}$。整个句子会输入至GCN中，并通过aspect和opinion的依赖关系进行学习。然后，学习到的向量分别被输入至2个不同的模块$\text{TG}$和${\text{BiLSTM}}^{OPT}$，TG模块会结合aspect的边界信息来预测opinion的边界，${\text{BiLSTM}}^{OPT}$则直接预测opinion的边界。

​ 第二阶段会基于第一阶段抽取的aspect和opinion来枚举所有可能的aspect-opinion对，然后基于apsect和opinion的相对距离来产生position embedding，利用BiLSTM编码后能够分别得到apsect和opinion的向量，将两者向量进行拼接后输入二分类器即可。

五、第一阶段

1. aspect抽取和情感极性判断

​ 在上面“问题的形式化”中，将aspect抽取和情感判断转换成了统一标签${\mathcal{Y}}^{\mathcal{T}\mathcal{S}}$并使用序列标注进行解决。论文认为预测aspect的边界有助于预测整个统一标签${\mathcal{Y}}^{\mathcal{T}\mathcal{S}}$，因此会使用一个称为$BiLST{M}^{\mathcal{T}}$的双向LSTM来预测apsect的边界，预测的结果${\mathcal{Y}}^{\mathcal{T}}$为 { B , I , E , S , O } \{B,I,E,S,O\} {B,I,E,S,O}，且模型$BiLST{M}^{\mathcal{T}}$隐藏层的输出表示为$h^{\mathcal{T}}=[{\text{LSTM}}_{\to }^{\mathcal{T}}(x);{\text{LSTM}}_{\leftarrow }^{\mathcal{T}}(x)]$。随后，$h^{\mathcal{T}}$会被输入着一个称为${\text{BiLSTM}}^S$的双向LSTM来预测标签${\mathcal{Y}}^{\mathcal{S}}$，其隐藏层输出为$h^s=[{\text{LSTM}}_{\to }^S(x);{\text{LSTM}}_{\leftarrow }^S(x)]$且${\mathcal{Y}}^{\mathcal{S}}$={B-POS, I-POS, E-POS, S-POS, B-NEG, I-NEG, E-NEG, S-NEG, B-NEU, I-NEU, E-NEU, S-NEU}。（简单总结，第一层BiLSTM预测边界${\mathcal{Y}}^{\mathcal{T}}$，隐藏层输出$h^{\mathcal{T}}$，第二层BiLSTM输入$h^{\mathcal{T}}$来预测${\mathcal{Y}}^{\mathcal{S}}$，隐藏层输出为$h^s$。预测${\mathcal{Y}}^{\mathcal{T}}$是为了让预测${\mathcal{Y}}^{\mathcal{S}}$的边界时更加准确。)

​ 通常一个apsect是由多个token组成的，为了避免预测${\mathcal{Y}}^{\mathcal{S}}$时，多个token的情感不一致。因此，这里会通过gate机制实现一个称为Sentiment Consistency(SC)模块(BiLSTM机制包含三个gate，这里的gate感觉上有点多余)
g t = σ ( W g h t S + b ) h ~ t S = g t ⊙ h t S + ( 1 − g t ) ⊙ h ~ t − 1 S

$$\begin{aligned} &g_t=\sigma(\textbf{W}^gh_t^{S}+\textbf{b})\\ &\tilde{h}_t^S=g_t\odot h_t^S+(1-g_t)\odot\tilde{h}_{t-1}^S \end{aligned}$$ ​gt​=σ(WghtS​+b)h~tS​=gt​⊙htS​+(1−gt​)⊙h~t−1S​​
其中， ${\text{W}}^g$和${\text{b}}^g$是SC模块的模型参数，$\odot$是element-wise乘法，$\sigma$是sigmoid函数。通过该gate可以降低情绪标签剧烈变化的风险。

​ 前面的$BiLST{M}^{\mathcal{T}}$会预测aspect的边界${\mathcal{Y}}^{\mathcal{T}}$并得到$h^{\mathcal{T}}$，若希望基于${\mathcal{Y}}^{\mathcal{T}}$来预测${\mathcal{Y}}^{\mathcal{S}}$，那么${\mathcal{Y}}^{\mathcal{T}}$中的标签会有三种转换情况。举例来说，若$BiLST{M}^{\mathcal{T}}$在某个位置预测的标签是B，那边该标签转换后的结果一定是B-POS、B-NEG、B-NEU中的一个。因此，这里使用一个基于转移矩阵实现的Boundary Guidance(BG)模块。该模块中存在一个可训练的转移矩阵${\text{W}}^{tr}\in {\mathbb{R}}^{|{\mathcal{Y}}^{\mathcal{T}}|\times |{\mathcal{Y}}^{\mathcal{S}}|}$，其中某一个具体取值${\text{W}}_{i,j}^{tr}$表示从标签${\mathcal{Y}}^{{\mathcal{T}}_i}$转移至标签${\mathcal{Y}}^{{\mathcal{S}}_j}$的概率。具体的过程为
z t T = p ( y t T ∣ x t ) = Softmax ( W T h t T ) z t S ′ = ( W t r ) ⊤ z t T

$$\begin{aligned} & z_t^{\mathcal{T}}=\textbf{p}(y_t^{\mathcal{T}}|x_t)=\text{Softmax}(\textbf{W}^\mathcal{T}h_t^{\mathcal{T}})\\ & z_t^{S'}=(\textbf{W}^{tr})^\top z_t^{\mathcal{T}} \end{aligned}$$ ​ztT​=p(ytT​∣xt​)=Softmax(WThtT​)ztS′​=(Wtr)⊤ztT​​
其中，${\text{W}}^{\mathcal{T}}$是可训练参数，$z_t^{S^{\prime }}$是获得的统一标签概率分布。($z_t^{S^{\prime }}$不是最终的统一标签概率，只是其中一部分，之后还会进行一个合并。)

​ $z_t^{S^{\prime }}$在预测统一标签时并没有合并opinion的信息，显然opinion信息对于预测apsect的位置会有很大的帮助。因此这里会将带有opinion信息的向量$h^{\mathcal{O}\mathcal{P}\mathcal{T}}$(后面会介绍怎么得到该向量)和${\tilde{h}}_t^S$进行拼接合并，得到一个更强大的向量$h^{\mathcal{U}}$，然后基于$h^{\mathcal{U}}$在预测一次统一标签的概率分布，
$$z_t^S=\text{p}(y_t^S|x_t)=\text{Softmax}({\text{W}}^S{h}_t^{\mathcal{U}})$$
​ 现在，有两个统计标签的预测概率，分布是$z_t^S$和$z_t^{S^{\prime }}$，现在讨论怎么将两者结合在一起。这里希望学习到一个权重，两者按这个权重进行加权求和。

​ 这里的权重分${\alpha }_t\in \mathbb{R}$的计算是基于称为apsect边界集中度分$c_t$，具体来说
c t = ( z t T ) ⊤ z t T α t = ϵ c t

$$\begin{aligned} c_t=(z_t^{\mathcal{T}})^{\top}z_t^{\mathcal{T}} \\ \alpha_t=\epsilon c_t \end{aligned}$$ ct​=(ztT​)⊤ztT​αt​=ϵct​​
其中，$c_t$是一个0到1的值，其越大表示模型在预测边界时的置信度越高，$ϵ$是一个超参数。

​ 最终预测统一标签的概率分布为
$$z_t^{\mathcal{T}\mathcal{S}}={\alpha }_t{z}_t^{{\mathcal{S}}^{\prime }}+(1-{\alpha }_t)z_t^{\mathcal{S}}$$

2. opinion 抽取

​ 前面介绍了aspect抽取和情感极性判断，这里会介绍opinion抽取的内容。此外，前面在预测$z_t^S$时，使用了$h^{\mathcal{O}\mathcal{P}\mathcal{T}}$，因此本部分也会介绍该向量的由来。

​ 先前的一些研究表明aspect抽取和opinion抽取是互利的，而且直观上也能够判断aspect和opinion是经常共现的。因此，这里希望利用apsect的信息来指导opinion的抽取。具体来说，这里会将句子进行embedding，然后输入至GCN中来学习不同词之间的依赖。GCN的邻接矩阵是基于句子的依赖解析构造的，称为${\text{W}}^{GCN}\in {\mathbb{R}}^{|\mathcal{L}|\times |\mathcal{L}|}$，其中$\mathcal{L}$是句子的长度。例如，第$i$个单词和第$j$个单词具有依赖关系，那么${\text{W}}_{i,j}^{GCN}$和${\text{W}}_{j,i}^{GCN}$均有值1，否则为0。(GCN输出的向量表示为$h^{\mathcal{O}}$)

​ 为了能够利用apsect信息来辅助opinion抽取，这里设计了一个辅助任务来集成aspect的边界信息和GCN的输出，称这部分为Target Guidance(TG)模块。具体来说，就是将apsect边界预测的隐向量$h^{\mathcal{T}}$和GCN输出的向量$h^{\mathcal{O}}$进行拼接，然后用于预测opinion的边界 Y T G = { B , I , E , S } ∪ { O } \mathcal{Y}^{\mathcal{TG}}=\{B,I,E,S\}\cup\{O\} YTG={B,I,E,S}∪{O}，
$$z_t^{\mathcal{T}\mathcal{G}}=\text{p}(y_t^{\mathcal{O}\mathcal{P}\mathcal{T}}|x_t)=\text{Softmax}({\text{W}}^{\mathcal{T}\mathcal{G}}[h_t^{\mathcal{T}};h_t^{\mathcal{O}}])$$
​ 除了将$h^{\mathcal{O}}$与$h^{\mathcal{T}}$合并外，另一部分是将$h^{\mathcal{O}}$送入一个称为$BiLST{M}^{\text{OPT}}$的双向LSMT中，然后输出一个上下文编码向量$h^{OPT}$(前面计算$h^{\mathcal{U}}$会用到)，然后利用其进行opinion边界预测
$$z_t^{\mathcal{O}\mathcal{P}\mathcal{T}}=\text{p}(y_t^{\mathcal{O}\mathcal{P}\mathcal{T}}|x_t)=\text{Softmax}({\text{W}}^{\mathcal{O}\mathcal{P}\mathcal{T}}{h}_t^{\mathcal{O}\mathcal{P}\mathcal{T}})$$

3. 训练

​ 前面的过程会输出$z_t^{\mathcal{T}}$、$z_t^{\mathcal{T}\mathcal{S}}$、$z_t^{\mathcal{T}\mathcal{G}}$和$z_t^{\mathcal{O}\mathcal{P}\mathcal{T}}$，这里使用交叉熵计算损失函数
$${\mathcal{L}}^{\mathcal{I}}=-\frac{1}{T}\sum _{t=1}^T\mathbb{I}(y_t^{\mathcal{I},g})\circ log(z_t^{\mathcal{I}})$$
其中，$\mathcal{I}$是任务指示符和其可能的取值$\mathcal{T},\mathcal{T}\mathcal{S},\mathcal{T}\mathcal{G},\mathcal{O}\mathcal{P}\mathcal{T}$，$\mathbb{I}(y)$表示one-hot编码，$y_t^{\mathcal{I},g}$表示任务$\mathcal{I}$在时间步t处的标签。总的损失函数为所有损失函数之和
$$\mathcal{J}(\theta )={\mathcal{L}}^{\mathcal{T}}+{\mathcal{L}}^{\mathcal{T}\mathcal{S}}+{\mathcal{L}}^{\mathcal{T}\mathcal{G}}+{\mathcal{L}}^{\mathcal{O}\mathcal{P}\mathcal{T}}$$
总结：${\mathcal{L}}^{\mathcal{T}}$用于计算aspect的边界，${\mathcal{L}}^{\mathcal{T}\mathcal{S}}$用于结合opinion信息计算apsect边界和情感极性，${\mathcal{L}}^{\mathcal{T}\mathcal{G}}$用于结合apsect边界信息计算opinion的边界，${\mathcal{L}}^{\mathcal{O}\mathcal{P}\mathcal{T}}$用于直接计算opinion的边界。

​

六、第二阶段

​ 经过第一阶段后，每个句子都会输出两个标签集合，分别是apsect和opinion，记为 { T 1 , T 2 , … , T n } \{T_1,T_2,\dots,T_n\} {T1​,T2​,…,Tn​}和 { O 1 , O 2 , … , O m } \{O_1,O_2,\dots,O_m\} {O1​,O2​,…,Om​}，其中$n$和$m$表示数量。枚举所有可能的aspect-opinion对来生成候选对池 { ( T 1 , O 1 ) , ( T 2 , O 2 ) , … , ( T n , O m ) } \{(T_1,O_1),(T_2,O_2),\dots,(T_n,O_m)\} {(T1​,O1​),(T2​,O2​),…,(Tn​,Om​)}，接下来就是判断每个aspect-opinion对是否有效。

1. 位置嵌入(position embedding)

​ 为了能够利用aspect和opinion的位置关系，这里会计算aspect中心词至opinion中心词之间单词的数量，用于表示两者的距离。为了便于训练，将aspect和opinion间的距离当做其位置索引，从而创建出position embedding(位置嵌入)。索引为0表示该单词既不是apsect，也不是opinion。可以观察下表中的$(Waiter,friendly)$和$(fugusashimi,friendly)$的位置索引。

2. 成对编码与分类

​ 这里将Glove词向量和position embedding进行拼接，然后输入至BiLSTM层来编码aspect和opinion上下文信息。将aspect和opinion位置输出的词向量进行各自平均，并将得到的2个向量进行拼接。最后将拼接后的向量送至softmax层进行分类。

​ 训练时使用标注好的aspect-opinion对，测试时直接使用模型在候选对池上进行预测。