数学遇上人工智能，深度学习架构迎来最强挑战者 KAN，MLP 的时代结束了？_kan机器学习

文 | 王启隆

出品｜《新程序员》编辑部

多层感知器（MLP, Multilayer Perceptron）作为人工神经网络的一个基本架构，一直在历史上扮演着至关重要的角色。MLP 可以被视为深度学习领域的“基石”或“基础构件”，它的意义在于：

1. 基础模型：MLP 作为最早被广泛研究和应用的神经网络模型之一，是许多复杂深度学习架构的起点和基础。它奠定了神经网络能够解决非线性问题的基础，是理解更高级神经网络结构的入门。

2. 功能强大：虽然结构相对简单，但 MLP 已经能够处理复杂的分类和回归任务，展示了神经网络的强大适应能力和学习能力，为后续深度学习的发展铺平了道路。

3. 理论与实践结合：MLP 不仅在理论上证明了神经网络的普遍近似能力，而且在实践中也取得了显著的性能表现，特别是在早期的手写数字识别等机器学习应用当中。

但 AI 发展到今天，MLP 几乎一点没变，人类的需求却越来越多了。MLP 在庞大的需求压力下暴露出了一个又一个缺点：可解释性和交互性不足、处理大尺寸图像的时候计算复杂且有过拟合问题、缺乏灵活性和适应性、自动特征提取方面的能力较弱……

4 月 30 日，全新的神经网络架构 KAN 横空出世。它的使命只有一个：取代 MLP。

KAN 全称 Kolmogorov-Arnold Networks，其最大意义就是作为 MLPs 最具潜力的替代品，提出了全新的架构思路。KAN 受到 Kolmogorov-Arnold 表示定理的启发，在以下几个方面展现了显著的优势：

1. 增强的准确性与效率：与传统 MLPs 相比，KANs 能够使用更少的参数达到相同或更好的准确度，尤其是在数据拟合和偏微分方程求解等任务中。这意味着在处理复杂科学和数学问题时，KANs 可能提供更高效的解决方案。

2. 可学习的激活函数：KANs 的一个核心创新点是将可学习的激活函数置于边（权重）上，而非节点（如 MLPs）。这不仅允许模型学习到更复杂的函数关系，还使得每个权重参数由一个参数化的样条函数代替，从而提高了模型的表达能力。

3. 增强的可解释性：KANs 的结构可以直观地被可视化，并且容易与人类用户交互，这有助于科学家们理解模型内部的工作原理，甚至直接参与到模型的优化和“发现”过程中。通过手动调整和简化 KANs，科学家们能够引导模型发现或验证数学与物理定律，促进 AI 与科学家之间的合作。

4. 适应性和灵活性：利用样条基函数的内在局部性，KANs 支持适应性设计和训练，比如引入多级训练策略，提高模型的准确性和训练效率。这种适应性使得 KANs 能更好地匹配不同任务的需求。

5. 自动发现高效结构：实验结果显示，自动发现的 KAN 结构通常比人为构建的更为紧凑，表明 Kolmogorov-Arnold 表示可能在某些情况下能以比预期更高效的方式压缩和表示信息，尽管这也可能给模型的直接可解释性带来挑战。

此前，在 CSDN 新程序员对图灵奖得主 Joseph Sifakis 的采访中，这位老教授曾感叹符号主义的落寞，并对符号主义 AI 的理性特征大表赞赏。如今数学重新遇上了人工智能，脱胎换骨的符号人工智能或将以 KAN 的身份重新归来。

看到这里，你可能已经发现了：KAN 的数学解释能力相当超群，且它最终要解决的，很可能就是曾经被视为“蹭热点”“伪命题”“不可能”的 AI4Science。依靠 KAN 在科学相关任务的能力，让人工智能，助力未来的科研与自然规律发现。

论文链接：https://arxiv.org/html/2404.19756v1（HTML 版本）https://arxiv.org/pdf/2404.19756v1（PDF 版本）

GitHub 链接：https://github.com/KindXiaoming/pykan

66 年前的定理

KAN 的灵感来源：Kolmogorov-Arnold 表示定理是个啥？

Kolmogorov-Arnold 表示定理（Kolmogorov-Arnol'd Representation Theorem 或 Kolmogorov Superposition Theorem）是数学中的一个重要结果，由苏联数学家安德烈·尼古拉耶维奇·科尔莫戈罗夫（Andrey Nikolaevich Kolmogorov）和弗拉基米尔·伊戈列维奇·阿诺尔德（Vladimir Igorevich Arnold）分别独立提出。这个定理表明了连续函数的一种非常有趣的表示形式，它对于理解函数的复杂性以及在某些领域，如机器学习、科学计算和函数逼近有着重要的意义。

Kolmogorov-Arnold 定理大致上是说，任何在 n 维实数空间上的连续函数 f(x)，其中 x = (x1, x2, ..., xn)，都可以表示为一个单一变量的连续函数 h 和一系列连续的双变量函数 gi 和 gi,j 的组合。具体来说，定理表明存在这样的表示形式：

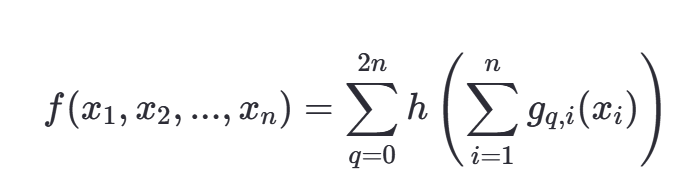
其中，h 是一个在实数轴上的连续函数，而每个 gi 和 gi,j 都是定义在实数上的连续双变量函数。这个表示表明，即使在一个高维空间中的复杂函数，也可以通过一系列较低维度的函数操作来重构。

1957 年，“现代概率论之父”科尔莫戈罗夫（下图左）首次提出了这个定理，展示了一种将多变量函数简化为单变量函数叠加的方法，这一成果在当时是极为创新的。后来，阿诺尔德（下图右）对科尔莫戈罗夫的工作进行了独立的证明和拓展，使得这个定理得到了更广泛的注意和应用。

无巧不成书，在 Kolmogorov-Arnold 表示定理诞生一年之后的 1958 年，被后世称为“神经网络之父”的弗兰克·罗森布拉特（Frank Rosenblatt）在他的著作《Perceptron》中介绍了一个包含输入层、隐藏层（该隐藏层具有随机且不进行学习的权重）以及具有学习连接的输出层的分层网络，如今这被视为 MLP 的雏形，它并不等同于现代意义上具有反向传播能力的 MLP，也未形成深度学习网络的概念。

KAN 的设计灵感正是来源于 Kolmogorov-Arnold 表示定理。前面提到，该定理表明，任何多元连续函数都可以表示为单变量连续函数的两层嵌套叠加。基于这一理论，研究人员创新性地将此数学概念应用到了神经网络架构的设计中，创造出了 KAN。

当然，KAN 的名字 Kolmogorov-Arnold Network 也正是直接以这两位数学家命名，未来 KAN 若是成为了机器学习的范式，全世界都需要记住这两位的名字……

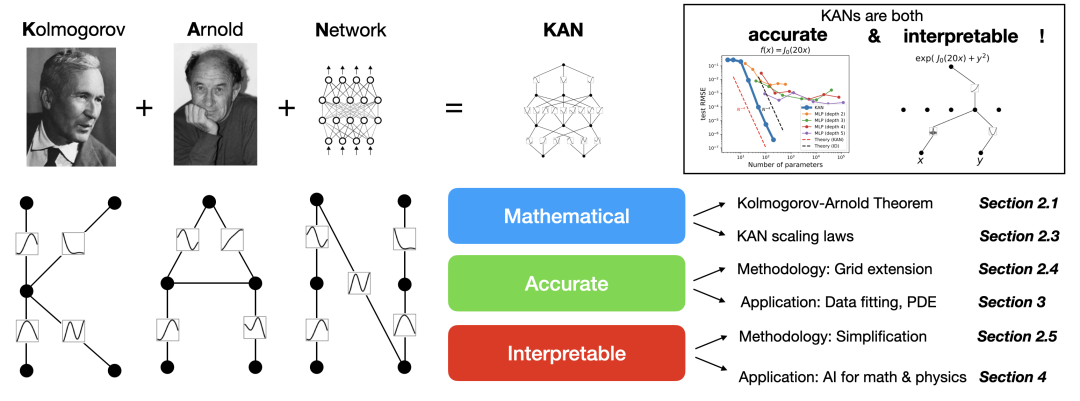
KAN 的核心创新在于，它不是像传统 MLP 那样在网络的神经元上应用固定的激活函数，而是在权重上应用可学习的激活函数。这些一维激活函数被参数化为样条曲线，从而使得网络能够以一种更灵活、更接近 Kolmogorov-Arnold 表示定理的方式来处理和学习输入数据的复杂关系。这种设计使得 KAN 能够以一种理论上更高效、更通用的方式逼近复杂的函数关系，理论上可能在某些任务上超越了 MLP 的性能。

简而言之，KAN 是 Kolmogorov-Arnold 表示定理的一次直接应用，它试图通过参数化的激活函数和特殊的网络架构设计，实现对复杂数据分布更优的建模能力，从而在实践中展现出相较于传统 MLP 架构的优越性。

Yes we KAN！

KAN 的论文一作刘子鸣（下图左）是一位兼具物理与机器学习背景的研究者，他出生于武汉，在北京大学物理学系完成本科学业，早年还在微软亚洲研究院实习。如今刘子鸣正于麻省理工（MIT）与人工智能与基础科学研究所（IAIFI）攻读博士三年级，师从 Max Tegmark（下图右）。KAN 的成果正是由刘子鸣与老师 Max Tegmark 及来自 MIT、东北大学、IAIFI 和加州理工学院（Caltech）的优秀合作者共同完成。

刘子鸣的研究热情聚焦于 AI 与物理学（乃至整个科学界）的交融地带，探索三个核心方向：

• AI 背后的物理学（Physics of AI）。从物理学原理洞悉 AI 本质：“简约如物理的 AI”；

• 物理学启迪的 AI（Physics for AI）。借鉴物理规律创新 AI 技术：“自然流畅如物理的 AI”；

• 助力物理学的 AI（AI for physics）。以 AI 强化物理学研究：“能力比肩物理学家的 AI”。

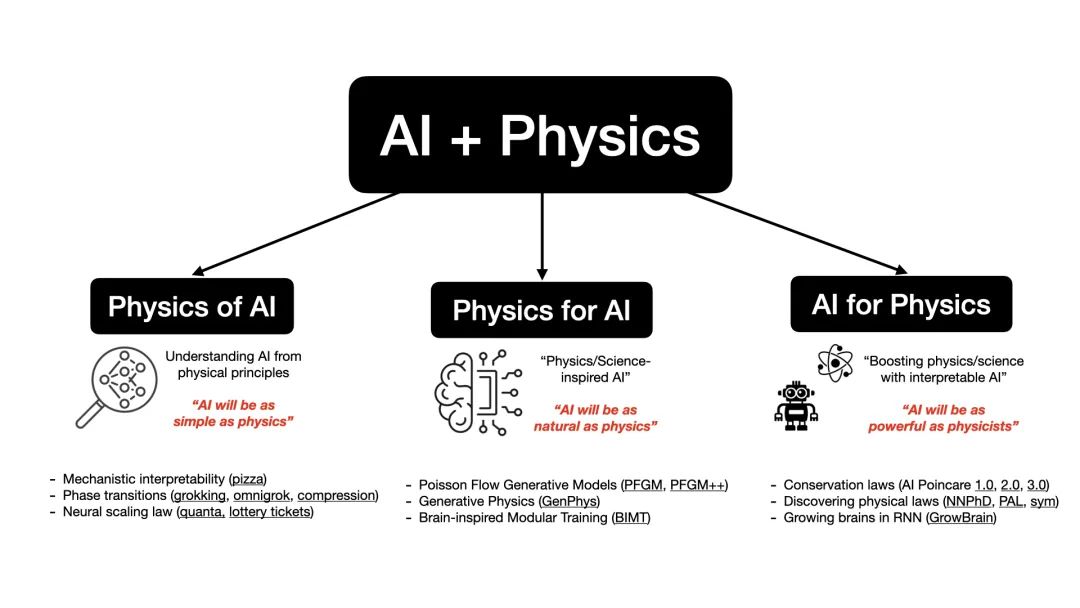
以此愿景为核心，他致力于运用 AI+物理学打造更加美好的世界，涉猎领域广泛，涵盖物理定律发掘、物理启发的生成模型、机器学习理论及模型可解释性等诸多方面。

在 X 上，刘子鸣也是进一步分享了许多技术细节：

• 多层感知器（MLPs）的设计理念受到了万能近似定理（UAT）的启发。这个定理表明，在理想条件下，具有足够多隐藏层的 MLP 能够以任意精度逼近任何连续函数。然而，它并没有直接说明固定宽度（即网络的层数和每层的神经元数量保持不变）的网络能否达到无限的预测精度。而基于 Kolmogorov-Arnold 表示定理的 KANs，则在满足一定条件的情况下，理论上能够实现固定宽度网络对某些函数的无限精度逼近（事实上也伴随着特定的限制或前提条件）。

• 传统上，MLPs 在网络中的神经元位置应用激活函数。而 KANs 则可以打破常规，将（可学习的）激活函数直接置于权重上。

• 神经网络的“scaling laws”：KANs 相比 MLPs 展现出更快的规模增长速度，这一优势在数学上得益于 Kolmogorov-Arnold 表示定理的坚实基础。所以 KANs 的规模增长指数不仅在理论上成立，实际上也可通过实验观察到，证实了其在实践中同样高效的扩展能力。

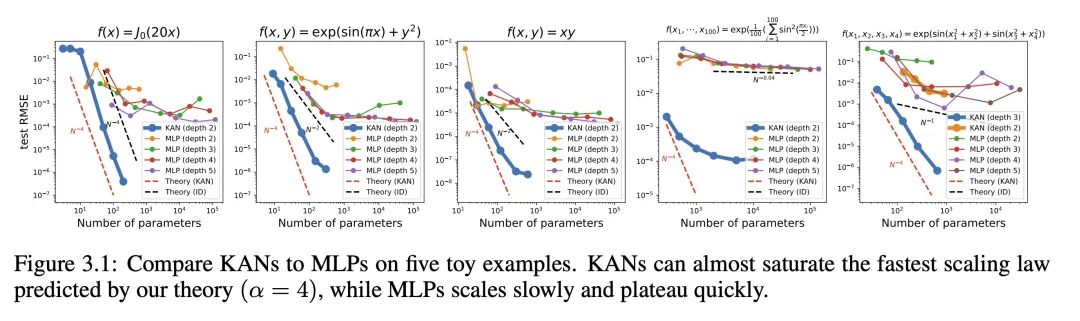
• KANs 在函数拟合任务中表现出更高的准确性，例如对于特定函数的拟合，它们的性能超越了传统的 MLPs。

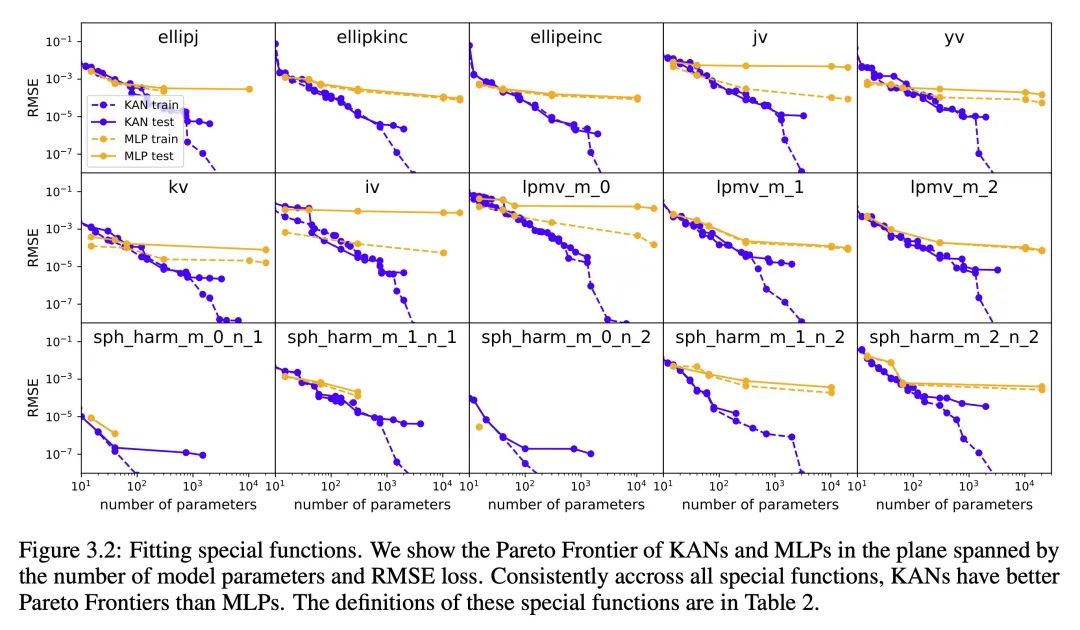
• 在求解偏微分方程（如泊松方程）的问题上，KANs 相较于 MLPs 展现了更高的求解精度。

……

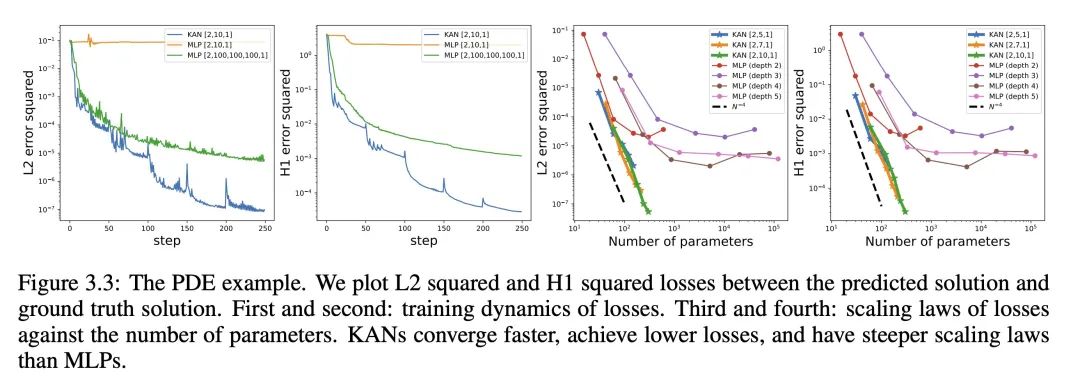
MLPs 不行，KANs 行——千言万语束成一句话：Yes we KAN！

再让我们进一步阅读论文，看看还有哪些奥秘：

架构设计

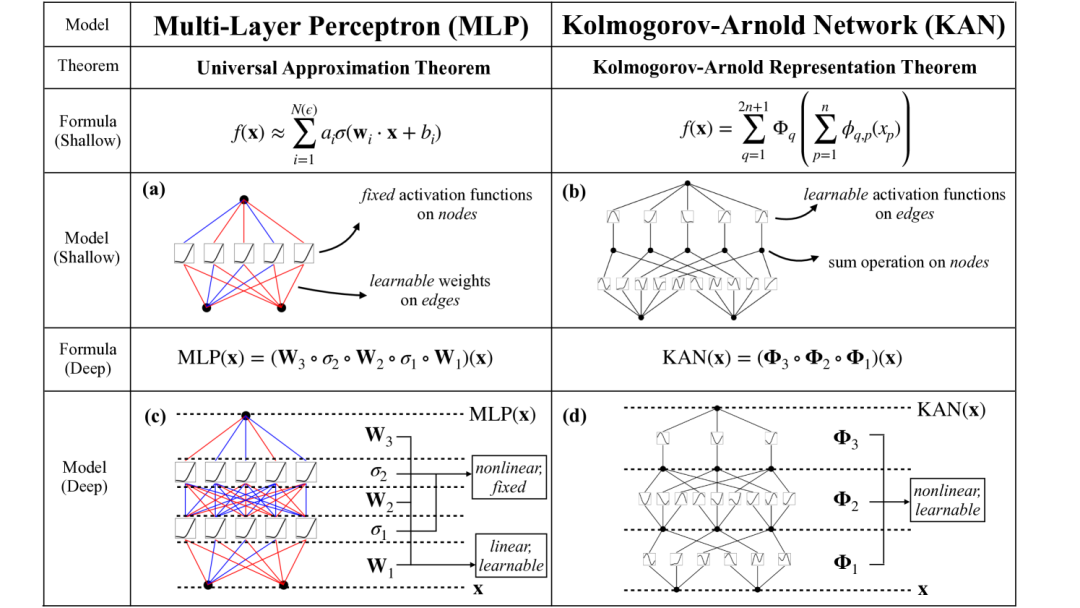
KANs 的核心创新在于它们将传统的 MLPs 中的节点激活函数转移到了网络的边（权重）上。论文中提到，“KANs 在边上具有可学习的激活函数，而 MLPs 则在节点上设置固定激活函数。”

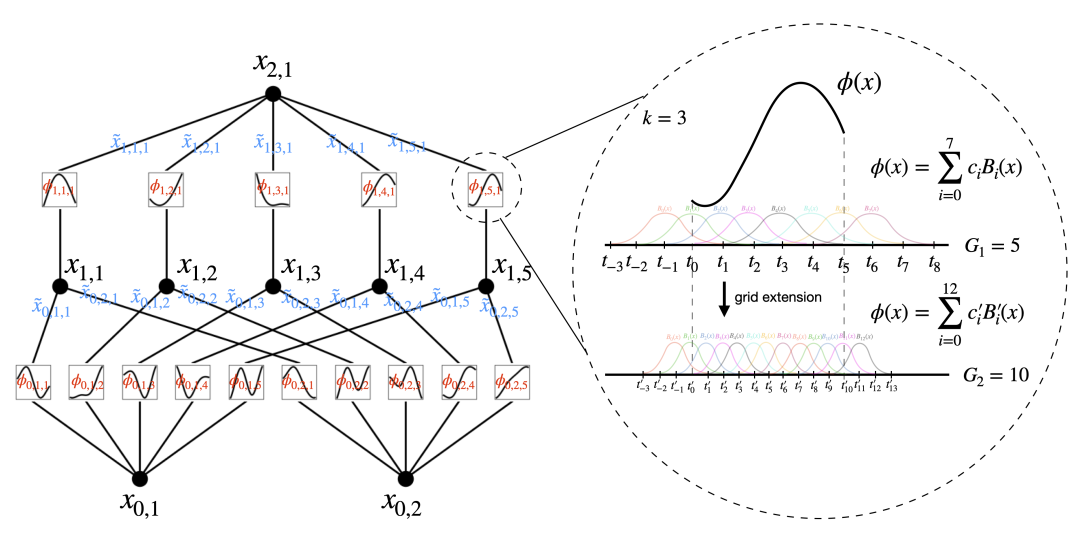
具体实现上，KAN 的所有权重参数被单变量函数取代，这些函数被参数化为B样条曲线，每个一维函数都具有可训练的局部 B 样条基函数系数（参见下图右）。这种设计允许网络更灵活地逼近复杂的函数关系。

克服传统限制

论文指出，尽管原始的 Kolmogorov-Arnold 表示仅对应于两层网络，但作者们通过类比 MLPs 的层次结构，提出了一种深化 KAN 的方法。他们定义了一个 KAN 层，它由一组一维函数构成，这些函数以矩阵形式组织，输入和输出维度分别为 nin 和 nout。

文中阐述：“一个具有 nin 维输入和 nout 维输出的 KAN 层可以定义为 1D 函数的矩阵 Φ={ϕq,p}，其中函数 ϕq,p 具有可训练参数。” 这一突破使得 KAN 能够通过堆叠更多这样的层来构建更深层的网络，从而理论上能够更加精确地逼近任意复杂度的函数。

使用网格扩展（Grid Extension）以提升精度

KANs 的一个关键优势在于它们能够利用样条函数的特性，通过增加网格的精细度（即网格扩展），理论上可以无限接近目标函数的精度。与 MLPs 不同，后者提高精度主要依赖于增加网络的宽度和深度，这通常伴随着训练成本的大幅增加且效果提升缓慢，KANs 则可以通过简单地细化其内部样条函数的网格来实现，无需从头开始重新训练更大的模型。

作者通过一个示例（包含变量 x 和 y 的复合函数）来展示网格扩展的效果，说明随着网格点数量的增加，训练损失迅速下降，但测试损失呈现先降后升的 U 形曲线，反映了偏差-方差权衡的问题。这一观察结果提示，存在一个最优的网格大小，即插值阈值，使得模型既不过拟合也不欠拟合，达到最佳泛化性能。

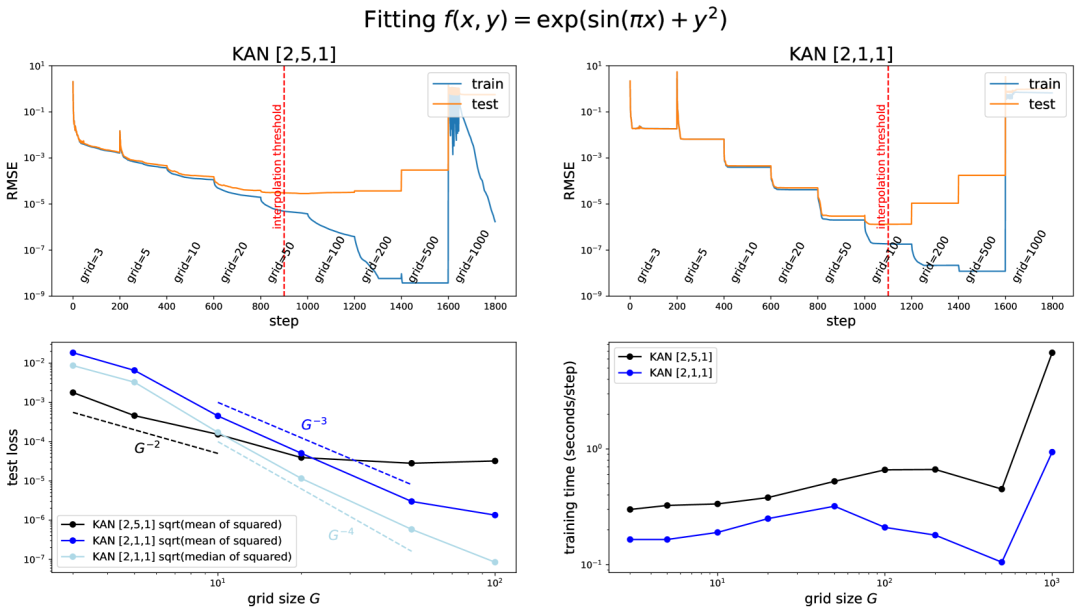
研究发现，较小规模的 KANs（例如上图 [2,1,1] 配置）相比较大规模的（如上图 [2,5,1] 配置）在特定情况下能取得更好的测试性能，这突显了选择合适 KAN 架构的重要性。此外，KANs 还引入了外部自由度（节点连接构成的计算图）与内部自由度（激活函数内的网格点）的概念。前者负责学习多变量的组合结构，而后者专注于学习单变量函数，这两种自由度的结合使 KANs 具有独特的优势。

应用实例

在数学和物理学的应用上，论文提到了 KANs 能够辅助科学家发现或重新发现定律。例如，在无监督模式下，KANs 成功地重新发现了已知的数学关系，如体积 V 与密度 μr 及长度 λ 的关系 V=μrλ。此外，KANs 还探索了安德森局域化现象，这是一种量子系统中的重要现象，其中随机无序导致电子波函数局限，进而阻止所有传输。论文提及：“在三维中，存在一个临界能量，它划分了扩展态与局域态，称为移动边缘。对这些移动边缘的理解对于解释固体中的金属-绝缘体转变等基本现象至关重要。”

未来是用 MLP 还是 KAN？

刘子鸣在 X 上回答了这个问题，并给出了理由：

根据我们的实证研究结果，我们相信 KANs 凭借其高准确性、参数效率及可解释性，将成为 AI 与科学结合领域中一个极为有用的模型或工具。至于 KANs 在机器学习相关任务上的应用潜力，目前更多处于推测阶段，这将是未来研究的课题。

事实上，论文中也探讨了这个问题。当前，KANs 面临的主要瓶颈在于其训练速度较慢。在相同参数数量下，KANs 的训练速度通常比 MLPs 慢大约 10 倍。研究团队在优化 KANs 的效率方面尚未进行深度探索，因此他们认为 KANs 训练速度慢更多是一个有待未来工程技术改进的问题，而非根本性局限。

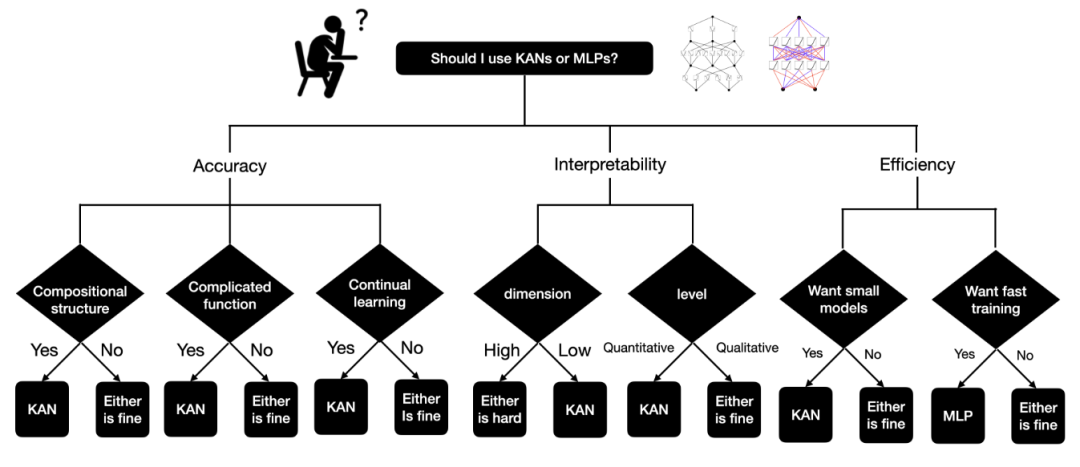
如果追求快速训练模型，MLPs 无疑是首选。但在其他情形下，尤其是在乎模型的可解释性和/或预测准确性，且不把训练速度视为首要考量因素时，KANs 应是可媲美甚至优于MLPs的选择，值得尝试。

下图的决策树有助于判断何时采用 KAN。简而言之，如果你重视模型的可解释性和/或追求高精度，且不介意较慢的训练速度，作者推荐尝试使用 KANs。