- 1Macs Fan Control Pro for Mac:全面优化Mac风扇控制软件
- 2Hadoop高可靠集群搭建步骤(手把手教学)【超级详细】_hadoop系统搭建
- 3完美解决:ERROR 1064 (42000): You have an error in your SQL syntax; check the manual that corresponds to
- 4pytorch学习笔记(三)用nn.cross_entropy所遇到的问题_nn.cross_entropy axis
- 5中国AIGC数据标注全景报告:百亿市场规模,百万就业缺口
- 6HTML最新面试题(笔试面试题)_html 笔试|面试
- 7为什么我不建议普通人学Python?_为什么不建议学python
- 8PotatoPie 4.0 实验教程(21) —— FPGA实现摄像头图像二值化(RGB2Gray2Bin)
- 9【idea】tag(git标签)的使用_idea查看tag
- 10华为先进芯片麒麟9010效能再升级,挑战新高度 | 百能云芯_华为9010芯片最新官方消息
基于Frank Wolfe算法,求解交通分配UE模型(Python & NetWorkX)_beckmann 提出的ue状态下的优化模型
赞
踩
目录
一、用户均衡模型简略介绍
1.1 Wardrop第一原理
- 道路的利用者,都确切知道网络的交通状态,并试图选择最短路径
- 当网络达到平衡状态时,每个OD对的各条被使用的路径,行驶时间相等,且行驶时间最短
- 没有被使用的路径的行驶时间大于或等于最小行驶时间
1.2 用户均衡模型
满足Wardrop第一原理的交通分配模型,称为用户均衡模型。
1956年Beckmann提出了一种满足Wardrop第一原理的数学规划模型。模型核心是,交通网络中的用户,都试图选择最短路径,而最终使得被选择的路径的阻抗最小且相等。该数学规划模型为:
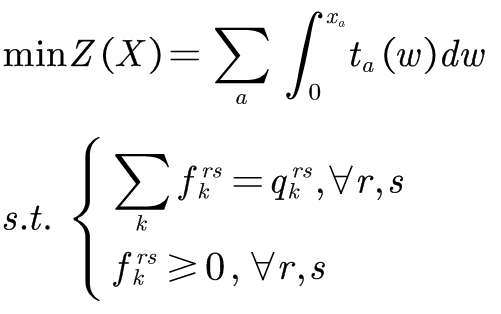
1.3 BPR函数
在用户均衡模型中,为路阻函数,我们一般采用BPR函数,即:
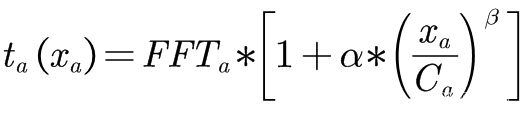
,表示最快通过路段a的时间;
- α常取0.15,β常取4.0 ;
,表示路段a的通行能力;
,表示路段a的流量
1.4 用户均衡模型的积分项
为便于后续求解,我们将BPR函数代入,进行积分计算,过程如下:
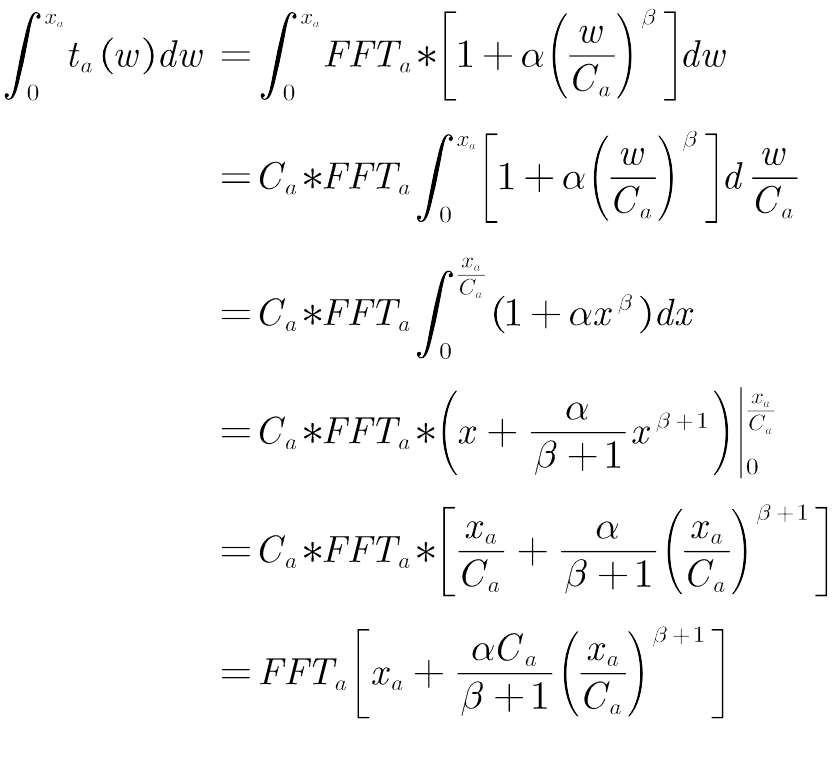
因此,我们的目标函数为:
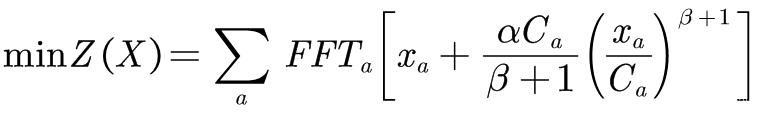
当然,系统最优模型,是与用户均衡模型相通的。对于系统最优模型,其目标函数表达式为

二、Frank Wolfe算法求解步骤
友情提醒:后面若对代码主体逻辑有疑惑,返回看看这部分。
步骤1:初始化。基于零流图的路阻,依次搜索每一个OD对 r,s 所对应的最短路径,并将 r,s 间的OD流量,全部分配到对应的最短路径上,得到初始路段流量,并令迭代次数n=1。
步骤2:更新路阻。根据BPR函数,分别代入每个路段的初始流量,求得阻抗
步骤3:下降方向。基于阻抗,按照步骤1中的方法(最短路全有全无分配),将流量重新分配到对应路径上,得到临时路段流量
,进而得到
步骤4:搜索最优步长,并更新流量。采用二分法,搜索最优步长,并令
。其中,最优步长满足:
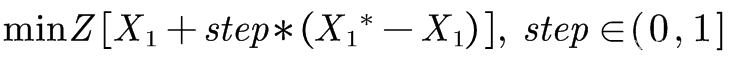
步骤5:结束条件。如果,则算法结束;否则n=n+1,转至步骤2。此处的e 表示误差阈值,在代码部分用max_err表示。
三、代码
代码基于Python的NetWorkX库编写,这样将大大减少我们代码编写的工作量,并且更易于阅读。我们以SiouxFalls交通网络为例,进行交通网络构建与流量分配。
3.1 导入必要的库
- import pandas as pd
- import numpy as np
- import networkx as nx
- import matplotlib.pyplot as plt
- from scipy.optimize import minimize_scalar
- pandas,用于读取文件;
- numpy在计算误差时使用;
- networkx贯穿整个代码;
- matplotlib用于绘制交通网络图
- scipy在搜索最优步长时用到。
3.2 构建交通网络
- def build_network(Link_path, Node_path):
- # 读取点数据、边数据
- links_df = pd.read_csv(Link_path)
- # 需要注意使用from_pandas_edge,其读取的边的顺序和csv中边的顺序有差异
- G = nx.from_pandas_edgelist(links_df, source='O', target='D', edge_attr=['FFT', 'Capacity'], create_using=nx.DiGraph())
- nx.set_edge_attributes(G, 0, 'flow_temp')
- nx.set_edge_attributes(G, 0, 'flow_real')
- nx.set_edge_attributes(G, 0, 'descent')
- nx.set_edge_attributes(G, nx.get_edge_attributes(G, "FFT"), 'weight')
-
- # 获取节点位置信息
- nodes_df = pd.read_csv(Node_path)
- node_positions = {}
- for index, row in nodes_df.iterrows():
- node_positions[row['id']] = (row['pos_x'], row['pos_y'])
- # 更新图中节点的位置属性
- nx.set_node_attributes(G, node_positions, 'pos')
- return G

- Link_path,表示路网文件路径。下载链接见文末,数据示例如下:
| O | D | FFT | Capacity |
| 1 | 2 | 6 | 25900.20064 |
| 1 | 3 | 4 | 23403.47319 |
| 2 | 1 | 6 | 25900.20064 |
| 2 | 6 | 5 | 4958.180928 |
| 3 | 1 | 4 | 23403.47319 |
- Node_path,表示节点文件路径。下载链接见文末,数据示例如下:
| id | pos_x | pos_y |
| 1 | 2 | 2 |
| 2 | 13 | 2 |
| 3 | 2 | 5 |
| 4 | 5 | 5 |
| 5 | 9 | 5 |
- flow_real,表示每次迭代更新后的路段流量或初始化流量,所有路段的flow_real组成
- flow_temp, 所有路段的flow_temp组成
- descent,表示flow_temp与flow_real的差值,所有路段的descent组成
- weight,表示路阻。初始的路阻,由于路段流量都是0,所以直接用FFT。后续将用BPR函数计算
3.3 绘制交通路网图
- def draw_network(G):
- pos = nx.get_node_attributes(G, "pos")
- nx.draw(G, pos, with_labels=True, node_size=200, node_color='lightblue', font_size=10, font_weight='bold')
- plt.show()
构建交通网络后,我们来看一看这个SiouxFalls网络长什么样子吧
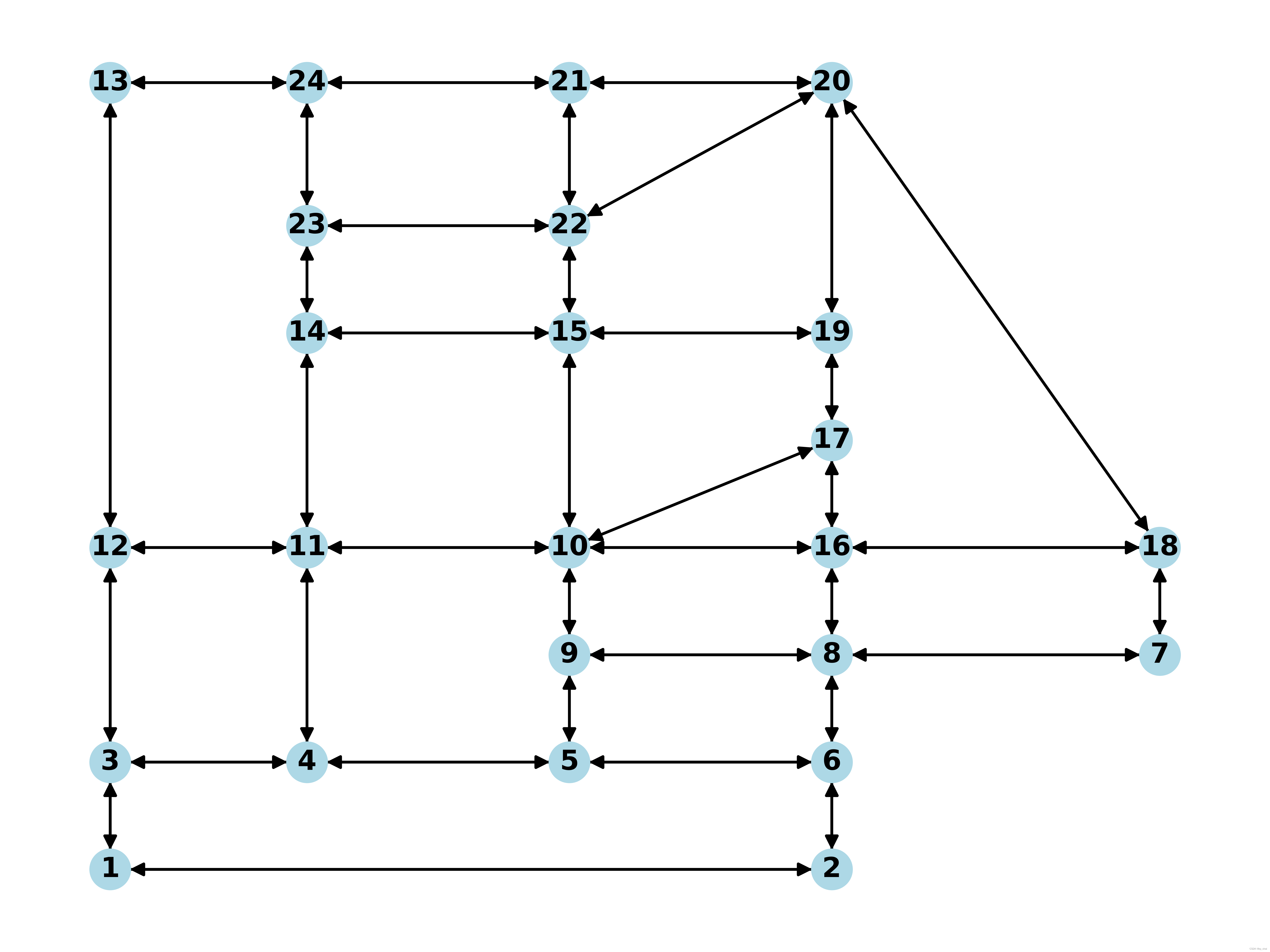
3.4 定义BPR函数
- def BPR(FFT, flow, capacity, alpha=0.15, beta=4.0):
- return FFT * (1 + alpha * (flow / capacity) ** beta)
- FTT,表示最快通过时间;
- flow,表示路段流量;
- capacity,表示路段通行能力;
- alpha和beta,是BPR函数的参数,在此取默认值。
3.5 初始化路网流量
- def all_none_initialize(G, od_df):
- # 这个函数仅使用一次,用于初始化
- # 在零流图上,按最短路全有全无分配,用于更新flow_real
- for _, od_data in od_df.iterrows():
- source = od_data["o"]
- target = od_data["d"]
- demand = od_data["demand"]
- # 计算最短路径
- shortest_path = nx.shortest_path(G, source=source, target=target, weight="weight")
- # 更新路径上的流量
- for i in range(len(shortest_path) - 1):
- u = shortest_path[i]
- v = shortest_path[i + 1]
- G[u][v]['flow_real'] += demand
- # 初始化流量后,更新阻抗
- for _, _, data in G.edges(data=True):
- data['weight'] = BPR(data['FFT'], data['flow_real'], data['Capacity'])

这个函数仅使用一次,用于初始化。在零流图上,按最短路全有全无分配,用于得到。
- od_df表示pd.Dataframe数据格式的OD流量信息。ODParis.csv示例数据如下:
| o | d | demand |
| 1 | 2 | 100 |
| 1 | 3 | 100 |
| 1 | 4 | 500 |
| 1 | 5 | 200 |
| 1 | 6 | 300 |
| 1 | 7 | 500 |
3.6 获取 flow_temp
flow_temp,即
- def all_none_temp(G, od_df):
- # 这个是虚拟分配,用于得到flow_temp
- # 每次按最短路分配前,需要先将flow_temp归零
- nx.set_edge_attributes(G, 0, 'flow_temp')
- for _, od_data in od_df.iterrows():
- # 每次更新都得读OD,后面尝试优化这个
- source = od_data["o"]
- target = od_data["d"]
- demand = od_data["demand"]
- # 计算最短路径
- shortest_path = nx.shortest_path(G, source=source, target=target, weight="weight")
- # 更新路径上的流量
- for i in range(len(shortest_path) - 1):
- u = shortest_path[i]
- v = shortest_path[i + 1]
- # 更新流量
- G[u][v]['flow_temp'] += demand

3.7 获取下降方向descent
descent,即
- def get_descent(G):
- for _, _, data in G.edges(data=True):
- data['descent'] = data['flow_temp'] - data['flow_real']
3.8 定义目标函数
- def objective_function(temp_step, G):
- s, alpha, beta = 0, 0.15, 4.0
- for _, _, data in G.edges(data=True):
- x = data['flow_real'] + temp_step * data['descent']
- s += data["FFT"] * (x + alpha * data["Capacity"] / (beta + 1) * (x / data["Capacity"]) ** (beta + 1))
- return s
该部分代码,对应本文1.4部分的目标函数,即:
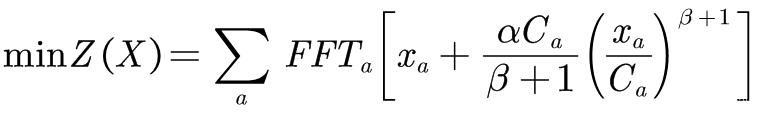
如果需要求解系统最优模型,则目标函数为
 代码则需替换为:
代码则需替换为:
- def objective_function(temp_step, G):
- s, alpha, beta = 0, 0.15, 4.0
- for _, _, data in G.edges(data=True):
- x = data['flow_real'] + temp_step * data['descent']
- s += x * BPR(data["FFT"], x, data["Capacity"])
- return s
3.9 一维搜索最优步长,并更新流量
- def update_flow_real(G):
- # 这个函数用于调整流量,即flow_real,并更新weight
- best_step = get_best_step(G) # 获取最优步长
- for _, _, data in G.edges(data=True):
- # 调整流量,更新路阻
- data['flow_real'] += best_step * data["descent"]
- data['weight'] = BPR(data['FFT'], data['flow_real'], data['Capacity'])
-
-
- def get_best_step(G, tolerance=1e-4):
- result = minimize_scalar(objective_function, args=(G,), bounds=(0, 1), method='bounded', tol=tolerance)
- return result.x
3.10 主函数
- def main():
- G = build_network("Link.csv", "Node.csv") # 构建路网
- draw_network(G) # 绘制交通路网图
- od_df = pd.read_csv("ODPairs.csv") # 获取OD需求情况
- all_none_initialize(G, od_df) # 初始化路网流量
- print("初始化流量", list(nx.get_edge_attributes(G, 'flow_real').values()))
-
- epoch = 0 # 记录迭代次数
- err, max_err = 1, 1e-4 # 分别代表初始值、最大容许误差
- f_list_old = np.array(list(nx.get_edge_attributes(G, 'flow_real').values()))
- while err > max_err:
- epoch += 1
- all_none_temp(G, od_df) # 全有全无分配,得到flow_temp
- get_descent(G) # 计算梯度,即flow_temp-flow_real
- update_flow_real(G) # 先是一维搜索获取最优步长,再调整流量,更新路阻
-
- # 计算并更新误差err
- f_list_new = np.array(list(nx.get_edge_attributes(G, 'flow_real').values())) # 这个变量是新的路网流量列表
- d = np.sum((f_list_new - f_list_old) ** 2)
- err = np.sqrt(d) / np.sum(f_list_old)
- f_list_old = f_list_new
-
- print("均衡流量", list(nx.get_edge_attributes(G, 'flow_real').values()))
- print("迭代次数", epoch)
- # 导出网络均衡流量
- df = nx.to_pandas_edgelist(G)
- df = df[["source", "target", "flow_real"]].sort_values(by=["source", "target"])
- df.to_csv("网络均衡结果.csv", index=False)
-
-
- if __name__ == '__main__':
- main()

- epoch,表示迭代次数
- err,表示误差初始值
- max_err,表示最大容许误差
- f_list_new, f_list_old分别表示
和
,用于计算误差
四、所用文件
下载链接:交通分配


