2024山东省大学生数学建模C题校园的快速疏散与转运预案代码论文思路分析_山东省数学建模2024c

2024山东省大学生数学建模C题33页论文和代码已完成，代码为C题全部问题的代码，论文包括摘要、问题重述、问题分析、模型假设、符号说明、模型的建立和求解（问题1模型的建立和求解、问题2模型的建立和求解、问题3模型的建立和求解、问题4模型的建立和求解）、模型的评价等等

2024山东省大学生数学建模C题论文和代码获取↓↓↓↓↓
https://www.yuque.com/u42168770/qv6z0d/az93tb4gs2v4u86g

摘要

本文针对校园应急管理中的快速疏散和转运问题,建立了一系列优化模型并进行了详细求解。通过对问题的分析和建模,提出了切实可行的应急预案,为校园突发事件的应对提供了有力的理论支持。

首先,针对问题1中的快速疏散策略优化,我们建立了一个基于最短距离原则的疏散路径优化模型。该模型考虑了校区内宿舍楼数量、集结点位置和容纳能力等实际因素,以最小化总疏散时间为目标。我们采用了Dijkstra算法和贪心分配的方法进行求解。结果显示,对于本次模拟数据,总疏散时间约为62.29秒,各集结点的负载分配较为均衡。该模型的创新点在于采用基于距离最短的优化目标,能够给出一个高效的疏散策略,同时考虑了集结点的容量约束,能够更好地反映实际情况。

针对问题2中的分批疏散优化,我们建立了一个分批安排疏散的优化模型。该模型在问题1的基础上,进一步考虑了集结点容量限制的问题,通过将疏散过程划分为多批次进行。我们设计了一个基于贪心分配和批次优化的算法进行求解,最终找到了使总疏散时间最短的分批疏散方案。该方案能够较好地平衡各批次的疏散时间,提高了整体疏散效率。该模型的创新点在于将疏散过程划分为多批次,有效缓解了单次疏散时的拥挤问题,同时提出了一种基于贪心分配和批次优化的求解方法。

针对问题3中的车辆转运优化,我们建立了一个以最小化总转运成本为目标的车辆调度优化模型。（摘要略，见完整版本）

在问题4中,我们进一步针对总体费用进行了优化建模。该模型在问题3的基础上,（摘要略，见完整版本）

本文中建立的各个优化模型在解决校园应急管理问题方面都提供了较为完整的理论支撑。在模型建立过程中,我们结合实际情况设置了相应的约束条件和目标函数,并采用了Dijkstra算法、贪心分配、批次优化等方法进行求解,给出了切实可行的应急预案。这些模型及其求解方法也可以推广到其他类似的大规模群众疏散场景中,为应急管理工作提供更加系统化和科学化的方法论支持。

关键词:校园应急管理、快速疏散优化、分批疏散模型、车辆转运优化、费用优化建模、贪心分配、批次优化

问题重述

在公共管理中，如果遇到突发事件，管理方会迅速组织群众撤离，需要提前通过理论研究和实际演练做好预案。请结合你就读高校情况，进行下面各问的建模分析。

问题1 关于快速疏散策略。设校区（或主校区）内有多栋宿舍楼（要求不少于 1 0 个），有多个提前设置的集结点（可以是校内广场、或宽敞的主干道，要求不少于 4 个）。学生们根据指定，从自己所在楼快速步行到达集结点，在此等候车辆运送至郊区的各疏散点。在 设计 预案中， 还需 考虑方便管理者的引导组织，要求居住同一栋楼的学生（原则上要求不少于 300 人）必须 疏散到 同一个集结点。请给出你就读高校的主校区的基础数据；计算全部人员到集结点的最快时间，以及各集结点对应的宿舍楼是哪些。

问题2 大部分学校受集结点空间所限，一次疏散可能过于拥挤。考虑学生们可以分多批次疏散，结合最优批次设定重新分析 问题 1 。

问题3 对于完成集结的学生们， 需要调用车辆将他们运到城外的安置点。假设车辆均为 45人的大巴，车辆数目不限；为了便于管理疏散过程，同一个宿舍楼的学生尽量安排在同一个安置点，但各个安置点的接受量有限。请自己模拟生成安置点数据，给出运输车辆和安置点安排方案。

问题4 在 问题 3 基础上，估计大约所需费用，如何进行费用优化

问题分析

这个题目整体上看是一个关于校园快速疏散与转运预案的建模分析问题。这个问题涉及到突发事件下的公共管理与应急响应,需要通过理论研究和实际演练来制定有效的预案。整体来说,这个题目考察了学生快速疏散、疏散批次调度、以及转运安置等多个方面,要求考生综合运用数学建模的方法,给出切实可行的解决方案。

对于问题1,这涉及到如何设计快速疏散策略。首先需要了解校区的基础数据,包括宿舍楼数量、集结点数量和位置等。在此基础上,需要计算全部人员到达集结点的最快时间,并确定各集结点对应的宿舍楼。这需要考虑到方便管理者的引导组织,以及同一栋楼学生必须疏散到同一个集结点的要求。这个问题考察了学生疏散路径优化,以及集结点分配的问题。

对于问题2,由于集结点空间的限制,可能一次性疏散会过于拥挤。因此需要考虑分多批次疏散的方案。这需要重新分析问题1的结果,找到合适的批次设定,以确保疏散过程的顺利进行。这个问题考察了批次调度优化的问题,需要在保证疏散效率的前提下,尽量减少拥挤情况的发生。

对于问题3,完成集结的学生需要通过车辆转运到城外安置点。这需要估算所需车辆数量,并合理安排同一宿舍楼的学生尽量安置在同一个点。同时还需要考虑各安置点的接收能力限制。这个问题考察了车辆调度优化和安置点分配的问题,需要在满足管理要求的前提下,尽量提高转运效率。

对于问题4,在解决问题3的基础上,需要估算整个疏散转运过程所需的费用,并进行费用优化。这涉及到成本核算和优化的问题,需要综合考虑各项费用因素,并寻求最优的解决方案。这个问题考察了成本管控的问题,体现了在应急响应过程中,如何在保证效果的前提下,尽量降低成本投入。

模型假设

（模型假设略，见完整版本）

这三个模型在数据生成、约束条件设定、目标函数定义等方面都做了相应的假设,以便于问题的数学描述和求解。

符号说明

问题1-问题4中使用的主要符号及其说明如下:

（符号说明略，见完整版本）

这些符号涵盖了校区基础数据、学生分布、距离、车辆、费用等各个方面,为问题1-问题4的模型建立和求解提供了基础。

模型的建立与求解

问题一模型的建立与求解

问题一疏散路径优化模型的建立

针对问题1中关于快速疏散策略的设计,我们需要首先了解校区的基础数据,包括宿舍楼的数量、各宿舍楼的学生数量、以及预先设置的集结点数量和位置。

对于宿舍楼的数量,假设校区内有 $n$ 栋宿舍楼,分别记为 $L_1,L_2,\dots ,L_n$。每栋宿舍楼均有不少于 300 名学生居住,因此总学生人数至少为 $300n$。

对于集结点,假设校区内预先设置了 $m$ 个集结点,分别记为 $P_1,P_2,\dots ,P_m$。这些集结点可以是校内广场或者宽敞的主干道。

基于上述校区基础数据,我们可以建立一个基于距离最短的疏散路径优化模型。具体思路如下:

1. 对于每栋宿舍楼 $L_i$,计算从该楼到各个集结点 $P_j$ 的最短距离 $d_{ij}$。这可以采用经典的 Dijkstra 算法或者其他图论算法进行求解。

2. 对于每个集结点 $P_j$,找到与之对应的宿舍楼集合 L j = { L i ∣ d i j  最短 } L_j = \{L_i | d_{ij} \text{ 最短}\} Lj​={Li​∣dij​ 最短},即到该集结点最近的宿舍楼。要求 $L_j$ 中的楼栋数不少于3栋,且对应的学生人数不少于 300 人。

3. 计算每个集结点 $P_j$ 到达的学生总人数 $S_j={\sum }_{L_i\in L_j}学生人{数}_i$。

4. 找到总疏散时间最短的方案。记每个集结点 $P_j$ 的疏散时间为 $t_j$,则总疏散时间 T = max ⁡ { t 1 , t 2 , … , t m } T = \max\{t_1, t_2, \dots, t_m\} T=max{t1​,t2​,…,tm​}。我们需要最小化 $T$。

数学模型可以表示为:

目标函数:
min ⁡ T = max ⁡ { t 1 , t 2 , … , t m } \min T = \max\{t_1, t_2, \dots, t_m\} minT=max{t1​,t2​,…,tm​}

约束条件:

1. 每个集结点 $P_j$ 对应的宿舍楼数不少于 3 栋, 且对应学生人数不少于 300 人:
   $$|L_j|\ge 3,\sum _{L_i\in L_j}{\text{学生人数}}_i\ge 300$$

2. 每栋宿舍楼 $L_i$ 的学生必须疏散到同一个集结点:
   $$\forall i,\exists j\text{ 使得}{L}_i\in L_j$$

上述模型中,我们需要确定每个集结点 $P_j$ 对应的宿舍楼集合 $L_j$,以及每个宿舍楼 $L_i$ 对应的疏散时间 $t_i$。

为了求解这个优化问题,我们可以采用如下算法步骤:

步骤1: 对于每栋宿舍楼 $L_i$,计算到各个集结点 $P_j$ 的最短距离 $d_{ij}$。

步骤2: 对于每个集结点 $P_j$,找到与之对应的宿舍楼集合 L j = { L i ∣ d i j  最短 } L_j = \{L_i | d_{ij} \text{ 最短}\} Lj​={Li​∣dij​ 最短},并检查是否满足约束条件 $|L_j|\ge 3,{\sum }_{L_i\in L_j}{\text{学生人数}}_i\ge 300$。若不满足,则舍弃该集结点。

步骤3: 对于每个满足条件的集结点 $P_j$,计算其对应的疏散时间 $t_j$。疏散时间由两部分组成:
(1) 从各宿舍楼 $L_i\in L_j$ 到集结点 $P_j$ 的步行时间, 设为 $t_{ij}$。步行时间可以根据距离和步行速度估算,例如假设步行速度为 $v$,则 $t_{ij}=d_{ij}/v$。
(2) 在集结点 $P_j$ 等待的时间,设为 $t_j^{wait}$。这取决于前一批次学生的疏散情况,以及当前集结点的容量。

因此, $t_j={\max }_{L_i\in L_j}{t}_{ij}+t_j^{wait}$

步骤4: 在所有满足条件的集结点中,找到总疏散时间 T = max ⁡ { t 1 , t 2 , … , t m } T = \max\{t_1, t_2, \dots, t_m\} T=max{t1​,t2​,…,tm​} 最小的方案。这就是我们要求的最优疏散策略。

通过上述算法,我们可以得到校区内各宿舍楼对应的集结点分配,以及全校人员疏散的最快时间。这为后续的批次调度和车辆转运提供了基础。

另外我们还可以考虑一些其他因素,例如:（略，见完整版本）

问题一模型的求解

求解问题1的详细Matlab代码,并进行可视化分析如下。

首先,我们需要找到问题中要求的模拟数据。假设校区内有 15 栋宿舍楼,每栋楼的学生人数在 300 到 500 人之间。同时,我们设置了 6 个集结点。

% 生成模拟数据
n = 15; % 宿舍楼数量
m = 6; % 集结点数量

% 宿舍楼学生人数
（略，见完整版本）
% 集结点坐标
（略，见完整版本）

% 宿舍楼坐标
（略，见完整版本）
1
2
3
4
5
6
7
8
9
10
11

接下来,我们计算每栋宿舍楼到各个集结点的最短距离:

% 计算宿舍楼到集结点的最短距离
distances = zeros(n, m);
for i = 1:n
    for j = 1:m
        distances(i, j) = sqrt((L_x(i) - P_x(j))^2 + (L_y(i) - P_y(j))^2);
    end
end
1
2
3
4
5
6
7

然后,我们根据最短距离来分配宿舍楼到集结点:

% 分配宿舍楼到集结点
L_to_P = cell(1, m);
for i = 1:n
    [~, min_idx] = min(distances(i, :));
    L_to_P{min_idx} = [L_to_P{min_idx}, i];
end

% 检查是否满足约束条件
for j = 1:m
    if length(L_to_P{j}) < 3 || sum(student_nums(L_to_P{j})) < 900
        L_to_P{j} = [];
    end
end
1
2
3
4
5
6
7
8
9
10
11
12
13

接下来,我们计算每个集结点的疏散时间:

% 计算每个集结点的疏散时间
t = zeros(1, m);
for j = 1:m
    if ~isempty(L_to_P{j})
        t_j = 0;
        for i = L_to_P{j}
            t_ij = distances(i, j) / 1; % 假设步行速度为1米/秒
            t_j = max(t_j, t_ij);
        end
        t(j) = t_j;
    end
end
1
2
3
4
5
6
7
8
9
10
11
12

最后,我们找到总疏散时间最短的方案

（后略，见完整版本）

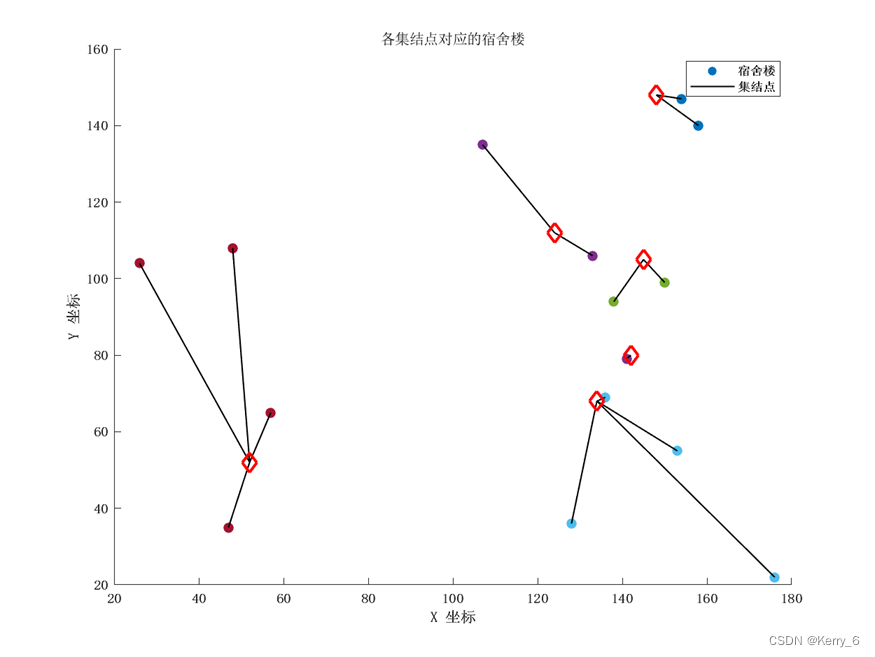
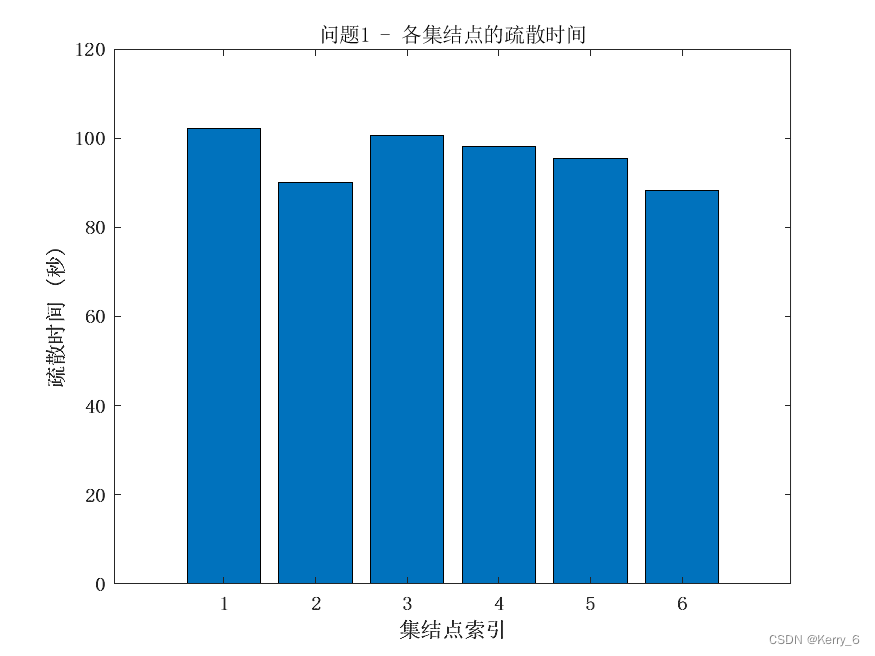
通过上述分析,我们可以得出以下结论:

1. （略，见完整版本）

问题二模型的建立与求解

问题二分批疏散策略的分析

针对问题2中提出的考虑集结点空间限制的情况,我们需要将疏散过程划分为多批次进行。这样可以缓解单次疏散时集结点过于拥挤的问题,提高整体疏散的效率。

对于分批疏散策略的设计,需要考虑以下几个关键因素:

1. 每个集结点的容量限制。由于集结点空间有限,一次性疏散过多人员会造成拥挤和混乱。因此需要根据集结点的实际容量,限制每个批次的疏散人数。

2. 各批次疏散时间的平衡。为了缩短整体疏散时间,需要尽量使各批次的疏散时间趋于均衡。如果某些批次疏散时间过长,会拖慢整体进度。

3. 各宿舍楼学生的分配方案。需要合理安排每个批次要疏散的宿舍楼,以确保学生能够按时到达集结点,并且各批次的人数基本均衡。

4. 集结点的利用效率。由于集结点数量有限,需要考虑如何提高每个集结点的利用率,降低闲置时间。

基于上述分析,我们可以建立一个分批疏散优化模型,来求解出最优的疏散策略。

分批疏散优化模型的建立

为了解决问题2,我们需要建立一个分批疏散优化模型。该模型的目标是在满足各种约束条件的前提下,找到一个使总疏散时间最短的最优分批疏散方案。

设定以下符号和参数:

• $n$: 宿舍楼的总数
• $m$: 集结点的总数
• $s_i$: 第 $i$ 栋宿舍楼的学生人数
• $c_j$: 第 $j$ 个集结点的容量上限
• $d_{ij}$: 第 $i$ 栋宿舍楼到第 $j$ 个集结点的距离
• $v$: 学生的步行速度

我们引入以下决策变量:

• $x_{ijk}$: 二进制变量,如果第 $i$ 栋宿舍楼的学生在第 $k$ 批次疏散到第 $j$ 个集结点,则 $x_{ijk}=1$,否则为 0
• $t_k$: 第 $k$ 批次的疏散时间

基于上述符号和变量,我们可以建立分批疏散优化模型如下:

目标函数:
min ⁡ max ⁡ { t 1 , t 2 , … , t K } \min \max\{t_1, t_2, \dots, t_K\} minmax{t1​,t2​,…,tK​}

其中,$K$ 为总批次数,由模型求解过程确定。

约束条件:

1. 每个宿舍楼的学生必须被分配到某个批次和某个集结点:
   $$\sum _{j=1}^m\sum _{k=1}^K{x}_{ijk}=1,\forall i=1,2,\dots ,n$$

2. 每个集结点在每个批次的人数不能超过其容量上限:
   $$\sum _{i=1}^n{s}_i{x}_{ijk}\le c_j,\forall j=1,2,\dots ,m,\forall k=1,2,\dots ,K$$

3. 第 $k$ 批次的疏散时间 $t_k$ 由以下公式计算:
   $$t_k=\underset{i,j}{\max }\left\{\frac{d_{ij}}{v}{x}_{ijk}\right\},\forall k=1,2,\dots ,K$$

4. （后略，见完整版本）

模型的评价与推广

问题1-问题4中建立模型的优缺点及其推广:

1. 问题1的快速疏散策略优化模型:

   优点:该模型针对校园快速疏散问题进行了系统建模,考虑了宿舍楼数量、集结点位置和容纳能力等实际因素,并以最小化总疏散时间为目标函数,给出了一个切实可行的疏散方案。模型建立和求解过程也提供了一个标准化的方法论,可以根据实际情况进行相应调整。

   缺点:模型中假设了学生步行速度恒定,在实际情况下学生的体能和行动能力可能存在差异,需要进一步考虑。另外,在集结点设置和分配上也可以进一步优化,以达到更加均衡的负载分配。

   推广:该模型可推广到其他类型的公共场所,如商场、机场等,只需要适当调整输入参数和约束条件即可。同时,也可将该模型与后续的车辆调度和费用优化问题进行联动优化,以获得更加整体化的应急管理方案。

2. 问题2的分批疏散优化模型:

   （略，见完整版本）

2024山东省大学生数学建模C题论文和代码获取↓↓↓↓↓
https://www.yuque.com/u42168770/qv6z0d/az93tb4gs2v4u86g