路径规划——搜索算法详解（七）：D*lite算法详解与Matlab代码_d*lite算法代码实现

！！！注意！！！

看本篇之前，一定要先看笔者上一篇的LPA*讲解，笔者统一了符号看起来过渡会更加好理解！

到目前为止，我们学习了广度优先搜索Dijkstra算法、能够计算任意两个路径点距离的Floyd算法、基于采样实现快速计算的RRT算法、能够利用启发项加速探索过程的A*算法、适用于动态环境反向搜索的D*算法、增量式动态搜索的A*——LPA*算法，每种算法都有其特点，大家根据需求选择就好。

无独有偶，上述6种路径搜索算法仅适用于处理起点与终点固定情况下的路径搜索问题，本文将介绍搜索算法篇的最后一种算法——D*lite算法，该算法基于D*反向搜索的思想、LPA*增量式搜索的思想，是一种变起点反向增量式动态路径搜索算法，接下来便进入正题吧，老规矩分为算法介绍与案例讲解。（PS：搜索算法部分总结完后将开启路径优化的篇章，将介绍各种拟合轨迹的曲线，并且给出能够直接采用的C++代码，需要的朋友可以关注后续！)

一、D*lite算法流程：

1.与LPA*算法的联系与区别：

其算法原理与LPA*算法类似（没有看的朋友先看我上一篇LPA*算法的讲解再来看，因为里面定义的符号含义需要理解，不然看不懂的！！！），其改进了LAP*中的代价项k，增加了机器人当前实际移动距离km（机器人位置移动可以看作是起点位置移动了），其定义如下：

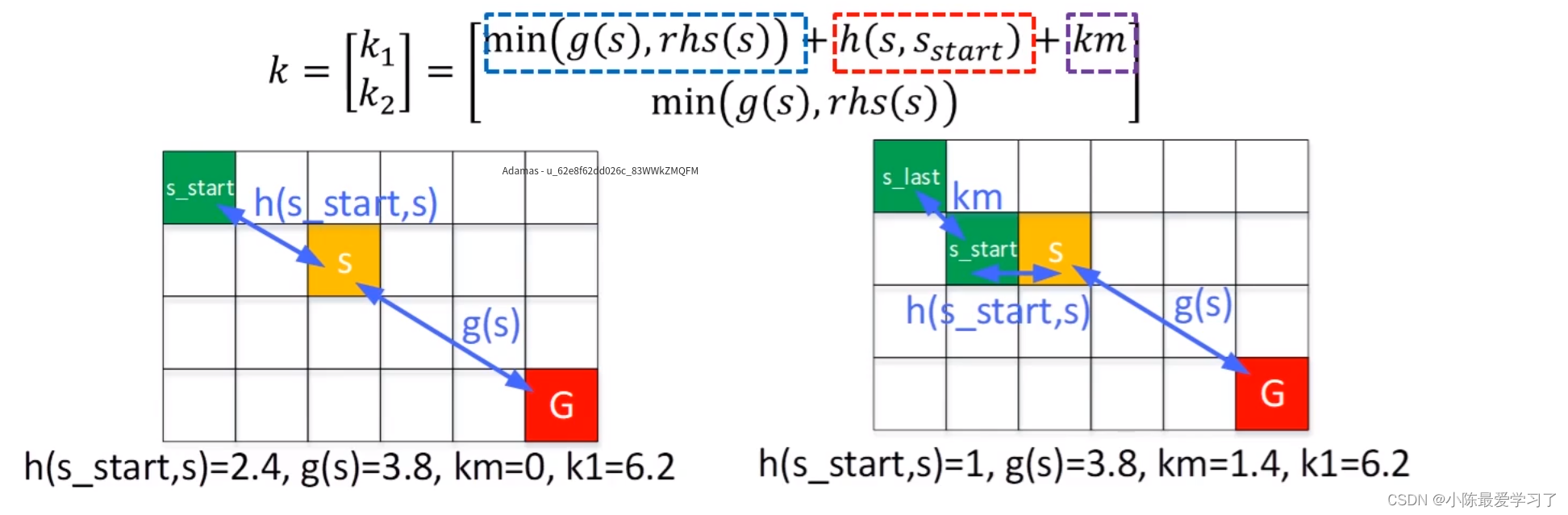
如上图所示S（黄色）为当前遍历节点，G（红色）为终点位置，绿色为机器人所在的位置（可以看作是路径搜索的起点），如左图所示，g(s)为终点距离所记录的最小代价值，rhs(s)为搜索过程中所更新计算的当时的终点距离代价值，对角移动距离为1.4，直接连接距离为1，通过计算即可得到对应的值。当机器人移动到新的s_star时原位置点标记为s_last，此时h变为1，km更新为1，左右图k1值保持不变，计算结果如上图2所示。

上述就是k值更新过程中与LPA*算法的区别，此外流程上相差并不大，大致框架相同，稍后会进行讲解。但由于k值计算方式的不同会产生新的问题：机器人每移动一步，km实时发生变化，此时对于每一个节点都需要更新其k1值。当当前优先队列U中节点较多的时候，每运动一步都需要更新，这会增加计算负担。

本算法提出了一种解决方案，当机器人起点位置发生改变后，与其减去原优先队列U中每一个节点的h值，不如直接将新插入队列的节点加上km值（如上两个图所示，h减少的数值正好等于km所增加的数值），这样就不会影响U节点中的弹出顺序，并且节省计算资源。

2.算法代码框图：

符号含义如下所示：

• g(s)：之间记录的起点距离代价的最小值；
• rhs(s)：基于父节点g所预测的最小值，设s'为s的父节点，此时有rhs(s)=g(s')+d(ss')，d(ss')表示s与父节点s‘的连接代价，由于D*lite为反向搜索的算法，所以父节点指的是离终点近的路径点。
• K：代价值，与LPA*不同，其K（包含k1、k2）计算如下所示：

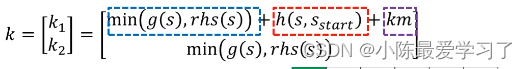
• S：地形图中路径点集合
• U：优先队列，每次弹出k值最小的节点s；

其函数包含初始化部分（Initialize）、计算路径部分（ComputeShortestPath）、更新节点部分（UpdateVertex）、计算代价部分（CalculateKey），直接看估计会蒙圈，下面将通过一个例子讲解该算法的更新过程

3.D*lite算法案例讲解：

1.地图介绍：

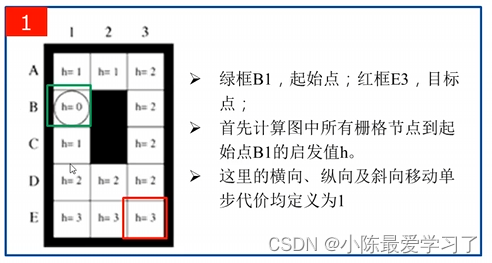
搜索地图如上图所示，其中B1为起点，E3为目标点，在地图预处理时，根据设定的启发函数（如曼哈顿距离、欧氏距离、切比雪夫距离）等计算出每一个点的启发值h，规定直线距离、对角移动距离均为1。

2.初始化（起点可以看作是第1次循环）：

初始化代码如Initialize函数(02-06行)所示，首先将优先队列U初始化为空，初始化机器人运动距离km=0（即机器人当前没有发生移动，起点没有发生运动）。初始化所有节点集合S中的所有节点终点最小距离g(s)与实时计算终点距离rhs(s)为无穷大。将起点rhs置为0，并且将其插入到优先队列中U中启动搜索。

此时U={E3}，此时g(E3)=∞、rhs(E3)=0、h(E3)由上一步计算为3，此时k(E3)=[0+3+0,0]=[3,0]，接下来执行代码中的步骤2——ComputeShortestPath（代码10-20行），进图while循环（当且仅当搜索起点达到局部一致且弹出的k值大等于起点的k值时才跳出循环）

首先从U中弹出k值最小的节点，此时U中只有E3，此时CalculateKey(E3)=[3,0]=kold(E3)，跳到代码15行进行判断，得到g(E3)=∞ > rhs(E3)=0，满足条件，执行16-17行的代码，此时更新g(E3)=rhs(E3)=0，E3达到局部平衡，标记为0。此外，遍历所有周围节点中的父节点（此处规定距离起点近的为父节点），即D2、E2、D3。

3.拓展节点（第2次循环）：

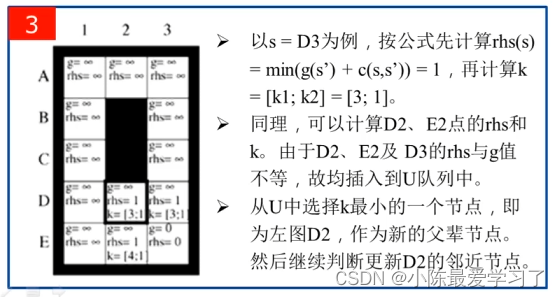
遍历D2、E2、D3分别带入UpdateVertex函数中（代码07-09行），根据其子节点E3更新rhs值：如rhs(D2)=1(D2与E3的连接代价)+g(E3)=1+0=1，同样可以计算的到rhs(E2)=1、rhs(D3)=1，判断其是否为局部一致（08行代码），由于初始化g值均为∞，D2、E2、D3均为局部过一致状态，此时计算其k值，并将其加入到优先级队列U中，这步结束后U={D2[3,1],E2[4,1],D3[3,1]}。

4.拓展节点（不断循环，得到起点没有变化时的最终路径）：

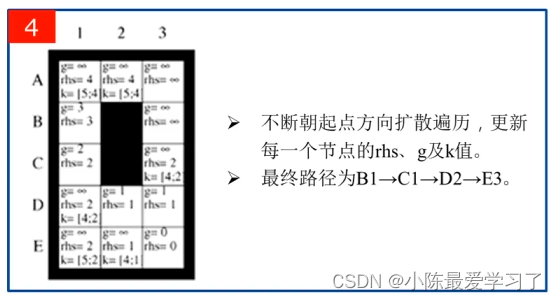
不断循环（上面的步骤跟LPA*算法几乎一样，只是搜索方向上是反过来的，LPA*从起点开始而D*lite从终点开始，还是不难理解的） ，得到如上图所示的结果，此时满足循环跳出的条件，得到最终路径为B1-C1-D2-E3。跳出步骤2，主函数中的ComputeShortestPath部分执行结束（代码23行）

5.起点变换时候的处理：

如左图所示，此时机器人位置由B1变为了C1，D2变为了障碍物，执行24-35行的代码。

当起点与终点不为同一节点时候进入该循环，首先更新所有节点与当前新起点的启发值，计算新的km值km(new)=km+h(s_start,s_last)=0+1=1（代码第30行），此时检查受影响的节点，扩散其变化造成的影响（代码32-34行），详细执行更新代价步骤如下所示：

如图6-1所示，D2变为障碍物rhs(D2)=inf，由于C1与D2直接相连（代码第32行），C1的rhs值受到影响变rhs(C1)=d(D1与C1之间的距离)+g(D1)=1+inf=inf。同理找出C1的子节点，并更新其rhs值，rhs(D1)=rhs(E1)=inf，这便是更新障碍物的传递过程（代码第33行）。

此时C1检查周围节点，查找能够将rhs(C1)值变为最小的节点作为父节点（代码第34行，跳到步骤4），此时将B1作为父节点能够使得rhs(C1)=3+1=4，与g(C1)=2不相等为局部欠一致，将其重新插入到队列U中（代码09行） ，同理将D1、E1也加入到队列U中。

更新完所有受到影响的节点后，再次调用路径搜索函数（代码第35行）重复2-4的步骤，即可得到新的路径为C1-D1-E2-E3。

该算法的奇妙之处在于在起点更新后更新了h值，能够启发新一轮的搜索，大家可以这样理解，一旦节点的起点发生变化，基于起点求解得到的每一个节点的h值肯定会发生改变，这工作量是巨大的，这是LPA*算法不能用于变起点搜索的主要原因。为了减少计算量，我们无需在原有的节点上减去h值，而是维护一个由于起点位置更改而受影响km值，km值可以理解为我们原本需要更新在原来每一个节点上h值的差值，原本我们需要在每一个节点h中加或者减km，此时我们只需要在新更新的节点上减或者加上这个差额，维持其相对的大小顺序，妙哉！

二、D*lite算法MATLAB代码

这是笔者按照古月的课程打出来的代码，已经上传到了本人Github，需要的自取：

Adamaser/Path-Planning (github.com)