自然语言处理——TF-IDF文本表示_句子的tf-idf

引言

在文本的表示中，我们已经介绍了基于计数(Count-based Representation)的文本表示方法，为什么还要介绍TF-IDF文本表示法呢。

在一句话里面有很多停止词，通常这些停止词出现的次数很多。

只要是个英文网站都会用到a或者是the。 在中文网站里面其实也存在大量的停止词。比如，我们前面这句话，“在”、“里面”、“也”、“的”、“它”、“为”这些词都是停止词。——百度百科

如果采用基于计数的文本表示方法，会给停止词很大的频次，从而可能会影响我们计算文本相似度的结果。tf-idf就能解决这个问题。

tf-idf

我们先来看下tf-idf(Term Frequency-Inverse Document Frequency, 词频-逆文档频率)的公式。

tf-idf是由两部分组成的：

tf-idf(w) = tf(d,w) * idf(w)

tf是文档d中w的词频，也就是单词出现的次数，但是文档有长短之分，为了比较不同的文档，需要做"词频"标准化，即 (w在文档d中出现的次数 / 文档d的总单词数)。

idf是逆文档频次，说的是如果包含单词w的文档越少，则idf越大，说明单词w具有很好的类别区分能力，越重要。

$idf=\log \frac{N}{N(w)}$

• 其中$N$是语料库中的文档总数
• $N(w)$是包含单词$w$的文档数

之前的停用词，很多出现在大多数的文档(句子)中，因此$N(w)$很大，也就是分母很大，idf就较小。加了$log$是防止idf过大。

下面我们通过一个例子来计算一下td-idf。

首先定义我们的词典：

word_dic = ['今天','上','NLP','的','课程','有','意思','数据','也']
1

假设我们有这样三个分好词的句子：

$S_1$：“今天/上/NLP/课程”
$S_2$：“今天/的/课程/有/意思”
$S_3$：“数据/课程/也/有/意思”

那么如何计算句子的tf呢？

先看$S_1$中第一个单词“今天”，也是词典中的第一个单词：

$\frac{1}{4}\cdot \log \frac{3}{2}$

$S_1$的单词数为$4$，“今天”出现的次数为$1$，tf为$\frac{1}{4}$；
文档总数$N$为$3$，包含“今天”的文档数为$2$，idf为$\log \frac{3}{2}$。

然后再看词典中的第二个单词“上”：
“上”出现的次数为$1$，tf为$\frac{1}{4}$；
包含“上”的文档数为$1$，idf为$\log \frac{3}{1}$。

接着看词典中的第三个单词“NLP”：
“NLP”出现的次数为$1$，tf为$\frac{1}{4}$；
包含“NLP”的文档数为$1$，idf为$\log \frac{3}{1}$。

再看词典中的第四个单词“的”：
“的”没有在$S_1$中出现，因此tf-idf为0。

再看词典中的第五个单词“课程”：
“课程”出现的次数为$1$，tf为$\frac{1}{4}$；
包含“课程”的文档数为$3$，idf为$\log \frac{3}{3}$。

接下来词典中的其他单词没有在$S_1$中出现，因此tf-idf都为0。
这样我们得到了第一个句子的tf-idf表示：
$(\frac{1}{4}\cdot \log \frac{3}{2},\frac{1}{4}\cdot \log \frac{3}{1},\frac{1}{4}\cdot \log \frac{3}{1},0,\frac{1}{4}\cdot \log \frac{3}{3},0,0,0,0)$

tf-idf向量的维度也是和词典大小一致的。

下面直接给出句子$S_2$的tf-idf向量：
$(\frac{1}{5}\cdot \log \frac{3}{2},0,0,\frac{1}{5}\cdot \log \frac{3}{1},\frac{1}{5}\cdot \log \frac{3}{3},\frac{1}{5}\cdot \log \frac{3}{2},\frac{1}{5}\cdot \log \frac{3}{2},0,0)$

出句子$S_3$的tf-idf向量：
$(0,0,0,0,\frac{1}{5}\cdot \log \frac{3}{3},\frac{1}{5}\cdot \log \frac{3}{2},\frac{1}{5}\cdot \log \frac{3}{2},\frac{1}{5}\cdot \log \frac{3}{1},\frac{1}{5}\cdot \log \frac{3}{1})$

这样我们就得到这三个句子的tf-idf向量。

下面通过代码实现一下。

TF-IDF代码实现

word_dic = ['今天','上','NLP','的','课程','有','意思','数据','也']
s1 = '今天上NLP课程'
s2 = '今天的课程有意思'
s3 = '数据课程也有意思'
1
2
3
4

首先是我们的词典和三个句子。

def cut_words(segment,word_dic,max_len=3):
    seg_list = []
    i = len(s1)
    while i > 0:
        for pos in reversed(range(max_len)):
            if i >= pos + 1:
                if segment[i-pos-1:i] in word_dic:
                    seg_list.append(segment[i-pos-1:i])
                    i = i - pos
                    break
        i = i -1
    return list(reversed(seg_list))
1
2
3
4
5
6
7
8
9
10
11
12

然后基于这个词典实现一个分词算法。

# 先进行分词
s1_words = cut_words(s1,word_dic)
s2_words = cut_words(s2,word_dic)
s3_words = cut_words(s3,word_dic)

print("/".join(s1_words))
print("/".join(s2_words))
print("/".join(s3_words))

# 构建数据集
data_set = [s1_words,s2_words,s3_words]
data_set
1
2
3
4
5
6
7
8
9
10
11
12

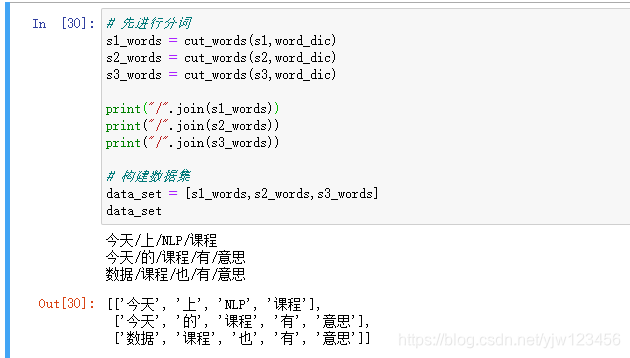
用我们实现的分词算法来进行分词，刚好可以得到上一节例子中的结果。

接下里就开始实现TF-IDF算法了。

from collections import defaultdict
from collections import Counter
from math import log

def compute_tfidf(data_set,word_dic):
    '''根据传入的data_set和word_dic，计算data_set中每个句子的tfidf向量'''
    N = len(data_set) #文档的总数
    N_w = defaultdict(int) #包含单词w的文档数,通过字典来缓存计算结果
    
    for w in word_dic:
        for segment in data_set:
            if w in segment:
                N_w[w] += 1
 
    
    tfidfs = []#返回的结果
    for segment in data_set:
        # 每个句子
        c = Counter(segment)
        N_S = len(segment) #文档的单词总数
        result = []
        for w in word_dic:
            if w not in c:
                result.append(0)
                print('0 ',end='')
            else:
                tf = c[w] / N_S                    
                idf = log(N / N_w[w])
                result.append(tf * idf)
                print('%i/%i*log(%i/%i) ' %(c[w],N_S,N,N_w[w]),end ='')
        print()
        tfidfs.append(result)
    return tfidfs
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

这里是针对上节介绍的原理一个简单实现，没有考虑N_w为零的情况，效率也有一定的问题，不过作为理解原理足够了。

在计算的过程中增加了一个调试信息，可以看到和上节我们手写的结果是一样的。

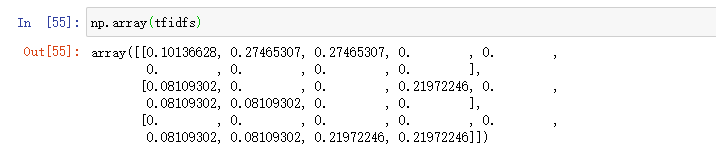
计算的结果如上所示。

然后我们实现一下欧几里得距离和余弦相似度计算公式。

import numpy as np

def euclid_dis(v1,v2):
    v1 = np.array(v1)
    v2 = np.array(v2)
    return np.sqrt(np.sum( (v1 - v2)**2))

def cosine_similarity(v1,v2):
    v1 = np.array(v1)
    v2 = np.array(v2)
    return (v1.dot(v2)) / (np.linalg.norm(v1) * np.linalg.norm(v2))
1
2
3
4
5
6
7
8
9
10
11

基于numpy是很简单的。

print('s1 and s2 euclid_dis:%.2f , cosine_similarity:%.2f' % (euclid_dis(tfidfs[0],tfidfs[1]),cosine_similarity(tfidfs[0],tfidfs[1])))
print('s1 and s3 euclid_dis:%.2f , cosine_similarity:%.2f' % (euclid_dis(tfidfs[0],tfidfs[2]),cosine_similarity(tfidfs[0],tfidfs[2])))
print('s2 and s3 euclid_dis:%.2f , cosine_similarity:%.2f' % (euclid_dis(tfidfs[1],tfidfs[2]),cosine_similarity(tfidfs[1],tfidfs[2])))
1
2
3

最后从打印结果可知，句子“今天的课程有意思”和“数据课程也有意思”是最相似的，这也符合我们的直觉。

参考

1. 贪心学院课程