十五、计算机视觉-sobel算子

前言

上节课我们学习了梯度的知识，学习了如何去计算梯度，本节我们继续学习计算梯度的方法，本节我们学习使用Sobel算子计算梯度，这与上节课梯度计算方法有所不同，一般如果需要准确地计算图像的梯度信息，特别是对边缘信息感兴趣，通常会选择Sobel、Scharr或Laplacian算子。而如果更关注形态学特征或者想要一种简单快速的边缘检测方法，可以考虑使用cv2.morphologyEx。

一、sobel算子的概念

Sobel算子是一种用于图像边缘检测的经典算法。它基于一种称为梯度的数学概念，用于找到图像中灰度变化较大的地方，通常表现为图像中的边缘或轮廓。
Sobel算子通过在图像上应用两个3×3的卷积核（或称为模板）来计算图像的梯度，这两个卷积核分别用于检测图像中水平和垂直方向的变化。
这些卷积核的设计是为了捕捉图像中的灰度变化，使得在卷积过程中离边缘更近的像素权重更大，从而突出边缘特征。通过计算图像中每个像素点的水平和垂直方向的梯度，Sobel算子能够有效地检测图像中的边缘。

二、sobel算子的计算方式

上面提到sobel算子是通过一个3x3的卷积核来计算图像梯度，卷积核我们前面已经有过了解了。在这里卷积核是什么内容呢？
我们首先看下Sobel算子的计算公式：

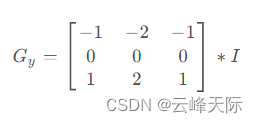
sobel算子包括两个3×3的卷积核，分别用于计算图像在水平和垂直方向上的梯度。
Gx是水平方向的梯度，Gy是垂直方向的梯度，最终2个值的绝对值相加就是最终的梯度结果。
这2个卷积核的内容如下：

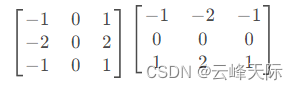
我们来分析一下这个公式：卷积核内容为什么要这样设置，以及这个公式为什么这样计算，有什么底层的逻辑。
首先我们看下横向梯度的计算方式，假如卷积核覆盖的图像像素点如下：

那结合上面的横向卷积核的内容 他的计算公式为：(p3-p1)+(2p6-2p4)+(p9-p7).
而卷积核的内容实际上是代表的权重。比如离中心点越近权重越高。因为我们目的是进行边缘检测，而边缘通常指的是图像中灰度变化较大的地方，而像素值的变化通常发生在边缘附近。通过将离中心点最近的像素的权重设置为2或-2，可以加大边缘处灰度变化对卷积结果的影响，从而更好地突出边缘特征。如下图：（实际卷积核不是图示这么大 图只是为了方面演示查看）
和之前课程中讲到的卷积核一样，卷积核在图像上移动

当我么卷积核范围没有灰度变化时，通过公式计算就没有产生梯度，一旦当卷积核范围产生了灰度变化 比如

通过上面公式我们计算卷积核中心点位置 也就是图像p5的位置 就有值了。
当卷积核在移动到没有灰度变化的地方 就不会产生梯度

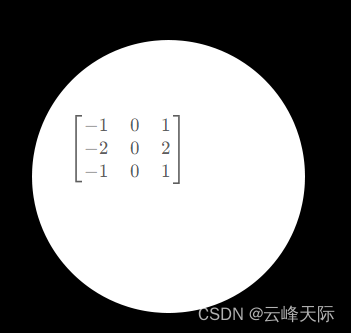
现在有个问题：当卷积核移动到图像右边边缘时

按照我们的计算公式，右边减左边，在这个位置右边减左边肯定是小于0了，默认opencv处理是小于0的就置为0 但是我们右边也有边缘置为0就是看不到边缘了，不符合我们的要求了，那怎么办呢。在回到上面的公式

这就是我们使用绝对值的原因。

纵向方向的梯度和横向方向的梯度原理都是一样的，只不过纵向方向的是下面的减去上面的
(p9-p3)+(2p8-2p2)+(p7-p1)。通过纵向计算同样得到一个边缘。2个边缘相加就是我们的最终结果。纵向这里就不在演示了。那有人可能问了，我们为什么要分别计算纵向和横向，既然纵向和横向都可以获取边缘信息，我们为何不只使用其中一种方式，或者2种方式同时使用，而不是单独计算在相加？
其实你自己实际测试一下就知道原因了，这种方式可以更好地捕捉图像中的边缘信息。虽然理论上可以设计一个3×3的卷积核同时计算水平和垂直方向的梯度，但在实践中，分别计算水平和垂直方向的梯度更为常见且更有效。分别计算水平和垂直方向的梯度可以提供更多的方向信息，使得边缘检测更加准确。例如，当图像中的边缘是斜向的时候，水平和垂直方向的梯度可以更好地捕捉到这种特征。

三、具体实现

import cv2

# 读取图像
image = cv2.imread('yunfeng.jpg')

# 转换为灰度图像
gray_image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

# 使用Sobel算子计算水平方向和垂直方向的梯度
grad_x = cv2.Sobel(gray_image, cv2.CV_64F, 1, 0, ksize=3)
grad_y = cv2.Sobel(gray_image, cv2.CV_64F, 0, 1, ksize=3)

# 计算梯度的幅值
gradient_magnitude = cv2.magnitude(grad_x, grad_y)

# 显示结果
cv2.imshow('Original', image)
cv2.imshow('sobel', cv2.convertScaleAbs(gradient_magnitude))

cv2.waitKey(0)
cv2.destroyAllWindows()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

其中cv2.Sobel是计算梯度信息，cv2.Sobel(gray_image, cv2.CV_64F, 1, 0, ksize=3)
第一个参数是输入的图片信息，
第二个参数是图像数据类型，Sobel算子的计算中，我们通常会使用CV_64F作为数据类型，以便在计算过程中保持足够的精度。64位浮点数格式可以处理更大范围的数值，以及更高的精度，有助于避免在计算过程中出现数值溢出或失真的情况
第三个参数是1代表计算横向的梯度
第四个参数是0代表不计算纵向的梯度
第五个参数是卷积核大小

cv2.magnitude就是我们上面提到的公式的实现方法

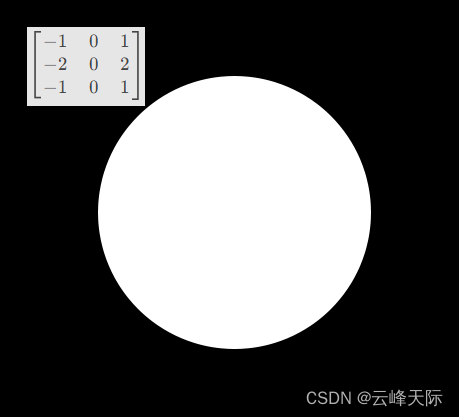
我们看下最终的结果