数据结构之最小堆[MinHeap]（C#版）

什么是最小堆

猿话版

1. 最小堆是一棵小根树，节点的值都小于等于其根节点的值；
2. 最小堆是完全二叉树；

补充一点： 什么是完全二叉树？

完全二叉树的官方定义，这里就不复制粘贴咯，因为太难理解了
（至少对于我来说…），所以，这里就补充一下，我个人是怎么理解完全二叉树的。

个人理解的完全二叉树：添加元素时，只能往最后一层（如果最后一层已经满了，则从下一层开始）按照从左到右的顺序进行添加。

下面用图示解释一下：

下图所示的是一棵完全二叉树，先来看看如何往这棵树里面插入元素才能维持完全二叉树的属性。

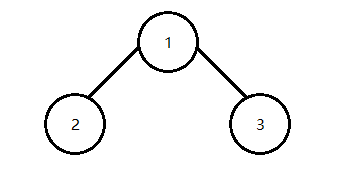
插入一个元素后的完全二叉树应如下图所示：

可以看到，第二层已经满了，所以需要往下一层添加，因为第三层是没有元素的，所以要从第一个位置（即节点2的左节点）开始添加，好，下面个我们再来添加一个元素，让它继续是一棵完全二叉树。

现在插入了元素5，它仍是一棵完全二叉树，其实，树在添加元素的时候，按照图上的箭头方向来添加元素，就是一棵完全二叉树了。

说了那么多，我们来看看，怎么插入元素，能让它毁掉完全二叉树的威名。

从上图可以看到，如果将元素6放到红色的位置，那么它仍然是一棵完全二叉树，可是呢，元素6不听话，说要毁掉这棵完全二叉树的威名，于是它站到了黑色的位置，那么这棵树，就不是完全二叉树了。

代码

最小堆的结构

实现最小堆其中之一的结构，就是使用动态数组（列表），这种实现方式，跟之前使用类的方式去实现的其他树有所不同。最大的不同点是，对于动态数组的方式，我们如何确定或者说定位一个元素的子节点或者父节点呢？

我们先来看个图吧。
最小堆和动态数组的对应关系如上图。

废话不多说，看图可以得出（哈哈哈哈），假设当前元素的索引为n，其左子节点索引为2*n+1，其右子节点索引为2*n+2，其父节点为 (n-1)/2（取整）。

下面就看看代码吧。

public class MinHeap<T> where T : IComparable
    {
   
        ///<summary>
        /// 储存元素的List
        ///<summary>
        private List<T> _elements;
        ///<summary>
        /// 堆元素数量
        ///<summary>
        public int Count
        {
   
            get {
    return _elements.Count; }
        }
        ///<summary>
        /// 构造函数
        ///<summary>
        public MinHeap()
        {
   
            _elements = new List<T>(
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22