devbox
在线问答5
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

【数据结构与算法】之顺序表及其实现！_设计算法实现顺序表入和出

作者：在线问答5 | 2024-07-12 05:18:11

赞

踩

设计算法实现顺序表入和出

目录

​编辑

1. 顺序表的概念及结构

2. 接口的实现

2.1 顺序表的初始化

2.2 检查顺序表容量是否已满

2.3 顺序表的尾插

​编辑

2.4 顺序表的尾删

2.5 顺序表的头插

2.6  顺序表的头删

2.7 顺序表在pos位置插入

2.8  顺序表在pos位置删除

2.9 顺序表的查找

2.10 顺序表的销毁

2.11 顺序表的打印

 3. 我在实现顺序表时的测试代码

4. 完结散花

                                                                                个人主页：秋风起，再归来~

                                                                                            数据结构与算法                             

                                                                       个人格言：悟已往之不谏，知来者犹可追

                                                                                        克心守己，律己则安！

1. 顺序表的概念及结构

顺序表是用一段物理地址连续的存储单元以此存储数据的线性结构，一般情况下用数组存储。在数组上完成数据的增删查改~

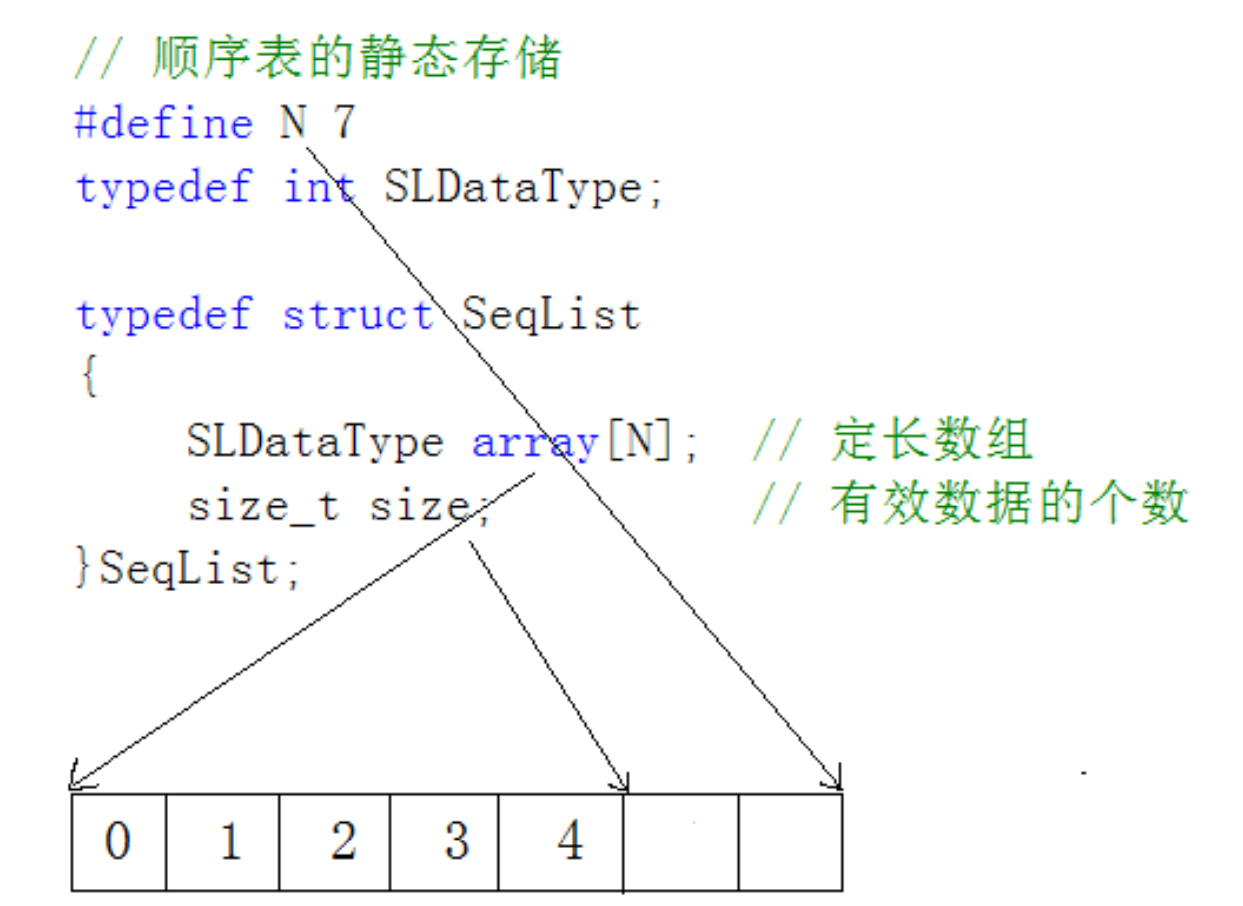
1. 静态顺序表:用指定长度数组存储元素~

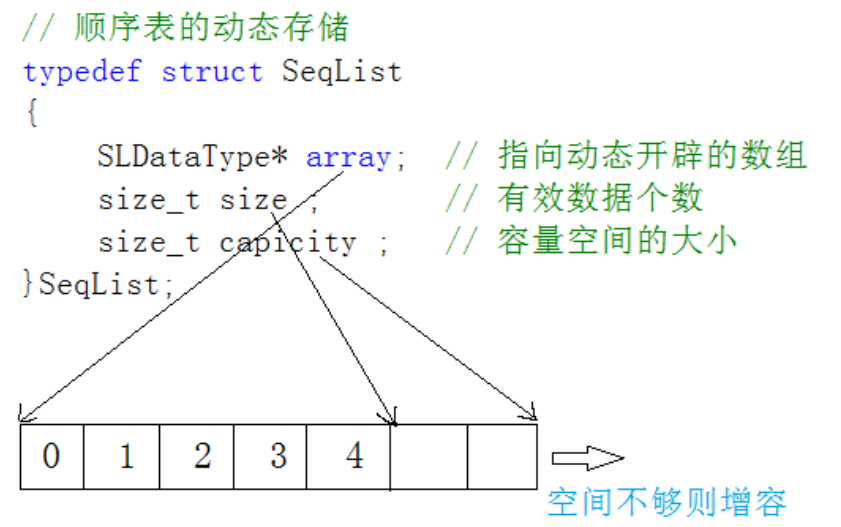
2. 动态顺序表:用动态开辟的数组存储~

2. 接口的实现

静态顺序表只适用于确定知道需要存多少数据的场景。静态顺序表的定长数组导致N定大了，空 间开多了浪费，开少了不够用。所以现实中基本都是使用动态顺序表，根据需要动态的分配空间 大小，所以下面我们实现动态顺序表。

我们创建一个Test.h里面包含了所有的接口函数声明和各种头文件的声明~

这样我们一个一个实现，正所谓天下难事必做于细~

  1. #define _CRT_SECURE_NO_WARNINGS
  2. #pragma once//避免头文件的多次包含
  3. #include<stdio.h>
  4. #include<assert.h>
  5. #include<stdlib.h>
  6. typedef int SLDataType;//便于类型的改动
  7.  
  8. //定义一个动态顺序表的结构体变量
  9. typedef struct SeqList
  10. {
  11. 	SLDataType* arr;
  12. 	size_t num;//记录有效数据的个数
  13. 	size_t capacity;//该顺序表的容量大小
  14. }SL;//将该结构体类型重命名为SL
  15.  
  16. //加入增删查改接口
  17.  
  18. //1. 顺序表初始化
  19. void SeqListInit(SL* p);
  20.  
  21. //2. 检查顺序表容量是否已满
  22. void CheckSeqList(SL* p);
  23.  
  24. //3. 顺序表的尾插
  25. void SeqListPushBack(SL* p, SLDataType x);
  26.  
  27. //4. 顺序表的尾删
  28. void SeqListPopBack(SL* p);
  29.  
  30. //5. 顺序表的头插
  31. void SeqListPushFront(SL* p, SLDataType x);
  32.  
  33. //6. 顺序表的头删
  34. void SeqListPopFront(SL* p);
  35.  
  36. //7. 顺序表在pos位置插入
  37. void SeqListInsert(SL* p, size_t pos,SLDataType x);
  38.  
  39. //8. 顺序表在pos位置删除
  40. void SeqListErase(SL* p, size_t pos);
  41.  
  42. //9. 顺序表的查找
  43. int SeqListFind(SL* p,SLDataType x);//如果该数字存在则返回该数字的下标，否则返回-1
  44.  
  45. //10 顺序表的销毁
  46. void SeqListDestory(SL* p);
  47.  
  48. //11. 顺序表的打印
  49. void SeqListPrint(SL* p);

我们将所有函数的实现放在SeqList.c文件中~

2.1 顺序表的初始化

(1) 代码实现
  1. //1. 顺序表初始化
  2. void SeqListInit(SL* p)
  3. {
  4. 	assert(p);//判断指针的有效性
  5. 	p->arr = NULL;
  6. 	p->capacity = 0;
  7. 	p->num = 0;
  8. }
(2) 复杂度分析
  • 时间复杂度：由于没有其他未知数的引入，所以所需时间是个常数，也就是O(1)。
  • 空间复杂度：动态开辟N个空间，所以空间复杂度为O(N)。

 注意我们这里一定要传址调用~

2.2 检查顺序表容量是否已满

(1) 代码实现

 注释写的很详细了，这里就不做过多的解释~

  1. //2. 检查顺序表容量是否已满
  2. void CheckSeqList(SL* p)
  3. {
  4. 	assert(p);//判断指针的有效性
  5. 	if (p->num == p->capacity)
  6. 	{
  7. 		 size_t newcapacity=p->capacity == 0 ? p->capacity = 4 : p->capacity * 2;
  8. 		//如果原来没有空间，就给上4，有的话就扩大为原来的两倍
  9. 		 SLDataType* ptr = (SLDataType*)realloc(p->arr, newcapacity * sizeof(SLDataType));//动态扩容
  10. 		 if (ptr == NULL)
  11. 		 {
  12. 			 perror("realloc fail;");
  13. 			 return;
  14. 		 }
  15. 		 //也可以用assert断言一下
  16. 		 p->arr = ptr;//开辟成功将地址传给arr
  17. 		 p->capacity = newcapacity;//更新容量
  18. 	}
  19. }

2.3 顺序表的尾插

(1) 代码实现
  1. //3. 顺序表的尾插
  2. void SeqListPushBack(SL* p, SLDataType x)
  3. {
  4. 	assert(p);//判断指针的有效性
  5. 	CheckSeqList(p);//尾插前先判断有没有容量或容量够不够
  6. 	p->arr[p->num] = x;//尾部插入数据
  7. 	p->num++;//有效数加一
  8. }

(2) 复杂度分析
  • 时间复杂度：没有变量影响时间，时间复杂度为O(1)。
  • 空间复杂度：以最坏的情况考虑，会进行扩容，空间复杂度为O(N)。

2.4 顺序表的尾删

(1) 代码实现
  1. //4. 顺序表的尾删
  2. void SeqListPopBack(SL* p)
  3. {
  4. 	assert(p);//判断指针的有效性
  5. 	assert(p->num > 0);//断言存在有效数据
  6. 	p->num--;//尾删一个数据
  7. }

 

(2) 复杂度分析
  • 时间复杂度：没有变量影响时间，时间复杂度为O(1)。
  • 空间复杂度：没有变量影响空间，空间复杂度为O(1)。

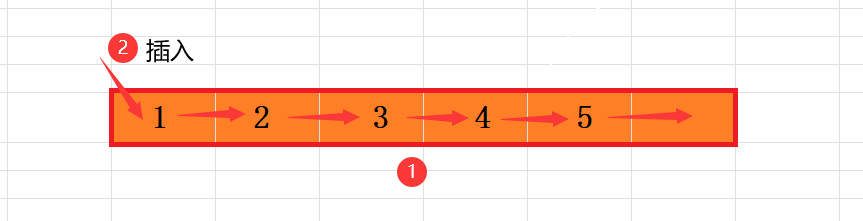
2.5 顺序表的头插

(1) 代码实现
  1. //5. 顺序表的头插
  2. void SeqListPushFront(SL* p, SLDataType x)
  3. {
  4. 	assert(p);//判断指针的有效性
  5. 	CheckSeqList(p);//先判断容量是否满了
  6. 	size_t end = p->num;
  7. 	while (end)
  8. 	{
  9. 		p->arr[end] = p->arr[end - 1];//整体向后移动
  10. 		end--;
  11. 	}
  12. 	p->arr[0] = x;//头插
  13. 	p->num++;//有效数据加一
  14. }

 

(2) 复杂度分析
  • 时间复杂度：因为从头部插入数据，后续数据需要依次覆盖，所以时间复杂度为O(N)。
  • 空间复杂度：因为可能会进行扩容，按最坏的情况来算，空间复杂度为O(N)。

2.6  顺序表的头删

(1) 代码实现
  1. //6. 顺序表的头删
  2. void SeqListPopFront(SL* p)
  3. {
  4. 	assert(p);//判断指针的有效性
  5. 	assert(p->num > 0);//有数据才删除
  6. 	size_t begin = 1;
  7. 	while (begin<p->num)
  8. 	{
  9. 		p->arr[begin - 1] = p->arr[begin];//整体向前移动
  10. 		begin++;
  11. 	}
  12. 	p->num--;// 有效数据减一
  13.  
  14. }

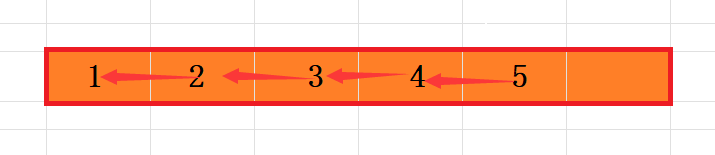 整体往前挪，把头覆盖~

(2) 复杂度分析
  • 时间复杂度：因为需要往前覆盖数据，所以时间复杂度自然为O(N)。
  • 空间复杂度：因为并没有开辟其他空间，所以空间复杂度为O(1)。

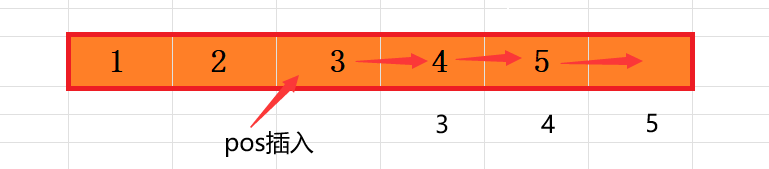
2.7 顺序表在pos位置插入

(1) 代码实现
  1. //7. 顺序表在pos位置插入
  2. void SeqListInsert(SL* p, size_t pos, SLDataType x)
  3. {
  4. 	assert(p);//判断指针的有效性
  5. 	assert(pos >= 0 && pos < p->num);//pos必须小于num并且大于等于0
  6. 	CheckSeqList(p);//判断容量是否满了
  7. 	for (int i = p->num; i >pos-1 ; i--)
  8. 	{
  9. 		p->arr[i] = p->arr[i - 1];//将pos后面的元素往后挪
  10. 	}
  11. 	p->arr[pos - 1] = x;//在pos位置加入数据
  12. 	p->num++;//有效个数加一
  13. }

 

(2) 复杂度分析
  • 时间复杂度：需要依次覆盖，时间复杂度为O(N)。
  • 空间复杂度：可能需要扩容，空间复杂度为O(N)。

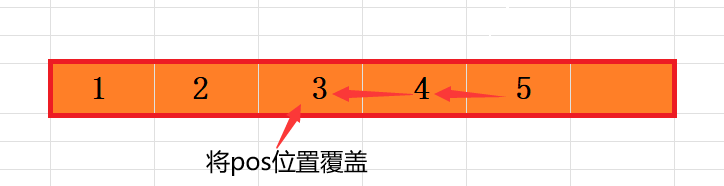
2.8  顺序表在pos位置删除

(1) 代码实现
  1. //8. 顺序表在pos位置删除
  2. void SeqListErase(SL* p, size_t pos)
  3. {
  4. 	assert(p);//判断指针的有效性
  5. 	assert(pos>=0&&pos<p->num );//pos必须小于num并且大于等于0
  6. 	assert(p->num > 0);//有数据才能删除
  7. 	for (int i = pos; i <p->num; i++)
  8. 	{
  9. 		p->arr[i-1] = p->arr[i];//将pos后面的元素往后挪
  10. 	}
  11. 	p->num--;//有效个数减一
  12. }

(2) 复杂度分析
  • 时间复杂度：需要依次覆盖，时间复杂度为O(N)。
  • 空间复杂度：没有额外的空间消耗，空间复杂度为O(1)。

2.9 顺序表的查找

(1) 代码实现

遍历数组查找~

  1. //9. 顺序表的查找
  2. int SeqListFind(SL* p, SLDataType x)//如果该数字存在则返回该数字的下标，否则返回-1
  3. {
  4. 	assert(p);//断言
  5. 	for (int i = 0; i < p->num; i++)
  6. 	{
  7. 		if (p->arr[i] == x)
  8. 		{
  9. 			return i;//查到返回下标
  10. 		}
  11. 	}
  12. 	return -1;//没有查到
  13. }

(2) 复杂度分析
  • 时间复杂度：以最坏的情况分析，时间复杂度为O(N)。
  • 空间复杂度：并没有格外的空间消耗，空间复杂度为O(1)。

2.10 顺序表的销毁

(1) 代码实现
  1. //10 顺序表的销毁
  2. void SeqListDestory(SL* p)
  3. {
  4. 	assert(p);//判断指针的有效性
  5. 	free(p->arr );//释放动态内存开辟的空间
  6. 	p->arr = NULL;
  7. 	p->capacity = 0;//容量置为0
  8. 	p->num = 0;//有效个数置为0
  9. }
(2) 复杂度分析
  • 时间复杂度：没有额外的时间消耗，时间复杂度为O(1)。
  • 空间复杂度：没有额外的空间消耗，空间复杂度为O(1)。

2.11 顺序表的打印

(1) 代码实现
  1. //11. 顺序表的打印
  2. void SeqListPrint(SL* p)
  3. {
  4. 	assert(p);//判断指针的有效性
  5. 	if (p->num == 0)
  6. 	{
  7. 		printf("顺序表为空！\n");
  8. 		return;
  9. 	}
  10. 	for (int i = 0; i < p->num; i++)
  11. 	{
  12. 		printf("%d ", p->arr[i]);//打印数据
  13. 	}
  14. 	printf("\n");
  15. }
(2) 复杂度分析
  • 时间复杂度：因为会打印顺序表中的所有数据，所以时间复杂度为O(N)。
  • 空间复杂度：打印顺序表并不需要开辟格外的空间，所以空间复杂度为O(1)。

 3. 完整代码

SeqList.c

  1. #define _CRT_SECURE_NO_WARNINGS
  2. #include"Test.h"
  3.  
  4.  
  5. //接口函数的实现
  6.  
  7. //1. 顺序表初始化
  8. void SeqListInit(SL* p)
  9. {
  10. 	assert(p);//判断指针的有效性
  11. 	p->arr = NULL;
  12. 	p->capacity = 0;
  13. 	p->num = 0;
  14. }
  15.  
  16. //2. 检查顺序表容量是否已满
  17. void CheckSeqList(SL* p)
  18. {
  19. 	assert(p);//判断指针的有效性
  20. 	if (p->num == p->capacity)
  21. 	{
  22. 		 size_t newcapacity=p->capacity == 0 ? p->capacity = 4 : p->capacity * 2;
  23. 		//如果原来没有空间，就给上4，有的话就扩大为原来的两倍
  24. 		 SLDataType* ptr = (SLDataType*)realloc(p->arr, newcapacity * sizeof(SLDataType));//动态扩容
  25. 		 if (ptr == NULL)
  26. 		 {
  27. 			 perror("realloc fail;");
  28. 			 return;
  29. 		 }
  30. 		 //也可以用assert断言一下
  31. 		 p->arr = ptr;//开辟成功将地址传给arr
  32. 		 p->capacity = newcapacity;//更新容量
  33. 	}
  34. }
  35.  
  36. //3. 顺序表的尾插
  37. void SeqListPushBack(SL* p, SLDataType x)
  38. {
  39. 	assert(p);//判断指针的有效性
  40. 	CheckSeqList(p);//尾插前先判断有没有容量或容量够不够
  41. 	p->arr[p->num] = x;//尾部插入数据
  42. 	p->num++;//有效数加一
  43. }
  44.  
  45. //4. 顺序表的尾删
  46. void SeqListPopBack(SL* p)
  47. {
  48. 	assert(p);//判断指针的有效性
  49. 	assert(p->num > 0);//断言存在有效数据
  50. 	p->num--;//尾删一个数据
  51. }
  52.  
  53. //5. 顺序表的头插
  54. void SeqListPushFront(SL* p, SLDataType x)
  55. {
  56. 	assert(p);//判断指针的有效性
  57. 	CheckSeqList(p);//先判断容量是否满了
  58. 	size_t end = p->num;
  59. 	while (end)
  60. 	{
  61. 		p->arr[end] = p->arr[end - 1];//整体向后移动
  62. 		end--;
  63. 	}
  64. 	p->arr[0] = x;//头插
  65. 	p->num++;//有效数据加一
  66. }
  67.  
  68. //6. 顺序表的头删
  69. void SeqListPopFront(SL* p)
  70. {
  71. 	assert(p);//判断指针的有效性
  72. 	assert(p->num > 0);//有数据才删除
  73. 	size_t begin = 1;
  74. 	while (begin<p->num)
  75. 	{
  76. 		p->arr[begin - 1] = p->arr[begin];//整体向前移动
  77. 		begin++;
  78. 	}
  79. 	p->num--;// 有效数据减一
  80.  
  81. }
  82.  
  83. //7. 顺序表在pos位置插入
  84. void SeqListInsert(SL* p, size_t pos, SLDataType x)
  85. {
  86. 	assert(p);//判断指针的有效性
  87. 	assert(pos >= 0 && pos < p->num);//pos必须小于num并且大于等于0
  88. 	CheckSeqList(p);//判断容量是否满了
  89. 	for (int i = p->num; i >pos-1 ; i--)
  90. 	{
  91. 		p->arr[i] = p->arr[i - 1];//将pos后面的元素往后挪
  92. 	}
  93. 	p->arr[pos - 1] = x;//在pos位置加入数据
  94. 	p->num++;//有效个数加一
  95. }
  96.  
  97. //8. 顺序表在pos位置删除
  98. void SeqListErase(SL* p, size_t pos)
  99. {
  100. 	assert(p);//判断指针的有效性
  101. 	assert(pos>=0&&pos<p->num );//pos必须小于num并且大于等于0
  102. 	assert(p->num > 0);//有数据才能删除
  103. 	for (int i = pos; i <p->num; i++)
  104. 	{
  105. 		p->arr[i-1] = p->arr[i];//将pos后面的元素往后挪
  106. 	}
  107. 	p->num--;//有效个数减一
  108. }
  109.  
  110. //9. 顺序表的查找
  111. int SeqListFind(SL* p, SLDataType x)//如果该数字存在则返回该数字的下标，否则返回-1
  112. {
  113. 	assert(p);//断言
  114. 	for (int i = 0; i < p->num; i++)
  115. 	{
  116. 		if (p->arr[i] == x)
  117. 		{
  118. 			return i;//查到返回下标
  119. 		}
  120. 	}
  121. 	return -1;//没有查到
  122. }
  123.  
  124. //10 顺序表的销毁
  125. void SeqListDestory(SL* p)
  126. {
  127. 	assert(p);//判断指针的有效性
  128. 	free(p->arr );//释放动态内存开辟的空间
  129. 	p->arr = NULL;
  130. 	p->capacity = 0;//容量置为0
  131. 	p->num = 0;//有效个数置为0
  132. }
  133.  
  134. //11. 顺序表的打印
  135. void SeqListPrint(SL* p)
  136. {
  137. 	assert(p);//判断指针的有效性
  138. 	if (p->num == 0)
  139. 	{
  140. 		printf("顺序表为空！\n");
  141. 		return;
  142. 	}
  143. 	for (int i = 0; i < p->num; i++)
  144. 	{
  145. 		printf("%d ", p->arr[i]);//打印数据
  146. 	}
  147. 	printf("\n");
  148. }

4. 完结散花

好了，这期的分享到这里就结束了~

如果这篇博客对你有帮助的话，可以用你们的小手指点一个免费的赞并收藏起来哟~

如果期待博主下期内容的话，可以点点关注，避免找不到我了呢~

我们下期不见不散~~

本文内容由网友自发贡献，转载请注明出处：https://www.wpsshop.cn/w/在线问答5/article/detail/812747
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号