- 1分组卷积/转置卷积/空洞卷积/反卷积/可变形卷积/深度可分离卷积/DW卷积/Ghost卷积/
- 22022年软件评测师_2022软件评测师 csdn
- 3全面的软件测试
- 4在 gitee 码云部署预览静态站点项目（国内站点）_gitee部署静态网站
- 513款趣味性不错(炫酷)的前端动画特效及源码(预览获取)分享（附源码）_炫酷的网页特效代码
- 6Android 同时打包debug版 release版_android buildconfig怎么打包debug
- 7香橙派AIpro初体验：搭建无线随身NAS
- 8Flutter 通过 VS code 连接 Android 模拟器（Windows）_vscode 安卓模拟器
- 9【协议】WebSocket协议总结_socket通信是全双工还是半双工
- 10搭建Elasticsearch、Kibana和Logstash环境：构建强大的数据分析平台
Fast-LIO论文阅读_fast lio算法是哪年的
赞
踩
一、系统流程与符号说明
1、定义流形中的＋－
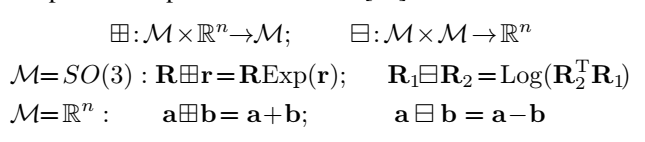
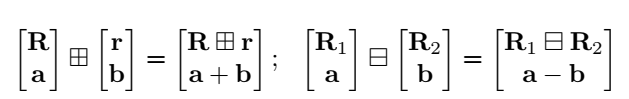
从上面的定义，很容易验证
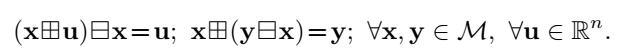
IEKF
| 符号 | 含义 |
|---|---|
| z j κ = G j ( G p ^ f j κ − G q j ) \mathbf{z}_{j}^{\kappa}=\mathbf{G}_{j}\left({ }^{G} \widehat{\mathbf{p}}_{f_{j}}^{\kappa}-{ }^{G} \mathbf{q}_{j}\right) zjκ=Gj(Gp fjκ−Gqj) | z j κ \mathbf{z}_{j}^{\kappa} zjκ LOAM的点到线、 点到面误差作为残差 |
| G() | 计算点到线、点到面残差的函数 |
| G q j { }^{G} \mathbf{q}_{j} Gqj | 真值 |
| x ^ \widehat{x} x | IMU积分的当前位姿 |
| P ^ k \widehat{\mathbf{P}}_{k} P k | IMU预积分的状态协方差 |
| P k {\mathbf{P}}_{k} Pk | 状态变量协方差 |
| L j n f j { }^{L_{j}} \mathbf{n}_{f_{j}} Ljnfj | 雷达测量噪声 |
| L j p f j g t = L j p f j − L j n f j { }^{L_{j}} \mathbf{p}_{f_{j}}^{\mathrm{gt}}={ }^{L_{j}} \mathbf{p}_{f_{j}}-{ }^{L_{j}} \mathbf{n}_{f_{j}} Ljpfjgt=Ljpfj−Ljnfj | 雷达真值 = 测量值 - 噪声 |
| T | 变换矩阵 |
观察方程：
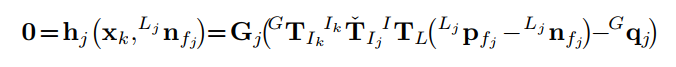
用它在
x
^
k
κ
\widehat{\mathbf{x}}_{k}^{\kappa}
x
kκ处的一阶近似来逼近上面的方程会得到
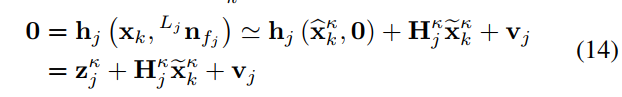
H
j
κ
\mathbf{H}_{j}^{\kappa}
Hjκ 是
h
j
(
)
h_j()
hj()关于
x
~
k
κ
\widetilde{\mathbf{x}}_{k}^{\kappa}
x
kκ的雅克比
v
j
v_j
vj 测量噪声，这里定义为了一个白噪声
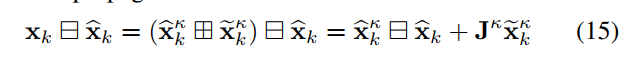
J
k
J^k
Jk是
(
x
^
k
κ
□
x
~
k
κ
)
□
x
^
k
\left(\widehat{\mathbf{x}}_{k}^{\kappa} \mathbb{\square{}} \widetilde{\mathbf{x}}_{k}^{\kappa}\right) \square \widehat{\mathbf{x}}_{k}
(x
kκ□x
kκ)□x
k 的雅克比
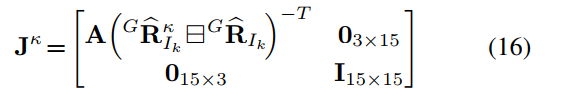
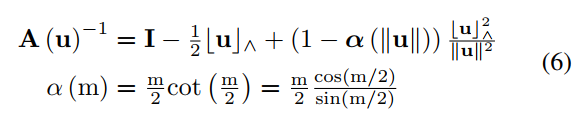
迭代初值为：
x
^
k
κ
=
x
^
k
\widehat{\mathbf{x}}_{k}^{\kappa}=\widehat{\mathbf{x}}_{k}
x
kκ=x
k, then
J
κ
=
I
\mathbf{J}^{\kappa}=\mathbf{I}
Jκ=I
将(15)中的先验与(14)中的后验分布相结合，得到最大后验估计(MAP)：
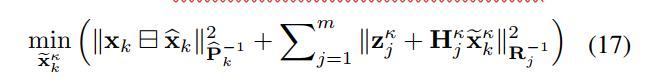
得到迭代卡尔曼公式
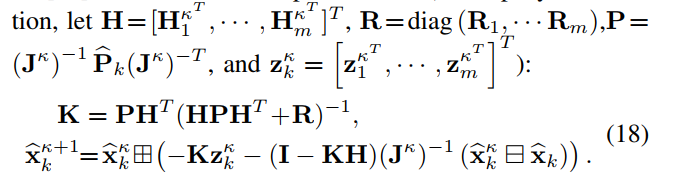注意： 这里的公式个人推出来好像不是（I-KH），而是（-KH）
R是雷达测量噪声矩阵
重复上面的步骤直至收敛,得到
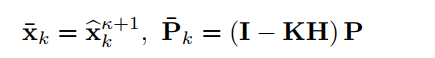
其中卡尔曼增益公式（18）可以用下面的公式替换，他们是等价的。这避免了对测量矩阵H求逆
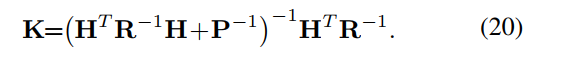
算法步骤
