yolov5源码解析(10)--损失计算与anchor_yolov5损失计算

本文章基于yolov5-6.2版本。主要讲解的是yolov5在训练过程中是怎么由推理结果和标签来进行损失计算的。损失函数往往可以作为调优的一个切入点，所以我们首先要了解它。

 一。代码入口

损失函数的调用点如下，在train.py里

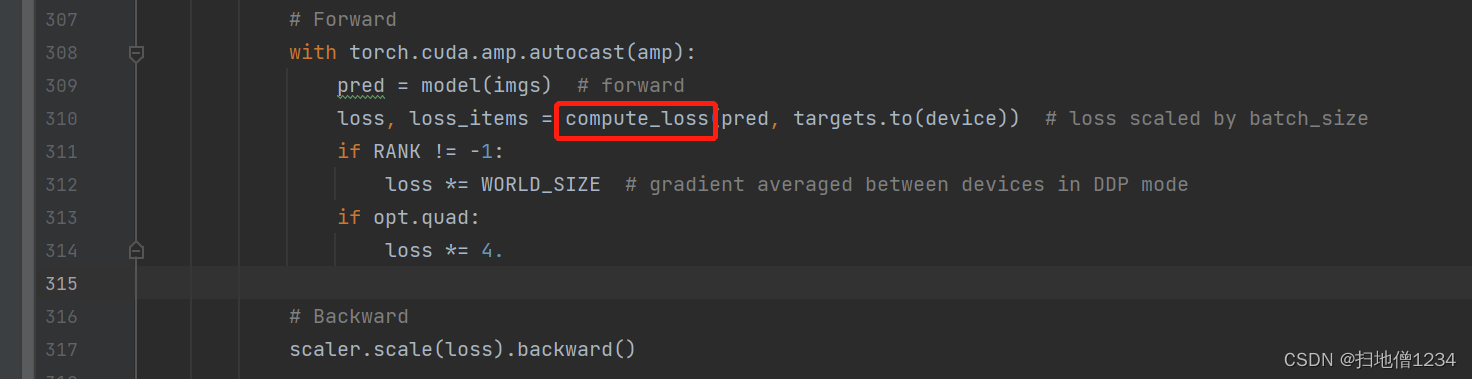
 代码入口：utils/loss.py

1.先说一下两个入参：

p: 推理结果列表，3个元素对应三个输出层，每层都是bs, na, ny, nx, no具体的输出可以参考上一篇博客

yolov5源码解析(9)--输出_扫地僧1234的博客-CSDN博客_yolov5三个输出

targets: 标签tensor，n行6列，每一行是image_index,class,x,y,w,h，image_index只是相对于当前的batch的index，比如batchsize选4，也就是4张图，那image_index就会有0，1，2，3

这里涉及到dataset和dataloader的相关代码，后面再补上具体的解析~~，不过先简单说两点

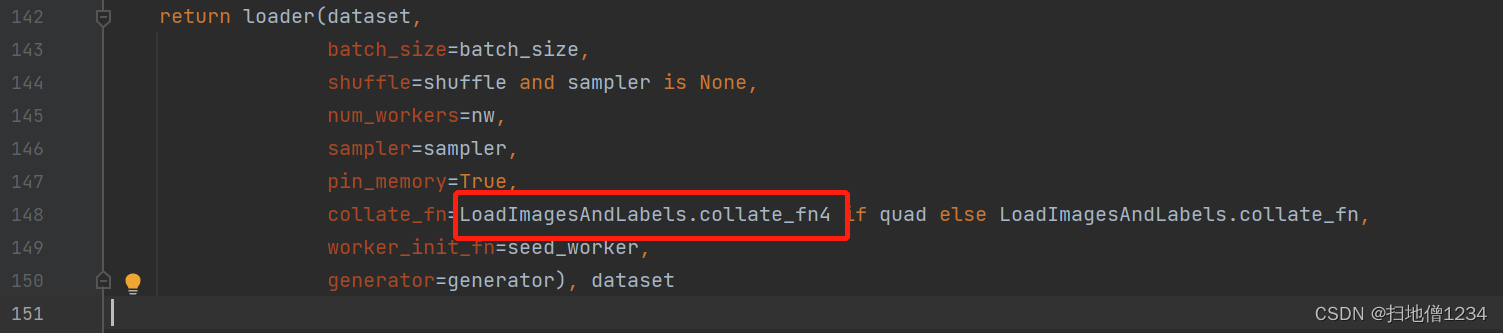
(1)dataset的代码在utils/dataloaders.py的LoadImagesAndLabels类里，主要是__getitem__函数，并且yolov5默认是会开启mosaic数据增强的，它会把当前的图和随机再选出的3张图合成一张图，那么对应的标签targets自然就是4张图的标签了，不过合成之后就是当成一张图来用，所以targets的image_index最终是同一个index。比如像下图。

(2)targets每行首位的image_index是在LoadImagesAndLabels.collate_fn4里面填上的，即是在dataloader层面完成的。

二。计算方法

先简单讲一下损失函数的计算逻辑

 损失函数分三部分:

(1)分类损失Lcls

(2)置信度损失Lobj

(3)边框损失Lloc

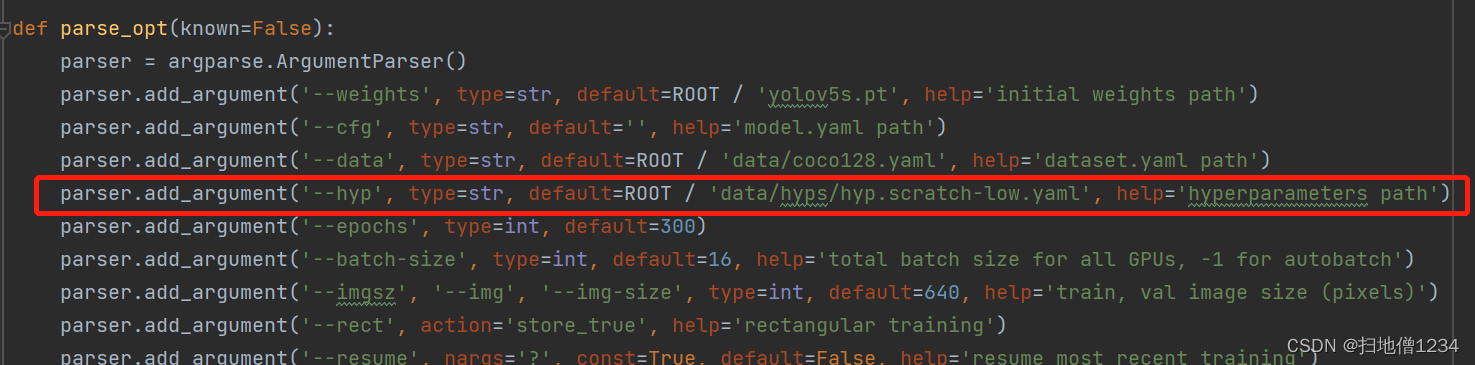
这三者的权重都是可以设置的，在data/hyps/hyp.scratch-low.yaml中，如下图

 注：默认用的超参数的配置文件就是data/hyps/hyp.scratch-low.yaml，如果你想改成别的文件的话可以自己在训练命令行中指定--hyp参数

1.分类损失

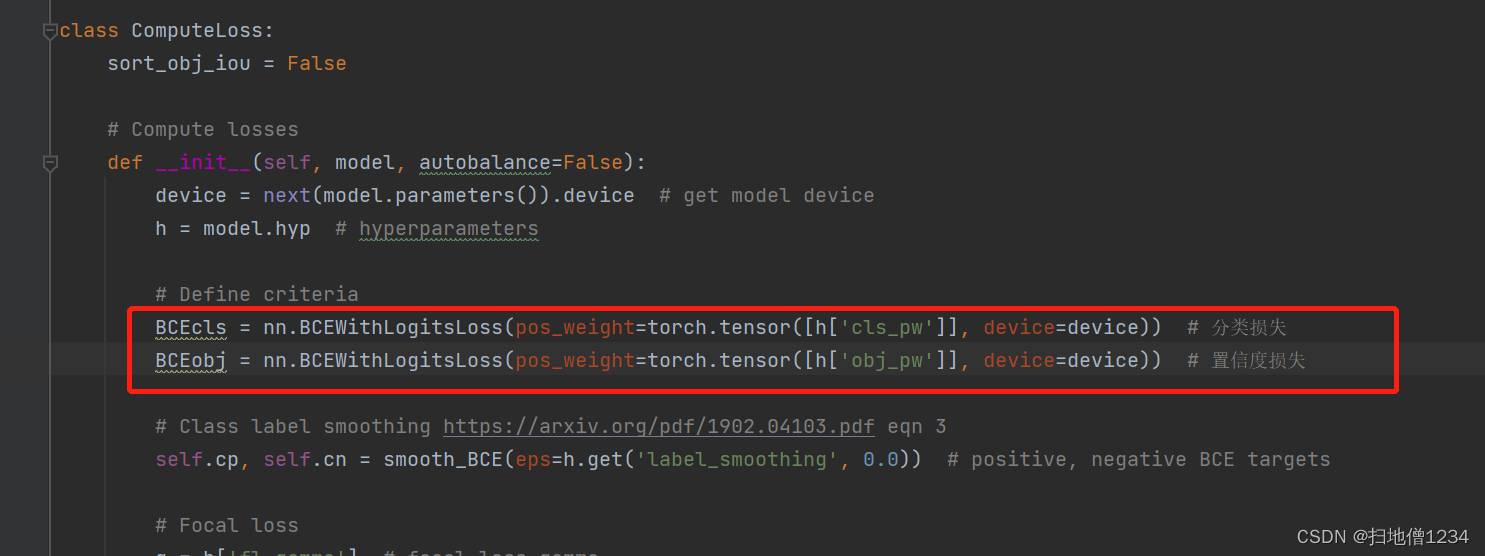
采用nn.BCEWithLogitsLoss，即二分类损失，你没听错，就是用的二分类损失，比如现在有4个分类：猫、狗、猪、鸡，当前标签真值为猪，那么计算损失的时候，targets就是[0, 0, 1, 0]，推理结果的分类部分（推理结果即输出的格式，具体可以上一篇博客

yolov5源码解析(9)--输出_扫地僧1234的博客-CSDN博客）也会有4个值，分别是4个分类的概率，就相当于计算4次二分类损失，取均值，从原理上来说自然也是可以的。并且还有如下原因：

(1)还可以计算多标签分类损失

(2)后面讲到的置信度损失也是用的BCEWithLogitsLoss，这两者都用同一种损失更容易进行平衡

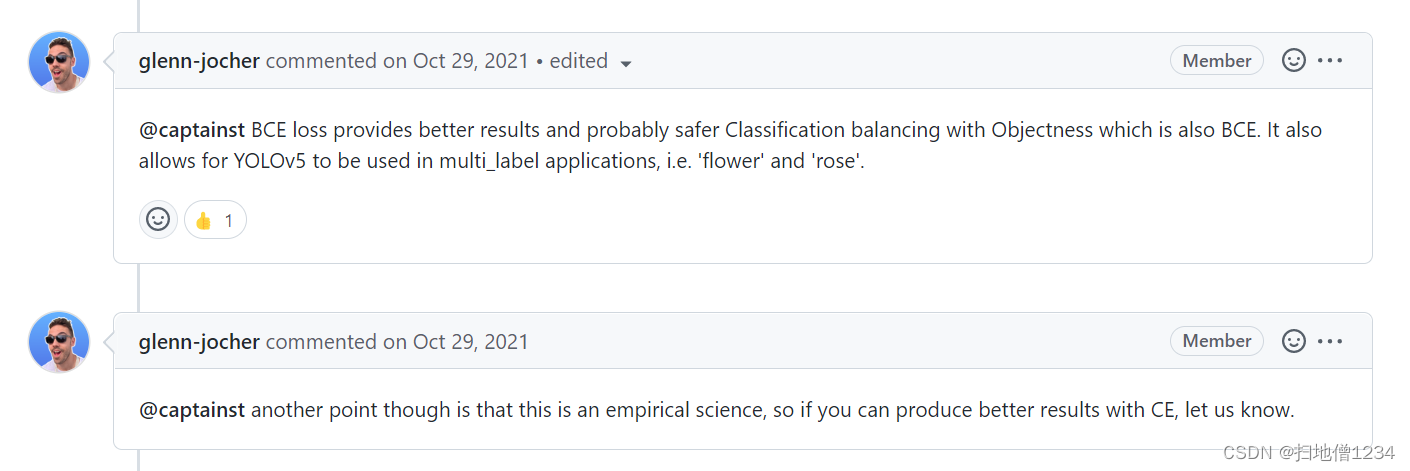
(3)用BCE就是得到了更好的效果，如果大家能证实CrossEntropy的效果更好，是可以去联系yolov5的作者的哦

以下贴出作者的答复

https://github.com/ultralytics/yolov5/issues/5401

这边要提到一个有意思的东西，就是yolov5里面的各种参数值，各种网络结构（比如C3），都不是作者凭空想象拍脑袋定的，都是基于经验、实验效果来定的，当然也不排除会有一些能改进的地方，比如Focus层就被改掉了~~

还三点要补充：

(1)按照640乘640分辨率，3个输出层来算的话，P3是80乘80个格子，P4是40乘40，P5是20乘20，一共有8400个格子，并不是每一个格子上的输出都要去做分类损失计算的，只有负责预测对应物体的格子才需要做分类损失计算（边框损失计算也是一样）。至于哪些格子才会负责去预测对应的物体，这个逻辑下面再说。

(2)分类的真值也不一定是0或1，还可以作label smoothing，感兴趣的话可以看一下相关代码和论文

 这个label smoothing是在命令行参数里指定的，默认是0，就是没使用。

(3)分类损失的权重（超参数hyp['cls']）在train.py里会做相应的修正

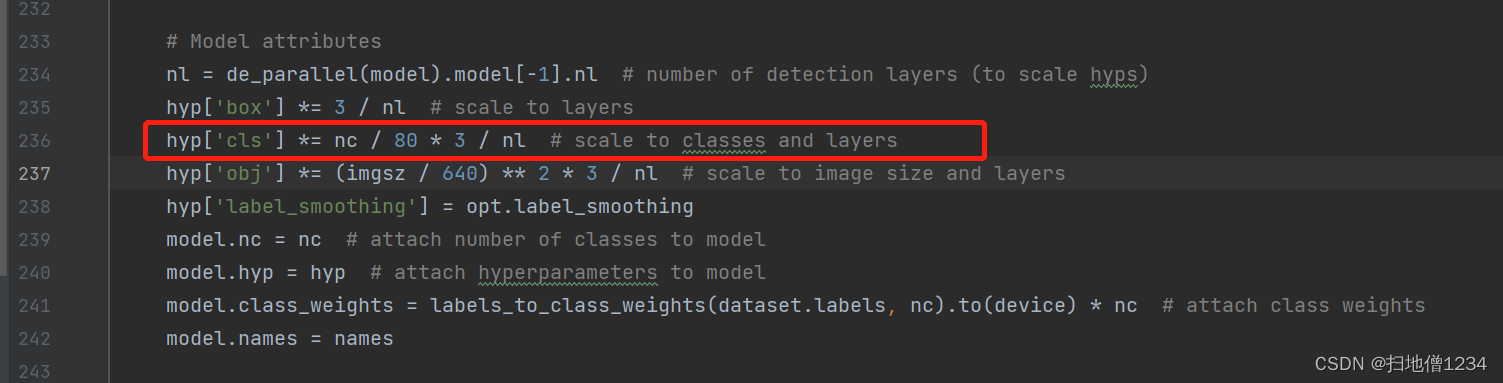
 首先box,cls,obj三个参数都会乘以一个3/nl，nl就是输出层数，默认是3层，3层的损失是相加的。所以如果改为5层，那损失自然要按比例修正一下。

然后cls还会乘以nc/80，nc就是分类数，80是coco数据集的80个分类，如果自己的数据集只有4个分类，那就会乘以4/80。为啥要这样呢？可能是为了平衡各个输出，BCEWithLogitsLoss默认用的计算策略是'mean'，即求均值，也就是说80个分类，对应了80个通道的输出，计算损失时是求均值。而4个分类，计算损失也求均值。那这两个值其实会差不多。但是80个通道的值与4个通道的值在损失中应当占有的比例应该是不一样的，应该成正比（有可能这跟采用BCE损失相关）。所以如果变成4通道，那就应该减小它的权重。----只是个人猜测啊，暂时先不去求证了，留坑留坑~~

 2.置信度损失

上面已经说了，也是BCEWithLogitsLoss，不过置信度是每一个格子都要做损失计算的，因为最终在使用的时候我们首先就是由置信度阈值来判断对应格子的输出是不是可信的。置信度的真值并不是固定的，如果该格子负责预测对应的物体，那么置信度真值就是预测边框与标签边框的IOU。如果不负责预测任何物体，那真值就是0(不过看代码的话里面还有一个gr参数，然后作者说这个是GIOU的一个rate值，但我暂时并没有找到哪儿能改这个值，这个值初始值就是1，暂时先留个坑)

 另外还要补充一下的是BCEWithLogitsLoss有一个pos_weight参数

 默认都是1.0（好，相关超参数集齐了）

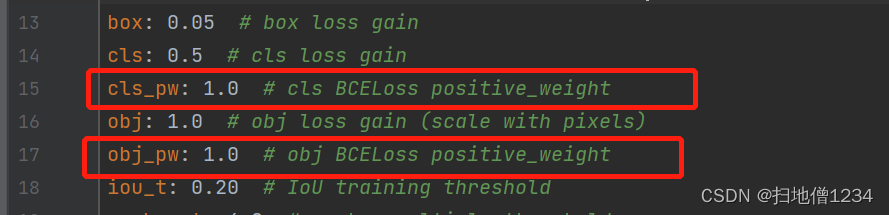
 如果pos_weight就是1的话，那相关公式就是下面这样的（图取自pytorch官方文档）

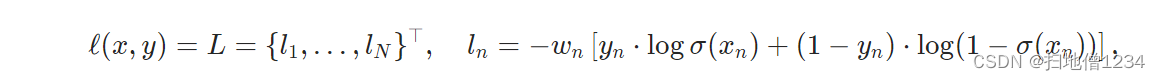
 而如果不是1呢，它是用来平衡正负样本损失的，如下，就是pc，这边的c指的是不同的分类，对于置信度来说就相当于1个分类了，从如下公式可以看出，如果标签为正样本，即ync=1，那这个pc才有效，否则是负样本，算的是后半部分值。

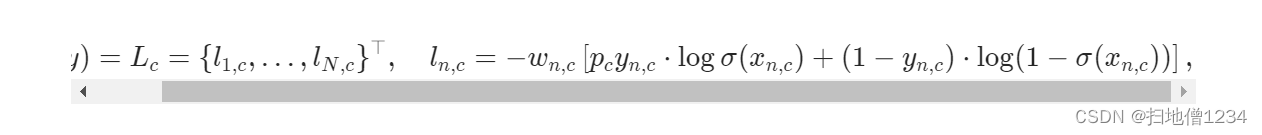
所以如果我们想提高recall召回率，即正样本如果推理成负样本，那损失要大一些，那么就可以提高pos_weight的值，但这样就会降低精度，因为模型更倾向于推理出更多的正样本（尽管可能会提升FP false positive的值）。所以如果相反，要提升精度，自然是降低pos_weight的值。

但是如果正负样本本身就不平衡，比如正样本100个，负样本300个，如果要平衡正负样本，那pos_weight就应该设置为3。

不过这边有一个问题了，之前说了三层一共会有8400个格子啊，而实际上负责预测对应的物体的格子只占一小部分，甚至一小小部分，正负样本不平衡啊，为啥这个pos_weight仍然是1呢？

这个问题需要从几方面入手：

(1)首先作者做过实验，他发现与其提升pos_weight，不如直接提升置信度整体的权重效果更好，如果提升pos_weight，那可能会导致提升FP，出现更多的假正例。

可以看看这个问题（虽然它其实问的是另一个问题~~） 

Why Objectness Loss is Scaled with Image Size? · Issue #6192 · ultralytics/yolov5 · GitHub

 

也就是说有可能这里的负样本过多导致的问题是总体损失过小，所以我们直接提升总体损失就行了。

(2)上面说了，不如直接提升置信度整体的权重，不过这个整体指的并不是三个输出层提升一样的权重哦，P3(80x80)，P4(40x40)，P5(20x20)，那么一般来说，肯定是P3里面会有更多的格子是负样本啊（具体哪些格子负责预测物体的逻辑再等等，下面说~~），也就是说P3的正负样本最不平衡，P4次之，P5的不平衡情况最不严重。所以如果按(1)里面的逻辑，P3的置信度损失提升的应该最多，P4次之，P5最少。事实上确实是这样的，如下图

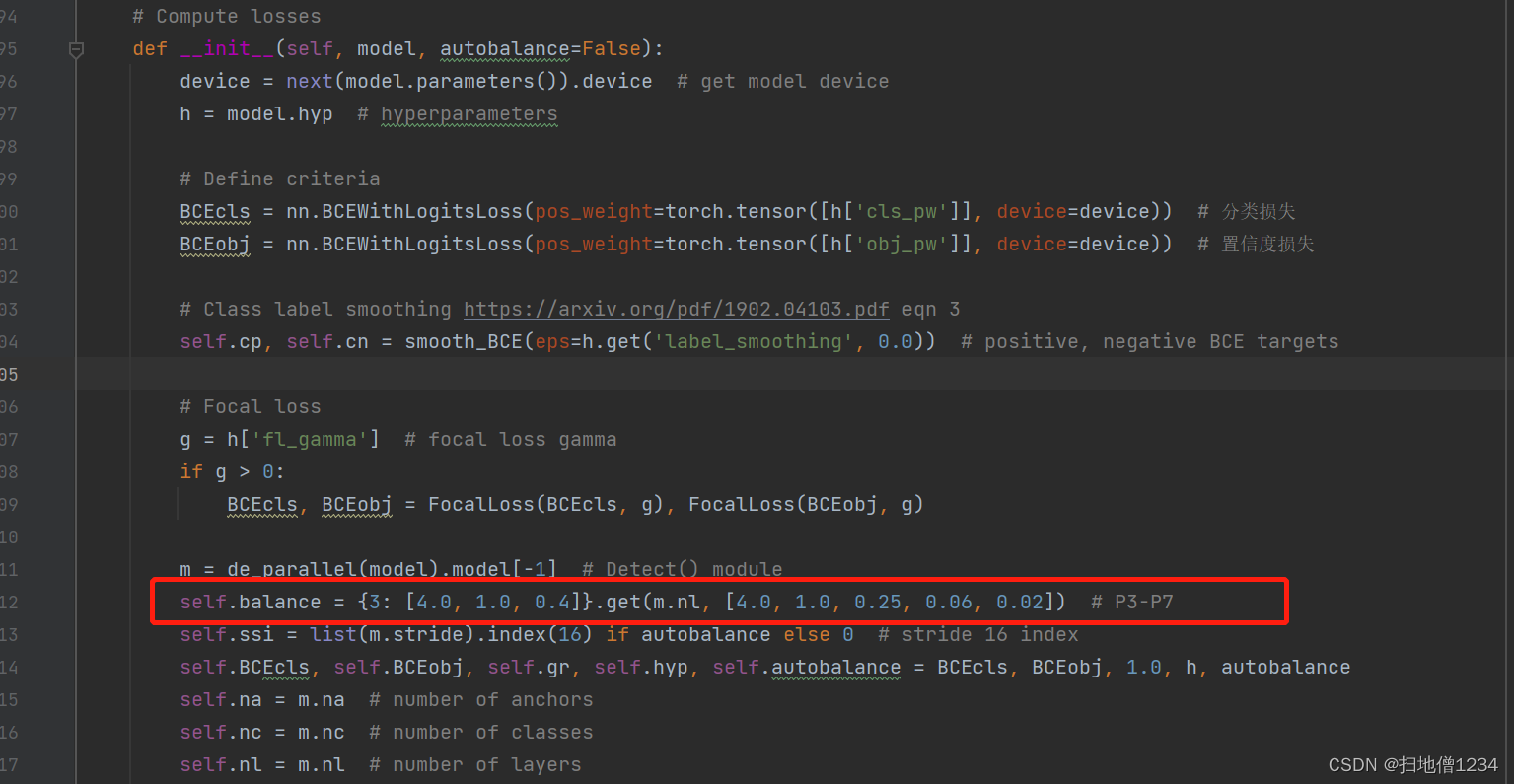
 这边不同层的置信度损失会乘以不同的比例，P3乘4，P4乘1，P5乘0.4，此外如果是5个输出层，那自然会有5个系数了。

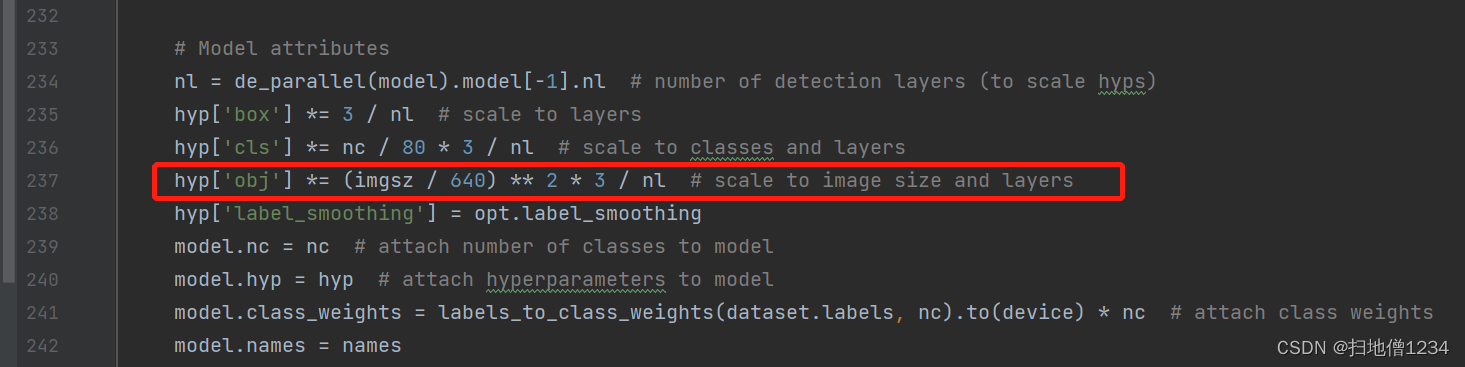
 (3)格子越多，负样本就会越多（一般情况），那还有一个问题，训练图片大小是可以改的，默认是640乘640，如果我们把它改大了，或者改小了，都会导致格子数就不一样了，那还用跟原来一样的权重，是不是就不适合了呢？在train.py里面已经有解决办法了，会根据图片尺寸的平方来修正的，如下（尺寸的平方就是面积啦，跟格子数是成正比的）。

(4)默认是开启mosaic数据增强的，会把4张图拼起来，所以有可能正样本会更多一些，比如最多的情况，按照默认的scale0.5来算，假设正好随机到缩放到0.5(随机范围是0.5-1.5)，然后4张图拼接的中心点正好在图片中央，此时4张图就会拼成完整的一张图并缩放到640乘640的大小，所有的正样本都保留下来啦，此时正样本就是最多的。

 3.边框损失

边框损失由预测边框与标签边框的IOU来定，IOU越大，损失自然越小，IOU如果是1，损失就是0，IOU如果是0，损失就越大，上限定为1，所以边框损失就是1-IOU

 需要说明的几点是：

(1)这里的IOU并不是简单的IOU，而是CIoU，这里就不具体展开讲了，可以看看其它的帖子

(2)预测边框的几个值的计算方法具体见上一篇博客

(3)只有负责预测对应物品的格子上的输出才会计算IOU损失

4.到底哪些格子负责预测物体？

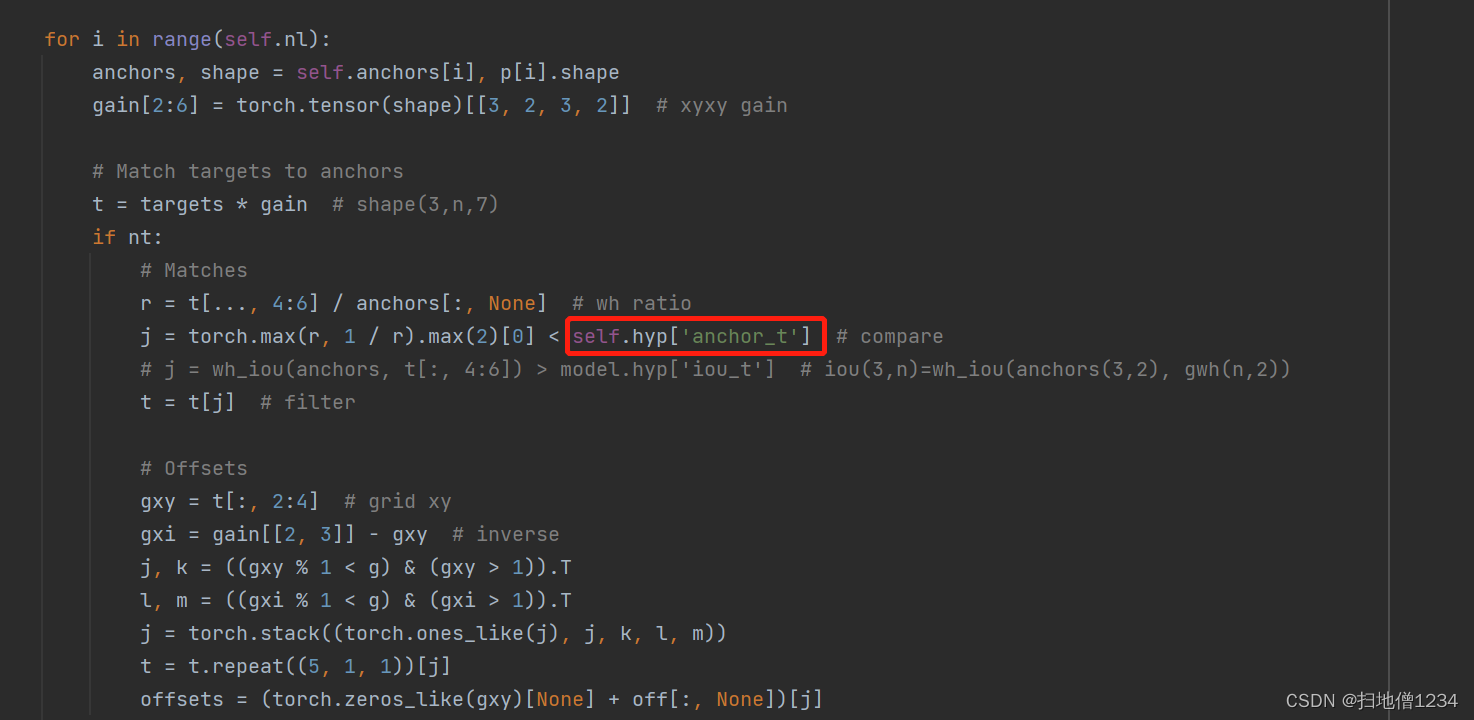
(1)anchor匹配

上一篇博客中就讲到了，每个输出层会有3个anchor，每个anchor的宽高不一

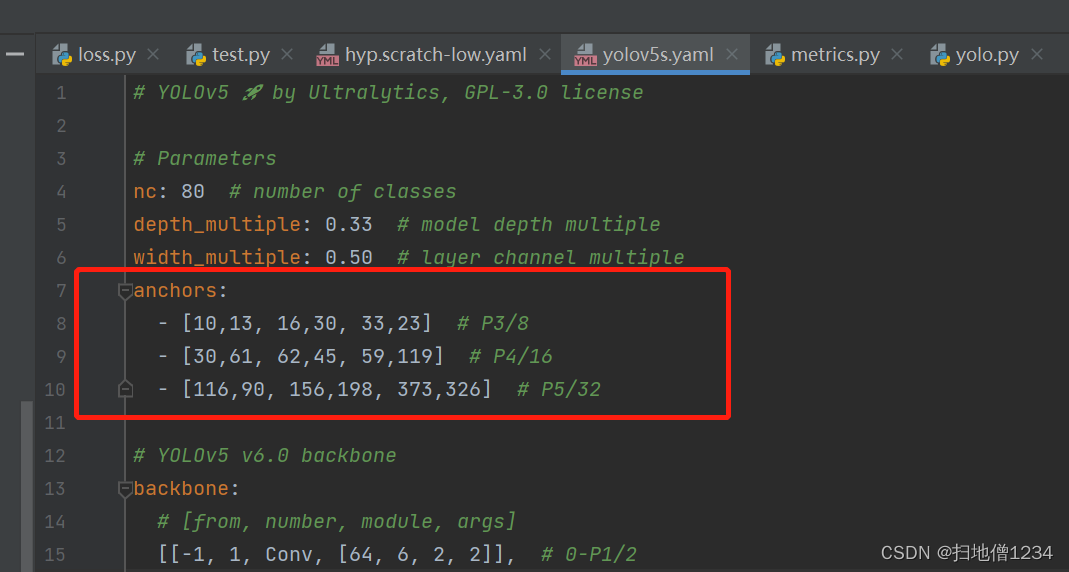
预测边框的宽高是基于anchor来预测的，而预测的比例值是有范围的，即0-4，如果标签的真实宽高与anchor的宽高的比例超过了4，那是不可能预测成功的，所以哪些anchor能匹配上哪些标签，就看anchor的宽(高)与标签的宽(高)的比例有没有超过4，如果超过了，那就不匹配。注意，这个比例是双向的比例，比如标签宽/anchor宽>4，不匹配，而anchor宽/标签宽>4，也是不匹配的，其实也很有道理啊

a)不然大anchor不就一篮子全包了吗~~

b)如果anchor比标签大很多还需要匹配的话，可能出现在P5层去预测小物体，而P5层的小物体特征不明显，本来就不适合预测小物体

c)如果真要预测，那预测值就接近0，对应的sigmoid区间的梯度也接近0了，不容易收敛

直接上官方文档的图了。

补充一下，比例阈值4是个超参数，可以调整的。

 (2)格子匹配

首先对应输出层至少要有一个anchor能匹配到对应物体，否则的话这个输出层就不会负责预测这个物体了。接下来才是找格子，逻辑很简单

a)标签边框（真实物体边框）的中心点落在哪个格子上，就由这个格子负责预测该物体

b)然后还会取这个格子的两个邻居格子来预测该物体，如果标签边框的中心点在格子的左上位置，那就由格子的左邻居，上邻居预测该物体。

右上位置，就由格子的右邻居，上邻居预测该物体。

左下位置，就是左邻居，下邻居。

右下位置，就是右邻居，下邻居。

正正好中间？那就只有这个格子，不过一般不可能正正好了。

恕我有点懒，继续搬官方的图

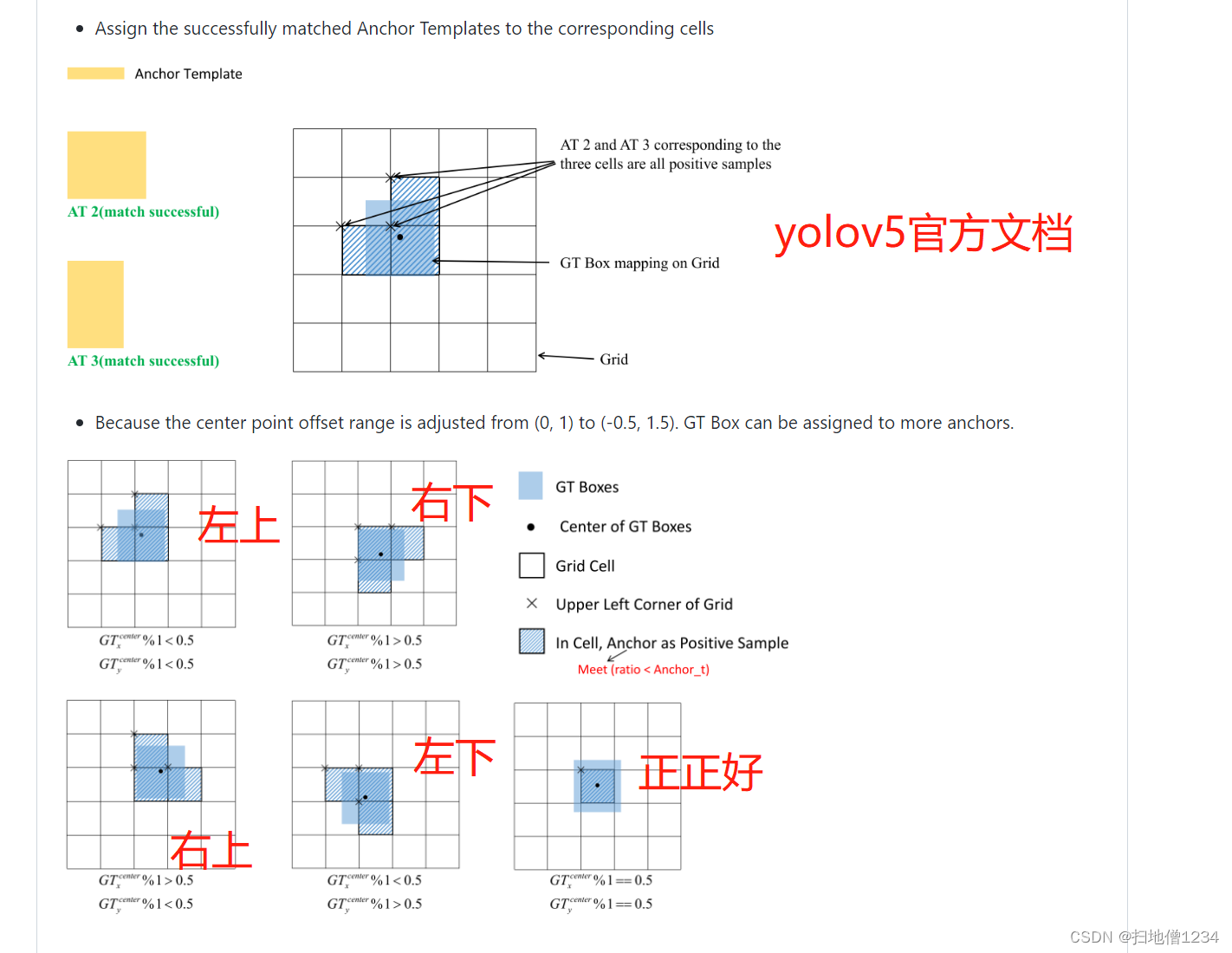
这边的解释有：

a)中心点的输出经过计算，其范围可以是-0.5-1.5（具体可见上一篇博客），自然就可以归到旁边的格子里了

b)之前不是说有正负样本不平衡的问题吗，这一下加了两个邻居进来，正样本瞬间多了两倍，岂不是利于平衡 --------这是有人的帖子里说的，好像也有点道理

c)旁边的格子里其实本来就可能有这个物体的特征，只是不太正而已，因为大家的视野都是很大的麻，所以预测一下也是可以的，并且只加两邻居说不定还算少呢。

(3)再结合(1)(2)两点分析一下

a)一个物体在某个输出层上可能由几个格子预测呢，一般来说3个，也可能是1个（正正好），还有一种情况也1个，就是下面这样

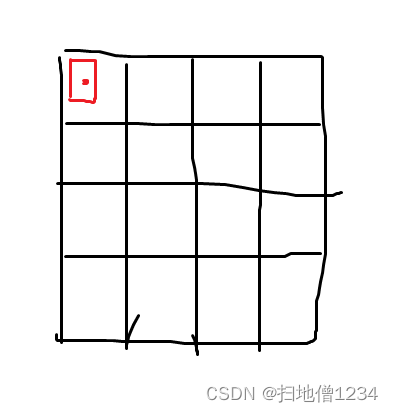
 所以也会有两个的情况，就是这样

这么小的物体能匹配上anchor吗？能啊，就拿P5来说，20x20的格子，640分辨率，一个格子是32分辨率， 最小的anchor是116,90，除以4的话都比32小，所以小于一个格子的物体是可以匹配上的。

b)那一个格子上最多几个anchor能匹配上物体呢，肯定是3个啦，比例阈值4其实还是很宽的，所以同一个格子上的3个anchor都匹配到同一个物体，完全可以。

所以一个输出层上最多会有3个格子乘3个anchor，即9项输出匹配一个物体

c)那如果一个格子同时满足匹配两个物体，并且一个anchor同时满足匹配两个物体，会咋样？

那这个格子的这个anchor就会既要匹配物体A，又要匹配物体B，算两次损失（分类损失与边框损失）----------这不是有点奇怪吗？就是有点奇怪，并且这还有可能导致一些奇怪的现象，后面会用一个训练的实例来说明这个问题。

下面先证实一下逻辑c到底是不是真的。

搞了一个数据集，里面就一张图，两个分类，pad:平板，earplug：耳塞

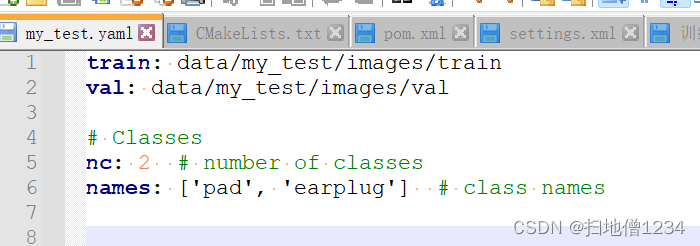
 耳塞基本在平板的中间，这样它们的中心点就能归到同一个格子上

 为了方便测试验证，把缩放和mosaic数据增强都关了，也就是说实际训练的图就是原图（自然是缩放到640乘640啦）

 调试的时候关键是看这两个值

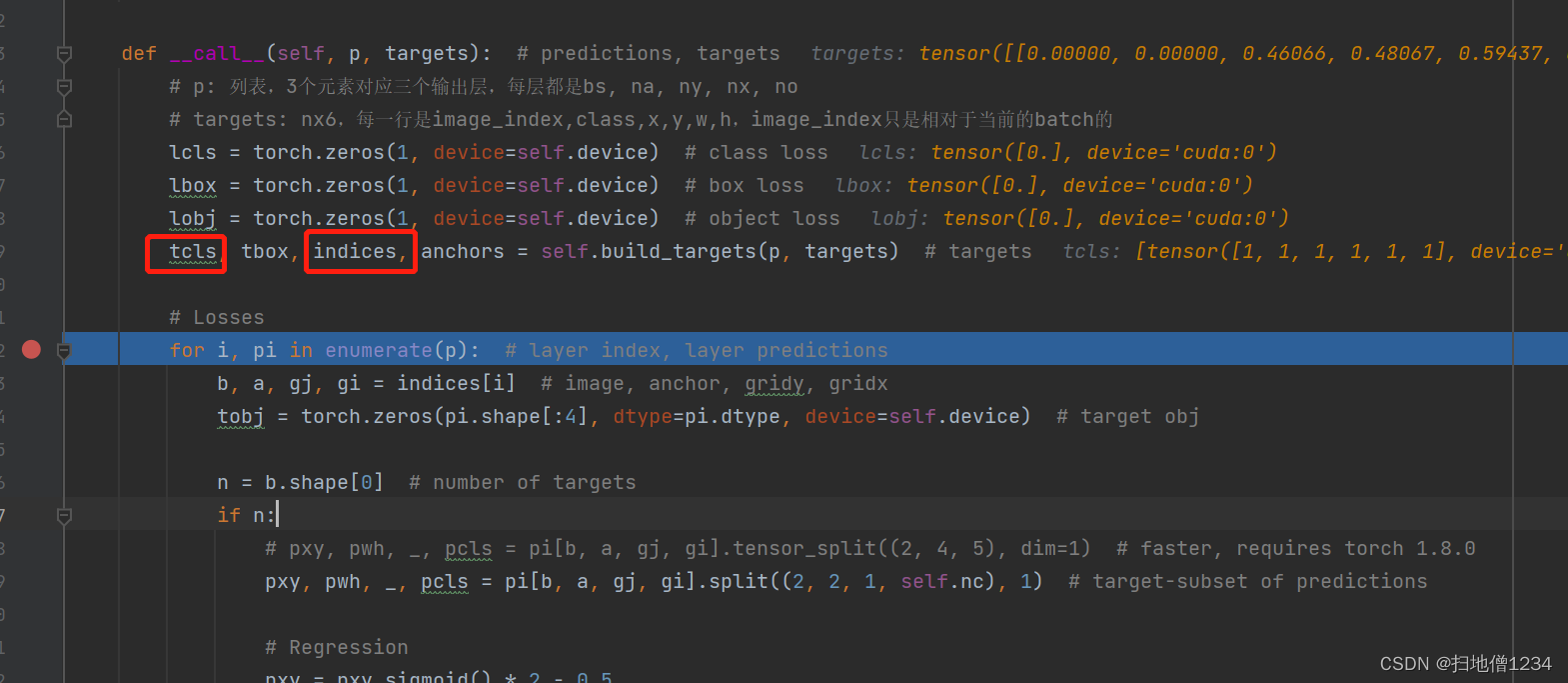
先上图

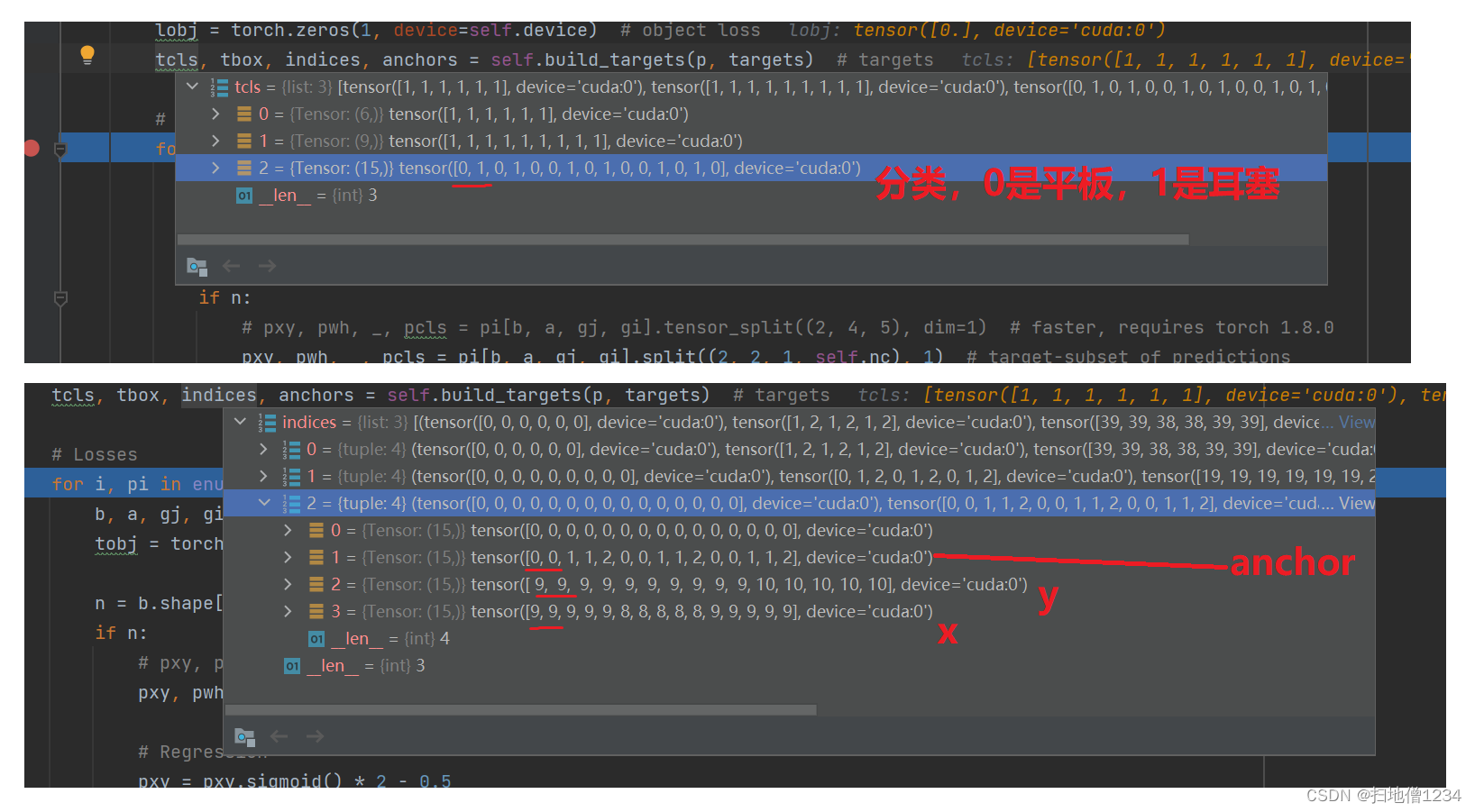
 直接就看头两项，都是在第3个输出层，第一个匹配上的就是0平板，anchor索引0即116,90这一个anchor，第(9,9)个格子，第二个匹配上的是1耳塞，其它信息一样。

所以说第3个输出层的第(9,9)个格子的第1个anchor既匹配平板，也匹配耳塞。

5.源码详解

先上标签匹配anchor这一部分的源码解析

    def build_targets(self, p, targets):
        # Build targets for compute_loss(), input targets(image,class,x,y,w,h)
        # na即每一层的anchor数，一般就是3了
        # nt就是标签数，注意默认是开启mosaic数据增强的，所以是4张图的标签数，并且有可能由于截取了图像，有些标签会被去掉。
        na, nt = self.na, targets.shape[0]  # number of anchors, targets
        tcls, tbox, indices, anch = [], [], [], []
        gain = torch.ones(7, device=self.device)  # normalized to gridspace gain
        """
        假设nt是2，两个标签，则ai就是:
        0 0
        1 1
        2 2
        """
        ai = torch.arange(na, device=self.device).float().view(na, 1).repeat(1, nt)  # same as .repeat_interleave(nt)
        # 标签重复3次，就变成了(3, 2, 6)，ai是(3, 2)，后面加个None就变成(3, 2, 1)，就可以自动广播拼接啦
        # 简言之，就是先默认每个标签都能匹配上3个anchor，所以把标签重复3次，标签新增一列：匹配的anchor索引
        targets = torch.cat((targets.repeat(na, 1, 1), ai[..., None]), 2)  # append anchor indices
 
        g = 0.5  # bias
        off = torch.tensor(
            [
                [0, 0],
                [1, 0],
                [0, 1],
                [-1, 0],
                [0, -1],  # j,k,l,m
                # [1, 1], [1, -1], [-1, 1], [-1, -1],  # jk,jm,lk,lm
            ],
            device=self.device).float() * g  # offsets
 
        for i in range(self.nl):  # 分别处理3个输出层
            # 3个anchor，3行2列
            anchors, shape = self.anchors[i], p[i].shape
            gain[2:6] = torch.tensor(shape)[[3, 2, 3, 2]]  # xyxy gain
 
            # Match targets to anchors
            t = targets * gain  # shape(3,n,7) 把标签里的x,y,w,h相对值乘上输出特征图宽高，变成绝对值
            if nt:
                # Matches, 所有标签的宽高，注意t的shape是(na, nt, 7)，t[..., 4:6]就是(na, nt, 2)，anchors是(na, 2)，
                # 所以anchors是在中间加一个维度变成(na, 1, 2)，然后才能自动广播
                # 之前我们不是默认每个标签都能匹配上3个anchor吗，现在得筛选一下，把每个标签的宽高都除以对应的anchor宽高，其比值或比值的倒数
                # 都必须小于anchor_t(默认4)，否则丢弃此项匹配，简言之就是你不能比anchor大很多，也不能比它小很多
                r = t[..., 4:6] / anchors[:, None]  # wh ratio
                j = torch.max(r, 1 / r).max(2)[0] < self.hyp['anchor_t']  # compare，为何后面还有个[0]，因为max返回的是max值和索引
                # j = wh_iou(anchors, t[:, 4:6]) > model.hyp['iou_t']  # iou(3,n)=wh_iou(anchors(3,2), gwh(n,2))
                t = t[j]  # filter，这里就是在过滤掉不符合的匹配项，注意过滤之后，t的shape就变成(n, 7)了
 
 
                # 这段逻辑还是先看博客里的“4.到底哪些格子负责预测物体？”然后再看代码比较好理解
                # Offsets
                gxy = t[:, 2:4]  # grid xy，标签中心点坐标
                gxi = gain[[2, 3]] - gxy  # inverse，反过来的中心点坐标，
                j, k = ((gxy % 1 < g) & (gxy > 1)).T  # 哪些标签的中心点处于格子左半边或上半边，注意这里的.T，不转置是分不开的
                l, m = ((gxi % 1 < g) & (gxi > 1)).T  # 哪些标签的中心点处于格子右半边或下半边
                j = torch.stack((torch.ones_like(j), j, k, l, m))
                # 如果中心点在格子左半边，则左边的邻居格子也负责预测该标签，上半边则上边的邻居格子也负责预测，右半边、下半边同理，
                # 既然负责预测，那我们的标签自然又得多复制一份了。这里是先重复5份，然后由上面的规则进行筛选
                # 一般来说左半右半二选一，上半下半二选一，所以基本上最终会重复3次。不过也有特殊情况，比如正正好在中间，或者处于图像边缘
                t = t.repeat((5, 1, 1))[j]
                # 后面会用标签的中心点坐标减去这个偏移，再取整，从而得到每个标签对应的预测格子，
                # 所以如果是要移到左边的邻居格子，肯定是x减0.5，上边就是y减0.5，下边就是y减-0.5，右边就是x减-0.5，中间自然是减0
                # gxy是(n, 2)变成(1, n, 2), off是(5, 2)变成(5, 1, 2)，就可以广播啦，然后通过j进行过滤
                offsets = (torch.zeros_like(gxy)[None] + off[:, None])[j]
            else:
                t = targets[0]
                offsets = 0
 
            # Define
            bc, gxy, gwh, a = t.chunk(4, 1)  # (image, class), grid xy, grid wh, anchors
            a, (b, c) = a.long().view(-1), bc.long().T  # anchors, image, class
            gij = (gxy - offsets).long()  # 减完偏移，取个整，就得到对应的预测格子的索引，或者说是格子左上角的坐标
            gi, gj = gij.T  # grid indices
 
            # Append
            # 后面就可以用这个索引从模型的推理结果中取出需要匹配标签的那一部分
            indices.append((b, a, gj.clamp_(0, shape[2] - 1), gi.clamp_(0, shape[3] - 1)))  # image, anchor, grid
            tbox.append(torch.cat((gxy - gij, gwh), 1))  # box，中心点坐标最终取的是相对于格子左上角的值，跟推理值相一致
            anch.append(anchors[a])  # anchors
            tcls.append(c)  # class
 
        return tcls, tbox, indices, anch