[论文笔记]BM25S：Python打造超越RANK-BM25的实现

引言

今天带来一篇BM25变种的论文笔记，不要低估BM25，在RAG中检索中通常都会引入BM25检索，然后配合嵌入模型进行混合检索。

BM25S: Orders of magnitude faster lexical search via eager sparse scoring，题目翻译过来是： 通过快速稀疏评分实现数量级速度提升的词汇检索。

BM25S是一种高效的基于Python的BM25实现，仅依赖于Numpy和Scipy。与最流行的基于Python的框架(Rank-BM25)相比，BM25S在索引期间通过即时(eager)计算BM25分数并将其存储到稀疏矩阵中，实现了高达500倍的速度提升。

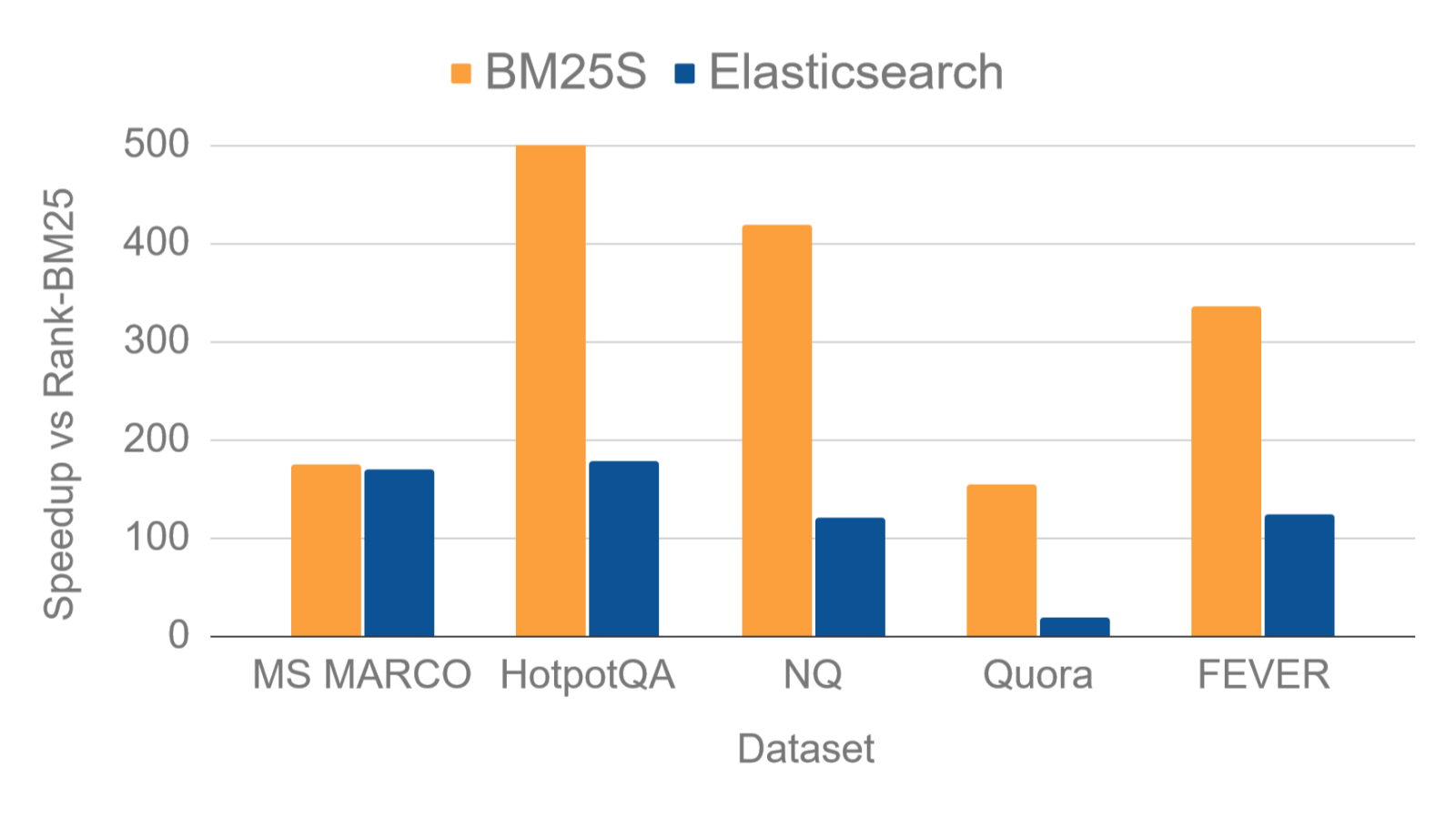
代码开源在：https://github.com/xhluca/bm25s

1. 背景

稀疏词汇搜索算法(Sparse lexical search algorithms)，比如BM25，仍然得到了广泛地应用，因为不需要训练，可应用于多种语言，并且速度较快。尤其是基于Lucene的实现，通常比现有的基于Python的实现(如Rank-BM25)更快。

本篇工作通过引入两项改进，能带来比现有基于Python实现显著的速度提升：在索引语料库时即时计算所有可能分配给任何未来查询标记的分数，并将这些计算存储在稀疏矩阵中，以便实现更快速的切片和求和。稀疏矩阵的思想在BM25-PT中被探索，它使用PyTorch预计算BM25分数，并通过稀疏矩阵乘法将其与查询的词袋编码相乘。

而本篇工作的BM25S不依赖于Pytorch，使用Scipy的稀疏矩阵实现，BM25-PT通过词袋与文档矩阵相乘，而BM25S则切片相关索引并在标记维度上进行求和，消除了矩阵乘法的需求。实现时BM25S还引入了一种简单快速的基于Python的分词器。

2. 实现

BM25的计算 我们使用Lucene提出的评分方法，对于一个给定查询$Q$(分词为$q_1,\cdots ,q_{|Q|})$和来自集合$C$中的文档$D$，计算下面的分数：
$$\begin{array}{rl}B(Q,D)& =\sum _{i=1}^{|Q|}S(q_i,D)\\ & =\sum _{i=1}^{|Q|}\text{IDF}(q_i,C)\frac{\text{TF}(q_i,D)}{\mathcal{D}}\end{array}$$
其中$\mathcal{D}=\text{TF}(t,D)+k_1\left(1-b+b\frac{|D|}{L_{\text{avg}}}\right)$，$L_{\text{avg}}$是语料库$C$中的平均文档长度(通过标记数计算)，$\text{TF}(q_i,D)$是标记$q_i$在文档$D$中的词频，$\text{IDF}$是逆文档频率，计算为：
$$\text{IDF}(q_i,C)=\ln \left(\frac{|C|-\text{DF}(q_i,C)+0.5}{\text{DF}(q_i,C)+0.5}+1\right)$$
其中文档频率$\text{DF}(q_i,C)$是$C$中包含$q_i$的文档数。尽管$B(Q,D)$依赖于查询(query)，而查询仅在检索期间提供，下面会展示如何重构等式，以便在索引时即时计算$\text{TF}$和$\text{IDF}$。

即时索引评分 现在考虑词表$V$中的所有标记，记作$t\in V$。我们可以重构$S(t,D)$为：
$$S(t,D)=\text{TF}(t,D)\cdot \text{IDF}(t,C)\frac{1}{\mathcal{D}}$$
当$t$是文档$D$中不存在的标记时，$\text{TF}(t,D)=0$，这也导致$S(t,D)=0$。这意味着，对于词表$V$中的大多数标记，我们可以简单地将相关性评分设置为0，仅计算实际出现在文档$D$中的$t$的值。这个计算可以在索引过程中完成，从而避免在查询时计算$S(q_i,D)$。

分配查询评分

考虑形状为$|V|\times |C|$的稀疏矩阵，可以使用查询标记选择相关的行，从而得到一个形状为$|Q|\times |C|$的矩阵，然后可以在列维度上进行求和，最终得到一个单一的$|C|$维向量(表示每个文档对查询的评分)。

高效矩阵稀疏

采用压缩稀疏列(Compressed Sparse Column, CSC)格式实现稀疏矩阵(使用scipy.sparse.csc_matrix)，这在坐标格式与CSC格式之间提供了高效的转换。由于我们在列维度上进行切片和求和，这一实现是稀疏矩阵实现中的最佳选择。在实践中，我们直接使用Numpy数组来复制稀疏操作。

分词

为了拆分文本，使用与Scikit-Learn为其自己的标记器所用的相同正则表达式模式，模式为r"(?u)\b\w\w+\b"。该模式便捷地解析UTF-8中的单词(涵盖多种语言)，其中\b​处理单词边界。然后，如果需要词干提取，我们可以对词汇表中的所有单词进行词干提取，以便查找集合中每个单词的词干版本。最后，我们构建一个字典，将每个唯一的(词干)单词映射到一个整数索引，以便将标记转换为相应的索引，从而显著减少内存使用并使其能够用于切片Scipy矩阵和Numpy数组。

Top-k 选择

在计算完集合中所有文档的评分后，我们可以通过选择前 k 个最相关的元素来完成搜索过程。一种简单的方法是对评分向量进行排序，并选择最后 k 个元素；而作者采用的是对数组的划分，仅选择最后 k 个文档(无序)。使用像 Quickselect这样的算法，可以在平均时间复杂度为 $O(n)$的情况下完成这一操作，其中 n 是集合中的文档数量，而排序需要 $O(n\log n)$。如果用户希望按顺序接收前 k 个结果，排序划分后的文档将额外消耗 $O(klogk)$ 的时间复杂度，这在假设 $k\ll n$ 的情况下是可以忽略不计的。

在实践中，BM25S 允许使用两种实现：一种基于 numpy，利用 np.argpartition，另一种基于 jax，依赖于 XLA 的 top-k 实现。Numpy 的 argpartition 使用了内省选择算法，该算法修改了 quickselect 算法，以确保最坏情况下的性能保持在 $O(n)$ 内。实际上观察到 JAX 的实现上表现更佳。

多线程

通过池化执行器实现可选的多线程功能，以在检索过程中进一步加速。

BM25 的替代实现

上述内容描述了如何为 BM25 的一种变体(Lucene)实现 BM25S。然而，可以很容易地将 BM25S 方法扩展到许多 BM25 的变体。

2.1 基于未出现调整扩展稀疏性

对于 BM25L、BM25+，当 $\text{TF}(t,D)=0$时，$S(t,D)$ 的值不会为零。将这个值记作标量 $S^{\theta }(t)$，表示当 $t$ 不出现在文档 $D$ 中时的得分。

显然，构建一个 $|V|\times |C|$ 的稠密矩阵会消耗过多内存。相反，我们仍然可以通过从得分矩阵中每个标记 $t$和文档 $D$ 中减去 $S^{\theta }(t)$ 来实现稀疏性(因为词汇中的大多数标记 $t$不会出现在任何给定文档 $D$ 中，它们在得分矩阵中的值将为 0)。然后，在检索过程中，我们只需计算每个查询 $q_i\in Q$ 的 $S^{\theta }(q_i)$，并对其进行求和，以获取一个可以加到最终得分上的标量。更正式地，对于一个空文档 $\varnothing$，定义 $S^{\theta }(t)=S(t,\varnothing )$ 为标记 $t$ 的非出现得分。然后，差分 $S^{∆}(t,D)$​ 定义为：
$$S^{∆}(t,D)=S(t,D)-S^{\theta }(t)$$
因此，我们重构BM25(B)评分为：
$$\begin{array}{rl}B(Q,D)& =\sum _{i=1}^{|Q|}S(q_i,D)\\ & =\sum _{i=1}^{|Q|}\left(S(q_i,D)-S^{\theta }(q_i)+S^{\theta }(q_i)\right)\\ & =\sum _{i=1}^{|Q|}\left(S^{\Delta }(q_i,D)+S^{\theta }(q_i)\right)\\ & =\sum _{i=1}^{|Q|}{S}^{\Delta }(q_i,D)+\sum _{i=1}^{|Q|}{S}^{\theta }(q_i)\end{array}$$
其中${\sum }_{i=1}^{|Q|}{S}^{\Delta }(q_i,D)$ 可以使用差分稀疏得分矩阵高效计算在 scipy 中实现。此外，${\sum }_{i=1}^{|Q|}{S}^{\theta }(q_i)$​只需要对查询 Q 计算一次，随后可以应用于每个检索到的文档以获得确切的得分。

3. 基准测试

吞吐量

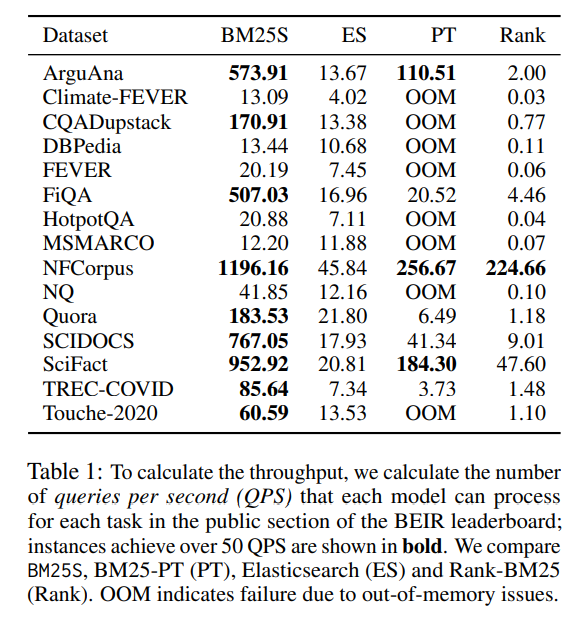
为了进行基准测试，使用 BEIR 基准中公开可用的数据集。表 1 中的结果显示，BM25S 的速度显著快于 Rank-BM25。

分词的影响

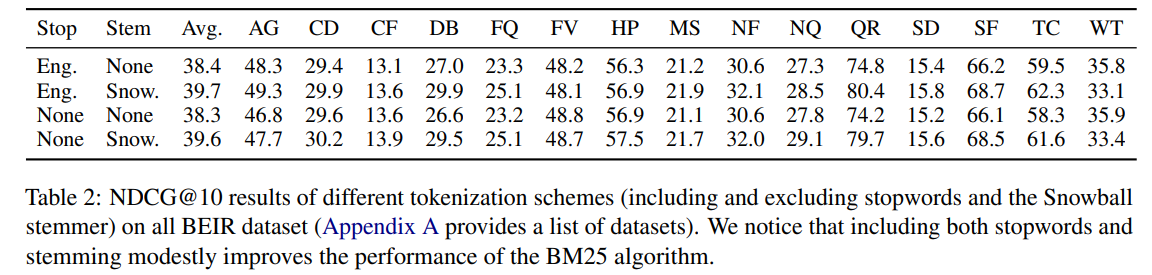
进一步通过比较 BM25S Lucene($k_1=1.5,b=0.75$​)的表现，检查分词对每个模型的影响，分别为 (1) 不进行词干提取，(2) 不去除停用词，(3) 两者都不去除，以及 (4) 都去除。总体而言，添加词干提取器平均上会提高得分，而停用词的影响较小。然而，在个别情况下，停用词可能会产生更大的影响。

比较模型变体

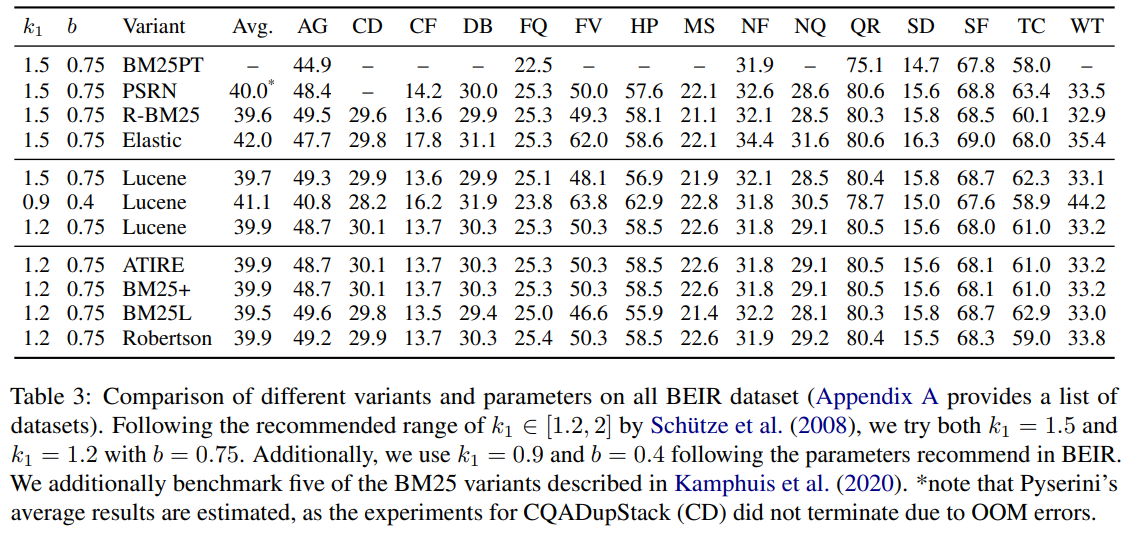
在表 3 中，比较了多个实现变体。大多数实现的平均得分在 39.7 到 40 之间，只有 Elastic 实现了稍高的得分。这种差异可以归因于分词方案的不同。

4. 结论

作者提供了一种新颖的计算 BM25 分数的方法，称为 BM25S，该方法不仅提供开箱即用的快速分词和高效的前 K 个选择，还最小化了依赖关系，使其能够直接在 Python 中使用。通过最小化依赖关系，BM25S 成为在存储可能受到限制的场景(例如边缘部署)中的良好选择。

实战

首先安装相相关库：

pip install bm25s
1

该项目默认只支持英文系列的语言，但我们可以简单修改，加入结巴分词让它支持中文：

from bm25s.tokenization import Tokenized
import jieba
from typing import List, Union
from tqdm.auto import tqdm


def tokenize(
    texts,
    return_ids: bool = True,
    show_progress: bool = True,
    leave: bool = False,
) -> Union[List[List[str]], Tokenized]:
    if isinstance(texts, str):
        texts = [texts]

    corpus_ids = []
    token_to_index = {}

    for text in tqdm(
        texts, desc="Split strings", leave=leave, disable=not show_progress
    ):

        splitted = jieba.lcut(text)
        doc_ids = []

        for token in splitted:
            if token not in token_to_index:
                token_to_index[token] = len(token_to_index)

            token_id = token_to_index[token]
            doc_ids.append(token_id)

        corpus_ids.append(doc_ids)

    # Create a list of unique tokens that we will use to create the vocabulary
    unique_tokens = list(token_to_index.keys())

    vocab_dict = token_to_index

    # Return the tokenized IDs and the vocab dictionary or the tokenized strings
    if return_ids:
        return Tokenized(ids=corpus_ids, vocab=vocab_dict)

    else:
        # We need a reverse dictionary to convert the token IDs back to tokens
        reverse_dict = unique_tokens
        # We convert the token IDs back to tokens in-place
        for i, token_ids in enumerate(
            tqdm(
                corpus_ids,
                desc="Reconstructing token strings",
                leave=leave,
                disable=not show_progress,
            )
        ):
            corpus_ids[i] = [reverse_dict[token_id] for token_id in token_ids]

        return corpus_ids
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

然后通过bm25s.tokenize = tokenize替换默认，下面参考官网给出一个简单的例子：

import bm25s

bm25s.tokenize = tokenize

# Create your corpus here
corpus = [
    "今天天气晴朗，我的心情美美哒",
    "小明和小红一起上学",
    "我们来试一试吧",
    "我们一起学猫叫",
    "我和Faker五五开",
    "明天预计下雨，不能出去玩了",
]

# corpus = load_corpus("data")

# Tokenize the corpus and index it
corpus_tokens = bm25s.tokenize(corpus)
print(corpus_tokens)

retriever = bm25s.BM25(corpus=corpus)
retriever.index(corpus_tokens)

query = "明天天气怎么样"
query_tokens = bm25s.tokenize(query)
docs, scores = retriever.retrieve(query_tokens, k=3)
print(f"Best result (score: {scores[0, 0]:.2f}): {docs[0, 0]}")
print(docs, scores)

# Happy with your index? Save it for later...
retriever.save("bm25s_index_animals")

# ...and load it when needed
ret_loaded = bm25s.BM25.load("bm25s_index_animals", load_corpus=True)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

Tokenized(ids=[[0, 1, 2, 3, 4, 5, 6, 7], [8, 9, 10, 11], [12, 13, 14, 15], [12, 10, 16, 17], [3, 18, 19, 20], [21, 22, 23, 2, 24, 25, 26]], vocab={'今天': 0, '天气晴朗': 1, '，': 2, '我': 3, '的': 4, '心情': 5, '美美': 6, '哒': 7, '小明': 8, '和小红': 9, '一起': 10, '上学': 11, '我们': 12, '来': 13, '试一试': 14, '吧': 15, '学': 16, '猫叫': 17, '和': 18, 'Faker': 19, '五五开': 20, '明天': 21, '预计': 22, '下雨': 23, '不能': 24, '出去玩': 25, '了': 26})

Best result (score: 0.53): 明天预计下雨，不能出去玩了
[['明天预计下雨，不能出去玩了' '今天天气晴朗，我的心情美美哒' '小明和小红一起上学']] [[0.5313357 0.        0.       ]]
1
2
3
4