OpenCV-Python快速入门（九）：直方图_python opencv 直方图

前言

• 本文是个人快速入门OpenCV-Python的电子笔记，由于水平有限，难免出现错漏，敬请批评改正。
• 更多精彩内容，可点击进入
  OpenCV-Python快速入门专栏或我的个人主页查看

前提条件

• 熟悉Python

实验环境

• Python 3.x （面向对象的高级语言）
• OpenCV 4.0（python第三方库）pip3 install opencv-python

直方图

• 直方图是图像处理过程中的一种非常重要的分析工具。直方图从图像内部灰度级的角度对图像进行表述，包含十分丰富而重要的信息。从直方图的角度对图像进行处理，可以达到增强 图像显示效果的目的。
• 从统计的角度讲，直方图是图像内灰度值的统计特性与图像灰度值之间的函数，直方图统计图像内各个灰度级出现的次数。从直方图的图形上观察，横坐标是图像中各像素点的灰度级，纵坐标是具有该灰度级（像素值）的像素个数。
• 在实际处理中，图像直方图的 x 轴区间一般是[0, 255]，对应的是8 位位图的256 个灰度级；y 轴对应的是具有相应灰度级的像素点的个数。
• 虽然 8 位的图像都具有 256 个灰度级（每一个像素可以有 256 个灰度值），但是属于不同灰度级的像素数量是很不一样的。
• 有时为了便于表示，也会采用归一化直方图。在归一化直方图中，x 轴仍然表示灰度级；y轴不再表示灰度级出现的次数，而是灰度级出现的频率。
• $灰度级出现的频率=\frac{灰度级出现的次数}{总像素数}$
• 在 OpenCV 的官网上，特别提出了要注意三个概念：DIMS、BINS、RANGE。
  • DIMS：表示在绘制直方图时，收集的参数的数量。一般情况下，直方图中收集的数据只有一种，就是灰度级。因此，该值为 1。
  • RANGE：表示要统计的灰度级范围，一般为[0, 255]。0 对应的是黑色，255 对应的是白色。
  • BINS：参数子集的数目。在处理数据的过程中，有时需要将众多的数据划分为若干个组，再进行分析。

绘制直方图

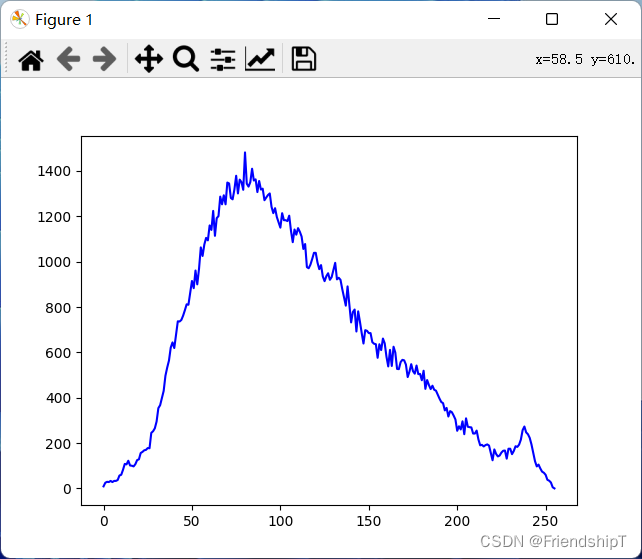
OpenCV 提供了函数 cv2.calcHist()用来计算图像的统计直方图，该函数能统计各个灰度级 的像素点个数。利用 matplotlib.pyplot 模块中的 plot()函数，可以将函数 cv2.calcHist()的统计结果绘制成直方图。

import cv2
import numpy as np
import matplotlib.pyplot as plt
img1=cv2.imread("1.jpg",0)
img1_resize=cv2.resize(img1,(400,400))
'''
hist = cv2.calcHist( images, channels, mask, histSize, ranges, accumulate )
参数说明：
    hist：返回的统计直方图，是一个一维数组，数组内的元素是各个灰度级的像素个数。
    images：原始图像，该图像需要使用“[ ]”括起来。
    channels：指定通道编号。通道编号需要用“[ ]”括起来，
        如果输入图像是单通道灰度图像，该参数的值就是[0]。
        对于彩色图像，它的值可以是[0]、[1]、[2]，分别对应通道B、G、R。
    mask：掩模图像。当统计整幅图像的直方图时，将这个值设为 None。
        当统计图像某一部分的直方图时，需要用到掩模图像。
    histSize：BINS 的值，该值需要用“[ ]”括起来。
        例如，BINS 的值是 256，需要使用“[256]”作为此参数值。
    ranges：即像素值范围。例如，8 位灰度图像的像素值范围是[0, 255]。
    accumulate：累计（累积、叠加）标识，默认值为 False。
        如果被设置为 True，则直方图
        在开始计算时不会被清零，计算的是多个直方图的累积结果，
        用于对一组图像计算直方图。
        该参数允许从多个对象中计算单个直方图，或者实时更新直方图。
        该参数是可选的，一般情况下不需要设置。
'''
hist = cv2.calcHist([img1_resize],[0],None,[256],[0,255])
plt.plot(hist,color='b')
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

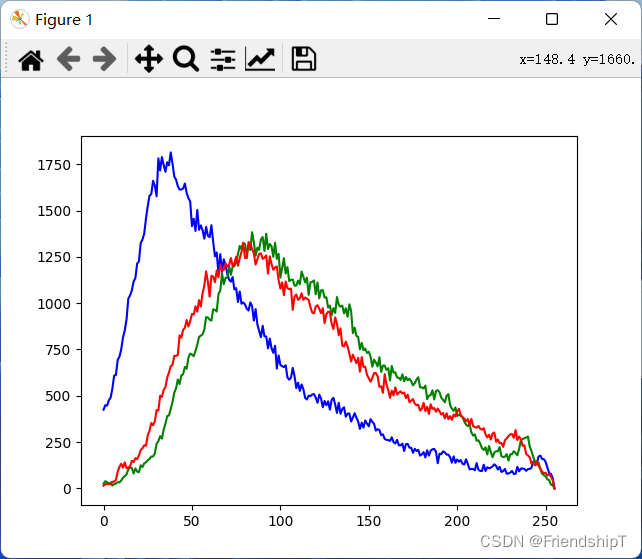
import cv2
import numpy as np
import matplotlib.pyplot as plt
img1=cv2.imread("1.jpg")
img1_resize=cv2.resize(img1,(400,400))
'''
hist = cv2.calcHist( images, channels, mask, histSize, ranges, accumulate )
参数说明：
    hist：返回的统计直方图，是一个一维数组，数组内的元素是各个灰度级的像素个数。
    images：原始图像，该图像需要使用“[ ]”括起来。
    channels：指定通道编号。通道编号需要用“[ ]”括起来，
        如果输入图像是单通道灰度图像，该参数的值就是[0]。
        对于彩色图像，它的值可以是[0]、[1]、[2]，分别对应通道B、G、R。
    mask：掩模图像。当统计整幅图像的直方图时，将这个值设为 None。
        当统计图像某一部分的直方图时，需要用到掩模图像。
    histSize：BINS 的值，该值需要用“[ ]”括起来。
        例如，BINS 的值是 256，需要使用“[256]”作为此参数值。
    ranges：即像素值范围。例如，8 位灰度图像的像素值范围是[0, 255]。
    accumulate：累计（累积、叠加）标识，默认值为 False。
        如果被设置为 True，则直方图
        在开始计算时不会被清零，计算的是多个直方图的累积结果，
        用于对一组图像计算直方图。
        该参数允许从多个对象中计算单个直方图，或者实时更新直方图。
        该参数是可选的，一般情况下不需要设置。
'''
histb = cv2.calcHist([img1_resize],[0],None,[256],[0,255])
histg = cv2.calcHist([img1_resize],[1],None,[256],[0,255])
histr = cv2.calcHist([img1_resize],[2],None,[256],[0,255])
plt.plot(histb,color='b')
plt.plot(histg,color='g')
plt.plot(histr,color='r')
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

直方图均衡化

• 如果一幅图像拥有全部可能的灰度级，并且像素值的灰度均匀分布，那么这幅图像就具有高对比度和多变的灰度色调，灰度级丰富且覆盖范围较大。在外观上，这样的图像具有更丰富的色彩，不会过暗或过亮。
• 直方图均衡化的主要目的是将原始图像的灰度级均匀地映射到整个灰度级范围内，得到一个灰度级分布均匀的图像。这种均衡化，既实现了灰度值统计上的概率均衡，也实现了人类视觉系统（Human Visual System，HVS）上的视觉均衡。
• 直方图均衡化的算法主要包括两个步骤：
  （1）计算累计直方图。
  （2）对累计直方图进行区间转换
  在此基础上，再利用人眼视觉达到直方图均衡化的目的。
• 例如，一张3×3图像img，它是一幅 3 位的位图，即共有 4=$2^2$个灰度级，具有9像素：$$\left[\begin{array}{ccc}1& 1& 3\\ 2& 3& 2\\ 2& 1& 0\end{array}\right]$$
• 图像img的统计直方图，如下表所示。

灰度级(像素值)	0	1	2	3
像素个数	1	3	3	2

• 计算归一化统计直方图，计算方式是计算每个像素在图像内出现的概率。$出现概率=\frac{出现次数}{像素总数}$，用每个灰度级的像素个数除以总的像素个数（9），就得到归一化统计直方图，如下表所示。

灰度级(像素值)	0	1	2	3
概率	$\frac{1}{9}$	$\frac{1}{3}$	$\frac{1}{3}$	$\frac{2}{9}$

• 计算累计统计直方图，即计算所有灰度级的累计概率，如下表所示。

灰度级(像素值)	0	1	2	3
累计概率	$\frac{1}{9}$	$\frac{1}{9}+\frac{1}{3}=\frac{4}{9}$	$\frac{4}{9}+\frac{1}{3}=\frac{7}{9}$	$\frac{7}{9}+\frac{2}{9}=1$

• 计算均衡化后的直方图，常见的方式有两种，一种是在原有范围内实现直方图均衡化时，用当前灰度级的累计概率乘以当前灰度级的最大值，另一种是在更广泛的范围内实现直方图均衡化时，用当前灰度级的累计概率乘以更广泛范围灰度级的最大值，得到新的灰度级，并作为均衡化的结果。如下表所示。

灰度级(像素值)	0	1	2	3
像素个数	1	3	3	2
累计概率	$\frac{1}{9}$	$\frac{4}{9}$	$\frac{7}{9}$	$1$
原始范围均衡化（新的灰度级）	$3\times \frac{1}{9}\approx 0$	$3\times \frac{4}{9}\approx 1$	$3\times \frac{7}{9}\approx 2$	$3\times 1=3$
[0,255]范围均衡化（新的灰度级）	$255\times \frac{1}{9}\approx 28$	$3\times \frac{4}{9}\approx 113$	$255\times \frac{7}{9}\approx 198$	$255\times 1=255$

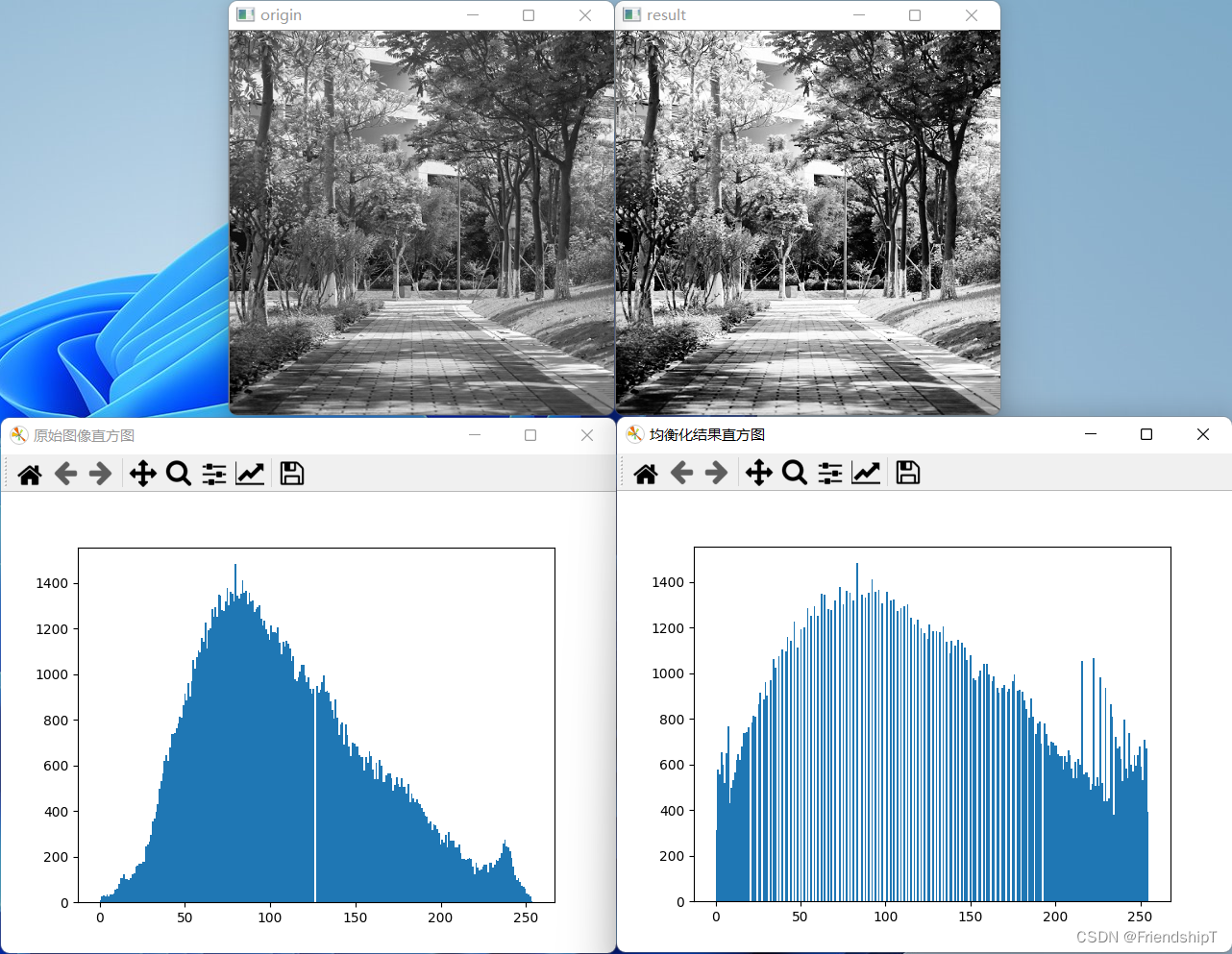
import cv2
import numpy as np
import matplotlib.pyplot as plt
img1=cv2.imread("1.jpg",0)
img1_resize=cv2.resize(img1,(400,400))
# 直方图均衡化处理dst = cv2.equalizeHist(src)
equ = cv2.equalizeHist(img1_resize)
# 显示均衡化前后的图像
cv2.imshow("origin",img1_resize)
cv2.imshow("result",equ)
'''
plt.hist(X，BINS)
参数说明：
    X：数据源，必须是一维的。图像通常是二维的，
        需要使用 ravel()函数将图像处理为一维数据源以后，再作为参数使用。
    BINS：BINS 的具体值，表示灰度级的分组情况。
    函数 ravel()的作用是将二维数组降维成一维数组
'''
# 显示均衡化前后的直方图
plt.figure("原始图像直方图") #构建窗口
plt.hist(img1_resize.ravel(),256)
plt.figure("均衡化结果直方图") #构建新窗口
plt.hist(equ.ravel(),256)
plt.show()
# 等待释放窗口
cv2.waitKey()
cv2.destroyAllWindows()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

参考文献

[1] https://opencv.org/
[2] 李立宗. OpenCV轻松入门：面向Python. 北京： 电子工业出版社，2019

• 更多精彩内容，可点击进入
  OpenCV-Python快速入门专栏或我的个人主页查看