多模态信息中的神经网络集成学习方式(个人笔记-持续更新)_lggnet: learning from local-global-graph represent

Introduction

• 目前的工作考虑多个多模态学习器的late fusion的增强，系统学习下传统的和最近的集成学习成果，尤其是对神经网络的集成学习方式，看到了一篇名为GrowNet的论文
• 本文从传统的集成学习方式展开，侧重于Boosting的集成学习方式
• 介绍了Gradient Boosting的原理和GBDT
• 介绍了GrowNet，近期的集成学习用于神经网络弱分类器论文

传统的集成学习方式分类

何为集成方法？

集成学习是一种机器学习范式。在集成学习中，我们会训练多个弱分类器解决相同的问题，并将它们结合起来以获得更好的结果。最重要的假设是：当弱模型被正确组合时，我们可以得到更精确或更鲁棒的模型。在大多数情况下，这些基本模型本身的性能并不是非常好，这要么是因为它们具有较高的方差或者偏差。

集成方法的思想是通过将这些弱学习器的偏置和/或方差结合起来，从而创建一个强学习器，从而获得更好的性能。根据弱学习器的性质，又分为同质和异质学习器。

• bagging，该方法通常考虑的是同质弱学习器，相互独立地并行学习这些弱学习器，最后通过投票、平均等方式组合多个弱学习器的预测；
  • 学习方式：对N个样本采样为$B1,B2...B_n$作为多个样本用于Bagging中弱学习器学习并将其平均，Random Forest就是其中一种；
  • 其重点在于减小方差；

---

• boosting，该方法通常考虑的也是同质弱学习器。它顺序地学习这些弱学习器（每个基础模型都依赖于前面的模型），并按照某种确定性的策略将它们组合起来。
  • 图下图所示，顺序地学习全部数据并创建新分类器用来对上一个分类器的不佳数据进行重点学习，主要在于降低偏差；
  • 每一次建立模型是在之前建立模型损失函数的梯度下降方向；
    

---

• stacking，该方法通常考虑的是异质弱学习器，并行地学习它们，并用一个名为元模型的学习器将它们组合起来，根据不同弱模型的预测结果输出一个最终的预测结果。
  • 例如，对于分类问题来说，我们可以选择 KNN 分类器、logistic 回归和SVM 作为弱学习器，并决定学习神经网络作为元模型。然后，神经网络将会把三个弱学习器的输出作为输入，并返回基于该输入的最终预测。

---

梯度提升分类器Gradient Boosting

原理简介

先介绍AdaBoost

• 类似于Gradient Boosting，AdaBoost也是一种提升弱分类器的集成学习方式：
  

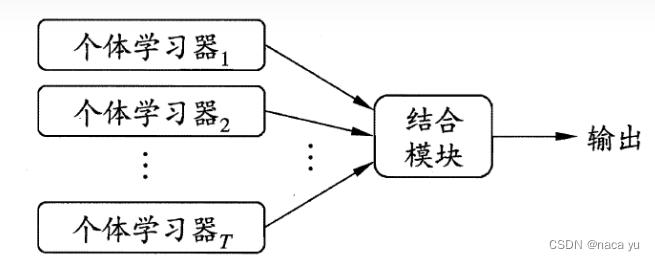
1. AdaBoost将带有相同初始权重$W_1$的数据$X_1$送入初始学习器$M_1$学习，将分类错误的样本重新分配权重$W_2$；
2. 将带有$W_2$权重的样本$X_2$送入学习器2并重复上述1步骤；
3. 得到满足的结果后，一共有T个不同的学习器；

• 送入新数据时，结合T个学习器的预测作为输出。

---

由AdaBoost到Gradient Boosting

• AdaBoost，我认为其本质是一种以“预测差值”为优化目标的学习方式，但是这类差值是人为定义的“初级差值”，为什么说是初级，因为其偏差是启发式地引入样本权重，在Gradient Boosting中，其偏差类似梯度下降，是以一种更高级的偏差方式存在；它每一次建立模型是在之前建立模型损失函数的梯度下降方向相较于AdaBoost通过调整数据权重的方式不同。
• 经典的AdaBoost算法只能处理采用指数损失函数的二分类学习任务，而梯度提升方法通过设置不同的损失函数（可微分）可以处理各类学习任务（多分类、回归、Ranking等），应用范围大大扩展；
• AdaBoost算法对异常点（outlier）比较敏感（因为其专注于针对困难样本学习），而梯度提升算法通过引入bagging思想、加入正则项等方法能够有效地抵御训练数据中的噪音，具有更好的健壮性；

• 梯度提升算法，类比于梯度下降参数更新，将优化目标从模型参数到模型函数（可以类比泛函空间，此时的泛函就是L(y,F(x))），此时求解最优的模型（函数），就要求解使Loss函数最小时的f(x)。同时，可以从迭代函数来看，Gradient Boosting生成新的模型，而不是取代之前的弱分类器。

• 其中，设最优函数为：$F_0(x)=f_0(x)$为初始的模型函数，我们的优化目标为$F^{\ast }(x)$。在泛函上的定义上来说，$f(x)$为总量，$F(x)$为泛函，我们的优化过程就是不断地求出泛函的梯度，使其向$F^{\ast }(x)$转化，即求出极小值，这个极小值就是$f^{\ast }(x)$，最优的模型函数。

---

引入梯度提升树(GBDT)

• 基于上述的梯度提升优化原理，目前基于此的一种算法GBDT为竞赛中常用的一种分类器，即每次根据上一次预测的负梯度方向优化生成新的树；
  
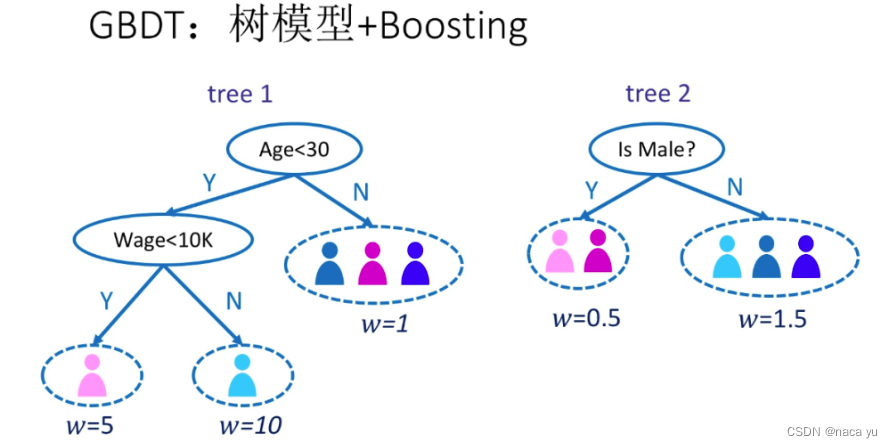
• 以上是一个基本的决策树模型；
• 梯度提升树以Classification And Regression Trees(CART)这种类型的树为主；

GBDT的目标函数

关于GBDT，建议看这篇文章：https://www.zybuluo.com/yxd/note/611571

---

GBDT算法可以看成是由K棵树组成的加法模型：
$$\widehat{y_i}={\Sigma }_{k=1}^K{f}_k(x_i),f_k\in F\text{\hspace{1em}(0)}$$
其中每一个预测值都是来自于K棵树的叠加：

• F为决策树所有可能的函数空间，考虑不带有正则项下的目标函数；
• ${\hat{y}}_i$为对于某个输入样本xi的预测结果；
• K决策树数量；

下面是我们的优化目标函数：

$$Obj={\Sigma }_{i=1}^{n}Loss(y_i,\widehat{y_i})\text{\hspace{1em}(1)}$$
其中，我们的目标就是在n个样本的总体预测损失，这里我们省去了正则项：

• $y_i$为样本xi的ground truth；
• Loss为损失函数；

因为学习的是加法模型，如果能够从前往后，每一步只学习一个基函数及其系数（结构），逐步逼近优化目标函数，那么就可以简化复杂度。这一学习过程称之为Boosting。具体地，我们从一个常量预测开始，每次学习一个新的函数，过程如下
y ^ i 0 = 0 y ^ i 1 = f 1 ( x i ) = y ^ i 0 + f 1 ( x i ) y ^ i 2 = f 1 ( x i ) + f 2 ( x i ) = y ^ i 1 + f 2 ( x i ) ⋯ y ^ i t = ∑ k = 1 t f k ( x i ) = y ^ i t − 1 + f t ( x i ) (2)

$$\begin{aligned} \hat{y}_i^0 &= 0 \\ \hat{y}_i^1 &= f_1(x_i) = \hat{y}_i^0 + f_1(x_i) \\ \hat{y}_i^2 &= f_1(x_i) + f_2(x_i) = \hat{y}_i^1 + f_2(x_i) \\ & \cdots \\ \hat{y}_i^t &= \sum_{k=1}^t f_k(x_i) = \hat{y}_i^{t-1} + f_t(x_i) \\ \tag{2} \end{aligned}$$ y^​i0​y^​i1​y^​i2​y^​it​​=0=f1​(xi​)=y^​i0​+f1​(xi​)=f1​(xi​)+f2​(xi​)=y^​i1​+f2​(xi​)⋯=k=1∑t​fk​(xi​)=y^​it−1​+ft​(xi​)​(2)
如何决定我们加入的函数$f$，也就是如何决定下一颗树的参数呢？
那就要通过优化当前的目标函数，假设我们现在到了第$t$棵树需要生成，我们的优化函数为，通过最小化这个函数，我们得到下一棵树的参数：
$$\begin{array}{rl}Ob{j}^{(t)}& =\sum _{i=1}^{n}l(y_i,{\hat{y}}_i^t)\\ & =\sum _{i=1}^{n}l\left(y_i,{\hat{y}}_i^{t-1}+f_t(x_i)\right)+constant\end{array}\text{\hspace{1em}(3)}$$
如果我们将平方损失函数MSE作为标准，那么（3）就变成：
$$\begin{array}{rl}Ob{j}^{(t)}& =\sum _{i=1}^n{\left(y_i-({\hat{y}}_i^{t-1}+f_t(x_i))\right)}^2+constant\\ & =\sum _{i=1}^n\left[2({\hat{y}}_i^{t-1}-y_i)f_t(x_i)+f_t(x_i{)}^2\right]+constant\end{array}\text{\hspace{1em}(4)}$$
根据泰勒公式：

我们将（4）式进行二阶泰勒展开变成（去掉常量，因为常量在梯度优化中不起作用）：
$$Ob{j}^{(t)}\approx \sum _{i=1}^n\left[l(y_i,{\hat{y}}_i^{t-1})+g_i{f}_t(x_i)+\frac{1}{2}{h}_i{f}_t^2(x_i)\right]\text{\hspace{1em}(5)}$$
其中：

• gi为损失函数的一阶导数
• hi为损失函数的二阶导数
• $f_t(x_i)$为$\Delta x$
• ${\hat{y}}_i^{t-1}$为x

我们只需要最小化公式（5），就可以得到我们的目标函数$f_t(x)$。

---

GBDT的子树

• 上述是我们需要的下一课子树的目标函数，但是我们需要确定子树内部的节点，将叶子节点的公式带入式（5）得：
  O b j ( t ) ≈ ∑ i = 1 n [ g i f t ( x i ) + 1 2 h i f t 2 ( x i ) ] + Ω ( f t ) = ∑ i = 1 n [ g i w q ( x i ) + 1 2 h i w q ( x i ) 2 ] + γ T + 1 2 λ ∑ j = 1 T w j 2 = ∑ j = 1 T [ ( ∑ i ∈ I j g i ) w j + 1 2 ( ∑ i ∈ I j h i + λ ) w j 2 ] + γ T (6)

  $$\begin{aligned} Obj^{(t)} &\approx \sum_{i=1}^n \left[ g_if_t(x_i) + \frac12h_if_t^2(x_i) \right] + \Omega(f_t) \\ &= \sum_{i=1}^n \left[ g_iw_{q(x_i)} + \frac12h_iw_{q(x_i)}^2 \right] + \gamma T + \frac12 \lambda \sum_{j=1}^T w_j^2 \\ &= \sum_{j=1}^T \left[(\sum_{i \in I_j}g_i)w_j + \frac12(\sum_{i \in I_j}h_i + \lambda)w_j^2 \right] + \gamma T \end{aligned}$$ \tag 6 Obj(t)​≈i=1∑n​[gi​ft​(xi​)+21​hi​ft2​(xi​)]+Ω(ft​)=i=1∑n​[gi​wq(xi​)​+21​hi​wq(xi​)2​]+γT+21​λj=1∑T​wj2​=j=1∑T​⎣⎡​(i∈Ij​∑​gi​)wj​+21​(i∈Ij​∑​hi​+λ)wj2​⎦⎤​+γT​(6)
  其中：

• T为叶子节点个数，$q_i(x)$为特征向量x到子节点索引 {1,2…T} 映射， q : R d → { 1 , 2 , ⋯   , T } q:R^d \to \{1,2,\cdots,T\} q:Rd→{1,2,⋯,T}

• $\omega \in R^T$，其中ω是叶子节点的向量集合，特征向量：$x(R^d)\to q(R^1)\to \omega (R^T)$

• $\Omega (f_t)=\gamma T+\frac{1}{2}\lambda {\sum }_{j=1}^T{w}_j^2$为第t个子树的正则参数，包括对于叶子节点的数量和叶子节点的参数；

$$Ob{j}^{(t)}=\sum _{j=1}^T\left[G_i{w}_j+\frac{1}{2}(H_i+\lambda )w_j^2\right]+\gamma T\text{\hspace{1em}(7)}$$
将上述式子对ω*求导得函数的最小值：
$$w_j^{\ast }=-\frac{G_j}{H_j+\lambda }\text{\hspace{1em}(8)}$$
将$\omega j^{\ast }$其待入目标函数得：
$$Obj=-\frac{1}{2}\sum _{j=1}^T\frac{G_j^2}{H_j+\lambda }+\gamma T\text{\hspace{1em}(9)}$$

• 上面的（9）式的大小作为衡量标准确定某个树结构是否最优

所以，用语言描述确定某个最佳子树的整个过程为：

1. 枚举所有可能的树结构$q_i$
2. 用等式(7)为每个计算其对应的分数，分数越小说明对应的树结构越好
3. 根据上一步的结果，找到最佳的树结构，用等式(8)为树的每个叶子节点计算预测值

总结

整体来说：
4. 算法每次迭代生成一颗新的决策树
5. 在每次迭代开始之前，计算损失函数在每个训练样本点的一阶导数和二阶导数
6. 通过贪心策略生成新的决策树，通过等式(8)计算每个叶节点对应的预测值
7. 把新生成的决策树添加到模型中；

GrowNet

参考文章

https://blog.csdn.net/u9Oo9xkM169LeLDR84/article/details/
https://zhuanlan.zhihu.com/p/337413526
https://baijiahao.baidu.com/s?id=1633580172255481867&wfr=spider&for=pc
https://zhuanlan.zhihu.com/p/41809927
http://t.csdn.cn/kIMHZ
https://www.zybuluo.com/yxd/note/611571